背景

​ 函数估计(Function Estimation/Approximation)是对函数空间(Function Space)进行数值优化，而不是对参数空间(Paramter Space)进行优化。这篇论文(见参考)提出的Gradient Boosting Decision Tree（GBDT）算法将stagewise additive expansions(分步加和扩展)和steepest-descent minimization(最速下降极小化，也就是梯度下降法)结合起来实现对函数空间的数值优化，可以适用于regression和classification问题，具有完整性好，鲁棒性高，解释性好等优点。

动因

　　为了理解作者的动因，我们首先从我们熟悉的函数最小值优化问题谈起：

　　对于该优化问题，可以使用Steepest Gradient Descent，梯度下降法进行求解。这个算法大致过程如下：

• 给定一个起始点$x_0$
• 对$i=1,2,...,n$分别作如下迭代：
• $x_i = x_{i-1} + \beta_{i}*g_{i}$, 其中$g_{i}=-\frac{\partial f}{\partial x}|_{x=x_{i-1}}$表示$f$在$x_{i-1}$上的负梯度值，$\beta_{i}$是步长，是通过在$g_i$方向线性搜索来动态调整的。
• 一直到$|g_{i}|$足够小，或者$|x_i-x_{i-1}|$足够小，即函数收敛。

　　以上过程就是梯度下降法，可以理解为整个过程就是小步走，每小步都往函数值下降最快的方向走。这样的寻优过程得到的结果可以表示为加和形式，即：

　　我们可以从上面得到启发，这样的过程是否可以推广至函数空间求函数估计问题？求解函数估计问题本身也是一个寻优的过程，只不过我们寻找的结果是最优函数估计，而不是最优点估计。优化的目标通常通过最小化损失函数来定义：

　　类似上面的梯度下降法，我们可以构造弱分类器$\{f_1,f_2,f_3...,f_m\}$,可以类比成上述的$\{x_1,x_2,x_3...,x_m\}$,每次迭代求梯度：

　　我们发现上述求解是函数对函数求梯度， 函数对函数求导很困难，我们采取另一种方法，将函数$F_{i-1}$表示成由所有样本点在该函数上的离散值构成。即：$[F_{i-1}(x_1), F_{i-1}(x_2),...,F_{i-1}(x_N)]$

　　这是一个N维向量，可以计算：

　　上式是函数对向量的求导，得到的也是一个梯度向量。这里求导过程，首先是求$F(x_k)$,即每个样本点的F函数值，然后再根据具体的损失函数，来计算损失函数对$F(x_k)$函数值的导数，而不是对$x_k$的导数。

　　但是，$\hat{g}_i(x_k), for \ k=1,2,3..,N$只是描述了 $g_i$在每个点上的值，并不足以表达$g_i$ ，也就是说只是表达了训练集，不能泛化到其它数据上。重点在于，我们可以通过函数拟合的方法从$\hat{g}_i(x_k), for \ k=1,2,3..,N$中构造出$g_i$, 这是一个我们非常熟悉的问题，例如回归曲线拟合问题。这个问题可以当作一个子问题求解，只要损失函数可导即可。这样我们就近似得到了函数对函数的求导结果。

　　上述过程归纳起来，也就是加和扩展(additive expansion)和梯度下降(steepest-descent minimization)的结合。表示成如下形式：

主要思想

​ 了解了动因之后，我们从一般化函数估计问题谈起。首先仍然从介绍函数估计开始，函数估计的目标是得到对映射函数$F^{*}(x)$(从x映射到y)的估计$\hat{F}(x)$,使得在所有训练样本$(y,x)$的联合分布上，最小化期望损失函数$L(y, F(x))$ ：

上式是求联合分布，等于对$E_y(L(y,F(x)))|x]$在x上求边缘分布。

　　我们需要在函数空间进行数值优化。在函数空间，为了表示一个函数$F(x)$,理想状况下有无数个点，我们可以使用“非参数方法”来求解上述问题，非参数方法可以理解为，我们并没有指定$F(x)$的形式，任意的$F(x)$都有可能。

　　根据前文（参见动因一节），我们需要解：

　　$f_0(x)$是初始估计，$\{f_m(x)\}_1^M$是提升估计。使用梯度下降法：

　　其中：

　　假设可以交换微分和积分的顺序，则：

　　乘子$\rho_m$沿着步长方向$g_m$进行线性搜索，$\rho_m g_m$代表步长：

　　然而我们面对的情况是只能用有限的数据集$\{y_i,x_i\}_1^N$表示x，y的联合分布的时候，上述方法就有点行不通了，因为$E_y[\dot{} | x]$ 不能被数据集上的每个点$x_i$正确估计，即使可以，也只是针对训练集，不能泛化到其它任意点$x$。

　　因此我们需要修改解的形式。可以通过限制$F(x)$为一系列带参数的函数集合 $F(x;P), P=\{P_1,P_2,...\}$是一个有限的参数集合，即首先确定了F(x)的形式，然后再在参数空间中搜索F(x)的参数值，实际上这是将函数估计问题转化成了参数估计问题。

　　本文也采用类似的思想，使用“分步加和扩展(Stagewise Additive Expansion)”求解上述函数估计目标。即，我们定义$F(x)$的形式为：

　　其中，$h(x)$可以理解为基函数,$\alpha_m$是基函数的参数。对于GBDT而言，h(x)为CART树,而$\alpha_m$对应着这棵小的CART树的结构，$\beta_m$可以看作是该树的权重。

　　则可将上述优化问题转化为：　　

　　上述问题仍然是难以求解的。难以求解的原因是，我们要一次性同时找出所有的${\{\beta'_m,\alpha'_m\}_1^M}$（注意看min下标），也就是找出所有基函数$h(x)$和$\beta$的一个最优序列，每次有新的分类器加入，还需要调整之前的分类器。

　　一种贪心算法的思想是采用Greedy Stagewise方法，对$m=1,2,...,M$,

　　然后更新：

　　可以看出这是一种分步加和扩展的方式(注意min的下标)，即每次只训练一个弱分类器，当新分类器被加入模型的时候，不调整原来得到的分类器$F_{m-1}(x)$, 实际上是一种贪心策略。

　　对于给定的损失函数$L(y,F)$和基分类器$h(x;a)$。上式求解比较困难。假设，在$F_{m-1}(x)$确定了的前提下，并且$h(x;\alpha_m)$是$h(x;\alpha)$的X某个成员，同时也作为步长的方向，那么$\beta_mh(x;\alpha_m)$可以看作是对$F^{*}(x)$(1)的最优贪心步长(greedy step),也可以认为是(3)中的最深梯度下降步长。

　　我们构建样本函数值$F(x_i)$的负梯度如下：

　　因此N维空间$F_{m-1}(x)$上的函数负梯度可以表示为$-g_m=\{-g_m(x_i)\}_1^N$.然而这只是对训练集样本而言，不能泛化到其它样本上。也就是说，我们原本的目标是需要损失函数$L$对$F(x)$函数进行求梯度(参考动因一节)，函数对函数的梯度难以求解，现在通过所有样本在$F(x)$处的取值的梯度集合$-g_m$来近似替代$L$对$F(x)$函数的梯度。然而这里只是对训练集进行求值替代，为了能够泛化到其他数据集，我们需要根据训练集在$F(x)$取值的梯度集合拟合出$L$对$F(x)$的梯度,使得其能够泛化到其它样本上。

　　具体而言，我们需要从$h(x;\alpha)$中选择某一个$h_m\{h(x,\alpha_m)\}$，使得$\{h_m(x_i; \alpha_m)\}_1^N$和$-g_m \in R^N$最接近。这是一个典型的函数拟合问题，可以使用平方误差损失在样本上进行拟合：

　　注意上述平方误差损失只是用来拟合负梯度用的，和前面的$L$是完全不一样的两个东西。对于GBDT而言，也就是使用一棵新的回归树CART，拟合损失函数$L$对$F_{m-1}(x)$的负梯度。

　　找到负梯度拟合函数$h(x_i; \alpha_m)$后，就可以使用线性搜索方法在负梯度方向上进行搜索乘子$\rho_m$

　　然后更新模型：

　　上述实际上是在公式(5)中加入了拟合约束，即,使用$\beta h(x,\alpha)$拟合负梯度$-g_m$. 这可以将（5）中的函数最小化问题转变为(6)中的最小二乘估计问题，且该二乘估计只有一个参数，很容易求解。因此只要存在能够使用最小二乘估计求解（6）中的负梯度拟合问题的基函数$h(x;\alpha)$,那么就可以使用前向加和模型(forward stagewise additive model) 来求解复杂的损失函数优化问题。得到如下的算法：

• 1. $F_0(x) = arg \min_{\rho} \sum_{i=1}^N L(y_i, \rho)$
• 2. $For \ m=1 \ to \ M \ do:$
• 3. $\tilde{y}_i=-[\frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}]_{F(x)=F_{m-1}(x)}, i = 1, 2, 3,...,N$
• 4. $\alpha_m = arg \min_{\alpha, \beta} \sum_{i=1}^N[\tilde{y}_i - \beta h(x_i;\alpha)]^2$
• 5. $\rho_m = arg min_{\rho} \sum_{i=1}^N L(y_i, F_{m-1}(x_i) + \rho h(x_i; \alpha_m)$
• 6. $F_m(x)=F_{m-1}(x)+\rho_m h(x;\alpha_m)$

解释：

• 1.初始化，对样本点标签在损失函数上进行线性搜索得到初始分类器。
• 2.M个分类器，迭代M次：
• 3.每次求得损失函数在所有训练样本上对分类器F的梯度。
• 4.使用定制的h函数对梯度进行平方误差拟合。
• 5.在拟合得到的梯度上进行线性搜索，得到步长。
• 6.使用分步加和模型来更新分类器

　　上述第四步中实际上还可以使用其他拟合标准进行求解，最小二乘法是其中一种简单又自然的选择。

　　我们要注意上述中的$\rho_m$和（5）中的$\beta_m$是不一样的，只不过在某些特定的损失函数中，$\beta_m$的某种形式可以等价于$\rho_m$。

主要工作

　　本部分介绍作者使用不同的损失函数和基函数来运用加和模型和梯度下降策略得到的算法。

算法

Least-squares Regression

　　此时损失函数为:$L(y, F) = (y-F)^2/2$, 上述算法的第三步此时为：$\tilde{y}_i=y_i-F_{m-1}(x_i)$。则第四步直接使用$\beta h(x_i;\alpha)$拟合当前数据的残差即可，第五步线性搜索直接令$\rho_m=\beta_m$即可，其中$\beta_m$就是第四步拟合的结果。$\rho_m=\beta_m$的原因如下：

　　第一个式子是当前的优化求解目标，第二个式子是算法第四步中拟合负梯度的目标，可以看出两个优化目标完全一致，对负梯度的拟合结果得到的$\beta$，p直接就是$\rho_m$了，不需要第五步中的线性搜索。

Least absolute Deviation Regression

　　此时损失函数为 $$L(y, F) = |y-F|$$ , 则，

　　在第四步中，使用$h(x;a)$拟合$sign(residuals)$。在第五步中线性搜索为：

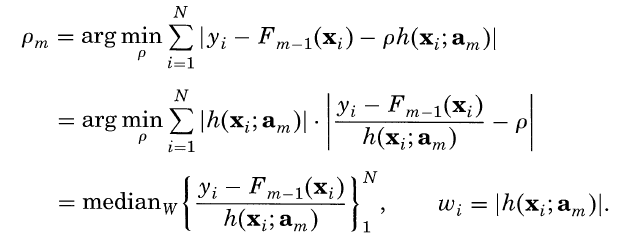
Regression trees

　　考虑基学习器为$J-terminal \ node$的回归树。

　　公式第6步更新策略如下：

　　$\{R_{jm}\}_1^J$是第m次迭代时，回归树叶节点划分出来的区域。这棵回归树被用来在第四步中拟合负梯度$\{\tilde{y}_i\}_1^N$，即每次迭代使用回归树来拟合负梯度。

　　$\{b_{jm}\}$是相应的最小二乘估计拟合负梯度得到的系数：

　　${\rho_m}$的线性搜索采用公式第五步进行求解。

　　则更新策略简写为：

　　则优化问题转化成：

　　由于回归树划分的区域是不相交的，即如果$x \in R_{jm}，则h(x)=\gamma_{j}$

Others

M-Regression、Two-class logistic regression and classification、Multiclass logistic regression and classfication

正则化

　　在训练集上训练模型来减少期望损失，通常会产生过拟合的现象。正则化通过约束训练过程来减轻过拟合。对于加和扩展模型，一种正则化思想是控制模型$\{h(x;a_m)\}_1^M$的数量$M$, 可以使用交叉验证来选择。另一种正则化思想是使用收缩因子来控制拟合过程，即学习速率。如下：

　　这两者存在一定的关系，减少学习速率意味着收敛速度降低，需要更多次迭代，则会增加模型的数量M。$v-M$实际上是一种权衡，作者通过模拟学习simulation study的过程来解释。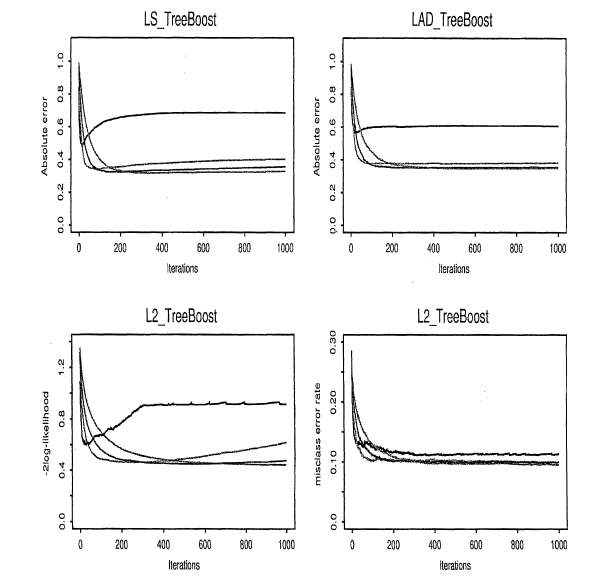

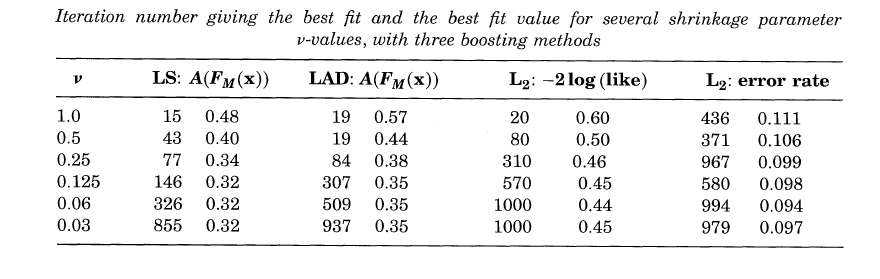
　　第一幅图使用不同的算法，每张图中不同曲线代表该算法在不同的学习速率下，预测错误率随迭代次数（M）的增加的变化情况。第二幅图同样给出了v和M的关系，可以看出，当学习速率较小时，意味着更多次迭代M，则相应的错误率也越低。

参考

Greedy Function Approximation: A Gradient Boosting Machine