分类问题
在分类问题中,你要预测的变量 y是离散的值,我们将学习一种叫做逻辑回归(Logistic Regression)的算法,这是目前最流行使用最广泛的一种学习算法。
在分类问题中,我们尝试预测的是结果是否属于某一个类(例如正确或错误)。分类问题的例子有:判断一封电子邮件是否是垃圾邮件;判断一次金融交易是否是欺诈;之前我们也谈到了肿瘤分类问题的例子,区别一个肿瘤是恶性的还是良性的。
我们从二元的分类问题开始讨论。我们将因变量(dependant variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则因变量 \(y\in{0,1}\) 其中0表示负向类,1表示正向类。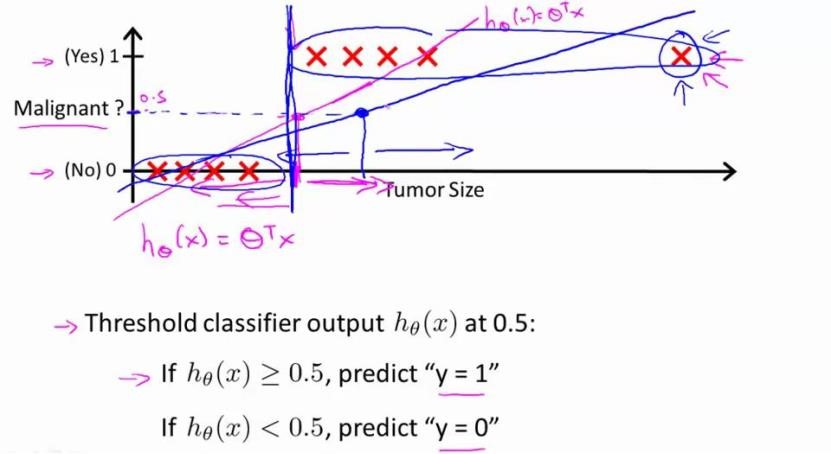
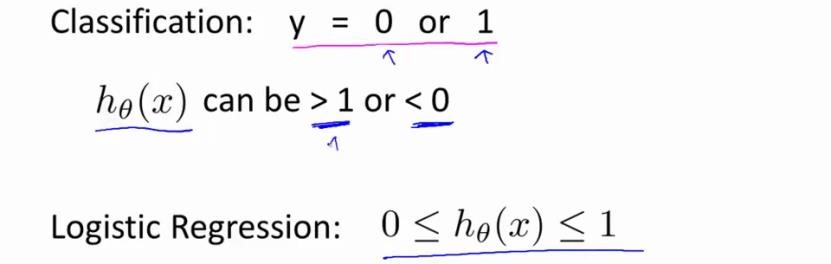
如果我们要用线性回归算法来解决一个分类问题,对于分类,y取值为 0或者1,但如果你使用的是线性回归,那么假设函数的输出值可能远大于 1,或者远小于0,即使所有训练样本的标签y都等于0或1。尽管我们知道标签应该取值0或者1,但是如果算法得到的值远大于1或者远小于0的话,就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法,这个算法的性质是:它的输出值永远在0到1之间。
顺便说一下,逻辑回归算法是分类算法,我们将它作为分类算法使用。有时候可能因为这个算法的名字中出现了“回归”使你感到困惑,但逻辑回归算法实际上是一种分类算法.
假设表示
在分类问题中,要用什么样的函数来表示我们的假设。此前我们说过,希望我们的分类器的输出值在0和1之间,因此,我们希望想出一个满足某个性质的假设函数,这个性质是它的预测值要在0和1之间。
回顾在一开始提到的乳腺癌分类问题,我们可以用线性回归的方法求出适合数据的一条直线: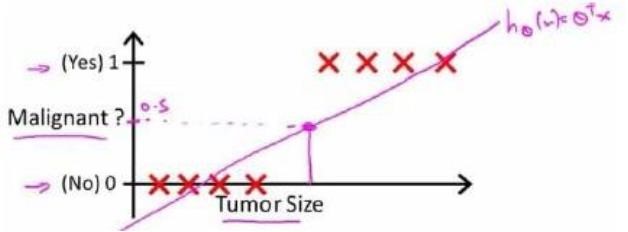
根据线性回归模型我们只能预测连续的值,然而对于分类问题,我们需要输出0或1,我们可以预测:
当\(h_θ>=0.5\)时,预测y=1。
当\(h_θ<0.5\)时,预测y=0。
对于上图所示的数据,这样的一个线性模型似乎能很好地完成分类任务。假使我们又观测到一个非常大尺寸的恶性肿瘤,将其作为实例加入到我们的训练集中来,这将使得我们获得一条新的直线。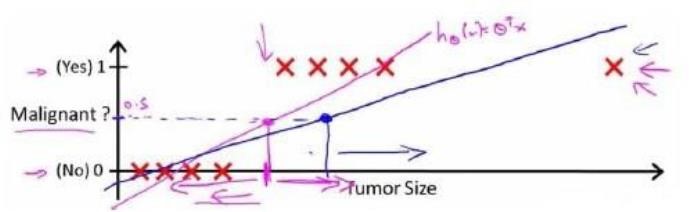
这时,再使用 0.5作为阀值来预测肿瘤是良性还是恶性便不合适了。可以看出,线性回归模型,因为其预测的值可以超越[0,1]的范围,并不适合解决这样的问题。
我们引入一个新的模型,逻辑回归,该模型的输出变量范围始终在0和 1之间。逻辑回归模型的假设是:
$$h_\theta(x)=g(\theta^TX) \\\\
其中,X代表特征向量 \\\\
g代表逻辑函数(logistic function), 也叫S形函数(Sigmoid \ function), \\\\
公式为:g(z)=\frac{1}{1+e^{-z}}
$$
该函数的图像: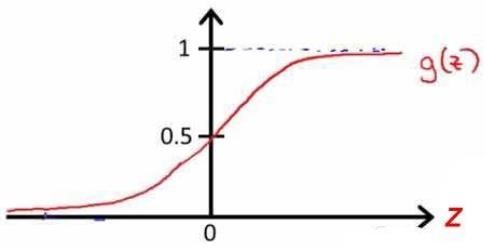
合起来,我们得到逻辑回归模型的假设:
$$h_\theta(x)=\frac{1}{1+e^{-\theta^TX}}$$
\(h_\theta(x)\)的作用是,对于给定的输入变量,根据选择的参数计算输出变量=1的可能性(estimated probablity),即:
$$h_\theta(x)=P(y=1|x;\theta)$$
例如,如果对于给定的 x,通过已经确定的参数计算得出\(h_θ(x)=0.7\),则表示有70%的几率y为正向类,相应地y为负向类的几率为1-0.7=0.3。
判定边界
现在讲下决策边界(decision boundary)的概念。这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。
在逻辑回归中,我们预测:
- 当\(h_θ\)大于等于0.5时,预测y=1;
- 当\(h_θ\)小于0.5时,预测y=0;
根据上面绘制出的S形函数图像,我们知道: - 当z=0时, g(z)=0.5;
- 当z>0时, g(z)>0.5;
- 当z<0时, g(z)<0.5.
又\(z=\theta^TX\),即:
\(\theta^TX \ge 0\),预测y=1;
\(\theta^TX < 0\),预测y=0;
现在假设我们有一个模型: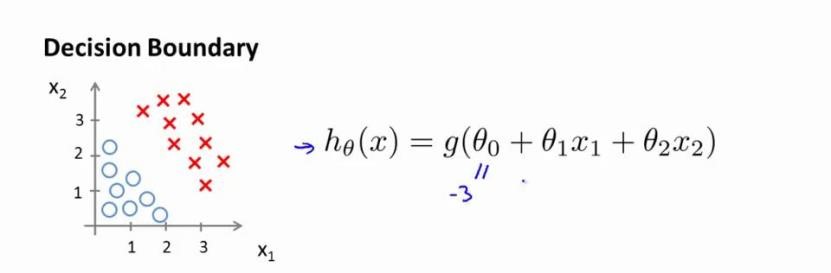
并且参数θ是向量[-3 1 1]。则当\( (-3+x_1+x_2)\ge 0\),即 \(x_1+x_2 \ge 3\)时,模型将预测y=1。
我们可以绘制直线\(x_1+x_2=3\),这条线便是我们模型的分界线,将预测为1的区域和预测为0的区域分隔开。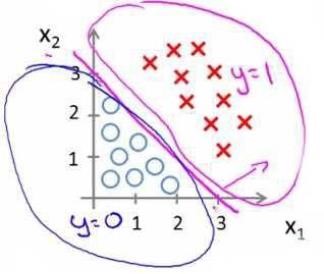
假使我们的数据呈现这样的分布情况,怎样的模型才能适合呢?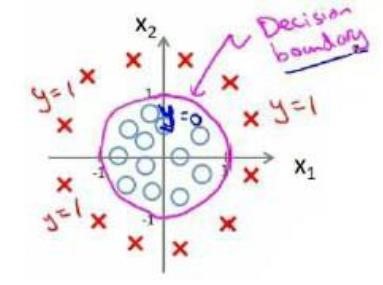
因为需要用曲线才能分隔y=0的区域和y=1的区域,我们需要二次方特征:假设参数:\(h_θ(x)=g(θ_0+θ_1x_1+θ_2x_2+θ_3x_1^2+θ_4x_2^2)\)是[-1 0 0 1 1],则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。
我们可以用非常复杂的模型来适应非常复杂形状的判定边界。
代价函数
接下来我们要介绍如何拟合逻辑回归模型的参数\(θ\)。具体来说,我要定义用来拟合参数的优化目标或者叫代价函数,这便是监督学习问题中的逻辑回归模型的拟合问题。
对于线性回归模型,我们定义的代价函数是所有模型误差的平方和。理论上来说,我们也可以对逻辑回归模型沿用这个定义,但是问题在于:当我们将\(h_θ(x)=\frac{1}{1+e^{-θ^TX}}\)代入到这样定义了的代价函数中时,我们得到的代价函数将是一个非凸函数(no-convex function).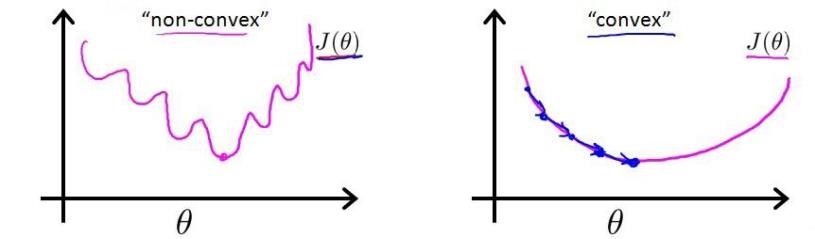
这意味着我们的代价函数有许多局部最小值,这将影响梯度下降算法寻找全局最小值。
线性回归的代价函数为:
$$J(\theta)=\frac{1}{2m}\sum_{i=1}^m\left(h_{\theta}(x^{(i)})-y^{(i)}\right)^2$$
我们重新定义逻辑回归的代价函数为:
$$J(\theta)=\frac{1}{m}\sum_{i=1}^mCost\left(h_{\theta}(x^{(i)}),y^{(i)}\right)$$
其中:
$$
\begin{eqnarray}
Cost(h_\theta(x),y)=
\begin{cases}
-log(h_\theta(x)), y=1 \cr -log(1-h_\theta(x)), y=0
\end{cases}
\end{eqnarray}
$$
\(h_θ(x)\)与\(Cost(h_θ(x),y)\)之间的关系如下图所示: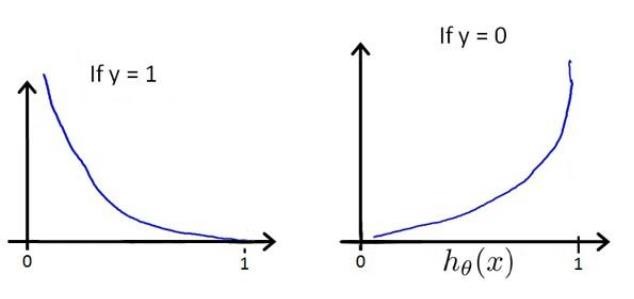
这样构建的\(Cost(h_θ(x),y)\)函数的特点是:当实际的y=1且\(h_θ\)也为1时误差为 0,当y=1但\(h_θ\)不为1时误差随着\(h_θ\)的变小而变大;当实际的y=0且\(h_θ\)也为0时,代价为0,当y=0但\(h_θ\)不为0时误差随着\(h_θ\)的变大而变大。
将构建的Cost(hθ(x),y)简化如下:
$$Cost(h_θ(x),y)=-y*log(h_θ(x))-(1-y)*log(1-h_θ(x))$$
代入代价函数得到:
$$J(θ)=-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log(h_θ(x^{(i)}))+(1-y^{(i)})log(1-h_θ(x^{(i)}))\right)$$
在得到这样一个代价函数以后,我们便可以用梯度下降算法来求得能使代价函数最小的参数了。算法为:
repeat until convergence{
$$\theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta) $$
}
求导后得到:
repeat until convergence{
$$\theta_j:=\theta_j-\alpha\sum_{i=1}^m\left((h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}\right) $$
}
推导过程
所给的代价函数:
$$J(θ)=-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log(h_θ(x^{(i)}))+(1-y^{(i)})log(1-h_θ(x^{(i)}))\right)$$
其中:
\(h_θ(x^{(i)})=\frac{1}{1+e^{-θ^TX}}\)
令\(z=θ^Tx=θ_0+θ_1x_1+θ_2x_2+…+θ_nx_n\)
则\(\frac{\partial z}{\partial(θ_j)}=x_j^{(i)}\)
\(h_θ(x^{(i)})=\frac{1}{1+e^{-z}}=\frac{e^z}{1+e^z}\)
$$J(θ)=-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log(h_θ(x^{(i)}))+(1-y^{(i)})log(1-h_θ(x^{(i)}))\right)\\\\
=-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log(h_θ(x^{(i)}))-y^{(i)}log(1-h_θ(x^{(i)}))+log(1-h_θ(x^{(i)}))\right) \\\\
= -\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log\left(\frac{h_θ(x^{(i)})}{1-h_θ(x^{(i)})}\right)+log(1-h_θ(x^{(i)}))\right) \\\\
= -\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log\left(\frac{\frac{e^{z^{(i)}}}{1+e^{z^{(i)}}}}{1-\frac{e^{z^{(i)}}}{1+e^{z^{(i)}}}}\right)+log(1-\frac{e^{z^{(i)}}}{1+e^{z^{(i)}}})\right) \\\\
= -\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}z^{(i)}-log(1+e^{z^{(i)}})\right)
$$
$$
J’(θ)= -\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}\frac{\partial z^{(i)}}{\partialθ_j}-\frac{e^{z^{(i)}}}{1+e^{z^{(i)}}}\frac{\partial z^{(i)}}{\partialθ_j}\right) \\\\
= -\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}-h_θ(x^{(i)})\right)\frac{\partial z^{(i)}}{\partialθ_j} \\\\
= \frac{1}{m}\sum_{i=1}^m\left((h_θ(x^{(i)})-y^{(i)})x_j^{(i)}\right)
$$
注:虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样,但是这里的\(h_θ(x)=g(θ^TX)\)与线性回归中不同,所以实际上是不一样的。另外,在运行梯度下降算法之T前,进行特征缩放依旧是非常必要的。
一些梯度下降算法之外的选择:除了梯度下降算法以外,还有一些常被用来令代价函数最小的算法,这些算法更加复杂和优越,而且通常不需要人工选择学习率,通常比梯度下降算法要更加快速。这些算法有:共轭梯度(Conjugate Gradient),局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS)。
多类别分类 1对多
我们将谈到如何使用逻辑回归(logistic regression)来解决多类别分类问题,具体来说,我想通过一个叫做”一对多” (one-vs-all)的分类算法。
先看这样一些例子。
- 第一个例子:假如说你现在需要一个学习算法能自动地将邮件归类到不同的文件夹里,或者说可以自动地加上标签,那么,你也许需要一些不同的文件夹,或者不同的标签来完成
这件事,来区分开来自工作的邮件、来自朋友的邮件、来自家人的邮件或者是有关兴趣爱好的邮件,那么,我们就有了这样一个分类问题:其类别有四个,分别用y=1、y=2、y=3、y=4来代表。 - 第二个例子是有关药物诊断的,如果一个病人因为鼻塞来到你的诊所,他可能并没有生病,用y=1这个类别来代表;或者患了感冒,用y=2来代表;或者得了流感用y=3来代表。
- 第三个例子:如果你正在做有关天气的机器学习分类问题,那么你可能想要区分哪些天是晴天、多云、雨天、或者下雪天,对上述所有的例子,y可以取一个很小的数值,一个相对”谨慎”的数值,比如1到3、1到4或者其它数值。
以上说的都是多类分类问题。
然而对于之前的一个二元分类问题,我们的数据看起来可能是像这样: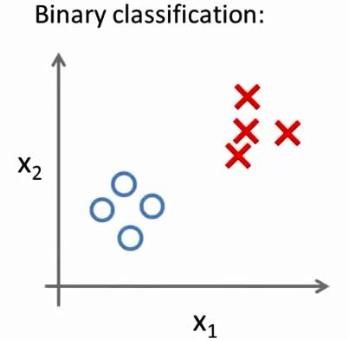
对于一个多类分类问题,我们的数据集或许看起来像这样: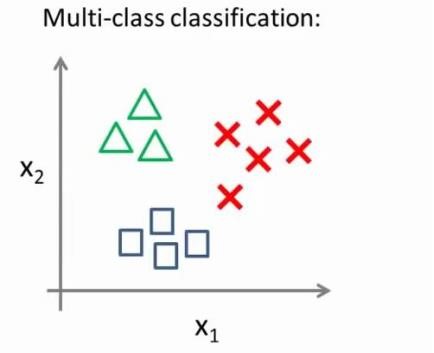
我用三种不同的符号来代表三个类别,问题就是给出三个类型的数据集,我们如何得到一个学习算法来进行分类呢?
我们现在已经知道如何进行二元分类,可以使用逻辑回归,对于直线或许你也知道,可以将数据集一分为二为正类和负类。用一对多的分类思想,我们可以将其用在多类分类问题上。
下面将介绍如何进行一对多的分类工作,有时这个方法也被称为”一对余”方法。
现在我们有一个训练集,好比上图表示的有三个类别,我们用三角形表示y=1,方框表示 y=2,叉叉表示y=3。我们下面要做的就是使用一个训练集,将其分成三个二元分类问题。我们先从用三角形代表的类别1开始,实际上我们可以创建一个,新的”伪”训练集,类型2和类型3定为负类,类型1设定为正类,我们创建一个新的训练集,如下图所示的那样,我们要拟合出一个合适的分类器。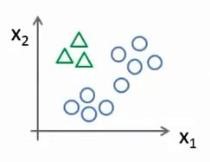
这里的三角形是正样本,而圆形代表负样本。可以这样想,设置三角形的值为1,圆形的值为0,下面我们来训练一个标准的逻辑回归分类器,这样我们就得到一个正边界。
为了能实现这样的转变,我们将多个类中的一个类标记为正向类(y=1),然后将其他所有类都标记为负向类,这个模型记作\(h_\theta^{(1)}(x)\)。
接着,类似地第我们选择另一个类标记为正向类(y=2),再将其它类都标记为负向类,将这个模型记作\(h_\theta^{(2)}(x)\),依此类推。
最后我们得到一系列的模型简记为:\(h_\theta^{(i)}(x)=p(y=i|x;\theta)\)
最后,在我们需要做预测时,我们将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量。
总之,我们已经把要做的做完了,现在要做的就是训练这个逻辑回归分类器:\(h_\theta^{(i)}(x)\)其中i对应每一个可能的y=i,最后,为了做出预测,我们给出输入一个新的x值,用这个做预测。我们要做的就是在我们三个分类器里面输入x,然后我们选择一个让\(h_\theta^{(i)}(x)\)最大的i,即\(\max_{i}h_\theta^{(i)}(x)\)
现在知道了基本的挑选分类器的方法,选择出哪一个分类器是可信度最高效果最好的,那么就可认为得到一个正确的分类,无论i值是多少,我们都有最高的概率值,我们预测y就是那个值。这就是多类别分类问题,以及一对多的方法,通过这个小方法,现在也可以将逻辑回归分类器用在多类分类的问题上。
正则化
到现在为止,我们已经学习了几种不同的学习算法,包括线性回归和逻辑回归,它们能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习应用时,会遇到过度拟合 (over-fitting)的问题,可能会导致它们效果很差。
接下来,我们将谈论一种称为正则化(regularization)的技术,它可以改善或者减少过度拟合问题。
下图是一个回归问题的例子: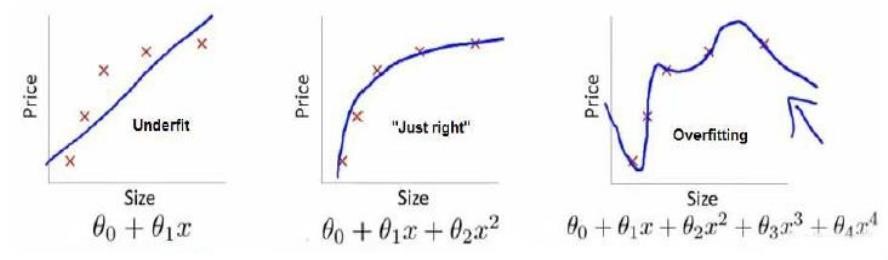
第一个模型是一个线性模型,欠拟合,不能很好地适应我们的训练集;第三个模型是一个四次方的模型,过于强调拟合原始数据,而丢失了算法的本质:预测新数据。我们可以看出,若给出一个新的值使之预测,它将表现的很差,是过拟合,虽然能非常好地适应我们的训练集但在新输入变量进行预测时可能会效果不好;而中间的模型似乎最合适。
分类问题中也存在这样的问题: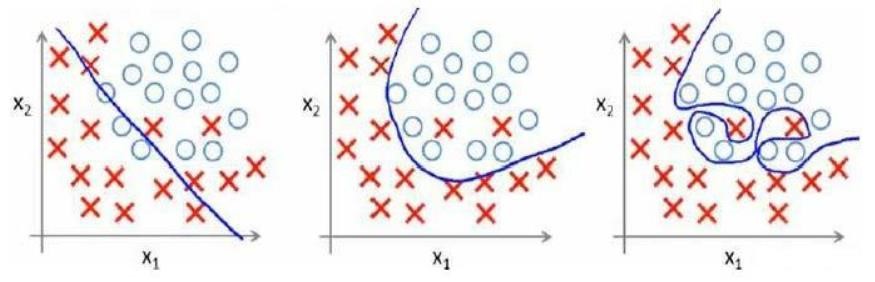
就以多项式理解,x的次数越高,拟合的越好,但相应的预测的能力就可能变差。
问题是,如果我们发现了过拟合问题,应该如何处理?
- 丢弃一些不能帮助我们正确预测的特征。可以是手工选择保留哪些特征,或者使用一些模型选择的算法来帮忙(例如PCA)
- 正则化。保留所有的特征,但是减少参数的大小(magnitude)。
代价函数
上面的回归问题中如果我们的模型是:
$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+\theta_3x_3^3+\theta_4x_4^4$$
我们可以从之前的事例中看出,正是那些高次项导致了过拟合的产生,所以如果我们能让这些高次项的系数接近于0的话,我们就能很好的拟合了。
所以我们要做的就是在一定程度上减小这些参数θ的值,这就是正则化的基本方法。我们决定要减少\(θ_3\)和\(θ_4\)的大小,我们要做的便是修改代价函数,在其中\(θ_3\)和\(θ_4\)设置一点惩罚。这样做的话,我们在尝试最小化代价时也需要将这个惩罚纳入考虑中,并最终导致选择较小一些的\(θ_3\)和\(θ_4\)。修改后的代价函数如下:
$$\min_θ\frac{1}{2m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2+1000θ_3^2+10000θ_4^2$$
通过这样的代价函数选择出的\(θ_3\)和\(θ_4\)对预测结果的影响就比之前要小许多。假如我们有非常多的特征,我们并不知道其中哪些特征我们要惩罚,我们将对所有的特征进行惩罚,并且让代价函数最优化的软件来选择这些惩罚的程度。这样的结果是得到了一个较为简单的能防止过拟合问题的假设:
$$J(θ)=\frac{1}{2m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^nθ_j^2$$
其中λ又称为正则化参数(Regularization Parameter)。注:根据惯例,我们不对\(θ_0\)进行惩罚。经过正则化处理的模型与原模型的可能对比如下图所示: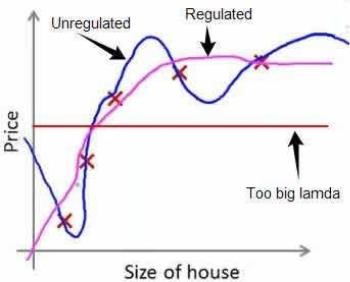
如果选择的正则化参数λ过大,则会把所有的参数都最小化了,导致模型变成\(h_θ(x)=θ_0\).也就是上图中红色直线所示的情况,造成欠拟合。
那为什么增加的一项\(\lambda\sum_{j=1}^nθ_j^2\),可以使θ的值减小呢?
因为如果我们令λ的值很大的话,为了使Cost Function尽可能的小,所有的θ的值(不包括 \(θ_0\))都会在一定程度上减小。
但若λ的值太大了,那么θ(不包括\(θ_0\))都会趋近于0,这样我们所得到的只能是一条平行于x轴的直线。
所以对于正则化,我们要取一个合理的λ的值,这样才能更好的应用正则化。
回顾一下代价函数,为了使用正则化,让我们把这些概念应用到到线性回归和逻辑回归中去,那么我们就可以让他们避免过度拟合了。正则化线性回归
对于线性回归的求解,我们之前推导了两种学习算法:一种基于梯度下降,一种基于正规方程。
正则化线性回归的代价函数为:
$$J(θ)=\frac{1}{2m}\sum_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^nθ_j^2$$
如果我们要使用梯度下降法令这个代价函数最小化,因为我们未对\(θ_0\)进行正则化,所以梯度下降算法将分两种情形:
repeat until convergence{
$$\theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m((h_{\theta}(x^{(i)})-y^{(i)}).x_0^{(i)}) \\\
\theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^m((h_{\theta}(x^{(i)})-y^{(i)})*x_j^{(i)}+\frac{\lambda}{m}\theta_j) \\\\
for j=1,2,…,n$$
}
对上面j=1,2…n时的更新式子进行调整可得:
$$\theta_j:=\theta_j(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$
可以看出,正则化线性回归的梯度下降算法的变化在于,每次都在原有算法更新规则的基础上令θ值减少了一个额外的值。
我们同样也可以利用正规方程来求解正则化线性回归模型,方法如下所示:
$$θ=\left(X^TX+\lambda I\right)^{-1}X^Ty \\\\
其中I为对角矩阵,并且第一个元素为0,其余对角元素都为1$$正则化的逻辑回归模型
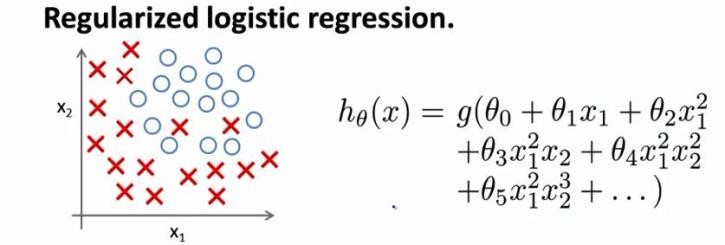
同样对于逻辑回归,我们也给代价函数增加一个正则化的表达式,得到代价函数:
$$J(θ)=-\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}log(h_θ(x^{(i)}))+(1-y^{(i)})log(1-h_θ(x^{(i)}))\right)+\frac{\lambda}{2m}\sum_{j=1}^nθ_j^2$$
要最小化该代价函数,通过求导,得出梯度下降算法为:
repeat until convergence{
$$\theta_0:=\theta_0-\alpha\frac{1}{m}\sum_{i=1}^m((h_{\theta}(x^{(i)})-y^{(i)}).x_0^{(i)}) \\\
\theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^m((h_{\theta}(x^{(i)})-y^{(i)})*x_j^{(i)}+\frac{\lambda}{m}\theta_j) \\\\
for j=1,2,…,n$$
}
注:看上去同线性回归一样,但是逻辑回归\(h_θ(x)=g(θ^TX)\),而线性回归\(h_θ(x)=θ^TX\),所以二者不同。
广义线性模型与逻辑回归
广义线性模型的介绍见:线性回归-拓展 广义线性模型与线性回归
实际上,逻辑回归中:我们有如下假设:
$$y|x;θ \sim Bernoulli(\phi)$$
即,假设y的条件概率服从伯努利分布,伯努利分布也是广义线性模型的一种特例。
Bernoulli分布的指数分布簇形式
广义线性模型的指数分布簇形式:
$$p(y;\eta)=b(y)exp(\eta^{T}T(y)-a(\eta))$$
伯努利分布:
$$p(y=1;\phi)=\phi; \ p(y=0;\phi)=1-\phi$$
=>
$$p(y;\phi)=\phi^y(1-\phi)^{1-y} \\\\
=exp(ylog\phi+(1-y)log(1-\phi)) \\\\
=exp\left( \left(log\left(\frac{\phi}{1-\phi}\right)\right)y+log(1-\phi)\right)
$$
即:在如下参数下,广义线性模型是伯努利分布
$$\eta=log(\frac{\phi}{1-\phi}) => \phi = \frac{1}{1+e^{-\eta}} \\\\
T(y)=y \\\\
a(\eta)=-log(1-\eta)=log(1+e^\eta) \\\\
b(y)=1
$$
广义线性模型推导逻辑回归
让我们重新审视一下逻辑回归,我们定义:
$$h_\theta(x)=P(y=1|x;\theta)$$
即,模型的输出就是y=1的概率,后面我们会发现\(P(y=1|x;\theta)\)实际上就是伯努利分布的参数\(\phi\)。由上式有:
$$P(y=0|x;\theta)=1-h_\theta(x)$$
我们将两个式子合并成一个式子:有:
$$P(y|x;\theta)=h_\theta(x)^y+(1-h_\theta(x))^{1-y}$$
显然,y=1时,上式变为\(P(y=1|x;\theta)=h_\theta(x)\); y=0时,上式变为\(P(y=0|x;\theta)=1-h_\theta(x)\)
使用极大似然估计,得到:
$$L(\theta)=P(y|X;\theta)=\prod_{i=1}^mP(y^{(i)}|x^{(i)};\theta) \\\\=\prod_{i=1}^m\left(h_\theta(x^{(i)})^{y^{(i)}}+(1-h_\theta(x^{(i)}))^{1-y^{(i)}}\right)$$
两边取对数得到:
$$\ell(\theta)=log(L(\theta))=\sum_{i=1}^m\left(y^{(i)}log(h_θ(x^{(i)}))+(1-y^{(i)})log(1-h_θ(x^{(i)}))\right)$$
这就是上文的代价函数。
下面是推导:
- step1: \(y|x;\theta \sim Bernoulli(\phi)\)
- step2: 由假设2: \(h(x)=E[y|x]\) 得到:
$$h_\theta(x)=E[y|x;\Theta]=p(y=1|x;\theta)\\\\
=\phi \\\\
=\frac{1}{1+e^{-\eta}} \\\\
=\frac{1}{1+e^{-\Theta^Tx}} \\\\
其中, E[y|x;\Theta]=\phi由假设1得到;\\\\
\phi=\frac{1}{1+e^{-\eta}}由伯努利分布对应的广义线性模型参数得到;\\\\
\eta = \Theta^Tx由假设3得到。
$$
注:可以看出Sigmoid function得到的实际上就是\(\phi\)的值,也就是预测y=1的概率。
拓展——softmax回归
多项式分布
首先,y的取值有多个,\(y \in {1,2…,k}\),参数也相应的有k个,即\({\phi_1,\phi_2,…,\phi_k}\),则:
$$P(y=i)=\phi_i$$
我们将\(\phi_k\)改写成:
$$\phi_k=1-(\phi_1+\phi_2+…+\phi_{k-1})$$
因此可以视作只有k-1个参数,\(\phi_1,\phi_2,…,\phi_{k-1}\)
指数分布簇形式推导
首先定义T(y):
$$T(1)=[1 \ 0 \ … \ 0]^T$$
$$T(2)=[0 \ 1 \ … \ 0]^T$$
$$T(k-1)=[0 \ 0 \ … \ 1]^T$$
$$T(k)=[0 \ 0 \ … \ 0]^T$$
定义指示函数:
\(I\{True\}=1, I\{False\}=0\)
我们使用标志:
\(T(y)_i\)表示向量\(T(y)\)的第\(i\)个元素,则:
$$T(y)_i=I\{y=i\}$$
根据多项式分布:
$$P(y)=\phi_1^{I\{y=1\}}\phi_2^{I\{y=2\}}…\phi_k^{I\{y=k\}} \\\\
=\phi_1^{(T(y))_1}\phi_2^{(T(y))_2}…\phi_{k=1}^{(T(y))_{k-1}}\phi_k^{1-\sum_{j=1}^{k-1}(T(y))_j} \\\\
=exp\left((T(y))_1 log(\phi_1) + (T(y))_2 log(\phi_2))+…+\left(1-\sum_{j=1}^{k-1}(T(y))_j\right)log(\phi_k)\right) \\\\
=exp\left((T(y))_1 log(\frac{\phi_1}{\phi_k}) + (T(y))_2 log(\frac{\phi_2}{\phi_k}) + … + (T(y))_{k-1} log(\frac{\phi_{k-1}}{\phi_k})+log(\phi_k) \right)
=b(y)exp(\eta^T T(y)-a(\eta)) \\\\
$$
其中,
$$
\eta=\begin{bmatrix} log(\frac{\phi_i}{\phi_k}) \\\ … \\\ log(\frac{\phi_{k-1}}{\phi_k}) \end{bmatrix} \\\\
a(\eta)=-log(\phi_k) \\\\
b(y)=1
$$
根据上面这些式子,可以将多项式分布转化成指数分布簇形式。
我们有:for(i=1,…,k):
$$\eta_i=log\frac{\phi_i}{\phi_k}$$
为了方便,我们定义\(\eta_k=log\frac{\phi_k}{\phi_k}=0\)
我们有:
$$e^{\eta_i}=\frac{\phi_i}{\phi_k}$$
则:
$$\phi_ke^{\eta_i}=\phi_i \ \ \ \ \ \ \ \ (1)$$
$$\phi_k\sum_{i=1}^ke^{\eta_i}=\sum_{i=1}^k \phi_i=1$$
$$\phi_k=\frac{1}{\sum_{i=1}^k e^{\eta_i}}$$
代回到(1)式,得到:
$$\phi_i=\frac{e^{\eta_i}}{\sum_{j=1}^k e^{\eta_j}}$$
我们将\(\phi\)和\(\eta\)关系倒过来,可以得到:
$$p(y=i|x;\theta)=\phi_i=\frac{e^{\eta_i}}{\sum_{j=1}^{k}e^{\eta_j}} \\\\
=\frac{e^{\theta_i^T X}}{\sum_{j=1}^{k}e^{\theta_j^T X}}
$$
前面提到,\(\eta_k=0\),故上式也可以写作:
$$p(y=i|x;\theta)=\phi_i=\frac{e^{\eta_i}}{1+\sum_{j=1}^{k-1}e^{\eta_j}} \\\ =\frac{e^{\theta_i^T X}}{1+\sum_{j=1}^{k-1}e^{\theta_j^T X}}
$$
这和逻辑回归的样子非常像:
$$\phi_1=\frac{1}{1+e^{-\theta^T X}}=\frac{e^{\theta^T X}}{1+e^{\theta^T X}}$$
注意,softmax回归中的\(\theta_i,…,\theta_{k-1} \in \mathbb{R^{n+1}}\),即n+1维向量。
所以我们的学习算法:
$$h_\theta(x)=E[T(y)|x;\theta] \\\\
=E\left[\begin{bmatrix} I\{y=1\} \\\ … \\\ I\{y=k-1\} \end{bmatrix} | x;\theta\right] = \begin{bmatrix} \phi_1 \\\ … \\\ \phi_{k-1} \end{bmatrix} \\\\
= \begin{bmatrix} \frac{e^{\theta_i^T X}}{\sum_{j=1}^{k}e^{\theta_j^T X}} \\\ … \\\ \frac{e^{\theta_{k-1}^T X}}{\sum_{j=1}^{k}e^{\theta_j^T X}} \end{bmatrix}
$$
最后只需要使用极大似然法拟合参数即可:
$$\ell(\theta)=\sum_{i=1}^m log \ p(y^{(i)}|x^{(i)};\theta) \\\\
=\sum_{i=1}^m log \prod_{l=1}^k \left(\frac{e^{\theta_{l}^T X}}{\sum_{j=1}^{k}e^{\theta_j^T X}}\right)^{I\{y_i=l\}}$$

