前面我们介绍了时间序列模型的概念、数学基础等。本文将接着介绍时间序列模型的更多理论性质,包括一般线性过程(general linear process),自回归模型AR(the autoregressive model),移动平均模型MA(the moving average)以及ARMA模型。
一般线性过程
定义:
- 时间序列\({Z_t}\)是线性(linear)的,当且仅当\(Z_t\)的值是白噪声系列的线性函数。
- 时间序列\({Z_t}\)是有因果的(causal),当且仅当\(Z_t\)的值只受到目前为止的信息影响,换句话说\(Z_t\)是独立于未来信息\(a_s\)的,s>t
- 时间序列模型通常是由白噪声驱动的,即\({a_t}\), 时间序列是\({a_t}\)的函数。随机变量\(a_t\)可以被时刻t的信息所解释。白噪声通常叫做新息序列(innovation sequence)或信息序列(information sequence).
因此,一个线性的、有因果的、平稳的时间序列也被称作一般线性过程(a general linear process)。
一般线性过程具有如下形式:
$$Z_t=\mu+\sum_{j=0}^{\infty}\psi_j a_{t-j}=\mu+\psi_0a_t+\psi_1a_{t-1}+\psi_2a_{t-2} \\\\
其中,{a_t} \sim WN(0,\sigma_a^2) \ and \ \sigma_a^2\sum_{j=0}^{\infty}\psi_j^2<\infty$$
不失一般性,我们可以设\(\psi_0=1\)
均值,自协方差,自相关系数
一般线性过程:
$$E(Z_t)=\mu$$
$$\gamma_0=var(Z_t)=\sigma_a^2\sum_{j=0}^{\infty}\psi_j^2<\infty$$
$$\gamma_k=cov(Z_t,Z_{t-k})=\sigma_a^2\sum_{j=0}^{\infty}\psi_j\psi_{j+k},k \geq 0$$
$$\rho_k=\frac{cov(Z_t,Z_{t-k})}{var(Z_t)}=\frac{\sum_{j=0}^{\infty}\psi_j\psi_{j+k}}{\sum_{j=0}^{\infty}\psi_j^2},k > 0$$
移动平均MA过程
定义:q阶移动平均过程,简记为:
$$Z_t=\theta_0+a_t-\theta_1a_{t-1}-\theta_2a_{t-2}-…-\theta_qa_{t-q} \\\\
其中,q \in \mathbb{N}, 并且 {a_t} \sim WN(0,\sigma_a^2)$$
- 如果\(\theta_0=0\),则0阶移动平均过程实际上就是白噪声序列,此时\(Z_t=a_t\)
- 移动平均过程是一种特殊的一般线性过程。因为它是线性,因果和平稳的
一阶移动平均过程MA(1)
$$Z_t=\theta_0+a_t-\theta a_{t-1}$$
- 显然,\(E(Z_t)=\theta_0\)
- \(\gamma_0=var(Z_t)=\sigma_a^2(1+\theta^2)\)
- \(\gamma_1=cov(Z_t,Z_{t-1})=cov(a_t-\theta a_{t-1},a_{t-1}-\theta a_{t-2}) = cov(-\theta a_{t-1},-\theta a_{t-2})=-\theta \sigma_a^2\)
- \(\rho_1 = \frac{-\theta}{1+\theta^2}\)
- \(\rho_2=cov(Z_t,Z_{t-2})=cov(a_t-\theta a_{t-1},a_{t-2}-\theta a_{t-3})=0\)
- 同理,因为\(Z_t和Z_{t-2}\)之间不存在共同的下标,故\(\rho_2=0\)
- 故当\(k \geq 2\)时,\(\gamma_k=cov(Z_t,Z_{t-k})=0, 并且 \rho_k=0\),即这一过程在超过滞后1,就不存在相关性。这一事实在我们后续为实际数据选择合适的模型时会起到很重要作用。
二阶移动平均过程MA(2)
$$Z_t=\theta_0+a_t-\theta_1 a_{t-1}-\theta_2 a_{t-2}$$
- 显然,\(E(Z_t)=\theta_0\)
- 方差\(\gamma_0=var(Z_t)=(1+\theta_1^2+\theta_2^2)\sigma_a^2\)
- 滞后k=1的自协方差:
$$\gamma_1=cov(Z_t,Z_{t-1})=cov(a_t-\theta_1 a_{t-1}-\theta_2 a_{t-2},a_{t-1}-\theta_1 a_{t-2}-\theta_2 a_{t-3})=cov(-\theta_1 a_{t-1},a_{t-1}) + cov(-\theta_2 a_{t-2},-\theta_1 a_{t-2})=[-\theta_1+(-\theta_1)(-\theta_2)]\sigma_a^2=(-\theta_1+\theta_1 \theta_2)\sigma_a^2$$ - 滞后k=2的自协方差为:
$$\gamma_2=cov(Z_t,Z_{t-2})=cov(a_t-\theta_1 a_{t-1}-\theta_2 a_{t-2},a_{t-2}-\theta_1 a_{t-3}-\theta_2 a_{t-4})=cov(-\theta_2 a_{t-2}, a_{t-2})=-\theta_2 \sigma_a^2$$ - 同理相关系数,\(\rho_k=0, \forall k \geq 3\)
$$ \begin{eqnarray} \rho=\begin{cases} \rho_1=\frac{-\theta_1+\theta_1 \theta_2}{1+\theta_1^2+\theta_2^2} \cr \rho_2=\frac{-\theta_2}{1+\theta_1^2+\theta_2^2} \cr \rho_k=0, \forall k \geq 3 \end{cases} \end{eqnarray}$$
q阶移动平均过程MA(q)
$$Z_t=\theta_0+a_t-\theta_1a_{t-1}-\theta_2a_{t-2}-…-\theta_qa_{t-q}$$
- 均值\(\mu=\theta_0\)
- 方差\(\gamma_0=(1+\theta_1^2+\theta_2^2+…+\theta_q^2)\sigma_a^2\)
- 自协方差:
$$ \begin{eqnarray} \rho_k=\begin{cases} \frac{-\theta_k+\theta_1 \theta_{k+1}+\theta_2 \theta_{k+2}+…+\theta_{q-k} \theta_{q}}{1+\theta_1^2+\theta_2^2+…+\theta_q^2},k=1,2,…,q \cr 0, \forall k \geq q+1 \end{cases} \end{eqnarray}$$ - 自相关:
当k=q时,\(\rho_k \neq 0\); 当k>q时,\(\rho_k=0\)
我们通常说,q阶移动平均过程的自相关函数在q滞后截尾,即ACF会在lag=q时截尾(cuts off).
后向移位算子
任意时间序列上的后向移位算子B定义为:
\(BZ_t=Z_{t-1}\), \(B^kZ_t=B^{k-1}(BZ_t)=…=Z_{t-k}, \forall k \in \mathbb{Z}\)
因此,B(Z)是原始序列Z的滞后为1的序列。\(B^k(Z)是原始序列滞后为k的序列\)
特别的,\(B^0是单位算子,B^0Z=Z\)
因此:
移动平均过程:
$$Z_t=\theta_0+a_t-\theta_1a_{t-1}-\theta_2a_{t-2}-…-\theta_qa_{t-q}$$
可以被重写为:
$$Z_t=(1-\theta_1B-\theta_2B^2-…-\theta_qB^q)a_t=\theta(B)a_t$$
其中,\(\theta(x)=1-\theta_1x-…-\theta_qx^q\)是MA移动平均的特征多项式
自回归过程AR
p阶自回归模型AR(p)定义为:
$$Z_t=\theta_0+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+…+\phi_p Z_{t-p} + a_t \\\\
其中,p \geq 0,且p为整数。 \phi是参数。{a_t} \sim WN(0,\sigma_a^2)
$$
模型可以被重写为:
$$\phi(B)Z_t=\theta_0+a_t \\\\
其中,\phi(x)=1-\phi_1x-\phi_2x^2-…-\phi_px^p是AR的特征多项式$$
理论
AR(p)模型有一个唯一的平稳性解,只有当下面AR特征方程的所有根都在单位圆外时。
$$\phi(x)=1-\phi_1x-\phi_2x^2-…-\phi_px^p=0$$
- 求解唯一平稳性解叫做AR(p)自回归过程
- 上述条件称作平稳性条件
- 对于一个复杂的z值,如果\(\vert z \vert > 1\),我们称它是在单位圆外。
- 例子:找出AR(1)模型的平稳性条件:
\(Z_t=\phi Z_{t-1}+a_t\)
由上可得,\(1-\phi x=0\),则\(x=1/\phi\),因为需要满足|x|>1,则我们有\(|\phi| < 1\) - 例子,找出AR(1),\(Z_t=0.5Z_{t-1}+a_t\)的一般线性过程形式:
由前面AR的特征多项式可得,
$$(1-0.5B)Z_t=a_t$$
因此可以根据等比数列求和性质得到如下式子
$$Z_t=\frac{1}{1-0.5B}a_t=(1+0.5B+0.5^2B^2+…)a_t$$
进一步得到,即一般线性过程形式:
$$Z_t=a_t+0.5a_{t-1}+0.5^2a_{t-2}+…$$一般平稳性条件
$$Z_t=\theta_0+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+…+\phi_p Z_{t-p} + a_t \ (1)$$
必须满足如下条件:
$$ \begin{eqnarray} \begin{cases} \mu=\frac{1}{1-\phi_1-…-\phi_p} \cr \psi_1=\phi_1, \cr \psi_2=\phi_1\psi_1+\phi_2, \cr … \cr \psi_k=\phi_1\psi_{k-1}+\phi_2\psi_{k-2}+…+\phi_p\psi_{k-p} \end{cases} \end{eqnarray}$$
其中,\(\psi是一般线性过程的参数\)
一般线性过程是:
$$Z_t=\mu+\sum_{j=0}^{\infty}\psi_j a_{t-j}=\mu+\psi_0a_t+\psi_1a_{t-1}+\psi_2a_{t-2} \ (2)$$
要想满足平稳性,要求AR模型能够转换成一般线性过程的形式,因此通过比较(1),(2)式子,展开运算,可以得到上述一般平稳性条件
均值,自协方差,方差,自相关
$$Z_t=\theta_0+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+…+\phi_p Z_{t-p} + a_t $$
- 均值
我们对等式两边同时求均值:
$$\mu=\theta_0+\phi_1 \mu+\phi_2 \mu + …+ \phi_p \mu + 0$$
得到:
$$\mu = \frac{\theta_0}{1-\phi_1-\phi_2-…-\phi_p}$$
可以证明分母不为0. - 自相关

将两个式子等式两边对应相乘,然后再等式两边同时求自相关,根据定义,可以得到上述3.3的式子。
- 方差
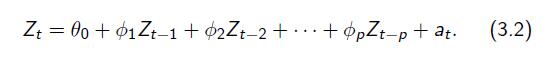

上述3.2式子和\(Z_t\)相乘后,再等式两边同时取方差,根据定义以及\(E(a_tZ_t)\)的推导,可以得到上述式子。
ARMA模型
英文全称为,the mixed autoregressive-moving average model
$$Z_t=\theta_0+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+…+\phi_p Z_{t-p} \\\\
+a_t-\theta_1a_{t-1}-\theta_2a_{t-2}-…-\theta_qa_{t-q}$$
我们称\({Z_t}\)是(p,q)阶混合自回归移动平均模型,简记为ARMA(p,q)
如果q=0,则模型退化为AR模型;如果p=0,则模型退化为MA模型。二者都是ARMA模型的特例。
为了方便,我们重写以上等式为:
$$\phi(B)Z_t=\theta_0+\theta(B)a_t \\\\
其中,\phi(x)和\theta(x)分别是AR模型和MA模型的的特征多项式$$
$$\phi(x)=1-\phi_1x-\phi_2x^2-…-\phi_px^p$$
$$\theta(x)=1-\theta_1x-\theta_2x^2-…-\theta_px^q$$
定理:如果AR多项式等式\(\phi(x)=0\)所有根都在单位圆之外,那么ARMA(p,q)模型存在唯一的平稳性解。
当存在平稳性解时,ARMA模型具备如下形式:
$$Z_t=\mu+\sum_{j=0}^\infty \psi_j a_{t-j}$$
如何求解ARMA模型平稳性条件?
考虑ARMA(1,1),则:
$$Z_t=\phi Z_{t-1}+a_t-\theta a_{t-1}$$
比较上述式子的系数可以得到:
$$\psi_0 a_t+\psi_1 a_{t-1}+ \psi_2 a_{t-2}+ … \\\\
= \phi \psi_0 a_{t-1} + \phi \psi_1 a_{t-2} + \phi \psi_2 a_{t-3} +…+a_t-\theta a_{t-1}$$
可以得出:
$$\psi_0=1$$
$$\psi_1=\phi \psi_0 - \theta = \phi - \theta$$
$$\psi_0=\phi \psi_1 = \phi^2-\phi \theta$$
$$…$$
$$\psi_k=\phi \psi_k = \phi^k - \phi^{k-1} \theta$$
一般的,对于ARMA(p,q),我们可以得到:
$$ \begin{eqnarray} \begin{cases} \psi_0=1 \cr \psi_1=-\theta_1+\phi_1, \cr \psi_2=-\theta_2+\phi_2+\phi_1 \psi_1, \cr … \cr \psi_j=\theta_j+ \phi_p \psi_{j-p}+ … + \phi_1 \psi_{j-1} \end{cases} \end{eqnarray}$$
而,
$$\mu=\frac{\theta_0}{1-\phi_1-\phi_2-…-\phi_p}$$
所以有:
$$Z_t=\mu+\sum_{j=0}^\infty \psi_j a_{t-j}$$
可逆性
为什么需要可逆性?
假设我们获取了100个观察值:
$$z_1,z_2,…,z_{100}$$
经过复杂的过程,我们得到了一个AR(1)模型:
$$Z_t=0.6Z_{t-1}+a_t$$
那么该如何解释结果呢?
如果模型变成:
$$Z_t=a_t-0.5a_{t-1}或者Z_t=0.3Z_{t-1}+a_t+0.2a_{t-1}$$
又该如何解释呢?- 定义:如果时间序列\({Z_t}\)是可逆的,则:
$$a_t=\pi_0 Z_t+\pi_1 Z_{t-1}+\pi_2 Z_{t-2}+…$$
这个性质使得我们能够基于过去观察序列获取信息序列
不失一般性,我们令\(\pi_0=1\)
AR过程总是可逆的。 - 定理:ARMA或MA模型是可逆的,当且仅当MA特征方程的根都在单位圆外。
$$\theta(x)=1-\theta_1x-\theta_2x^2-…-\theta_qx^q=0$$ - 定义:如果时间序列\({Z_t}\)是可逆的,则定义:
$$Z_t=a_t-\pi_1Z_{t-1}-\pi_2Z_{t-2}-…$$
为该时间序列的AR表示(autoregressive representation)。
- 定义:如果时间序列\({Z_t}\)是可逆的,则:
注意:可以发现求解AR表示和求解AR或ARMA模型的唯一平稳性解方法是一样的,同样是需要比较方程两边的系数。
相反,求解AR或ARMA模型的唯一平稳性解也叫做AR或ARMA模型的MA表示。

