前面花了两章篇幅介绍了时间序列模型的数学基础。 ARIMA时间序列模型(一)和ARIMA时间序列模型(二) 。本文重点介绍使用python开源库进行时间序列模型实践。
基本概念
回顾一下自回归移动平均模型ARMA,它主要由两部分组成:AR代表p阶自回归过程,MA代表q阶移动平均过程,形式如下:
$$Z_t=\theta_0+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+…+\phi_p Z_{t-p} \\\\
+a_t-\theta_1a_{t-1}-\theta_2a_{t-2}-…-\theta_qa_{t-q}$$
为了方便,我们重写以上等式为:
$$\phi(B)Z_t=\theta_0+\theta(B)a_t \\\\
其中,\phi(x)和\theta(x)分别是AR模型和MA模型的的特征多项式$$
$$\phi(x)=1-\phi_1x-\phi_2x^2-…-\phi_px^p$$
$$\theta(x)=1-\theta_1x-\theta_2x^2-…-\theta_px^q$$
根据前两篇的分析,我们总结ARMA模型的性质如下: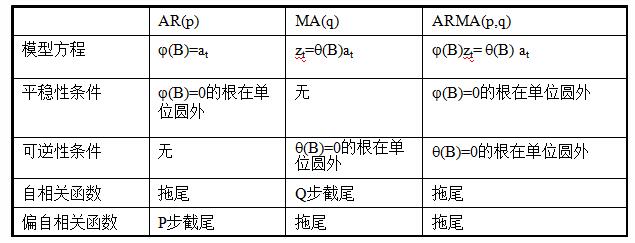
p值检验
在开始之前,我们首先回顾一下p值检验。
一般地,用X表示检验的统计量,当H0为真时,可由样本数据计算出该统计量的值C,根据检验统计量X的具体分布,可求出P值。具体地说:
- 左侧检验的P值为检验统计量X小于样本统计值C的概率,即:P = P{ X < C}
- 右侧检验的P值为检验统计量X大于样本统计值C的概率:P = P{ X > C}
- 双侧检验的P值为检验统计量X落在样本统计值C为端点的尾部区域内的概率的2倍:P = 2P{ X > C} (当C位于分布曲线的右端时) 或P = 2P{ X< C}(当C位于分布曲线的左端时) 。若X服从正态分布和t分布,其分布曲线是关于纵轴对称的,故其P值可表示为P=P{|X|>C}。
计算出P值后,将给定的显著性水平α与P值比较,就可作出检验的结论:
如果\(p < α\)值,则在显著性水平α下拒绝原假设。
如果\(P \geq α\)值,则在显著性水平α下接受原假设。
pandas数据操作
使用pandas来加载数据,并对数据索引进行转换,使用日期作为索引。
1 | dateparse = lambda dates:pd.datetime.strptime(dates,'%Y-%m') |
接着绘制数据:
1 | ts = data['#Passengers'] |
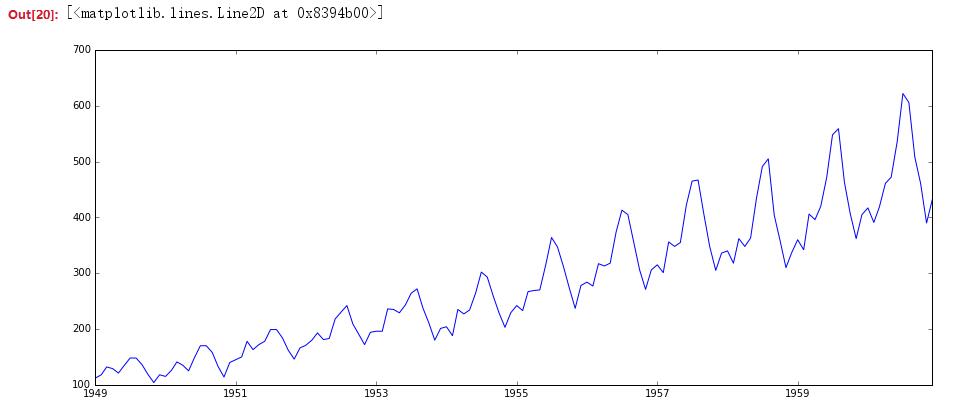
非常清晰的看到,随着季节性的变动,飞机乘客的数量总体上是在不断增长的。但是,不是经常都可以获得这样清晰的视觉体验。我们可以通过下面的方法测试稳定性。
稳定性检测
- 绘制滚动统计:我们可以绘制移动平均数和移动方差,观察它是否随着时间变化。
- ADF检验:这是一种检查数据稳定性的统计测试。无效假设:时间序列是不稳定的。测试结果由测试统计量和一些置信区间的临界值组成。如果“测试统计量”少于“临界值”,我们可以拒绝无效假设,并认为序列是稳定的。或者根据前面提高的p值检验,如果p值小于显著性水平,我们可以拒绝无效假设,认为序列稳定。
滚动统计
1 | def rolling_statistics(timeseries): |
pd.rolling_mean有两个参数,第一个是输入数据,第二个是窗口大小。假设有个序列是,1 2 3 3 5 8 6 9,如果窗口大小为3,那么移动平均数计算过程如下: 第一步: (1+2+3)/3 =2; 第二步:往右移动一个数据,(2+3+3)/3=2.667; 第三步, (3+3+5)/3=3.667; 第四步:(3+5+8)/3=5.333; 第四步: (5+8+6)/3=6.333; 第五步;(8+6+9)/3=7.667; 因此移动平均数序列为: NA NA 2 2.667 3.667 5.3333 6.333 7.667. 共用n-windows+1个数。
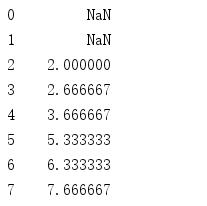
移动标准差类似,只不过把求平均变成了求标准差。
绘图如下:可以看出移动平均数仍然是上升趋势,而移动标准差相对比较平稳。
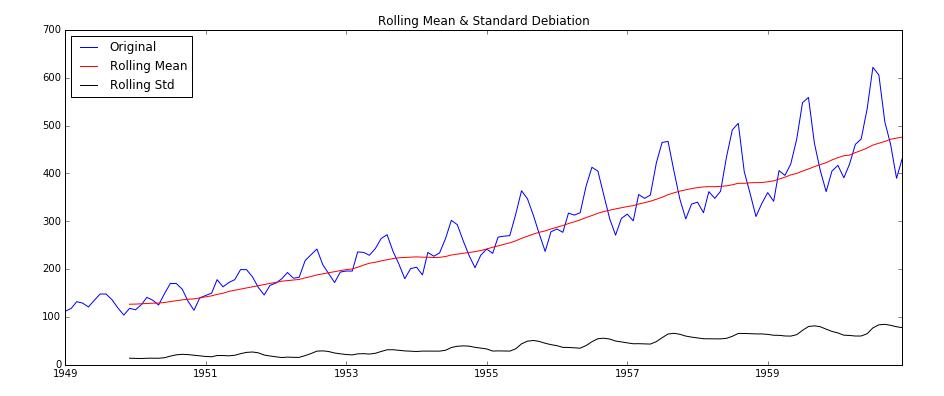
ADF检验
1 | from statsmodels.tsa.stattools import adfuller |
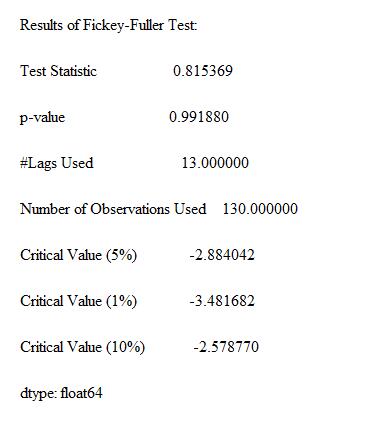
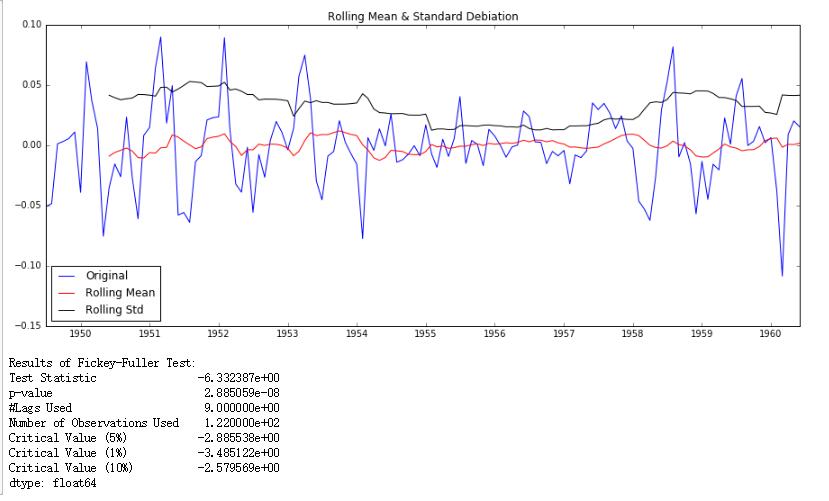
上述输出如何解读?
- Test statistic:代表检验统计量
- p-value:代表p值检验的概率
- Lags used:使用的滞后k,autolag=AIC时会自动选择滞后
- Number of Observations Used:样本数量
- Critical Value(5%) : 显著性水平为5%的临界值。
ADF检验
- 假设是存在单位根,即不平稳;
- 显著性水平,1%:严格拒绝原假设;5%:拒绝原假设,10%类推。
- 看P值和显著性水平a的大小,p值越小,小于显著性水平的话,就拒绝原假设,认为序列是平稳的;大于的话,不能拒绝,认为是不平稳的
- 看检验统计量和临界值,检验统计量小于临界值的话,就拒绝原假设,认为序列是平稳的;大于的话,不能拒绝,认为是不平稳的
根据上文提到的p值检验以及上面的结果,我们可以发现p=0.99>10%>5%>1%, 并且检验统计量0.815>>-2.58>-2.88>-3.48,因此可以认定原序列不平稳。
先让我们弄明白是什么导致时间序列不稳定。两个主要原因。
- 趋势-随着时间产生不同的平均值。举例:在飞机乘客这个案例中,我们看到总体上,飞机乘客的数量是在不断增长的。
- 季节性-特定时间框架内的变化。举例:在特定的月份购买汽车的人数会有增加的趋势,因为车价上涨或者节假日到来。
我们的基本原理是,通过建模并估计趋势和季节性这些因素,并从时间序列中移除,来获得一个稳定的时间序列,然后再使用统计预测技术来处理时间序列,最后将预测得到的数据,通过加入趋势和季节性等约束,来回退到原始时间序列数据。
平稳性处理
消除趋势的第一个方法是转换。例如,在本例中,我们可以清楚地看到该时间序列有显著趋势。所以我们可以通过变换,惩罚较高值而不是较小值。这可以采用对数, 平方根,立方跟等等。
对数变换
1 | ts_log = np.log(ts) |
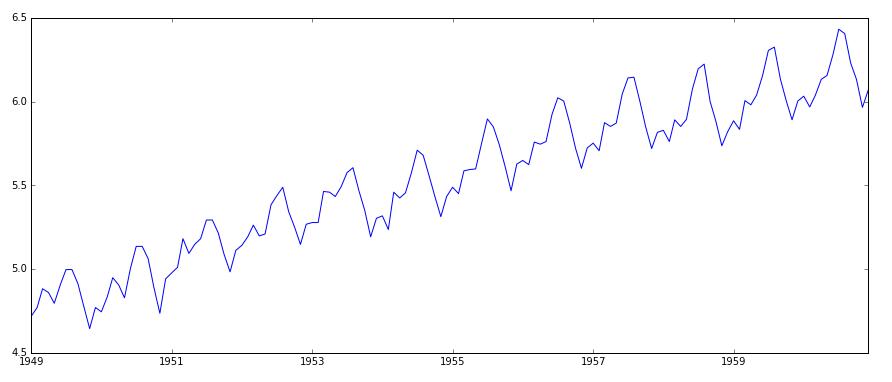
在这个例子中,很容易看到一个向前的趋势。但是它表现的不是很直观。我们可以使用一些技术来对这个趋势建模, 然后将它从序列中删除。最常用的方法有:
- 平滑-取滚动平均数
- 差分
- 分解
移动平均数
1 | moving_avg = pd.rolling_mean(ts_log,12) |
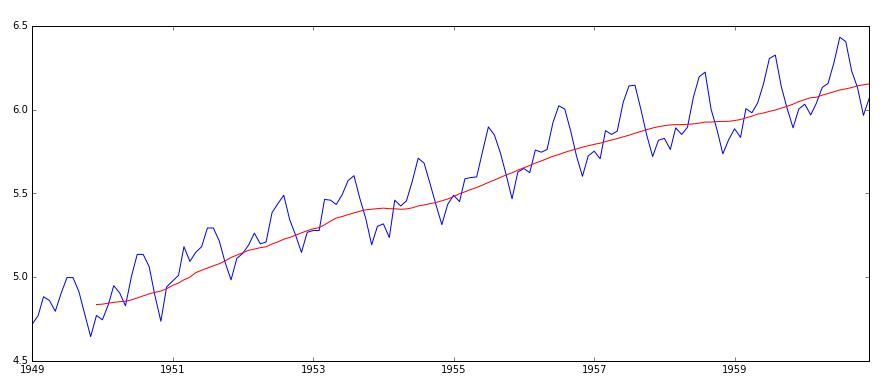
1 | #做差 |
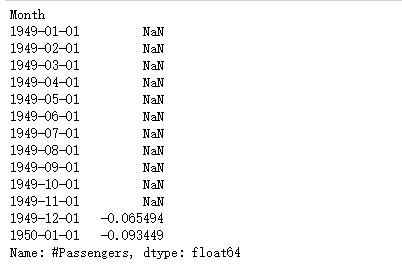
前11个数是NA
1 | adf_test(ts_log_moving_avg_diff) |
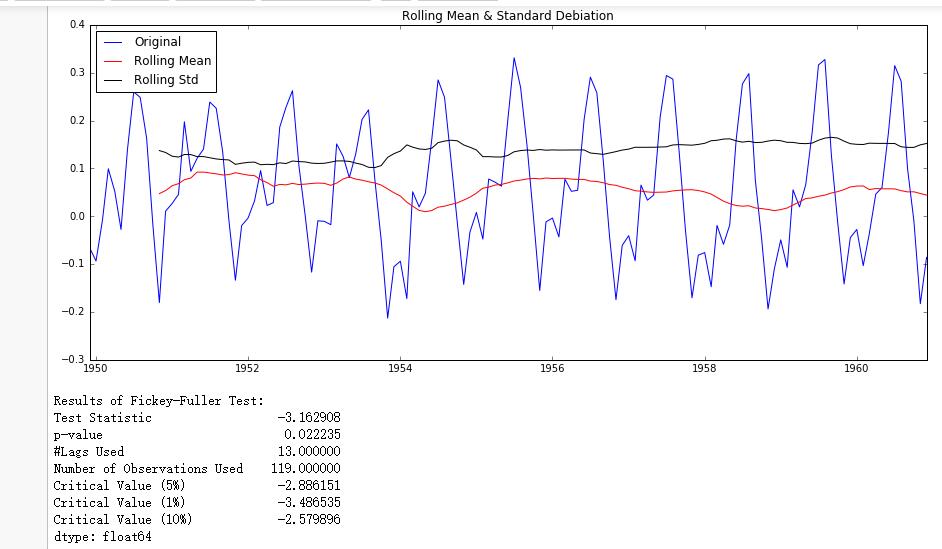
可以发现通过了5%和10%的显著性检验,即在该水平下,拒绝原假设,认为序列是平稳的,但是没有通过1%的检验。
指数加权移动平均
1 | expwighted_avg=pd.ewma(ts_log,halflife=12) |
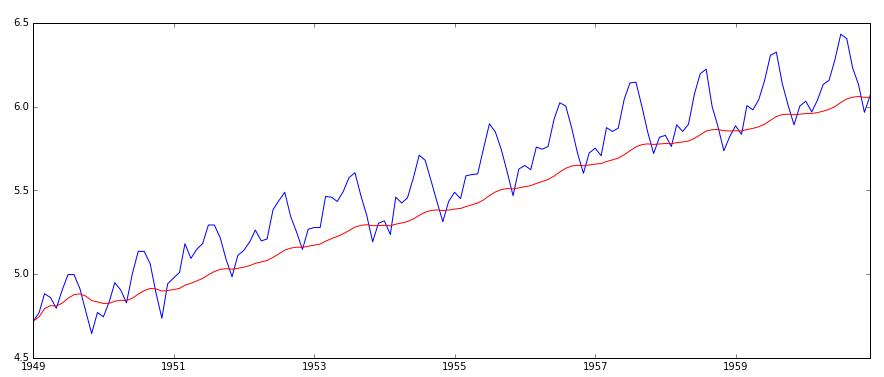
前面移动平均数需要指定window,并且对所有的数一视同仁;这里采用指数加权移动平均方法,会对当前的数据加大权重,对过去的数据减小权重。halflife半衰期,用来定义衰减量。其他参数,如跨度span和质心com也可以用来定义衰减。
1 | #做差 |
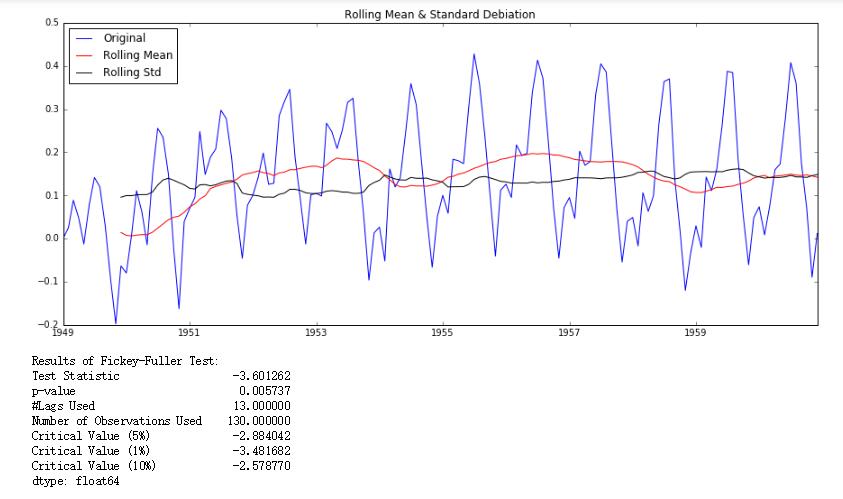
可以发现,经过指数移动平均后,再做差的结果,已经能够通过1%显著性水平检验了。
差分
1 | #步长为1的一阶差分 |
我们首先使用步长为1的一阶差分,得到如下图:
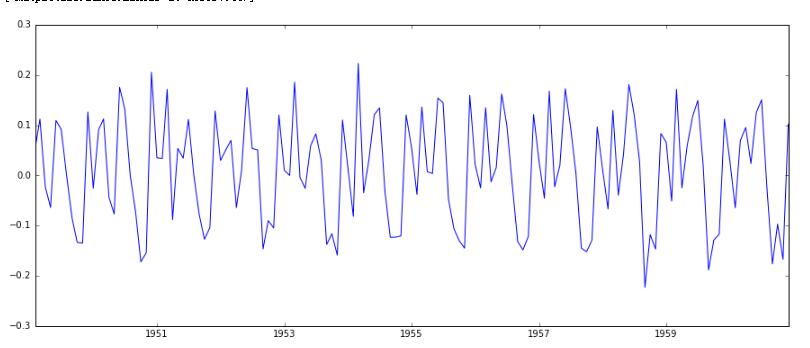
接着进行adf检验,
1 | #只通过了10%的检验 |
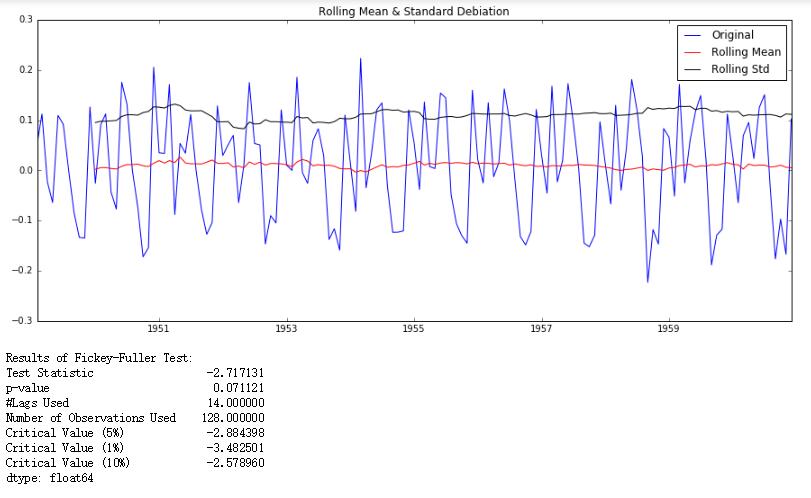
可以发现只通过了10%的显著性水平检验。
二阶差分
我们继续进行二阶差分
1 | #一阶差分:Y(k)=X(k+1)-X(k) |
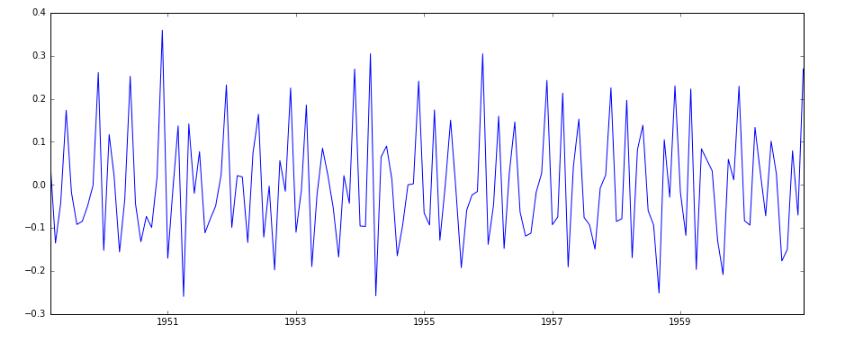
1 | #二阶差分检验 |
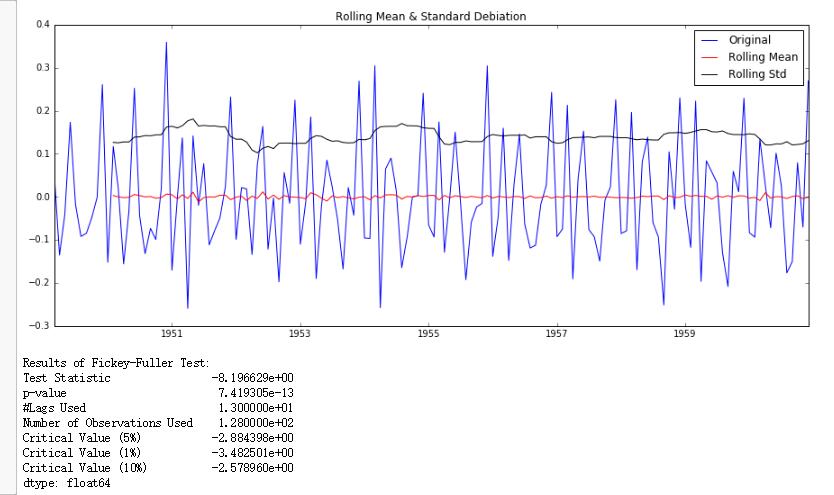
对二阶差分进行adf检验,可以看到,二阶差分,p值非常小,小于1%,检验统计量也明显小于%1的临界值。因此认定为很平稳.
分解
建立有关趋势和季节性的模型,并从模型中删除它们。
1 | #时间序列分解 |
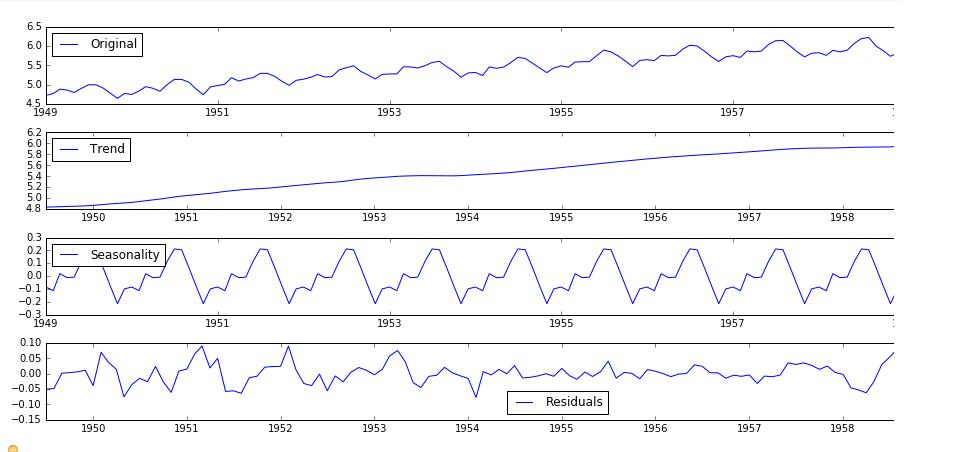
1 | #对残差进行ADF检验 |
对残差进行ADF检验,可以发现序列非常平稳。
时间序列建模
平稳性检验
平稳性检验的目的是为了判断序列是否平稳,如果不平稳,需要采取一定的措施进行平稳性处理,常见的方法是差分,我们需要选择合适的差分阶数。只要能够通过1%显著性检测,差分阶数就是合理的,我们希望阶数越小越好。
ADF检验
ADF检验前文已经说过,用于判断序列是否平稳。
自相关图和偏自相关图
前面我们对数据进行ADF检验,判断序列是否平稳,这里我们使用自相关图和偏自相关图对数据平稳性再次进行验证,一阶差分如下图:
1 | import statsmodels.api as sm |
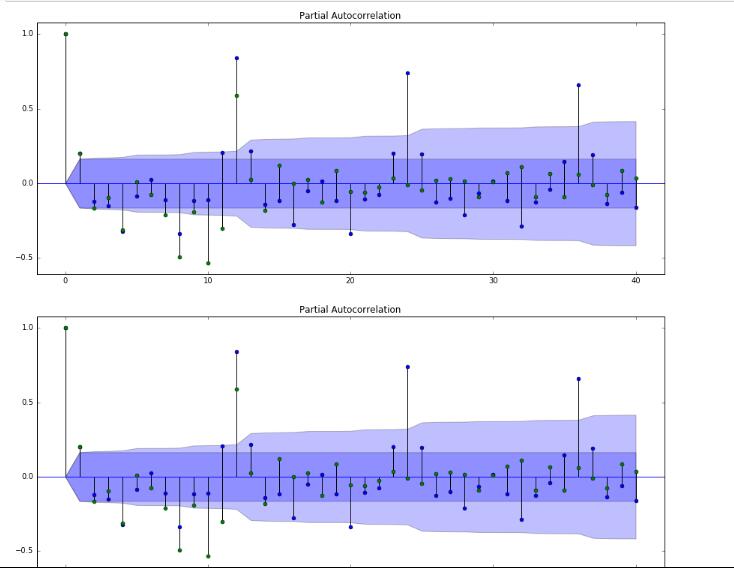
可以看出,一阶差分自相关和偏相系数拖尾特点明显。p=1,q=1
参数选择
差分阶数选择
我们发现,ARIMA该开源库,不支持3阶以上的差分。我们唯一的办法是先数据差分好,再传入模型进行建模。但是这样也带来了回退数据到原始序列数据的难度。
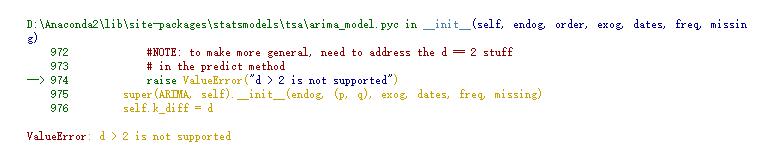
这里开发了差分和回退的方法如下:
1 | # 差分操作,d代表差分序列,比如[1,1,1]可以代表3阶差分。 [12,1]可以代表第一次差分偏移量是12,第二次差分偏移量是1 |
使用的时候,必须先调用diff_ts进行差分处理,然后进行建模,将预测数据传入predict_diff_recover方法进行还原。
1 | d=[1, 1] # 定义差分序列 |
差分阶数的选择通常越小越好,只要能够使得序列稳定就行。我们可以通过选择不同的阶数,然后进行平稳性检测,选择平稳性表现良好的阶数就行,一般一阶和二阶用的比较多。
p和q选择
差分阶数确定后,我们需要确定p和q. 对于个数不多的时序数据,我们可以通过观察自相关图和偏相关图来进行模型识别,倘若我们要分析的时序数据量较多,例如要预测每只股票的走势,我们就不可能逐个去调参了。这时我们可以依据BIC准则识别模型的p, q值,通常认为BIC值越小的模型相对更优。这里我简单介绍一下BIC准则,它综合考虑了残差大小和自变量的个数,残差越小BIC值越小,自变量个数越多BIC值越大。个人觉得BIC准则就是对模型过拟合设定了一个标准。当然,我们也可以使用AIC指标。
1 | #注意这里面使用的ts_log_diff是经过合适阶数的差分之后的数据,上文中提到ARIMA该开源库,不支持3阶以上的#差分。所以我们需要提前将数据差分好再传入 |
通过上述方法可以得到最优的p和q。
模型
我们使用一阶差分进行构建。
AR(p)模型
1 | # AR模型,q=0 |
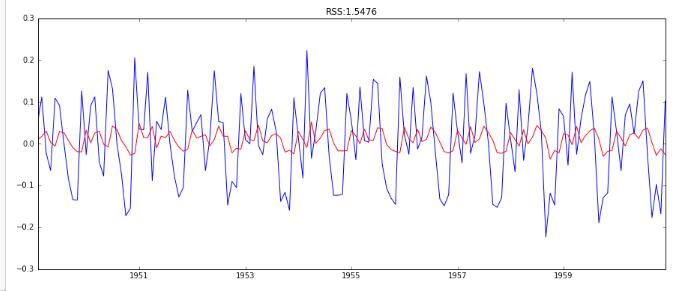
MA(q)模型
1 | #MA模型 p=0 |
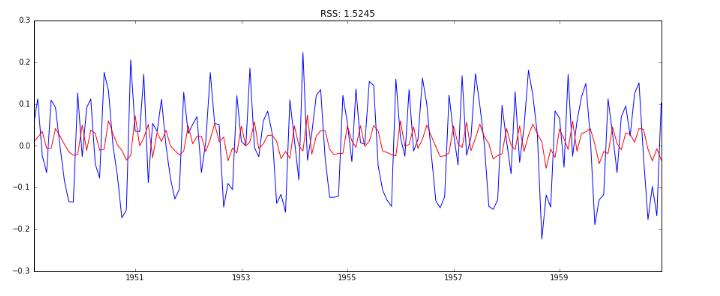
ARIMA(p,q)模型
1 | #ARIMA |
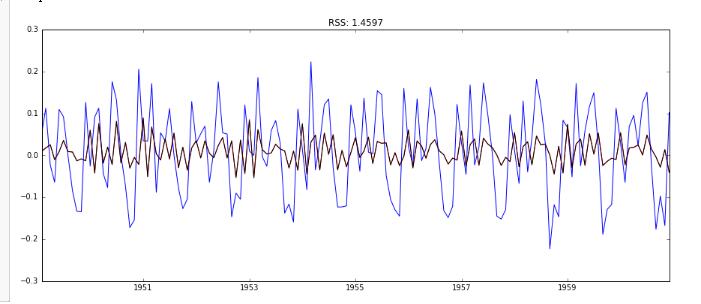
可以发现,ARIMA在AR和MA基础上,RSS有所减少,故模型有所提高。
我们使用上文中提高的p和q选择方法,对一阶差分结果进行p和q选择。
1 | _proper_model(ts_log_diff, 9) |
故可以使用p=8,q=7再次进行测试。得到如下结果:
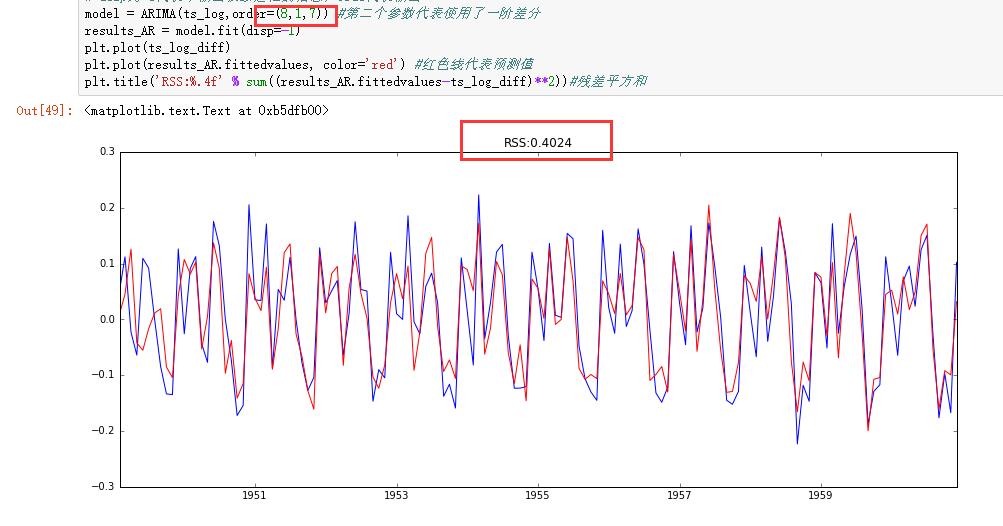
可以发现,残差平方和RSS已经优化到0.40了。
数据还原
1 | ts_log_diff = diff_ts(ts_log, d=[1])#调用差分方法,方便后续还原 |
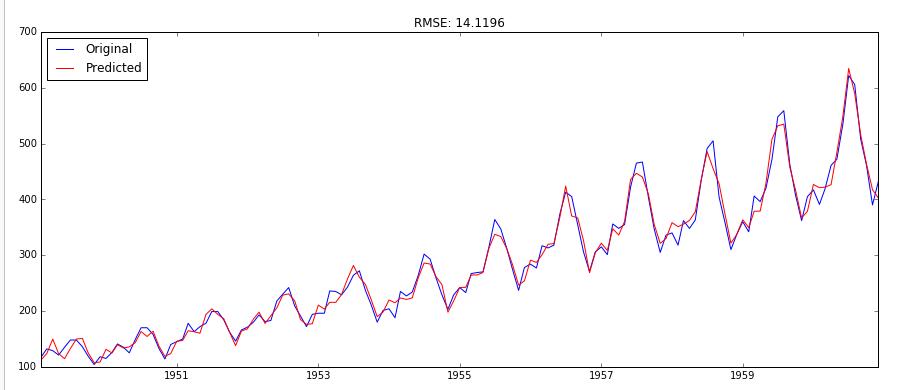
预测未来走势
使用forecast进行预测,参数为预测值个数。这个得到的就是进行自动差分还原后的数据,因为我们建立模型的时候ARIMA(p,1,q), 第二个参数就是差分阶数,forecast会将结果恢复回差分前的数据,因此我们直接将结果通过np.exp来恢复到最原始数据即可。但是ARIMA只支持最多2阶差分,因此我们可以使用ARMA模型,将我们手动差分完的数据传入。最后预测的时候,使用我们自定义的差分还原方法,对预测得到的值进行差分还原。
1 | # forecast方法会自动进行差分还原,当然仅限于支持的1阶和2阶差分 |
我们希望能够将预测的数据和原来的数据绘制在一起,为了实现这一目的,我们需要增加数据索引,使用开源库arrow:
1 | #定义获取连续时间,start是起始时间,limit是连续的天数,level可以是day,month,year |
1 | # 预测从1961-01-01开始,也就是我们训练数据最后一个数据的后一个日期 |
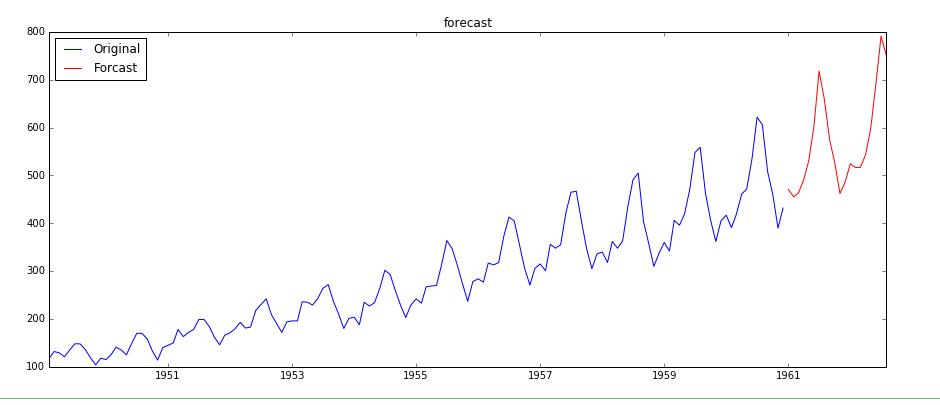
遗留问题:
如果直接将差分处理的结果传入ARMA模型,再进行forecast预测,如何对预测的结果进行还原至原始序列?
参考
Complete guide to create a Time Series Forecast (with Codes in Python)

