强化学习(Reinforcement Learning, RL)又叫做增强学习,是近年来机器学习和智能控制领域的主要方法之一。本文将重点介绍强化学习的概念以及马尔科夫决策过程。
引入
定义
英文定义:Reinforcement learning is learning what to do —-how to map situations to actions —- so as to maximize a numerical reward signal.
也就是说强化学习关注的是智能体如何在环境中采取一系列行为,从而获得最大的累积回报。通过强化学习,一个智能体应该知道在什么状态下应该采取什么行为。RL是从环境状态到动作的映射的学习,我们把这个映射称为策略。
举例
那么强化学习具体解决哪些问题呢,我们来举几个例子:
flappy bird 是现在很流行的一款小游戏,现在我们假设有一只机器小鸟,让它自行进行游戏,但是我们却没有小鸟的动力学模型,也不打算了解它的动力学。要怎么做呢? 这时就可以给它设计一个增强学习算法,然后让小鸟不断的进行游戏,如果小鸟撞到柱子了,那就获得-1的回报,否则获得0回报。通过这样的若干次训练,我们最终可以得到一只飞行技能高超的小鸟,它知道在什么情况下采取什么动作来躲避柱子。
假设我们要构建一个下国际象棋的机器,这种情况不能使用监督学习,首先,我们本身不是优秀的棋手,而请象棋老师来遍历每个状态下的最佳棋步则代价过于昂贵。其次,每个棋步好坏判断不是孤立的,要依赖于对手的选择和局势的变化。是一系列的棋步组成的策略决定了是否能赢得比赛。下棋过程的唯一的反馈是在最后赢得或是输掉棋局时才产生的。这种情况我们可以采用增强学习算法,通过不断的探索和试错学习,增强学习可以获得某种下棋的策略,并在每个状态下都选择最有可能获胜的棋步。目前这种算法已经在棋类游戏中得到了广泛应用。
强化学习和监督学习区别
可以看到,增强学习和监督学习的区别较大,在之前的讨论中,我们总是给定一个样本x,然后给或者不给\(label y\)。之后对样本进行拟合、分类、聚类或者降维等操作。然而对于很多序列决策或者控制问题,很难有这么规则的样本。比如,四足机器人的控制问题,刚开始都不知道应该让其动那条腿,在移动过程中,也不知道怎么让机器人自动找到合适的前进方向。另外如要设计一个下象棋的AI,每走一步实际上也是一个决策过程,虽然对于简单的棋有启发式方法,但在局势复杂时,仍然要让机器向后面多考虑几步后才能决定走哪一步比较好,因此需要更好的决策方法。
因此这里面主要的区别包括:
- 增强学习是试错学习(Trail-and-error),由于没有直接的指导信息,智能体要以不断与环境进行交互,通过试错的方式来获得最佳策略。
- 延迟回报,增强学习的指导信息很少,而且往往是在事后(最后一个状态)才给出的,这就导致了一个问题,就是获得正回报或者负回报以后,如何将回报分配给前面的状态。
思路
对于这种控制决策问题,有这么一种解决思路。我们设计一个回报函数(reward function),如果learning agent(如上面的四足机器人、象棋AI程序)在决定一步后,获得了较好的结果,那么我们给agent一些回报(比如回报函数结果为正),得到较差的结果,那么回报函数为负。比如,四足机器人,如果他向前走了一步(接近目标),那么回报函数为正,后退为负。如果我们能够对每一步进行评价,得到相应的回报函数,那么就好办了,我们只需要找到一条回报值最大的路径(每步的回报之和最大),就认为是最佳的路径。
增强学习是机器学习中一个非常活跃且有趣的领域,相比其他学习方法,增强学习更接近生物学习的本质,因此有望获得更高的智能。增强学习在很多领域已经获得成功应用,比如自动直升机,机器人控制,手机网络路由,市场决策,工业控制,高效网页索引等。特别是在棋类游戏中。Tesauro(1995)描述的TD-Gammon程序,使用增强学习成为了世界级的西洋双陆棋选手。这个程序经过150万个自生成的对弈训练后,已经近似达到了人类最佳选手的水平,并在和人类顶级高手的较量中取得40盘仅输1盘的好成绩。
接下来,先介绍一下马尔科夫决策过程(MDP,Markov decision processes)。
马尔科夫模型类型
大家应该还记得马尔科夫链(Markov Chain),了解机器学习的也都知道隐马尔可夫模型(Hidden Markov Model,HMM)。它们具有的一个共同性质就是马尔可夫性(无后效性),也就是指系统的下个状态只与当前状态信息有关,而与更早之前的状态无关。
马尔可夫决策过程(Markov Decision Process, MDP)也具有马尔可夫性,与上面不同的是MDP考虑了动作,即系统下个状态不仅和当前的状态有关,也和当前采取的动作有关。还是举下棋的例子,当我们在某个局面(状态s)走了一步(动作a),这时对手的选择(导致下个状态s’)我们是不能确定的,但是他的选择只和s和a有关,而不用考虑更早之前的状态和动作,即s’是根据s和a随机生成的。
我们用一个二维表格表示一下,各种马尔可夫子模型的关系就很清楚了:
马尔科夫决策过程
形式化定义
一个马尔科夫决策过程由一个五元组构成(\(S,A,\{P_{sa}\},\gamma,R\))
\(S\)表示状态集(states)。(比如,在自动直升机系统中,直升机当前位置坐标组成状态集)
\(A\)表示一组动作(actions)。(比如,使用控制杆操纵的直升机飞机方向,让其向前,向后蹬)
\(P_{sa}\)是状态转移概率。S中的一个状态到另一个状态的转变,需要A来参与。\(P_{sa}\)表示的是在当前\(s \in S\)状态下,经过\(a \in A\)作用后,会转移到的其他状态的概率分布情况(当前状态执行a后可能跳转到很多状态)。比如在状态\(s\)下执行动作\(a\),转移到\(s’\)的概率可以表示为\(P(s’|s,a)\)。
\(\gamma \in [0,1)\)是阻尼系数(discount factor)
\(R:S×A→\mathbb{R}\),R是回报函数(reward function),如果一组\((s,a)\)转移到了下个状态\(s’\),那么回报函数可记为\(R(s’|s,a)\)。回报函数经常写作S的函数(只与S有关),这样,R可重新写作\(R:S→\mathbb{R}\)。
MDP的动态过程如下:某个agent的初始状态为\(s_0\),然后从A中挑选一个动作\(a_0\),执行后,agent按\(P_{sa}\)概率随机转移到了下一个\(s_1\)状态,\(s_1 \in P_{s_0 a_0}\)。然后再执行一个动作\(a_1\),就转移到了\(s_2\),接下来再执行\(a_2\)…,我们可以用下面的图表示整个过程: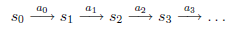
如果回报r是根据状态s和动作a得到的,则MDP还可以表示成下图: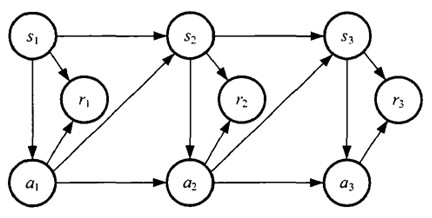
注意,上述挑选动作是有一定策略的,即从状态→动作的映射是需要根据一定的策略的,将会在下面阐述。而状态转移概率可能是模型的参数,需要从多种现成状态中进行学习得到。
我们定义经过上面转移路径后,得到的回报函数之和如下:
$$R(s_0,a_0)+\gamma R(s_1,a_1)+\gamma^2 R(s_2,a_2) + \ldots$$
如果R只和S有关,那么上式可以写作:
$$R(s_0)+\gamma R(s_1)+\gamma^2 R(s_2) + \ldots$$
我们的目标是选择一组最佳的Action,使得全部的回报加权和期望最大。
$$\max E[R(s_0)+\gamma R(s_1)+\gamma^2 R(s_2) + \ldots]$$
从上式可以发现,在t时刻的回报值被打了\(\gamma^t\)的折扣,是一个逐步衰减的过程,越靠后的状态对回报和影响越小。最大化期望值也就是要将大的\(R(s_i)\)尽量放到前面,小的尽量放到后面。
策略
已经处于某个状态s时,我们会以一定的策略\(\pi\)来选择下一个动作a执行,然后转换到另一个状态\(s’\)。我们将这个动作的选择过程称为策略(policy),每一个policy其实就是一个状态到动作的映射函数\(\pi:S→A\)。给定\(\pi\)也就是给定了\(a=\pi(s)\),也就是说,知道了\(\pi\)就知道了每个状态下一步应该执行的动作。
值函数
上面我们提到增强学习学到的是一个从环境状态到动作的映射(即行为策略),记为策略\(\pi: S→A\)。而增强学习往往又具有延迟回报的特点: 如果在第n步输掉了棋,那么只有状态\(s_n\)和动作\(a_n\)获得了立即回报\(R(s_n,a_n)=-1\),前面的所有状态立即回报均为0。所以对于之前的任意状态s和动作a,立即回报函数\(R(s,a)\)无法说明策略的好坏。因而需要定义值函数(value function,又叫效用函数)来表明当前状态下策略\(\pi\)的长期影响。值函数又称作折算累积回报(discounted cumulative reward)。
用\(V^{\pi}(s)\)表示在策略\(\pi\)下,状态s的值函数。\(R_i\)表示未来第i步的立即回报,常见的值函数有以下三种:
$$a) \ V^{\pi}(s)=E_{\pi}\left[\sum_{i=0}^h R_i| s_0=s \right]$$
$$b) \ V^{\pi}(s)= lim_{h→ \infty}E_{\pi}\left[\frac{1}{h}\sum_{i=0}^h R_i| s_0=s \right]$$
$$c) \ V^{\pi}(s)=E_{\pi}\left[\sum_{i=0}^{\infty} \gamma^i R_i | s_0=s \right]$$
其中,
a)是采用策略\(\pi\)的情况下未来有限h步的期望立即回报总和;
b)是采用策略\(\pi\)的情况下期望的平均回报;
c)是值函数最常见的形式,式中\(γ∈[0,1]\)称为折合因子,表明了未来的回报相对于当前回报的重要程度。特别的,\(γ=0\)时,相当于只考虑立即,不考虑长期回报,\(γ=1\)时,将长期回报和立即回报看得同等重要。接下来我们只讨论第三种形式。
现在将值函数的第三种形式展开,其中\(R_i\)表示未来第i步回报,\(s’\)表示下一步状态,则有:
$$V^{\pi}(s)=E_{\pi}[R_0+\gamma R_1 + \gamma^2 R_2 + \gamma^3 R_3 + \ldots|s_0=s,\pi] \\\\
=E_{\pi}[R_0+\gamma E[R_1+\gamma R_2 + \gamma^2 R_3 + \ldots]|s_0=s,\pi] \\\\
=E_{\pi}[R_0+\gamma V^{\pi}(s’)]$$
给定策略\(\pi\)和初始状态\(s_0\),则动作\(a_0=\pi(s_0)\),\(a_0\)在\(\pi\)给定下是唯一的。但下个时刻将以概率\(p(s’|s_0,a_0)\)转向下个状态\(s’\),也就是说A→S可能有多种,根据Bellman等式,得到:
$$V^{\pi}(s)=R(s)+\gamma \sum_{s’ \in S} P_{s \pi(s)}(s’)V^{\pi}(s’)$$
\(s’\)表示下一个状态。前面R(s)称为立即回报(immediate reward),就是R(当前状态)。第二项也可以写作\(E_{s’ \sim P_{s\pi(s)}(s)}[V^{\pi}(s’)]\),是下一状态值函数的期望值,下一状态s’符合\(P_{s\pi(s)}\)分布。
当状态个数有限时,可以通过上式求出每一个s的V。如果列出线性方程组的话,也就是|S|个方差,|S|个未知数,直接求解即可。
我们求V的目的是想寻找一个当前状态s下,最优的行动策略\(\pi\),定义最优的\(V^{*}\)如下:
$$V^{*}(s)=\max_{\pi} V^{\pi} (s)$$
就是从可选的策略\(\pi\)中挑选一个最优策略(discounted rewards最大)。
上式的Bellman等式形式如下:
$$V^{*}(s)=R(s)+\max_{a \in A} \gamma \sum_{s’ \in S} P_{sa}(s’)V^{*}(s’)$$
第一项与\(\pi\)无关,所以不变。第二项是一个\(\pi\)就决定了每个状态s的下一步动作a,执行a后,s’按概率分布的回报概率和的期望。可根据下图进行理解。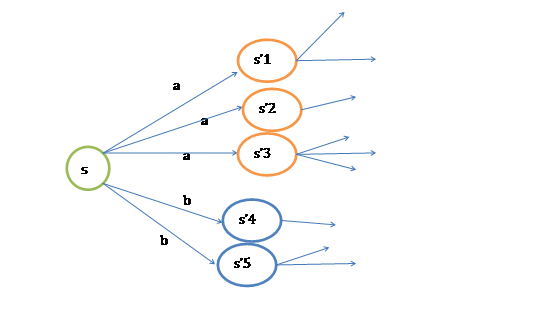
定义了最优的\(V^{*}\),我们再定义最优的策略\(\pi^{*}:S→A\)如下:
$$\pi^{*}(s)=arg \max_{a \in A} \sum_{s’ \in S}P_{sa}(s’)V^{*}(s’)$$
选择最优的\(\pi^{*}\),也就确定了每个状态s的下一步最优动作a。
根据以上式子,我们可以知道:
$$V^{*}(s)=V^{\pi^{*}}(s) \geq V^{\pi}(s)$$
上式意思就当前状态的最优值函数\(V^{*}\),是由采用最优执行策略\(\pi^{*}\)的情况下得出的,采用最优执行方案的回报显然要比采用其他的执行策略\(\pi\)要好。
这里需要注意的是,如果我们能够求得每个s下最优的a,那么从全局来看,\(S→A\),而生成的这个映射是最优映射,称为\(\pi^{*}\)。\(\pi^{*}\)针对全局的s,确定了每一个s的下一个动作a,不会因为初始状态s选取的不同而不同。
值迭代和策略迭代法
上节我们给出了迭代公式和优化目标,这节讨论两种求解有限状态MDP具体策略的有效算法。这里,我们只针对MDP是有限状态、有限动作的情况。
值迭代法
1)将每个s的V(s)初始化为0
2)循环直到收敛{
对于每一个状态s,对V(s)做更新
\(V(s):=R(s)+\max_{a \in A} \gamma \sum_{s’}P_{sa}(s’)V(s’)\)
}
内循环的实现由两种策略。
1. 同步迭代法
拿初始化后的第一次迭代来说吧,初始状态所有的V(s)都为0。然后对所有的s都计算新的\(V(s)=R(s)+0=R(s)\)。在计算每一个状态时,得到新的V(s)后,先存下来,不立即更新。待所有的s的新值V(s)都计算完毕后,再统一更新。
2. 异步迭代法
与同步迭代对应的就是异步迭代了,对每一个状态s,得到新的\(V(s)\)后,不存储,直接更新。这样,第一次迭代后,大部分\(V(s)>R(s)\)。
不管使用这两种的哪一种,最终V(s)会收敛到\(V^{*}(s)\)。知道了\(V^{*}\)后,我们再使用公式(3)来求出相应的最优策略\(\pi^{*}\),当然\(\pi^{*}\)可以在求\(V^{*}\)的过程中求出。
策略迭代法
值迭代法使V值收敛到\(V^{*}\),而策略迭代法关注\(\pi\),使\(\pi\)收敛到\(\pi^{*}\)。
1) 将随机指定一个S到A的映射\(\pi\)。
2) 循环知道收敛{
a) 令\(V:=V^{\pi}\)
b) 对于每一个状态s,对\(\pi(s)\)做更新。
\(\pi(s):=arg \max_{a \in A} \sum_{s’} P_{sa}(s’)V(s’)\)
}
a)步中的V可以通过之前的Bellman等式求出:
$$V^{\pi}(s)=R(s)+\gamma \sum_{s’ \in S} P_{s\pi(s)}(s’)V^{\pi}(s’)$$
这一步会求得所有状态s的\(V^{\pi}(s)\)。
b)步实际上就是根据a步的结果挑选出当前状态s下,最优的a,然后对\(\pi(s)\)做更新。
对于值迭代和策略迭代很难说哪种方法好,哪种不好。对于规模比较小的MDP来说,策略一般能够更快地收敛。但是对于规模很大(状态很多)的MDP来说,值迭代比较容易(不用求线性方程组)。
MDP中的参数估计
在之前讨论的MDP中,我们是已知状态转移概率\(P_{sa}\)和回报函数\(R(s)\)的。但在很多实际问题中,这些参数不能显式得到,我们需要从数据中估计出这些参数(通常S、A和\(\gamma\)是已知的)。
假设我们已知很多条状态转移路径如下: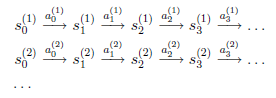
其中,\(s_i^{(j)}\)是i时刻,第j条转移路径对应的状态,\(a_i^{(j)}\)是\(s_i^{(j)}\)状态时要执行的动作。每个转移路径中状态数是有限的,在实际操作过程中,每个转移链要么进入终结状态,要么达到规定的步数就会终结。
如果我们获得了很多上面类似的转移链(相当于有了样本),那么我们就可以使用最大似然估计来估计状态转移概率。
$$P_{sa}(s’)=\frac{times \ took \ we \ action \ a \ in \ state \ s \ and \ got \ to \ s’}{times \ we \ took \ action \ a \ in \ state \ s}$$
分子是从s状态执行动作a后到达s’的次数,分母是在状态s时,执行a的次数。两者相除就是在s状态下执行a后,会转移到s’的概率。
为了避免分母为0的情况,我们需要做平滑。如果分母为0,则令\(P_{sa}(s’)=\frac{1}{|S|}\),也就是说当样本中没有出现过在s状态下执行a的样例时,我们认为转移概率均分。
上面这种估计方法是从历史数据中估计,这个公式同样适用于在线更新。比如我们新得到了一些转移路径,那么对上面的公式进行分子分母的修正(加上新得到的count)即可。修正过后,转移概率有所改变,按照改变后的概率,可能出现更多的新的转移路径,这样\(P_{sa}\)会越来越准。
同样,如果回报函数未知,那么我们认为R(s)为在s状态下已经观测到的回报均值。
当转移概率和回报函数估计出之后,我们可以使用值迭代或者策略迭代来解决MDP问题。比如,我们将参数估计和值迭代结合起来(在不知道状态转移概率情况下)的流程如下:
1、 随机初始化\(\pi\)
2、 循环直到收敛 {
(a) 在样本上统计\(\pi\)中每个状态转移次数,用来更新\(P_{sa}\)和R
(b) 使用估计到的参数来更新V(使用上节的值迭代方法)
(c) 根据更新的V来重新得出\(\pi\)
}
在(b)步中我们要做值更新,也是一个循环迭代的过程,在上节中,我们通过将V初始化为0,然后进行迭代来求解V。嵌套到上面的过程后,如果每次初始化V为0,然后迭代更新,就会很慢。一个加快速度的方法是每次将V初始化为上一次大循环中得到的V。也就是说V的初值衔接了上次的结果。
至此我们了解了马尔可夫决策过程在强化学习中的应用。

