蘑菇先生学习记

卷积神经网络实践

发表于 | 分类于 | 阅读量

　　本文将介绍使用Python书写“卷积神经网络”代码的具体步骤和细节，本文会采用Python开源库Theano，Theano封装了卷积等操作，使用起来比较方便。具体代码可参考神经网络和深度学习教程。在本文中，卷积神经网络对MNIST手写数字的预测性能，测试集准确率可以达到99.30%。

Theano安装

Anaconda

　　Theano依赖于numpy等库，故首先安装集成包Anaconda，这个软件内嵌了python，并且还包含了很多用于计算的库。本文使用的是4.3.24版本，内置python为2.7.13版本。下载地址为：https://www.continuum.io/downloads

MinGW

　　Theano底层依赖于C编译器。一种方式是，在控制台输入conda install mingw libpython即可。注意libpython也必须要安装，否则后面导入theano后会报“no module named gof”的错误。另一种也可以手动去MinGW安装包安装，但libpython仍然需要安装。

Theano

　　最后安装Theano，使用pip install theano即可。

数据集加载

　　本文使用的数据集同样是来自MNIST手写数字库。

1
2
3
4
5
6
7
8
9
10
11
def  load_data_shared(filename="../data/mnist.pkl.gz"):
    f = gzip.open(filename, 'rb')
    training_data, validation_data, test_data = cPickle.load(f)
    f.close()
    def shared(data):
        shared_x = theano.shared(
            np.asarray(data[0], dtype=theano.config.floatX), borrow=True)
        shared_y = theano.shared(
            np.asarray(data[1], dtype=theano.config.floatX), borrow=True)
        return shared_x, T.cast(shared_y, "int32")
    return [shared(training_data), shared(validation_data), shared(test_data)]

　　这里使用了theano的shared变量，shared变量意味着shared_x和shared_y可以在不同的函数中共享。在使用GPU时，Theano能够很方便的拷贝数据到不同的GPU中。borrow=True代表了浅拷贝。

卷积神经网络结构

　　本文采取的神经网络结构如下: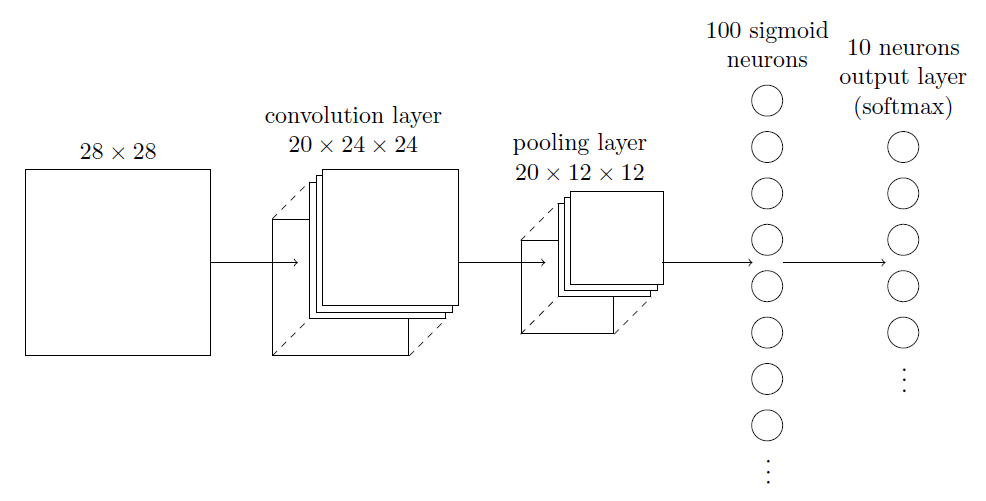
cnn
　　输入层是5万条手写数字图像，每条数据是28*28的像素矩阵。然后在右边插入一个卷积层，使用5*5的局部感受野，跨距为1，20个特征映射对输入层进行特征提取。因此得到20*(28-5+1)*(28-5+1)=20*24*24规格的卷积层，这意味着每一副图像经过特征映射后都会得到20副24*24的卷积结果图像。接着再插入一个最大值混合层，使用2*2的混合窗口来合并特征。因此得到规格为20*(24/2)*(24/2)=20*12*12规格的混合层。紧接着再插入一个全连接层，有100个神经元。最后是输出层，和全连接层采用全连接的方式，这里使用柔性最大值来求得激活值。

运行代码

　　让我们先总体看一下最终运行的代码：

1
2
3
4
5
training_data,validation_data,test_data=load_data_shared()
mini_batch_size= 10
net2 = Network([ConvPoolLayer(image_shape=(mini_batch_size,1,28,28),filter_shape=(20,1,5,5),poolsize=(2,2)),
               FullyConnectedLayer(n_in=20*12*12,n_out=100),SoftmaxLayer(n_in=100,n_out=10)],mini_batch_size)
net2.SGD(training_data,60,mini_batch_size,0.1,validation_data,test_data)

　　可以看到运行的代码包括加载数据集、构建神经网络结构、运行学习算法SGD。下面将介绍不同层的代码细节。

卷积层和混合层

　　下面将描述运行代码中的细节。首先介绍卷积层和混合层的代码。这里面将卷积层和混合层统一封装，使得代码更加紧凑。首先看一下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class ConvPoolLayer(object):
    """Used to create a combination of a convolutional and a max-pooling
    layer.  A more sophisticated implementation would separate the
    two, but for our purposes we'll always use them together, and it
    simplifies the code, so it makes sense to combine them.
    """
    def __init__(self, filter_shape, image_shape, poolsize=(2, 2),
                 activation_fn=sigmoid):
        """`filter_shape` is a tuple of length 4, whose entries are the number
        of filters, the number of input feature maps, the filter height, and the
        filter width.

        `image_shape` is a tuple of length 4, whose entries are the
        mini-batch size, the number of input feature maps, the image
        height, and the image width.

        `poolsize` is a tuple of length 2, whose entries are the y and
        x pooling sizes.

        """
        self.filter_shape = filter_shape
        self.image_shape = image_shape
        self.poolsize = poolsize
        self.activation_fn=activation_fn
        # initialize weights and biases
        n_out = (filter_shape[0]*np.prod(filter_shape[2:])/np.prod(poolsize))
        self.w = theano.shared(
            np.asarray(
                np.random.normal(loc=0, scale=np.sqrt(1.0/n_out), size=filter_shape),
                dtype=theano.config.floatX),
            borrow=True)
        self.b = theano.shared(
            np.asarray(
                np.random.normal(loc=0, scale=1.0, size=(filter_shape[0],)),
                dtype=theano.config.floatX),
            borrow=True)
        self.params = [self.w, self.b]

    def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
        self.inpt = inpt.reshape(self.image_shape)
        conv_out = conv.conv2d(
            input=self.inpt, filters=self.w, filter_shape=self.filter_shape,
            image_shape=self.image_shape)
        pooled_out = pool.pool_2d(
            input=conv_out, ds=self.poolsize, ignore_border=True)
        self.output = self.activation_fn(
            pooled_out + self.b.dimshuffle('x', 0, 'x', 'x'))
        self.output_dropout = self.output # no dropout in the convolutional layers

初始化　　

　　首先看一下初始化方法。其中参数filter_shape是一个四元组，由卷积核(filter)个数、输入特征集(input feature maps)个数、卷积核行数、卷积核的列数构成。这里的滤波器个数对应的是前面图中的20，也就是使用20个卷积核进行特征提取。行数和列数大小也就是局部感受野的大小。而输入特征集个数代表的是输入数据，例如一般图都有3个通道Channel，每个图初始有3张feature map(R,G,B)，对于一张图，其所有feature map用一个filter卷成一张feature map。用20个filter，则卷成20张feature map。本文的数据使用的是手写图像的灰度值，因此只有1个feature map。image_shape参数也是一个四元组，由随机梯度下降选择的样本量mini_batch_size，输入特征集个数，每张图的宽度和高度构成。poolsize是卷积层到混合层使用的混合窗口大小。
　　首先进行参数的保存，前面的层使用的是sigmoid激活函数。n_out在初始化权重的时候指定方差使用，在本文中n_out=125,具体该数值含义目前不是非常理解。np.random.normal(loc=0, scale=np.sqrt(1.0/n_out), size=filter_shape使用高斯分布初始化了一个四维数组，规格为(20L,1L,5L,5L),由于一个特征映射有5*5=25个参数，则20个特征映射
就有500个权重参数。np.random.normal(loc=0, scale=1.0, size=(filter_shape0,))初始化偏置值，每个特征映射只需要对应1个偏置，20个特征映射需要20个偏置即可。可以看出这里的参数个数总共有520个。如果不使用共享权重的方式，而是使用全连接的话，若隐藏层有30个神经元，则有784*30+30=23550个参数，几乎比卷积层多了40倍的参数。使用shared变量包装w和b后，w就是一个TensorType类型的变量,b是一个TensorType变量。

卷积操作

　　set_inpt方法会根据参数来计算当前层的输出。参数inpt是前一层的输出，参数inpt_dropout是经过弃权策略后的前一层的输出。self.inpt = inpt.reshape(self.image_shape)将输入数据按照(10L,1L,28L,28L)的规格进行重塑。10代表每个小批量有10条数据，1L代表只有1个输入特征集，28*28则代表图像的大小。
　　接着是卷积操作：

1
conv_out = conv.conv2d(input=self.inpt, filters=self.w, filter_shape=self.filter_shape,image_shape=self.image_shape)

　　使用的是theano.tensor.nnet.conv封装好的conv2d卷积操作方法。对于该方法的理解，下面通过一个例子来理解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
import numpy as np
import theano
import theano.tensor as T
from theano import function
from theano.tensor.nnet.conv import conv2d

inputs = T.tensor4(name='input', dtype='float64')#输入时一个4维向量，[图片数量，RGB通道数，图片行数，图片列数]

#w_shp = (2, 2, 1, 2) # [卷积核数量，输入特征通道数，卷积核行数，卷积核列数]
W = theano.shared(
    np.asarray(
        [
            [[[1., 1.]],
             [[1., 1.]]],
            [[[2., 2.]],
             [[1., 1.]]]
        ],
        dtype=inputs.dtype),
    name='W')#第一维代表卷积核，第二维对应通道，每种通道都有相对应的权重

conv_out = conv2d(inputs, W)# 卷积操作

f = theano.function([inputs], conv_out)

#img_shp = [1,2,1,5] #[多少张图片，RGB通道数，图片行数，图片列数]
i = np.asarray([
    [[[1., 2., 3., 4., 5.]],
     [[1., 2., 3., 4., 5.]]]
], dtype='float64') #只输入1张图片
ii = f(i)
print(i.shape)
print(W.get_value().shape)
print(ii)
print(ii.shape)

# out result:
(1L, 2L, 1L, 5L)
(2L, 2L, 1L, 2L)
[[[[  6.  10.  14.  18.]]

  [[  9.  15.  21.  27.]]]]
(1L, 2L, 1L, 4L)

　　上述使用两个卷积核，因此对于每幅图，有两个输出。对于第一个卷积结果[ 6. 10. 14. 18.]，是如下计算得到的：
　　利用第一个卷积核前半部分[1,1]扫描第一个通道数据，根据线性组合\(wx+b\)，得到[1*1+1*2,1*2+1*3,1*3+1*4,1*4+1*5]=[3,5,7,9]；同理利用第一个卷积核后半部分[1,1]扫描得到[3,5,7,9];两个向量相加得到[6. 10. 14. 18.]
　　同样，对于第二个卷积结果[ 9. 15. 21. 27.]。利用第二个卷积核扫描两个通道的数据，再相加即可得到。

池化操作

1
2
pooled_out = pool.pool_2d(
            input=conv_out, ds=self.poolsize, ignore_border=True,mode='max')

　　对卷积结果进行池化。这里使用的是最大池化(混合)方法。使用poolsize大小的窗口扫描卷积后的结果，取poolsize范围内的最大值作为结果。我们可以把最大值混合看作一种网络询问是否有一个给定的特征在一个图像区域中。然后扔掉确切的位置信息。直观上，一旦一个特征被发现，它的确切位置并不如它相对于其它特征的位置重要。同时这有助于减少在以后的层所需的参数的数目。

激活操作　

　　接着使用激活函数来求得输出。由于池化后的结果仍然是四维的TensorType，b的结构是TensorType,因此我们需要调整b的结构为4维。这里使用dimshuffle，它是用来改变一个数组张量结构的一个工具，我们需要利用这个工具将b张成4维结构。

1
2
self.output = self.activation_fn(
            pooled_out + self.b.dimshuffle('x', 0, 'x', 'x'))

　　上式dimshuffle的参数可以’0，1或’x’。0代表原始的行数，1代表原始的列数，x代表增加1维。因此张量后的b为(1L,20L,1L,1L)。

全连接层

　　全连接层和之前讨论前馈神经网络中的隐藏层类似。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class FullyConnectedLayer(object):

    def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0):
        self.n_in = n_in
        self.n_out = n_out
        self.activation_fn = activation_fn
        self.p_dropout = p_dropout
        # Initialize weights and biases
        self.w = theano.shared(
            np.asarray(
                np.random.normal(
                    loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)),
                dtype=theano.config.floatX),
            name='w', borrow=True)
        self.b = theano.shared(
            np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)),
                       dtype=theano.config.floatX),
            name='b', borrow=True)
        self.params = [self.w, self.b]

    def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
        self.inpt = inpt.reshape((mini_batch_size, self.n_in))
        self.output = self.activation_fn(
            (1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
        self.y_out = T.argmax(self.output, axis=1)
        self.inpt_dropout = dropout_layer(
            inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
        self.output_dropout = self.activation_fn(
            T.dot(self.inpt_dropout, self.w) + self.b)

    def accuracy(self, y):
        "Return the accuracy for the mini-batch."
        return T.mean(T.eq(y, self.y_out))

初始化　

　　初始化参数包括该层神经元个数和后一层神经元个数。该层神经元个数n_in=20*12*12=2880,下一层神经元个数n_out=100。因此共有2880*100+100=288100个参数。这里激活函数仍然使用sigmoid。p_dropout指定了弃权概率，是为了防止过拟合。

dropout弃权

　　首先按照(mini_batch_size, self.n_in)调整输入结构，再计算激活值，计算激活值时使用到了弃权策略。弃权策略是为了防止过拟合，对于神经网络单元，按照一定的概率将其暂时从网络中丢弃。注意是暂时，对于随机梯度下降来说，由于是随机丢弃，故而每一个mini-batch都在训练不同的网络。具体过程如下所示：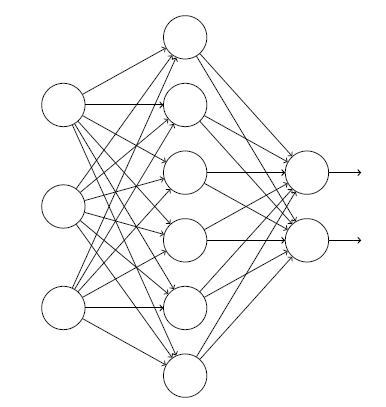
cnn
　　这是原始的结构。特别地，假设我们有一个训练数据x和对应的目标输出y。通常我们会通过在网络中前向传播x，然后进行反向传播来确定对梯度的贡献。使用弃权技术，这个过程就改了。我们会随机（临时）地删除网络中部分的隐藏神经元，输入层和输出层的神经元保持不变。在此之后，我们会得到最终如下线条所示的网络。注意那些被弃权的神经元，即那些临时被删除的神经元，用虚圈表示在图中：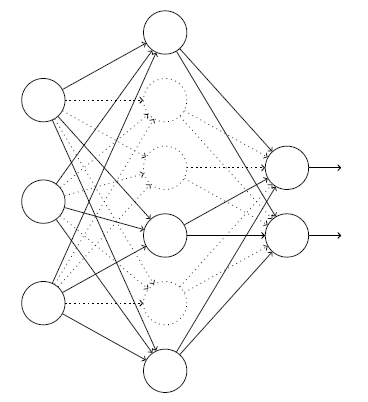
cnn
　　具体关于dropout的理解可参考理解dropout。
　　代码中的self.output和self.output_dropout是有区别的。
　　self.output是在测试阶段使用的，计算时需要乘以(1-self.p_dropout)。即在网络前向传播到输出层前时隐含层节点的输出值都要缩减到（1-v）倍。例如正常的隐层输出为a，此时需要缩减为a（1-v）。这里我的解释是：假设比例v=0.5，即在训练阶段，以0.5的比例忽略隐层节点；那么假设隐层有80个节点，每个节点输出值为1，那么此时只有40个节点正常工作；也就是说总的输出为40个1和40个0；输出总和为40；而在测试阶段，由于我们的权值已经训练完成，此时就不在按照0.5的比例忽略隐层输出，假设此时每个隐层的输出还是1，那么此时总的输出为80个1，明显比dropout训练时输出大一倍（由于dropout比例为0.5）；所以为了得到和训练时一样的输出结果，就缩减隐层输出为a（1-v）；即此时输出80个0.5，总和也为40.这样就使得测试阶段和训练阶段的输出“一致”了。可参考机器学习——Dropout原理介绍中测试阶段一节。
　　而self.output_dropout是在训练阶段使用的。self.output_dropout的计算是根据上述dropout定义来做的。使用伯努利分布生成掩码,来随机忽略部分神经元。公式参考如下：
cnn
　　具体代码如下：

1
2
3
4
5
def dropout_layer(layer, p_dropout):
       srng = shared_randomstreams.RandomStreams(
           np.random.RandomState(0).randint(999999))
       mask = srng.binomial(n=1, p=1-p_dropout, size=layer.shape)
       return layer*T.cast(mask, theano.config.floatX)

　　另外，还有一个问题，为什么只对全连接层应用弃权？
　　原则上我们可以在卷积层上应用一个类似的程序。但是，实际上那没必要：卷积层有相当大的先天的对于过度拟合的抵抗。原因是共享权重意味着卷积核被强制从整个图像中学习。这使他们不太可能去选择在训练数据中的局部特质。于是就很少有必要来应用其它规范化，例如弃权。

输出层

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class SoftmaxLayer(object):

    def __init__(self, n_in, n_out, p_dropout=0.0):
        self.n_in = n_in
        self.n_out = n_out
        self.p_dropout = p_dropout
        # Initialize weights and biases
        self.w = theano.shared(
            np.zeros((n_in, n_out), dtype=theano.config.floatX),
            name='w', borrow=True)
        self.b = theano.shared(
            np.zeros((n_out,), dtype=theano.config.floatX),
            name='b', borrow=True)
        self.params = [self.w, self.b]

    def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
        self.inpt = inpt.reshape((mini_batch_size, self.n_in))
        self.output = softmax((1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
        self.y_out = T.argmax(self.output, axis=1)
        self.inpt_dropout = dropout_layer(
            inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
        self.output_dropout = softmax(T.dot(self.inpt_dropout, self.w) + self.b)

    def cost(self, net):
        "Return the log-likelihood cost."
        return -T.mean(T.log(self.output_dropout)[T.arange(net.y.shape[0]), net.y])

    def accuracy(self, y):
        "Return the accuracy for the mini-batch."
        return T.mean(T.eq(y, self.y_out))

　　输出层和全连接层大同小异。主要区别包括，使用softmax激活函数代替sigmoid以及使用对数似然代价函数代替交叉熵代价函数。

柔性最大值

　　柔性最大值公式如下：
$$a_j^L = \frac{e^{z_j^L}}{\sum_k e^{z_k^L}}$$
　　同时有：
$$\sum_j a_j^L = \frac{\sum_j e^{z_j^L}}{\sum_k e^{z_k^L}}=1$$
　　因此柔性最大值层的输出可以看作是一个概率分布。在MNIST分类问题中，可以将\(a_j^L\)理解为网络估计正确数字分类为\(j\)的概率。

对数似然代价函数

　　前面说到可以把柔性最大值的输出看作是一个概率分布，因此我们可以使用对数似然代价函数。根据：
$$\mathcal{L} (\theta=\{W,b\}, \mathcal{D}) = \sum_{i=0}^{|\mathcal{D}|} \log(P(Y=y^{(i)}|x^{(i)}, W,b)) \\\ \ell (\theta=\{W,b\}, \mathcal{D}) = - \mathcal{L} (\theta=\{W,b\}, \mathcal{D})$$
　　具体代码：

1
2
3
4
5
loss = -T.mean(T.log(p_y_given_x)[T.arange(y.shape[0]), y])
# note on syntax: T.arange(y.shape[0]) is a vector of integers [0,1,2,...,len(y)].
# Indexing a matrix M by the two vectors [0,1,...,K], [a,b,...,k] returns the
# elements M[0,a], M[1,b], ..., M[K,k] as a vector.  Here, we use this
# syntax to retrieve the log-probability of the correct labels, y.

　　具体解释可参考上述注释部分。每次求得是一个mini-batch-size里的总代价。y的索引不一定是从0开始，因此使用[T.arange(y.shape[0]), y]来索引。
　　注意每次计算代价的时候，需要用到self.output_dropout，而self.output_dropout是在set_inpt定义的，cost和self.output_dropout都是预定义的符号运算，实际上每次计算代价时，都会进行前向传播计算出self.output_dropout。

Network初始化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Network(object):

    def __init__(self, layers, mini_batch_size):
        """Takes a list of `layers`, describing the network architecture, and
        a value for the `mini_batch_size` to be used during training
        by stochastic gradient descent.

        """
        self.layers = layers
        self.mini_batch_size = mini_batch_size
        self.params = [param for layer in self.layers for param in layer.params]
        self.x = T.matrix("x")
        self.y = T.ivector("y")
        init_layer = self.layers[0]
        init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
        for j in xrange(1, len(self.layers)):
            prev_layer, layer  = self.layers[j-1], self.layers[j]
            layer.set_inpt(
                prev_layer.output, prev_layer.output_dropout, self.mini_batch_size)
        self.output = self.layers[-1].output
        self.output_dropout = self.layers[-1].output_dropout

　　self.x定义了数据的符号化矩阵，参数是名称；self.y定义了分类的符号化向量，参数同样是名称。接着定义符号化前向传播算法，来计算输出。实际上初始化的时候，没有代入具体实际数据来进行前向传播计算输出，而是定义了前向传播计算图，后面层的输入依赖于前面层的前向传播输出，这样后面计算某一层的输出时，直接调用该层的输出符号，即可自动根据计算图去计算出前面层的输出结果。

学习算法

　　最后，让我们关注下核心的学习算法SGD。这里面还会介绍theano符号化计算,Theano会将符号数学化计算表示成graph,之后实际运行时才开始真正的计算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
def SGD(self, training_data, epochs, mini_batch_size, eta,
        validation_data, test_data, lmbda=0.0):
    """Train the network using mini-batch stochastic gradient descent."""
    training_x, training_y = training_data
    validation_x, validation_y = validation_data
    test_x, test_y = test_data

    # compute number of minibatches for training, validation and testing
    num_training_batches = size(training_data)/mini_batch_size
    num_validation_batches = size(validation_data)/mini_batch_size
    num_test_batches = size(test_data)/mini_batch_size

    # define the (regularized) cost function, symbolic gradients, and updates
    l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
    cost = self.layers[-1].cost(self)+\
           0.5*lmbda*l2_norm_squared/num_training_batches
    grads = T.grad(cost, self.params)
    updates = [(param, param-eta*grad)
               for param, grad in zip(self.params, grads)]

    # define functions to train a mini-batch, and to compute the
    # accuracy in validation and test mini-batches.
    i = T.lscalar() # mini-batch index
    train_mb = theano.function(
        [i], cost, updates=updates,
        givens={
            self.x:
            training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
            self.y:
            training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
        })
    validate_mb_accuracy = theano.function(
        [i], self.layers[-1].accuracy(self.y),
        givens={
            self.x:
            validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
            self.y:
            validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
        })
    test_mb_accuracy = theano.function(
        [i], self.layers[-1].accuracy(self.y),
        givens={
            self.x:
            test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
            self.y:
            test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
        })
    self.test_mb_predictions = theano.function(
        [i], self.layers[-1].y_out,
        givens={
            self.x:
            test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
        })
    # Do the actual training
    best_validation_accuracy = 0.0
    for epoch in xrange(epochs):
        for minibatch_index in xrange(num_training_batches):
            iteration = num_training_batches*epoch+minibatch_index
            if iteration % 1000 == 0:
                print("Training mini-batch number {0}".format(iteration))
            cost_ij = train_mb(minibatch_index)
            if (iteration+1) % num_training_batches == 0:
                validation_accuracy = np.mean(
                    [validate_mb_accuracy(j) for j in xrange(num_validation_batches)])
                print("Epoch {0}: validation accuracy {1:.2%}".format(
                    epoch, validation_accuracy))
                if validation_accuracy >= best_validation_accuracy:
                    print("This is the best validation accuracy to date.")
                    best_validation_accuracy = validation_accuracy
                    best_iteration = iteration
                    if test_data:
                        test_accuracy = np.mean(
                            [test_mb_accuracy(j) for j in xrange(num_test_batches)])
                        print('The corresponding test accuracy is {0:.2%}'.format(
                            test_accuracy))
    print("Finished training network.")
    print("Best validation accuracy of {0:.2%} obtained at iteration {1}".format(
        best_validation_accuracy, best_iteration))
    print("Corresponding test accuracy of {0:.2%}".format(test_accuracy))

正则化和梯度求解　

首先求每个迭代期需要计算多少次mini-batch。接着定义正则化代价函数，这里使用的是L2正则化。紧接着定义符号化求梯度方法以及梯度更新方法。具体代码含义如下：

1
2
grads = T.grad(cost, self.params)#第一个参数是要求梯度的式子，第二个参数是要对什么参数求梯度
updates = [(param, param-eta*grad) for param, grad in zip(self.params, grads)]#更新

　　注意上述都是符号化定义，并未实际运行。

训练方法定义　　

　　紧接着定义训练方法，使用theano.function方法。第一个参数是输入，即mini-batch的编号，使用的是long类型，即T.lscalar。第二个参数是返回值，即代价值。其他参数updates定义参数的更新，givens用于提供mini-batch训练数据及分类。
　　对于验证方法和测试方法，第一个参数仍然是输入编号，第二个参数是返回值，即正确率，updates参数用于提供mini-batch数据及分类。
　　上述都是属于符号化定义。下面开始实际的训练。

实际训练

　　最外层循环是epoch轮次，再里面一层是每个轮次需要运行的Mini_batch数目。首先，计算目前为止的迭代数，一个mini_batch的计算代表一次迭代。每1000次迭代就输出提示，按照一次训练mini-batch-size=10条数据，1000次迭代就有10000条数据经过了训练。每次训练cost_ij = train_mb(minibatch_index)，都会先进行前向传播计算输出，然后计算代价，进而计算梯度并更新参数。(iteration+1) % num_training_batches == 0代表一次轮次epoch结束。此时对验证集进行验证，验证过程中，会对验证集数据进行前向传播计算输出，具体计算符号定义是在set_inpt中定义的。如果此时验证集准确率比之前轮次的高，则使用得到的模型计算测试集准确率，测试集准确率计算同验证集。
　　最后输出最好的结果以及迭代次数。

结果分析

迭代过程

　　尝试对比不采取弃权策略和采取弃权策略的结果。
　　下面是不采取弃权策略,即p_dropout=0的结果，截取了20个轮次。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
Training mini-batch number 0
Training mini-batch number 1000
Training mini-batch number 2000
Training mini-batch number 3000
Training mini-batch number 4000
Epoch 0: validation accuracy 93.92%
This is the best validation accuracy to date.
The corresponding test accuracy is 93.25%
Training mini-batch number 5000
Training mini-batch number 6000
Training mini-batch number 7000
Training mini-batch number 8000
Training mini-batch number 9000
Epoch 1: validation accuracy 96.26%
This is the best validation accuracy to date.
The corresponding test accuracy is 96.03%
Training mini-batch number 10000
Training mini-batch number 11000
Training mini-batch number 12000
Training mini-batch number 13000
Training mini-batch number 14000
Epoch 2: validation accuracy 97.14%
This is the best validation accuracy to date.
The corresponding test accuracy is 96.93%
Training mini-batch number 15000
Training mini-batch number 16000
Training mini-batch number 17000
Training mini-batch number 18000
Training mini-batch number 19000
Epoch 3: validation accuracy 97.62%
This is the best validation accuracy to date.
The corresponding test accuracy is 97.40%
Training mini-batch number 20000
Training mini-batch number 21000
Training mini-batch number 22000
Training mini-batch number 23000
Training mini-batch number 24000
Epoch 4: validation accuracy 97.88%
This is the best validation accuracy to date.
The corresponding test accuracy is 97.73%
Training mini-batch number 25000
Training mini-batch number 26000
Training mini-batch number 27000
Training mini-batch number 28000
Training mini-batch number 29000
Epoch 5: validation accuracy 98.08%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.00%
Training mini-batch number 30000
Training mini-batch number 31000
Training mini-batch number 32000
Training mini-batch number 33000
Training mini-batch number 34000
Epoch 6: validation accuracy 98.19%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.18%
Training mini-batch number 35000
Training mini-batch number 36000
Training mini-batch number 37000
Training mini-batch number 38000
Training mini-batch number 39000
Epoch 7: validation accuracy 98.28%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.25%
Training mini-batch number 40000
Training mini-batch number 41000
Training mini-batch number 42000
Training mini-batch number 43000
Training mini-batch number 44000
Epoch 8: validation accuracy 98.32%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.34%
Training mini-batch number 45000
Training mini-batch number 46000
Training mini-batch number 47000
Training mini-batch number 48000
Training mini-batch number 49000
Epoch 9: validation accuracy 98.34%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.41%
Training mini-batch number 50000
Training mini-batch number 51000
Training mini-batch number 52000
Training mini-batch number 53000
Training mini-batch number 54000
Epoch 10: validation accuracy 98.42%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.45%
Training mini-batch number 55000
Training mini-batch number 56000
Training mini-batch number 57000
Training mini-batch number 58000
Training mini-batch number 59000
Epoch 11: validation accuracy 98.44%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.45%
Training mini-batch number 60000
Training mini-batch number 61000
Training mini-batch number 62000
Training mini-batch number 63000
Training mini-batch number 64000
Epoch 12: validation accuracy 98.40%
Training mini-batch number 65000
Training mini-batch number 66000
Training mini-batch number 67000
Training mini-batch number 68000
Training mini-batch number 69000
Epoch 13: validation accuracy 98.44%
Training mini-batch number 70000
Training mini-batch number 71000
Training mini-batch number 72000
Training mini-batch number 73000
Training mini-batch number 74000
Epoch 14: validation accuracy 98.44%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.40%
Training mini-batch number 75000
Training mini-batch number 76000
Training mini-batch number 77000
Training mini-batch number 78000
Training mini-batch number 79000
Epoch 15: validation accuracy 98.46%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.42%
Training mini-batch number 80000
Training mini-batch number 81000
Training mini-batch number 82000
Training mini-batch number 83000
Training mini-batch number 84000
Epoch 16: validation accuracy 98.48%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.42%
Training mini-batch number 85000
Training mini-batch number 86000
Training mini-batch number 87000
Training mini-batch number 88000
Training mini-batch number 89000
Epoch 17: validation accuracy 98.48%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.42%
Training mini-batch number 90000
Training mini-batch number 91000
Training mini-batch number 92000
Training mini-batch number 93000
Training mini-batch number 94000
Epoch 18: validation accuracy 98.50%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.42%
Training mini-batch number 95000
Training mini-batch number 96000
Training mini-batch number 97000
Training mini-batch number 98000
Training mini-batch number 99000
Epoch 19: validation accuracy 98.51%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.43%
Training mini-batch number 100000
Training mini-batch number 101000
Training mini-batch number 102000
Training mini-batch number 103000
Training mini-batch number 104000
Epoch 20: validation accuracy 98.57%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.47%

　　下面是采取弃权策略，并设p_dropout=0.3的结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
Training mini-batch number 0
Training mini-batch number 1000
Training mini-batch number 2000
Training mini-batch number 3000
Training mini-batch number 4000
Epoch 0: validation accuracy 93.39%
This is the best validation accuracy to date.
The corresponding test accuracy is 92.51%
Training mini-batch number 5000
Training mini-batch number 6000
Training mini-batch number 7000
Training mini-batch number 8000
Training mini-batch number 9000
Epoch 1: validation accuracy 96.30%
This is the best validation accuracy to date.
The corresponding test accuracy is 95.87%
Training mini-batch number 10000
Training mini-batch number 11000
Training mini-batch number 12000
Training mini-batch number 13000
Training mini-batch number 14000
Epoch 2: validation accuracy 97.35%
This is the best validation accuracy to date.
The corresponding test accuracy is 96.94%
Training mini-batch number 15000
Training mini-batch number 16000
Training mini-batch number 17000
Training mini-batch number 18000
Training mini-batch number 19000
Epoch 3: validation accuracy 97.82%
This is the best validation accuracy to date.
The corresponding test accuracy is 97.45%
Training mini-batch number 20000
Training mini-batch number 21000
Training mini-batch number 22000
Training mini-batch number 23000
Training mini-batch number 24000
Epoch 4: validation accuracy 98.14%
This is the best validation accuracy to date.
The corresponding test accuracy is 97.93%
Training mini-batch number 25000
Training mini-batch number 26000
Training mini-batch number 27000
Training mini-batch number 28000
Training mini-batch number 29000
Epoch 5: validation accuracy 98.13%
Training mini-batch number 30000
Training mini-batch number 31000
Training mini-batch number 32000
Training mini-batch number 33000
Training mini-batch number 34000
Epoch 6: validation accuracy 98.26%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.23%
Training mini-batch number 35000
Training mini-batch number 36000
Training mini-batch number 37000
Training mini-batch number 38000
Training mini-batch number 39000
Epoch 7: validation accuracy 98.56%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.48%
Training mini-batch number 40000
Training mini-batch number 41000
Training mini-batch number 42000
Training mini-batch number 43000
Training mini-batch number 44000
Epoch 8: validation accuracy 98.59%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.53%
Training mini-batch number 45000
Training mini-batch number 46000
Training mini-batch number 47000
Training mini-batch number 48000
Training mini-batch number 49000
Epoch 9: validation accuracy 98.59%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.68%
Training mini-batch number 50000
Training mini-batch number 51000
Training mini-batch number 52000
Training mini-batch number 53000
Training mini-batch number 54000
Epoch 10: validation accuracy 98.72%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.78%
Training mini-batch number 55000
Training mini-batch number 56000
Training mini-batch number 57000
Training mini-batch number 58000
Training mini-batch number 59000
Epoch 11: validation accuracy 98.69%
Training mini-batch number 60000
Training mini-batch number 61000
Training mini-batch number 62000
Training mini-batch number 63000
Training mini-batch number 64000
Epoch 12: validation accuracy 98.74%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.79%
Training mini-batch number 65000
Training mini-batch number 66000
Training mini-batch number 67000
Training mini-batch number 68000
Training mini-batch number 69000
Epoch 13: validation accuracy 98.72%
Training mini-batch number 70000
Training mini-batch number 71000
Training mini-batch number 72000
Training mini-batch number 73000
Training mini-batch number 74000
Epoch 14: validation accuracy 98.77%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.75%
Training mini-batch number 75000
Training mini-batch number 76000
Training mini-batch number 77000
Training mini-batch number 78000
Training mini-batch number 79000
Epoch 15: validation accuracy 98.78%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.82%
Training mini-batch number 80000
Training mini-batch number 81000
Training mini-batch number 82000
Training mini-batch number 83000
Training mini-batch number 84000
Epoch 16: validation accuracy 98.87%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.95%
Training mini-batch number 85000
Training mini-batch number 86000
Training mini-batch number 87000
Training mini-batch number 88000
Training mini-batch number 89000
Epoch 17: validation accuracy 98.83%
Training mini-batch number 90000
Training mini-batch number 91000
Training mini-batch number 92000
Training mini-batch number 93000
Training mini-batch number 94000
Epoch 18: validation accuracy 98.77%
Training mini-batch number 95000
Training mini-batch number 96000
Training mini-batch number 97000
Training mini-batch number 98000
Training mini-batch number 99000
Epoch 19: validation accuracy 98.81%
Training mini-batch number 100000
Training mini-batch number 101000
Training mini-batch number 102000
Training mini-batch number 103000
Training mini-batch number 104000
Epoch 20: validation accuracy 98.79%
Training mini-batch number 105000
Training mini-batch number 106000
Training mini-batch number 107000
Training mini-batch number 108000
Training mini-batch number 109000
Epoch 21: validation accuracy 98.82%
Training mini-batch number 110000
Training mini-batch number 111000
Training mini-batch number 112000
Training mini-batch number 113000
Training mini-batch number 114000
Epoch 22: validation accuracy 98.91%
This is the best validation accuracy to date.
The corresponding test accuracy is 99.00%
Training mini-batch number 115000
Training mini-batch number 116000
Training mini-batch number 117000
Training mini-batch number 118000
Training mini-batch number 119000
Epoch 23: validation accuracy 98.88%
Training mini-batch number 120000
Training mini-batch number 121000
Training mini-batch number 122000
Training mini-batch number 123000
Training mini-batch number 124000
Epoch 24: validation accuracy 98.92%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.93%
Training mini-batch number 125000
Training mini-batch number 126000
Training mini-batch number 127000
Training mini-batch number 128000
Training mini-batch number 129000
Epoch 25: validation accuracy 98.94%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.92%
Training mini-batch number 130000
Training mini-batch number 131000
Training mini-batch number 132000
Training mini-batch number 133000
Training mini-batch number 134000
Epoch 26: validation accuracy 98.87%
Training mini-batch number 135000
Training mini-batch number 136000
Training mini-batch number 137000 
Training mini-batch number 138000
Training mini-batch number 139000
Epoch 27: validation accuracy 98.83%
Training mini-batch number 140000
Training mini-batch number 141000
Training mini-batch number 142000
Training mini-batch number 143000
Training mini-batch number 144000
Epoch 28: validation accuracy 98.88%
Training mini-batch number 145000
Training mini-batch number 146000
Training mini-batch number 147000
Training mini-batch number 148000
Training mini-batch number 149000
Epoch 29: validation accuracy 98.91%
Training mini-batch number 150000
Training mini-batch number 151000
Training mini-batch number 152000
Training mini-batch number 153000
Training mini-batch number 154000
Epoch 30: validation accuracy 98.91%

　　可以发现，刚开始的时候，不采取弃权策略的结果更好。但是随着轮次的增加，采取弃权策略的结果马上就超过了不采取弃权策略的结果，并且采取弃权策略的准确率提升也更快。例如在弃权策略中第16轮次测试集准确率就达到了98.95%，而不采取弃权策略，在更多的第20轮次的测试集结果反而才98.47%。
　　可以看到弃权策略最优结果为第22轮次的99%。
　　实际上可以通过再插入一个卷积层，实现准确率进一步提升到99.22%，如下代码：

1
2
3
4
5
6
7
8
net = Network([
    ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28),
                filter_shape=(20, 1, 5, 5),poolsize=(2, 2)),
    ConvPoolLayer(image_shape=(mini_batch_size, 20, 12, 12),
                filter_shape=(40, 20, 5, 5),poolsize=(2, 2)),
    FullyConnectedLayer(n_in=40*4*4, n_out=100,p_dropout=0.3),
    SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)
net.SGD(training_data, 60, mini_batch_size, 0.1,validation_data, test_data)

　　具体结果:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
Training mini-batch number 0
Training mini-batch number 1000
Training mini-batch number 2000
Training mini-batch number 3000
Training mini-batch number 4000
Epoch 0: validation accuracy 88.52%
This is the best validation accuracy to date.
The corresponding test accuracy is 88.12%
Training mini-batch number 5000
Training mini-batch number 6000
Training mini-batch number 7000
Training mini-batch number 8000
Training mini-batch number 9000
Epoch 1: validation accuracy 96.09%
This is the best validation accuracy to date.
The corresponding test accuracy is 96.08%
Training mini-batch number 10000
Training mini-batch number 11000
Training mini-batch number 12000
Training mini-batch number 13000
Training mini-batch number 14000
Epoch 2: validation accuracy 97.53%
This is the best validation accuracy to date.
The corresponding test accuracy is 97.25%
Training mini-batch number 15000
Training mini-batch number 16000
Training mini-batch number 17000
Training mini-batch number 18000
Training mini-batch number 19000
Epoch 3: validation accuracy 97.80%
This is the best validation accuracy to date.
The corresponding test accuracy is 97.73%
Training mini-batch number 20000
Training mini-batch number 21000
Training mini-batch number 22000
Training mini-batch number 23000
Training mini-batch number 24000
Epoch 4: validation accuracy 98.09%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.11%
Training mini-batch number 25000
Training mini-batch number 26000
Training mini-batch number 27000
Training mini-batch number 28000
Training mini-batch number 29000
Epoch 5: validation accuracy 98.36%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.43%
Training mini-batch number 30000
Training mini-batch number 31000
Training mini-batch number 32000
Training mini-batch number 33000
Training mini-batch number 34000
Epoch 6: validation accuracy 98.38%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.38%
Training mini-batch number 35000
Training mini-batch number 36000
Training mini-batch number 37000
Training mini-batch number 38000
Training mini-batch number 39000
Epoch 7: validation accuracy 98.50%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.63%
Training mini-batch number 40000
Training mini-batch number 41000
Training mini-batch number 42000
Training mini-batch number 43000
Training mini-batch number 44000
Epoch 8: validation accuracy 98.71%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.83%
Training mini-batch number 45000
Training mini-batch number 46000
Training mini-batch number 47000
Training mini-batch number 48000
Training mini-batch number 49000
Epoch 9: validation accuracy 98.75%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.77%
Training mini-batch number 50000
Training mini-batch number 51000
Training mini-batch number 52000
Training mini-batch number 53000
Training mini-batch number 54000
Epoch 10: validation accuracy 98.64%
Training mini-batch number 55000
Training mini-batch number 56000
Training mini-batch number 57000
Training mini-batch number 58000
Training mini-batch number 59000
Epoch 11: validation accuracy 98.79%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.86%
Training mini-batch number 60000
Training mini-batch number 61000
Training mini-batch number 62000
Training mini-batch number 63000
Training mini-batch number 64000
Epoch 12: validation accuracy 98.89%
This is the best validation accuracy to date.
The corresponding test accuracy is 99.00%
Training mini-batch number 65000
Training mini-batch number 66000
Training mini-batch number 67000
Training mini-batch number 68000
Training mini-batch number 69000
Epoch 13: validation accuracy 98.82%
Training mini-batch number 70000
Training mini-batch number 71000
Training mini-batch number 72000
Training mini-batch number 73000
Training mini-batch number 74000
Epoch 14: validation accuracy 98.84%
Training mini-batch number 75000
Training mini-batch number 76000
Training mini-batch number 77000
Training mini-batch number 78000
Training mini-batch number 79000
Epoch 15: validation accuracy 98.86%
Training mini-batch number 80000
Training mini-batch number 81000
Training mini-batch number 82000
Training mini-batch number 83000
Training mini-batch number 84000
Epoch 16: validation accuracy 98.95%
This is the best validation accuracy to date.
The corresponding test accuracy is 99.05%
Training mini-batch number 85000
Training mini-batch number 86000
Training mini-batch number 87000
Training mini-batch number 88000
Training mini-batch number 89000
Epoch 17: validation accuracy 99.01%
This is the best validation accuracy to date.
The corresponding test accuracy is 99.10%
Training mini-batch number 90000
Training mini-batch number 91000
Training mini-batch number 92000
Training mini-batch number 93000
Training mini-batch number 94000
Epoch 18: validation accuracy 98.98%
Training mini-batch number 95000
Training mini-batch number 96000
Training mini-batch number 97000
Training mini-batch number 98000
Training mini-batch number 99000
Epoch 19: validation accuracy 99.02%
This is the best validation accuracy to date.
The corresponding test accuracy is 98.99%
Training mini-batch number 100000
Training mini-batch number 101000
Training mini-batch number 102000
Training mini-batch number 103000
Training mini-batch number 104000
Epoch 20: validation accuracy 99.04%
This is the best validation accuracy to date.
The corresponding test accuracy is 99.08%
Training mini-batch number 105000
Training mini-batch number 106000
Training mini-batch number 107000
Training mini-batch number 108000
Training mini-batch number 109000
Epoch 21: validation accuracy 99.00%
Training mini-batch number 110000
Training mini-batch number 111000
Training mini-batch number 112000
Training mini-batch number 113000
Training mini-batch number 114000
Epoch 22: validation accuracy 99.05%
This is the best validation accuracy to date.
The corresponding test accuracy is 99.07%
Training mini-batch number 115000
Training mini-batch number 116000
Training mini-batch number 117000
Training mini-batch number 118000
Training mini-batch number 119000
Epoch 23: validation accuracy 98.97%
Training mini-batch number 120000
Training mini-batch number 121000
Training mini-batch number 122000
Training mini-batch number 123000
Training mini-batch number 124000
Epoch 24: validation accuracy 99.07%
This is the best validation accuracy to date.
The corresponding test accuracy is 99.02%
Training mini-batch number 125000
Training mini-batch number 126000
Training mini-batch number 127000
Training mini-batch number 128000
Training mini-batch number 129000
Epoch 25: validation accuracy 99.03%
Training mini-batch number 130000
Training mini-batch number 131000
Training mini-batch number 132000
Training mini-batch number 133000
Training mini-batch number 134000
Epoch 26: validation accuracy 98.99%
Training mini-batch number 135000
Training mini-batch number 136000
Training mini-batch number 137000
Training mini-batch number 138000
Training mini-batch number 139000 
Epoch 27: validation accuracy 98.97%
Training mini-batch number 140000
Training mini-batch number 141000
Training mini-batch number 142000
Training mini-batch number 143000
Training mini-batch number 144000
Epoch 28: validation accuracy 99.12%
This is the best validation accuracy to date.
The corresponding test accuracy is 99.22%
Training mini-batch number 145000
Training mini-batch number 146000
Training mini-batch number 147000
Training mini-batch number 148000
Training mini-batch number 149000
Epoch 29: validation accuracy 99.01%
Training mini-batch number 150000
Training mini-batch number 151000
Training mini-batch number 152000
Training mini-batch number 153000
Training mini-batch number 154000
Epoch 30: validation accuracy 99.01%
Training mini-batch number 155000
Training mini-batch number 156000
Training mini-batch number 157000
Training mini-batch number 158000
Training mini-batch number 159000
Epoch 31: validation accuracy 99.09%
Training mini-batch number 160000
Training mini-batch number 161000
Training mini-batch number 162000
Training mini-batch number 163000
Training mini-batch number 164000
Epoch 32: validation accuracy 99.08%
Training mini-batch number 165000
Training mini-batch number 166000
Training mini-batch number 167000
Training mini-batch number 168000
Training mini-batch number 169000
Epoch 33: validation accuracy 99.04%
Training mini-batch number 170000
Training mini-batch number 171000
Training mini-batch number 172000
Training mini-batch number 173000
Training mini-batch number 174000
Epoch 34: validation accuracy 99.06%
Training mini-batch number 175000
Training mini-batch number 176000
Training mini-batch number 177000
Training mini-batch number 178000
Training mini-batch number 179000
Epoch 35: validation accuracy 99.08%
Training mini-batch number 180000
Training mini-batch number 181000
Training mini-batch number 182000
Training mini-batch number 183000
Training mini-batch number 184000
Epoch 36: validation accuracy 99.09%
Training mini-batch number 185000
Training mini-batch number 186000
Training mini-batch number 187000
Training mini-batch number 188000
Training mini-batch number 189000
Epoch 37: validation accuracy 99.07%
Training mini-batch number 190000

　　可以看到，第28 Epoch的时候，测试集准确率达到最高的99.22%。
　　后面，我闲暇之余又进行了更多次的迭代，测试集准确率最终在68 epoch时达到了99.30%。

可视化

　　本部分将挑选出10000条测试集数据中被误分类的数字进行可视化，选择的分类模型是使用弃权策略并且包含一个卷积层、一个全连接层、一个柔性最大值输出层的神经网络结构，测试集准确率达到90%。因此10000条测试集中有100条数据被误分类。可视化代码如下，该部分代码根据示例代码进行改造得到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
def get_error_locations(net, test_data):
    test_x, test_y = test_data

    i = T.lscalar()  # mini-batch index
    net.test_mb_predictions = theano.function(
        [i], net.layers[-1].y_out,
        givens={
            net.x:
                test_x[i * net.mini_batch_size: (i + 1) * net.mini_batch_size]
        })
    test_predictions = list(np.concatenate(
        [net.test_mb_predictions(i) for i in xrange(size(test_data)/net.mini_batch_size)]))

    test_y_eval = test_y.eval()

    error_locations = [j for j in xrange(len(test_y_eval))
                       if test_predictions[j] != test_y_eval[j]]

    erroneous_predictions = [test_predictions[j]
                             for j in error_locations]
    return error_locations, erroneous_predictions

def plot_errors(error_locations, erroneous_predictions=None, test_data=None):
    test_x, test_y = test_data[0].eval(), test_data[1].eval()
    fig = plt.figure()
    error_images = [np.array(test_x[i]).reshape(28, -1) for i in error_locations]
    row,col = 12,10
    n = min(row*col, len(error_locations))
    for j in range(n):
        ax = plt.subplot2grid((row, col), (j/col, j % col))
        ax.matshow(error_images[j], cmap = matplotlib.cm.binary)
        ax.text(24, 5, test_y[error_locations[j]])
        if erroneous_predictions:
            ax.text(24, 24, erroneous_predictions[j])
        plt.xticks(np.array([]))
        plt.yticks(np.array([]))
    plt.tight_layout()
    plt.show()

# draw
error_locations, erroneous_predictions = get_error_locations(net, test_data)
plot_errors(error_locations, erroneous_predictions,test_data)

　　得到下图：
cnn_error_digits
　　如图是误分类的数字，每个数字的右上角是真实的分类，右下角是模型预测的分类。我们可以观察下这100个数字，有些数字即使是我们自己去分类，也很难分辨出来，确实很模棱两可，甚至有些分类我们更认同模型的结果。比如，第一行第8个数，我更认为是9而不是4;第一行第9个数，长得更像9而不是8。因此模型的输出很大程度上是可以接受的。
　　更进一步，我使用上述两层卷积结构的神经网络达到的99.30%测试集准确率模型，进行了一次绘图，得到下图，只有70个误分类的数字：
cnn_error_digits_double_conv
　　我们可以对比一下上面两幅图，看看哪些之前误分类的数字，双层卷积神经网络进行了正确的识别。

保存和加载模型

　　根据训练过程，我们可以知道上述过程是非常缓慢的。为了测试方便，我们不希望每次都要重新进行训练。因此需要找一个保存和加载模型的方法，这也是书上课后的一个小作业。具体代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import cPickle
def save(layers, filename="../model/params.pkl"):
    save_file = open(filename, 'wb')  # this will overwrite current contents
    for layer in layers:
        cPickle.dump(layer.w.get_value(borrow=True), save_file, -1)
        cPickle.dump(layer.b.get_value(borrow=True), save_file, -1)
    save_file.close()

def load(layers, filename="../model/params.pkl"):
    save_file = open(filename,'rb')
    for layer in layers:
        w_param = cPickle.load(save_file)
        b_param = cPickle.load(save_file)
        layer.w.set_value(w_param, borrow=True)
        layer.b.set_value(b_param, borrow=True)
    save_file.close()


#load(net.layers)#加载模型
#save(net.layers)#保存模型

　　这里有个保存模型小小的技巧。如果不想在所有迭代都跑完才进行模型保存的话，可以使用该技巧在任意迭代期手动进行模型的保存。这里针对的是使用pycharm进行python代码coding的同学，可以直接debug整个程序，开始时忽略断点直接运行，然后在你感觉某个epoch后，模型的结果不错的时候，想保存下模型，那么可以打开断点，使程序暂时停止执行，然后使用evaluate expression(alt+F8)功能，直接调用save(net.layers,”../model/param-epoch-轮次数-准确率.pkl”)进行模型的保存。当然，也可以直接写代码，让结果超过你的预期性能的时候，自动进行保存也是可以的。
　　这样，只需要简单的修改下SGD方法，当模型是从文件中加载进来的时候，就不需要进行迭代训练，直接进行结果的预测即可。修改过的完整代码如下。

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
"""network3.py
~~~~~~~~~~~~~~

A Theano-based program for training and running simple neural
networks.

Supports several layer types (fully connected, convolutional, max
pooling, softmax), and activation functions (sigmoid, tanh, and
rectified linear units, with more easily added).

When run on a CPU, this program is much faster than network.py and
network2.py.  However, unlike network.py and network2.py it can also
be run on a GPU, which makes it faster still.

Because the code is based on Theano, the code is different in many
ways from network.py and network2.py.  However, where possible I have
tried to maintain consistency with the earlier programs.  In
particular, the API is similar to network2.py.  Note that I have
focused on making the code simple, easily readable, and easily
modifiable.  It is not optimized, and omits many desirable features.

This program incorporates ideas from the Theano documentation on
convolutional neural nets (notably,
http://deeplearning.net/tutorial/lenet.html ), from Misha Denil's
implementation of dropout (https://github.com/mdenil/dropout ), and
from Chris Olah (http://colah.github.io ).

Written for Theano 0.6 and 0.7, needs some changes for more recent
versions of Theano.

"""

#### Libraries
# Standard library
import cPickle
import gzip

# Third-party libraries
import numpy as np
import theano
import theano.tensor as T
from theano.tensor.nnet import conv
from theano.tensor.nnet import softmax
from theano.tensor import shared_randomstreams
from theano.tensor.signal import pool

# Activation functions for neurons
def linear(z): return z
def ReLU(z): return T.maximum(0.0, z)
from theano.tensor.nnet import sigmoid
from theano.tensor import tanh
import matplotlib
import matplotlib.pyplot as plt
#import seaborn as sns
import cPickle


#### Constants
GPU = False
if GPU:
    print "Trying to run under a GPU.  If this is not desired, then modify "+\
        "network3.py\nto set the GPU flag to False."
    try: theano.config.device = 'gpu'
    except: pass # it's already set
    theano.config.floatX = 'float32'
else:
    print "Running with a CPU.  If this is not desired, then the modify "+\
        "network3.py to set\nthe GPU flag to True."

#### Load the MNIST data
def  load_data_shared(filename="../data/mnist.pkl.gz"):
    f = gzip.open(filename, 'rb')
    training_data, validation_data, test_data = cPickle.load(f)
    print "test len:",len(test_data[0])
    f.close()
    def shared(data):
        """Place the data into shared variables.  This allows Theano to copy
        the data to the GPU, if one is available.

        """
        shared_x = theano.shared(
            np.asarray(data[0], dtype=theano.config.floatX), borrow=True)
        shared_y = theano.shared(
            np.asarray(data[1], dtype=theano.config.floatX), borrow=True)
        return shared_x, T.cast(shared_y, "int32")
    return [shared(training_data), shared(validation_data), shared(test_data)]

#### Main class used to construct and train networks
class Network(object):

    def __init__(self, layers, mini_batch_size):
        """Takes a list of `layers`, describing the network architecture, and
        a value for the `mini_batch_size` to be used during training
        by stochastic gradient descent.

        """
        self.layers = layers
        self.mini_batch_size = mini_batch_size
        self.params = [param for layer in self.layers for param in layer.params]
        self.x = T.matrix("x")
        self.y = T.ivector("y")
        init_layer = self.layers[0]
        init_layer.set_inpt(self.x, self.x, self.mini_batch_size)
        for j in xrange(1, len(self.layers)):
            prev_layer, layer  = self.layers[j-1], self.layers[j]
            layer. set_inpt(
                prev_layer.output, prev_layer.output_dropout, self.mini_batch_size)
        self.output = self.layers[-1].output
        self.output_dropout = self.layers[-1].output_dropout

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            validation_data, test_data, lmbda=0.0, is_load_model_from_file=False):
        """Train the network using mini-batch stochastic gradient descent."""
        training_x, training_y = training_data
        validation_x, validation_y = validation_data
        test_x, test_y = test_data

        # compute number of minibatches for training, validation and testing
        num_training_batches = size(training_data)/mini_batch_size
        num_validation_batches = size(validation_data)/mini_batch_size
        num_test_batches = size(test_data)/mini_batch_size

        # define the (regularized) cost function, symbolic gradients, and updates
        l2_norm_squared = sum([(layer.w**2).sum() for layer in self.layers])
        cost = self.layers[-1].cost(self)+\
               0.5*lmbda*l2_norm_squared/num_training_batches
        grads = T.grad(cost, self.params)
        updates = [(param, param-eta*grad)
                   for param, grad in zip(self.params, grads)]

        # define functions to train a mini-batch, and to compute the
        # accuracy in validation and test mini-batches.
        i = T.lscalar() # mini-batch index
        train_mb = theano.function(
            [i], cost, updates=updates,
            givens={
                self.x:
                training_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
                self.y:
                training_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
            })
        validate_mb_accuracy = theano.function(
            [i], self.layers[-1].accuracy(self.y),
            givens={
                self.x:
                validation_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
                self.y:
                validation_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
            })
        test_mb_accuracy = theano.function(
            [i], self.layers[-1].accuracy(self.y),
            givens={
                self.x:
                test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size],
                self.y:
                test_y[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
            })
        self.test_mb_predictions = theano.function(
            [i], self.layers[-1].y_out,
            givens={
                self.x:
                test_x[i*self.mini_batch_size: (i+1)*self.mini_batch_size]
            })

        # Load model from file
        if is_load_model_from_file:
            print 'use the model loaded from file...'
            test_accuracy = np.mean(
                [test_mb_accuracy(j) for j in xrange(num_test_batches)])
            print('The corresponding test accuracy is {0:.2%}'.format(
                test_accuracy))

        # Do the actual training
        else:
            print "begin training..."
            best_validation_accuracy = 0.0
            for epoch in xrange(epochs):
                for minibatch_index in xrange(num_training_batches):
                    iteration = num_training_batches * epoch + minibatch_index
                    if iteration % 1000 == 0:
                        print("Training mini-batch number {0}".format(iteration))
                    cost_ij = train_mb(minibatch_index)
                    if (iteration + 1) % num_training_batches == 0:
                        validation_accuracy = np.mean(
                            [validate_mb_accuracy(j) for j in xrange(num_validation_batches)])
                        print("Epoch {0}: validation accuracy {1:.2%}".format(
                            epoch, validation_accuracy))
                        if validation_accuracy >= best_validation_accuracy:
                            print("This is the best validation accuracy to date.")
                            best_validation_accuracy = validation_accuracy
                            best_iteration = iteration
                            if test_data:
                                test_accuracy = np.mean(
                                    [test_mb_accuracy(j) for j in xrange(num_test_batches)])
                                print('The corresponding test accuracy is {0:.2%}'.format(
                                    test_accuracy))
            print("Finished training network.")
            print("Best validation accuracy of {0:.2%} obtained at iteration {1}".format(
                best_validation_accuracy, best_iteration))
            print("Corresponding test accuracy of {0:.2%}".format(test_accuracy))


#### Define layer types

class ConvPoolLayer(object):
    """Used to create a combination of a convolutional and a max-pooling
    layer.  A more sophisticated implementation would separate the
    two, but for our purposes we'll always use them together, and it
    simplifies the code, so it makes sense to combine them.

    """

    def __init__(self, filter_shape, image_shape, poolsize=(2, 2),
                 activation_fn=sigmoid):
        """`filter_shape` is a tuple of length 4, whose entries are the number
        of filters, the number of input feature maps, the filter height, and the
        filter width.

        `image_shape` is a tuple of length 4, whose entries are the
        mini-batch size, the number of input feature maps, the image
        height, and the image width.

        `poolsize` is a tuple of length 2, whose entries are the y and
        x pooling sizes.

        """
        self.filter_shape = filter_shape
        self.image_shape = image_shape
        self.poolsize = poolsize
        self.activation_fn=activation_fn
        # initialize weights and biases
        n_out = (filter_shape[0]*np.prod(filter_shape[2:])/np.prod(poolsize))
        self.w = theano.shared(
            np.asarray(
                np.random.normal(loc=0, scale=np.sqrt(1.0/n_out), size=filter_shape),
                dtype=theano.config.floatX),
            borrow=True)
        self.b = theano.shared(
            np.asarray(
                np.random.normal(loc=0, scale=1.0, size=(filter_shape[0],)),
                dtype=theano.config.floatX),
            borrow=True)
        self.params = [self.w, self.b]

    def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
        self.inpt = inpt.reshape(self.image_shape)
        conv_out = conv.conv2d(
            input=self.inpt, filters=self.w, filter_shape=self.filter_shape,
            image_shape=self.image_shape)
        pooled_out = pool.pool_2d(
            input=conv_out, ds=self.poolsize, ignore_border=True, mode='max')
        self.output = self.activation_fn(
            pooled_out + self.b.dimshuffle('x', 0, 'x', 'x'))
        self.output_dropout = self.output # no dropout in the convolutional layers

class FullyConnectedLayer(object):

    def __init__(self, n_in, n_out, activation_fn=sigmoid, p_dropout=0.0):
        self.n_in = n_in
        self.n_out = n_out
        self.activation_fn = activation_fn
        self.p_dropout = p_dropout
        # Initialize weights and biases
        self.w = theano.shared(
            np.asarray(
                np.random.normal(
                    loc=0.0, scale=np.sqrt(1.0/n_out), size=(n_in, n_out)),
                dtype=theano.config.floatX),
            name='w', borrow=True)
        self.b = theano.shared(
            np.asarray(np.random.normal(loc=0.0, scale=1.0, size=(n_out,)),
                       dtype=theano.config.floatX),
            name='b', borrow=True)
        self.params = [self.w, self.b]

    def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
        self.inpt = inpt.reshape((mini_batch_size, self.n_in))
        self.output = self.activation_fn(
            (1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
        self.y_out = T.argmax(self.output, axis=1)
        self.inpt_dropout = dropout_layer(
            inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
        self.output_dropout = self.activation_fn(
            T.dot(self.inpt_dropout, self.w) + self.b)

    def accuracy(self, y):
        "Return the accuracy for the mini-batch."
        return T.mean(T.eq(y, self.y_out))


class SoftmaxLayer(object):

    def __init__(self, n_in, n_out, p_dropout=0.0):
        self.n_in = n_in
        self.n_out = n_out
        self.p_dropout = p_dropout
        # Initialize weights and biases
        self.w = theano.shared(
            np.zeros((n_in, n_out), dtype=theano.config.floatX),
            name='w', borrow=True)
        self.b = theano.shared(
            np.zeros((n_out,), dtype=theano.config.floatX),
            name='b', borrow=True)
        self.params = [self.w, self.b]

    def set_inpt(self, inpt, inpt_dropout, mini_batch_size):
        self.inpt = inpt.reshape((mini_batch_size, self.n_in))
        self.output = softmax((1-self.p_dropout)*T.dot(self.inpt, self.w) + self.b)
        self.y_out = T.argmax(self.output, axis=1)
        self.inpt_dropout = dropout_layer(
            inpt_dropout.reshape((mini_batch_size, self.n_in)), self.p_dropout)
        self.output_dropout = softmax(T.dot(self.inpt_dropout, self.w) + self.b)

    def cost(self, net):
        "Return the log-likelihood cost."
        return -T.mean(T.log(self.output_dropout)[T.arange(net.y.shape[0]), net.y])

    def accuracy(self, y):
        "Return the accuracy for the mini-batch."
        return T.mean(T.eq(y, self.y_out))


#### Miscellanea
def size(data):
    "Return the size of the dataset `data`."
    return data[0].get_value(borrow=True).shape[0]

def dropout_layer(layer, p_dropout):
    srng = shared_randomstreams.RandomStreams(
        np.random.RandomState(0).randint(999999))
    mask = srng.binomial(n=1, p=1-p_dropout, size=layer.shape)
    return layer*T.cast(mask, theano.config.floatX)


def get_error_locations(net, test_data):
    test_x, test_y = test_data

    i = T.lscalar()  # mini-batch index
    net.test_mb_predictions = theano.function(
        [i], net.layers[-1].y_out,
        givens={
            net.x:
                test_x[i * net.mini_batch_size: (i + 1) * net.mini_batch_size]
        })
    test_predictions = list(np.concatenate(
        [net.test_mb_predictions(i) for i in xrange(size(test_data)/net.mini_batch_size)]))

    test_y_eval = test_y.eval()

    error_locations = [j for j in xrange(len(test_y_eval))
                       if test_predictions[j] != test_y_eval[j]]

    erroneous_predictions = [test_predictions[j]
                             for j in error_locations]

    return error_locations, erroneous_predictions


def plot_errors(error_locations, erroneous_predictions=None, test_data=None):
    test_x, test_y = test_data[0].eval(), test_data[1].eval()
    fig = plt.figure()
    error_images = [np.array(test_x[i]).reshape(28, -1) for i in error_locations]
    row,col = 12,10
    n = min(row*col, len(error_locations))
    for j in range(n):
        ax = plt.subplot2grid((row, col), (j/col, j % col))
        ax.matshow(error_images[j], cmap = matplotlib.cm.binary)
        ax.text(24, 5, test_y[error_locations[j]])
        if erroneous_predictions:
            ax.text(24, 24, erroneous_predictions[j])
        plt.xticks(np.array([]))
        plt.yticks(np.array([]))
    plt.tight_layout()
    plt.show()



def save(layers, filename="../model/params.pkl"):
    save_file = open(filename, 'wb')  # this will overwrite current contents
    for layer in layers:
        cPickle.dump(layer.w.get_value(borrow=True), save_file, -1)
        cPickle.dump(layer.b.get_value(borrow=True), save_file, -1)
    save_file.close()

def load(layers, filename="../model/params.pkl"):
    save_file = open(filename,'rb')
    for layer in layers:
        w_param = cPickle.load(save_file)
        b_param = cPickle.load(save_file)
        layer.w.set_value(w_param, borrow=True)
        layer.b.set_value(b_param, borrow=True)
    save_file.close()


# running
if __name__ == "__main__":
    is_load_model_from_file = False

    training_data, validation_data, test_data = load_data_shared()
    mini_batch_size = 10
    net = Network(
         [ConvPoolLayer(image_shape=(mini_batch_size, 1, 28, 28), filter_shape=(20, 1, 5, 5), poolsize=(2, 2)),
            FullyConnectedLayer(n_in=20 * 12 * 12, n_out=100, p_dropout=0.3),
            SoftmaxLayer(n_in=100, n_out=10)], mini_batch_size)

    if is_load_model_from_file:
        load(net.layers)

    net.SGD(training_data, 30, mini_batch_size, 0.1, validation_data, test_data, is_load_model_from_file=is_load_model_from_file)

    # if training,then save model
    if is_load_model_from_file == False:
        save(net.layers)

    # draw error classification digits
    error_locations, erroneous_predictions=get_error_locations(net, test_data)
    plot_errors(error_locations, erroneous_predictions,test_data)

参考

神经网络和深度学习入门
Theano教程

坚持原创技术分享，您的支持将鼓励我继续创作！