　　本文是针对卜东波老师算法设计与分析第一课做的课堂笔记。第一课主要介绍算法的概念以及一些代表性的问题。

算法起源

　　算法(Algorithm)一词的起源来自Muhammad ibn Musa al-Khwarizmi(C. 780-650),如下图：

　　算法的艺术可以类比成米开朗琪罗雕刻的艺术：

　　上述是指，理解算法必须看清算法问题本身的结构。

解算法问题的基本方法

算法问题的产生过程

　　【Practical Problems】—-Topic Choosing—-> 【A Practical Problem】—-Formulation—–>【Math/Algorithm Problem】—-Key Observation—->【Solution】
　　任何算法产生的步骤大致如上。不同学科的研究人员关注的点也不一样，例如研究数学的可能认为Formulation最重要；研究计算机的可能认为Key Observation最重要；但实际上Topic Choosing才是最重要的，因为Topic Choosing反映了这个实际算法问题的本质。作为计算机专业的，我们重点来研究Key Observation，通过观察来发现算法的本质，可通过观察算法的结构(Structure)以及解的形式(Solution Forms)来发现。

算法求解方法

　　首先进行算法结构的观察。如上图所示，对于一个实际的问题，首先进行形式化。我们所研究的问题大致可以分成可进行组合优化求解的问题或者通过统计(statistic)学习方法求解的问题。组合优化(Combinatorial Optimization),是指寻找离散事件的最优编排、分组、次序或筛选，是运筹学的一个分支。参考组合最优化。而统计学习则是机器学习领域主要的方法。
　　算法设计与分析课主要研究一类可进行组合优化的问题。组合优化问题当中，有一类可进行自我分解(SELF-REDUCTION)从而降低问题规模的问题，这类问题通常可以通过数学归纳法(INDUCTION)来证明求解的可行性，包括DC(Divide And Conquer)分治算法、DP(Dynamic Programming)动态规划问题，最优子结构是DP的前提。另一类问题是不能够通过分解来降低问题规模，此时可以使用反复迭代来逐步提升(IMPROVEMENT)性能，通常从一个初始解开始，然后一步一步提升性能，这类问题包括LP/SDP/NF/LS/MC/SA等。
　　其次进行解形式的观察。对于解形式的观察，我们可以通过SMART ENUMERATION即有策略性的枚举来发现规律或求解问题的方法。例如最优化问题(optimal)可以化成近似(approximation)问题，通过枚举近似解来观察；对于确定性问题(deterministic)可以通过枚举化成随机化(randomization)问题;特殊(special cases)情况通过枚举实际(Practical)情况来观察。这类观察解形式来发现求解问题的方法的典型代表包括Greedy贪心算法等。
　　总之，要时刻关注问题的求解策略，选择最合适的方法，INDUCTION、IMPROVEMENT、ENUMERATION，所有算法问题的求解不外乎这3种方法。

案例分析

　　结合上面三种方法来进行案例分析。

求解最大公约数

　　第一个案例是求解最大公约数。这个问题就是通过分解问题为子问题进行求解。

TSP问题

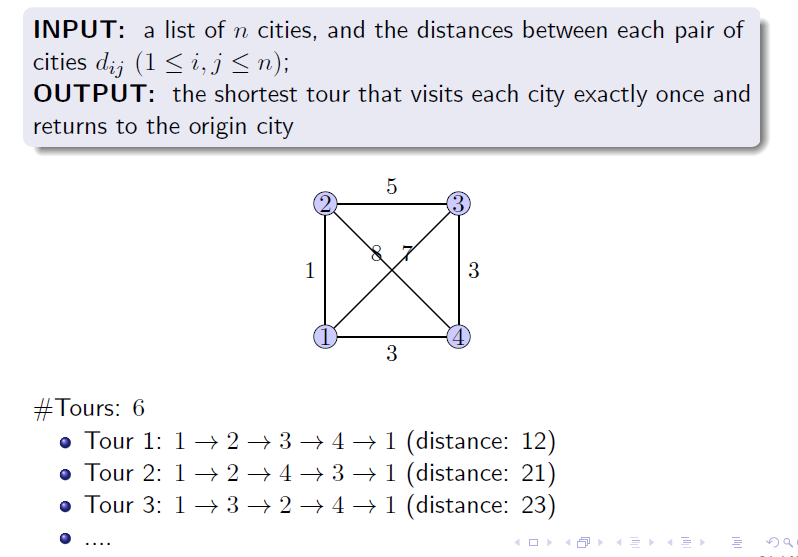
　　上图是旅行商问题的形式化定义。

Method1:Divide And Conquer

　　首先考虑一个相关的问题。考虑最后一步回到起始点的所有可能。如下图，总共有3种情况。

　　再考虑一个更小的问题。

　　如何求解D({2,3,4},4)呢？
　　D({2,3,4},4)意味着要先经过2和3再到达4，因此这里面总共有2种情况。1）起始点1先经过2，再经过3，最后到达4。2）起始点1先经过3，再到达2，最后到达4。因此：
$$D(\{2,3,4\},4)=min{ D(\{2,3\},3)+d_{34}, D(\{2,3\},2)+d_{24}}$$
　　因此算法如下：

Method2:Improvement Strategy

　　首先是解空间的一些基本概念。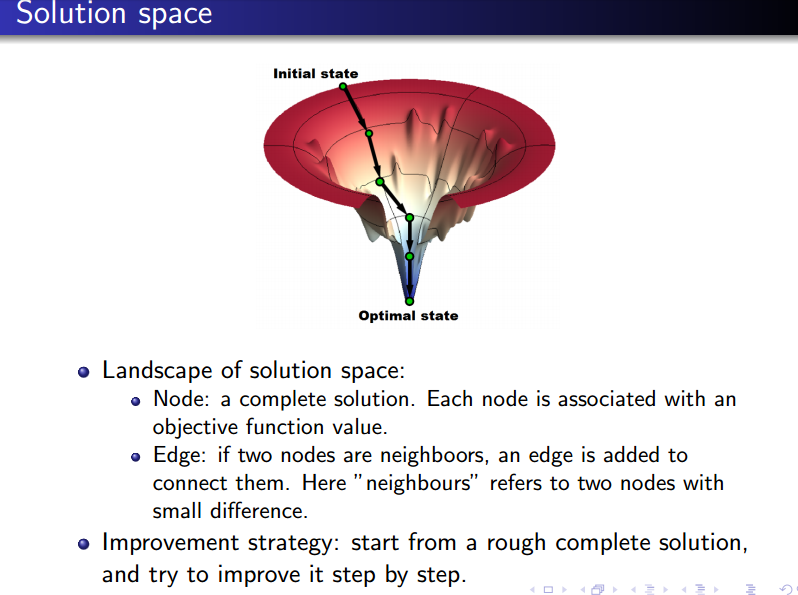

　　其中节点代表的是一个完整的解，边代表的是节点之间存在关联。提升策略意味着会从一个初始解开始，通过略微修改解，来逐步提升性能。

　　提升策略的基本套路如上图所示。
　　这里的关键是如何定义s的领域(neighbourhood)s’。我们的目标是尽量少修改s来变成s’。一种定义方法是如下：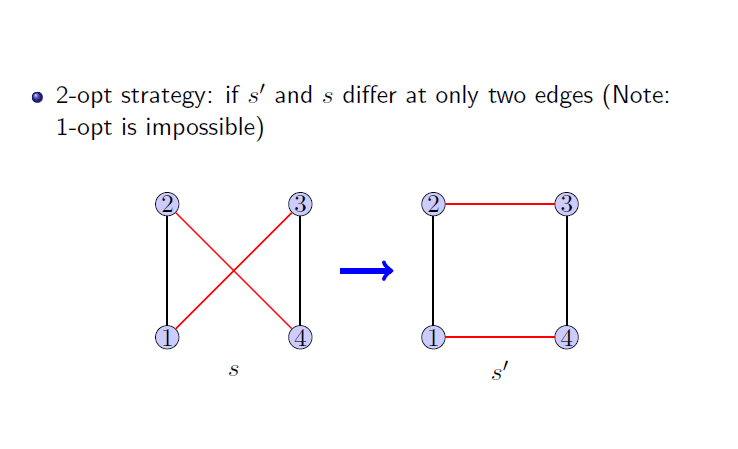

　　下面是一个例子：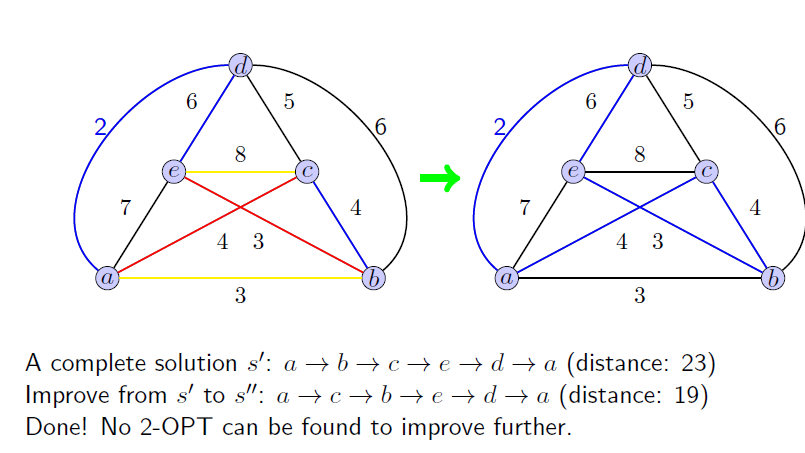

Method3:BackTracking:an intelligent enumeration strategy

　　我们注意到，任意一个解都可以被表示成一个由边构成的序列。

　　回溯树的结构如下：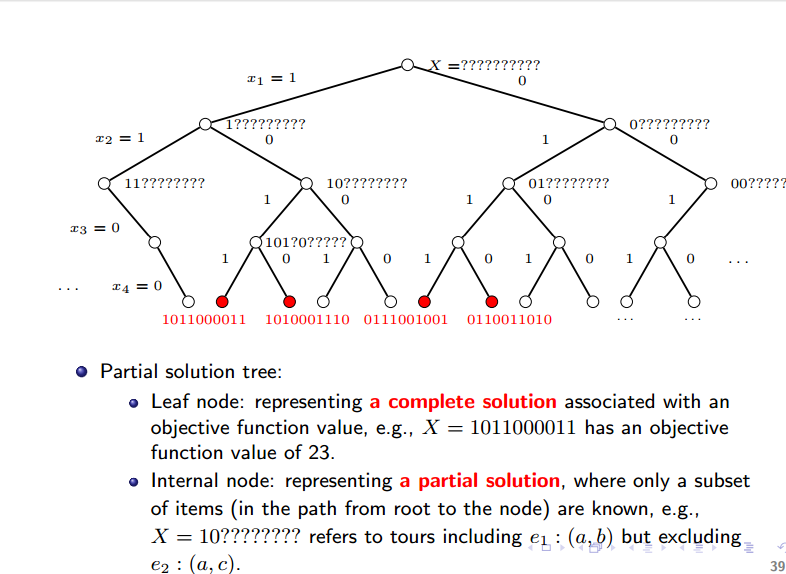

　　注意这里面使用到了预测方法，基于如下两个准则：1）如果去掉连接(i,j)点的边会导致节点i(or j)连接的边少于两条，那么这条边必须包含。(有进必有出)。2）如果增加lianjie(i,j)点的边会导致节点i(or j)连接的边多于两条(只能进一次,出一次)，那么这条边一定不能包含。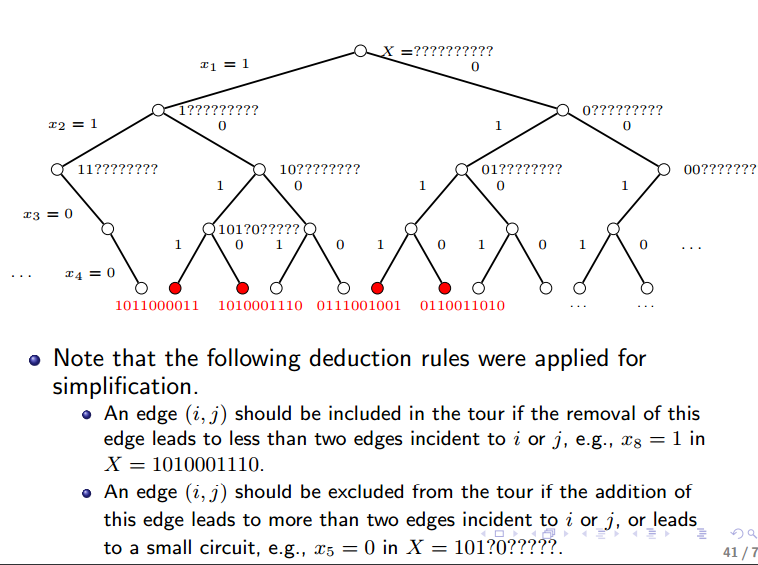

　　算法如下：

　　回溯法的问题是会遍历所有可能的解，这样会导致解空间太大。一种解决方法是使用剪枝策略，对每一个节点，我们计算该节点代价的最小值。如果某个节点代价大于目前最优解，那么该节点及其下面的所有点就不需要进行遍历。

　　对每个节点的下界计算方法如下：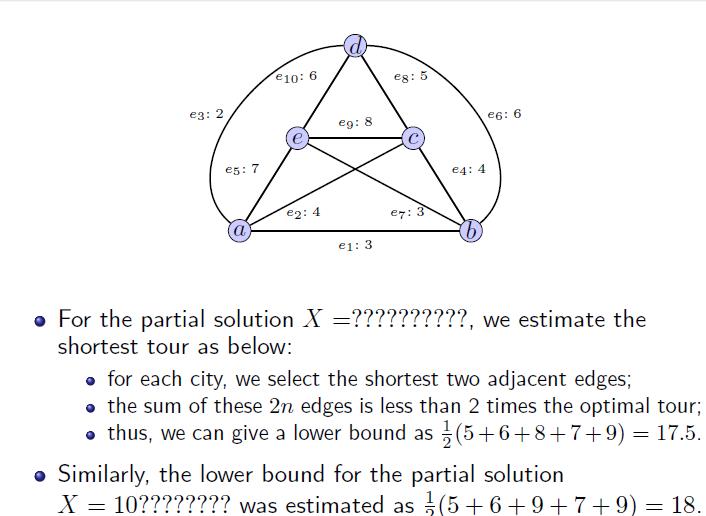

　　修改完的代码如下：

　　１个实例如下：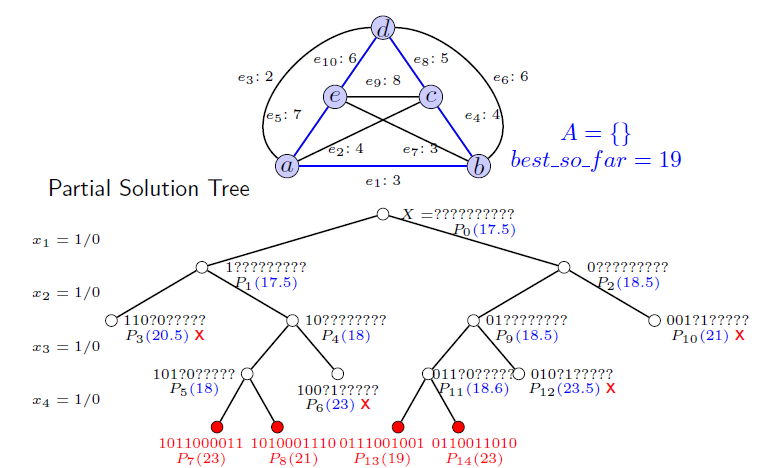

　　对于P2节点，由于e1边没有选，对于a节点而言，下界变成了(2+4)/2;对于b节点而言，因为e1边不能选，下界变成了(3+4)/2。相对于P0节点而言，代价总共增加了1。又比如对于P4节点，由于e2不能选，对于c节点而言，下界变成了(4+5)/2，相对PO总共增加了0.5。