　　本文是Leetcode刷题计划第一周的总结。另外，还包括了一些课堂上学习到的算法的练习，下面将围绕每一道题进行分析。

InPlace Merge

　　第一道题是归并排序。归并排序基本思路是使用分治法进行求解。这里的关键操作在于Merge两个有序的数组。通常的做法是，付出O(n)空间复杂度的代价，新建一个数组，然后使用两个指针分别遍历原数组的左右两边，依次选择较小的值放到新数组，最后复制新数组的值到原数组。(也可以一开始复制原数组左右两边到两个小数组，然后遍历依次放到原数组中)
　　这里面我们付出了O(n)的空间复杂度和O(n)的时间复杂度的代价。能否使得空间复杂度降低为O(1)？

内存反转　　

　　这里使用的是循环移位的策略，也称作内存反转。如下所示：
　　Q:给定序列, $a_1,a_2,…,a_m, b_1,b_2,…,b_n$ ,把它变成 $b_1,b_2,…,b_n, a_1,a_2,…,a_m$ ?
　　A:先对 $a_1,a_2,…,a_m$ 进行反转；再对 $b_1,b_2,…,b_n$ 进行反转，最后再对整体进行反转，就可以得到 $b_1,b_2,…,b_n, a_1,a_2,…,a_m$ 。代码如下：

void exchange(vector<int> &A, int s, int m, int e){
    reverse(A,s, m);
    reverse(A,m+1,e);
    reverse(A, s, e);
}

void swap(vector<int> &A, int x, int y){
    int t = A[x];
    A[x] = A[y];
    A[y] = t;
}
void reverse(vector<int> &A, int s, int e){
    while(s < e){
        swap(A, s++, e--);
    }
}

原地归并

　　假设数据如下图所示：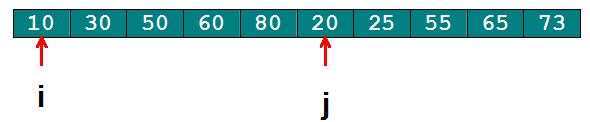

　　开始时 $i,j$ 分别指向这个数组的两个有序子序列的第一个值，然后指针向后移动,直到找到比20大的值，即移动到30，此时我们知道 $i$ 指针之前的值一定是两个子序列最小的块。
　　接着，先用一个临时指针记录 $j$ 的位置。然后把第二个序列的指针 $j$ 向后移动，直到找到比30大的值，即移动到55，即如下图所示：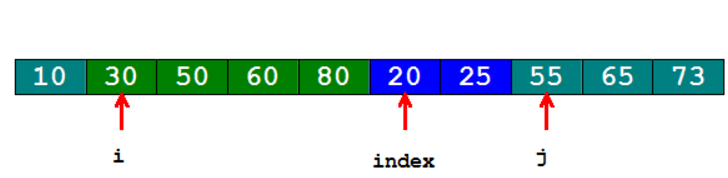

　　这样，我们把[i,index)和[index,j)的内存块进行交换，再移动i指针，移动步长step=j-index，两个子数组的分界点mid也要相应的向后移动step=j-index。如下图：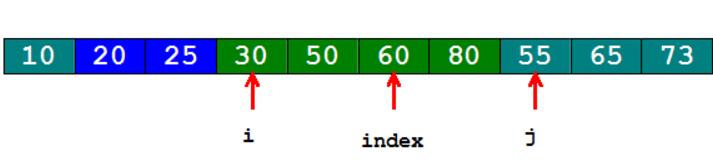

　　这样可以看出 $i$ 之前的都已经排好序，而以 $i$ 开始的子序列和以 $j$ 开始的子序列又是开始的问题模型，同样的操作进行下去最终排序完成。

void inplaceMerge(vector<int> &A, int start, int mid, int end){
    int i = start;
    int j = mid+1;
    while(i <= mid && j <= end){//两个条件都需要测试
        int step = 0;
        while(i <= mid && A[i] <= A[j]){++i;}//找到第一个比A[j]大的数
        
        while(j <= end && A[j] < A[i]){++j;++step;}//找到比A[i]大的所有A[j]
        
        exchange(A, i, mid, j-1);//反转
        i += step; //移动指针
        mid += step;//分割点也要后移
        
    }
}
void sort(vector<int> &A) {
    mergeSort(A, 0,  A.size()-1);
}
    
void mergeSort(vector<int> &A, int start, int end){
    if(start < end){
        int mid = (start + end)/2;
        mergeSort(A, start, mid);
        mergeSort(A, mid+1, end);
        inplaceMerge(A, start, mid, end);
    }
}

Two Sum (#1)

　　问题：给定一个无序数组，在O(n)时间内寻找两个数的和为target，返回这两个数的下标。题目已经保证了结果是唯一的。
　　分析：如果是O(n^2)复杂度，那么只要两个循环遍历就能找到。另外，O(n)时间复杂度意味着不能排序，返回下标也意味着最好不要打乱原数组的顺序。我们联想到哈希表获取元素的时间复杂度为O(1)，如果将数据处理成target-某个数=另一个数，那么使用哈希表查找就能查找到另一个数(key:原始数据,value:下标)。但是由于题目没有保证元素都不相同，因此不能先循环，处理每个数存入哈希表(相同的数会覆盖)。这里使用的是边遍历边存储到哈希表，如果在哈希表中找到另一个数，则直接返回结果，否则将该数存入哈希表中。代码如下：

class Solution {
public:
    /**
    *每个数处理成target-该数 7 2 -2 -6
    *对map进行查找，如果存在等于target-该数的数值，则找到。否则存储map该{原始数据:位置} 题目中说不存在相同的数
    *
    */
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> map;
        vector<int> result;
        for(int i = 0; i < nums.size(); ++i){
            int findNum = target - nums[i];
            if(map.find(findNum) != map.end()){//find查找的是key是否存在
                result.push_back(i);
                result.push_back(map[findNum]);
            }
            map[nums[i]] = i;
        }
        return result;
        
    }
};

　　变型：如果加上一个条件原数组是有序的，那么可以使用另外一种方法找到所有和为target的数据对。
　　分析：可以使用两个指针 $i,j$ ,分别指向有序数组的低端和高端，如果两个指针所在位置的数据之和为target，则加入结果集。如果和小于target，说明 $i$ 指向的数太小了，必须稍微大一点才可以；或者说 $j$ 指向的数不够大，任凭j怎么往左移都没用，因为 $j$ 指向的数最大。因此向右移动 $i$ 指针。如果和大于target，说明 $j$ 指向的太大了，因此往左移动 $j$ 指针。
　　为了去掉重复的结果，需要在和等于target的条件里，移动两个指针，直到遇到不一样的数。

public static List<int[]> twoSum(Integer[] nums, int target) {
    List<int[]> result = new ArrayList<int[]>();
    int i = 0, j = nums.length - 1;
    while(i < j){
        if(nums[i] + nums[j] == target){
            result.add(new int[]{nums[i], nums[j]});
            while(i < j && nums[i+1] == nums[i]){++i;}//filter duplicate
            while(i < j && nums[j-1] == nums[j]){--j;}//filter duplicate
            ++i;
            --j;
        }else if(nums[i] + nums[j] < target){
            ++i;
        }else {
            --j;
        }
    }
    return result;
}

Three Sum (#15)

　　问题：给定一个数组，在O(n^2)复杂度内找出任何3个和为0的数，返回数据对即可。
　　分析：该题可以进行排序求解，返回数据而不是下标。可以利用Two Sum中变型策略。首先固定一个数，然后使用Two Sum求解。即，使用for循环遍历数组，固定当前数，然后找到所有和当前数搭配的和0的其余两个数，即twoTarget = -nums[i]。具体代码如下：

public static List<int[]> threeSum(Integer[] nums) {
    Arrays.sort(nums);
    List<int[]> result = new ArrayList<int[]>();
    for(int i = 0; i < nums.length-1; ++i){
        if(i != 0 && nums[i] == nums[i-1]) //相同元素不需要再查找了
            continue;
        int s = i+1, e = nums.length - 1;
        int target = -nums[i];
        while(s < e){
            int twoSum = nums[s] + nums[e];
            if(twoSum == target) {
                result.add(new int[]{nums[i],nums[s],nums[e]});
                while (s < e && nums[s+1] == nums[s]) ++s;//filter duplicate
                while (s < e && nums[e-1] == nums[e]) --e;//filter duplicate
                ++s;//move
                --e;//move
            }else if(twoSum < target){
                ++s;
            }else{
                --e;
            }
        }
    }
    return result;
}

　　注意上述去重操作。　　

Swap Elements By Xor

　　可以使用异或操作交换数据。原理是使用异或的性质：

任意两个相同的数异或都为0
任意数(1或者0)和0异或都为本身。1 xor 0 = 1, 0 xor 0 = 1;因此式子中有0的地方可以直接去掉0。

异或满足结合律和交换律。

void swap(int &x, int &y){
    if(x == y) return;
    x ^= y; // x = x ^ y
    y ^= x; // y = x ^ y ^ y = x ^ (y ^ y) = x ^ (0) = x 
    x ^= y; // x = x ^ y ^ x =  y
}

　　运行原理如上述代码注释部分。
　　这里有一个陷进，如果两个相同的数传入，实际上交换完没变。但是因为相同的数异或为0，使得x和y都等于0了。因此最好要一开始检查一下是否相同。

Number of 1 Bits(#191)

　　统计位当中1的个数。正常想法就是看看最后1位是不是1，是就累加。然后不断往右移位，直到数变成0为止。如下：

int hammingWeight(uint32_t n){
        int c = 0;
        while(n){
            int t = n & 1;
            if(t){c++;}
            n >>= 1;
        }
        return c;
    }

　　另一种方法，利用 $n \&= (n-1)$ ,该式子会将n最右边的1变成0。如果本身为0,与之后肯定为0不变；如果最右边是1，减一后为0，再&之后就变成0了。

int hammingWeight(uint32_t n) {
    int count = 0;
    while(n){//非零
        ++count;
        n &= (n-1); //关键，每次都会把最靠右边的1变成0。
    }
    return count;
}

Count Bits(#338)

　　问题：统计range(n)范围内所有数当中位为1的个数。要求时间复杂度为O(n)。
　　分析：正常会对每个数求1的个数，复杂度为O(n * sizeof(integer))。这里由于要求出前面数的1的个数，因此可以利用前面的数，动态规划思想。将大的数化成前面小的数。一种方法是，单独抽出最后一位，则原始的数可以往右移1位变成前面的数。

vector<int> countBits(int num) {
        vector<int> result(num+1, 0);
        for(int i = 1; i <= num; ++i){
            result[i] = result[i>>1] + (i & 1);
        }
        return result;
    }

　　另一种，化大数为前面的数，是利用前面提到的将某个数位当中最右边1化为0.则：

1	result[i] = result[i & (i-1)] + 1;

Reverse Bits (#190)

　　问题：反转数的二进制位。
　　分析：可以新建一个数 $m=0$ ,m先左移一位腾出一个位置，然后从原始数的最后一位开始，不断用m求或运算。直到原始数位全部遍历完毕。复杂度为O(sizeof(int)).

uint32_t reverseBits(uint32_t n) {
    uint32_t m = 0;
    for(int i = 0; i < 32; ++i){
        m <<= 1; //先挪出一个位置
        m |= (n & 1);
        n >>= 1;  
    }
    return m;
}

　　另外，还有个O(log sizeof(int))复杂度的算法如下：

uint32_t reverseBits(uint32_t n) {
    n = (n >> 16) | (n << 16);
    n = ((n & 0xff00ff00) >> 8) | ((n & 0x00ff00ff) << 8);
    n = ((n & 0xf0f0f0f0) >> 4) | ((n & 0x0f0f0f0f) << 4);
    n = ((n & 0xcccccccc) >> 2) | ((n & 0x33333333) << 2);
    n = ((n & 0xaaaaaaaa) >> 1) | ((n & 0x55555555) << 1);
    return n;
}

Reverse Integer(#7)

　　问题：反转整数
　　分析：新建一个数result初始化为0，每次取出最后一位，使用result10+最后一位。即可得到逆序。例如：123： ( (0\10+3)* 10)+2)*10 + 1 = 321. 注意溢出的处理，策略是：将求得的结果tmp=result*10+最后一位,根据：(tmp-最后一位）/10，逆序求出result，看看跟原来的result是否相等，不相等说明溢出了。

 int reverse(int x) {
    int result = 0;
    while(x){
        int last = x % 10;
        int tmp = result * 10 + last;
        if((tmp-last)/10 != result) return 0; //溢出
        result = tmp;
        x /= 10; 
    }
    return result;
    //for 8 bit binary number abcdefgh, the process is as follow:
    //abcdefgh -> efghabcd -> ghefcdab -> hgfedcba
}

Judge Route Circle(# 657)

　　问题：机器人上下左右移动，给出一个移动序列，判断是否回到出发点。
　　答：两个数分别统计上下和左右情况，上下抵消，左右抵消。最后都为0则回到原点。

bool judgeCircle(string moves) {
    int x = 0, y = 0;
    for(int i = 0; i < moves.size(); ++i){
        if(moves[i] == 'U'){
            x += 1;
        }else if(moves[i] == 'D'){
            x -= 1;
        }else if(moves[i] == 'R'){
            y += 1;
        }else if(moves[i] == 'L'){
            y -= 1;
        }
    }
    return x == 0 && y == 0;
}

Merge Two Sorted Array(#88)

　　问题：给定两个有序的数组nums1,nums2,要求将nums2 Merge到nums1，使得nums1保持有序。只能利用nums1空间，题目已经保证nums1能保证容纳的下nums2的元素。
　　分析：常规想法是从第一个数开始merge到nums1中，这样就需要移数操作。如下：

void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
        int count_i = 0, count_j = 0, size = m + n;
        int end = m; 
        int p = 0;
        while(p < size){ //每个元素都遍历,p指向当前nums1需要同nums2比较的位置
            if(count_j >= n) break; //nums2已经merge完毕则结束
            if(count_i < m && nums1[p] <= nums2[count_j]){//nums1还没merge完毕，
                count_i++;
                p++;
            }
            else{
               if(count_i < m){//nums[1]还没全部遍历完毕才移动
                   move(nums1, p, end-1);//移动p之后的元素
               }
               nums1[p] = nums2[count_j]; //放到p这个位置
               count_j++;
               p++; 
               end++;//尾部编号+1
            }
        }
    }
    void move(vector<int>& nums, int start, int end) {
        for(int i = end; i >= start; --i){
            nums[i+1] = nums[i];
        }
    }

　　上述复杂度为O(n^2)。另一种想法是从尾部开始merge。两个指针分别指向两个数组的最后一个元素，将二者中大的数挪到nums1最后一个位置p=m+n-1,一直到p=0或者nums2已经全部放到nums1中了，则停止循环。

void merge(vector<int>& A, int m, vector<int>& B, int n) {
    int i = m - 1, j = n - 1;
    int p = m + n - 1;//最后一个位置
    while(p >= 0){
        if(j < 0) break;
        if(i >= 0 && A[i] >= B[j]){
            A[p] = A[i--];
        }
        else{
            A[p] = B[j--];
        }
        --p;      
    }
}

　　还可以利用上面提到到的Inplace Merge方法，将nums2的元素直接全部放到nums1尾部，然后调用InplaceMerge方法。

Merge Two Sorted List(#21)

　　问：将两个有序链表merge到一起。
　　答：一种思路是将list2 Merge到list1，不断重新构造list1即可。如下：

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    if(l1 == NULL) return l2;
    if(l2 == NULL) return l1;
    
    if(l1->val > l2->val){//交换，保证l1的第一个数比l2的第一个数小
        ListNode *t = l1;
        l1 = l2;
        l2 = t;
    }
    
    ListNode *p = l1, *pre = l1, *q = l2;
      
    while(p != NULL || q != NULL){
        if(p == NULL){//l1已经到头了
            pre->next = q;
            break;
        }
        if(q == NULL) break;//l2已经全部merge完毕了
        
        if(p->val <= q->val){
            pre = p;
            p = p->next;
        }else{
            ListNode *tmp = q->next; 
            q->next = p;
            pre->next = q;
            pre = pre->next;//移动
            q = tmp;//移动
        }
    }
    return l1;
}

　　还有种方法是，新建一条新的链表，这个空间复杂度实际上是O(1),除了浪费一个头节点以外，其余的节点都是list1和list2上已经存在的节点。

ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    ListNode dump = ListNode(INT_MAX);
    ListNode *tail = &dump;
    while(l1 != NULL && l2 != NULL){
        if(l1->val <= l2->val) {
            tail->next = l1;
            tail = tail->next;
            l1 = l1->next;
        }else{
            tail->next = l2;
            tail = tail->next;
            l2 = l2->next;
        }   
    }
    tail->next = (l1 == NULL)? l2:l1;
    return dump.next;
}

Merge Two Binary Trees(#617)

　　问题：将两个二叉树Merge起来，如果位置相同则数据相加，否则添加该节点到新树上。如下图：

　　分析：显然这题需要使用递归操作。我们目标是将Tree2 Merge到Tree1上。首先，任意一棵树为NULL，则返回令一颗树即可，都不为空，则val相加，然后递归调用merge两棵树的左子树，merge两棵树的右子树。merge左子树时，如果Tree1的左子树为空，则需要将Tree2的左子树接到Tree1的左子树上。merge右子树时，如果Tree1的右子树为空，则需要将Tree2的右子树接到Tree1的右子树上。

struct TreeNode {
      int val;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
    if(t1 == NULL && t2 == NULL) return NULL;
    if(t1 == NULL && t2 != NULL) return t2;
    if(t1 != NULL && t2 == NULL) return t1;
    
    t1->val += t2->val;
    
    mergeTrees(t1->left, t2->left);//左子树merge
    if(t1->left == NULL){
        t1->left = t2->left;
    }
    
    mergeTrees(t1->right, t2->right);//右子树merge
    if(t1->right == NULL){
        t1->right = t2->right;
    }
    
    return t1;
}

Hamming Distance(#461)

　　问题：求两个序列的汉明码距离。
　　分析：汉明码距离就是二进制相应位置上不同数的总数。比如 0001和0100，第2位和第4位不同，则距离为2。求解很简单，两个数求异或。然后求异或结果的1的个数即可。

/* 先异或操作，然后统计1的个数。*/
   int hammingDistance(int x, int y) {
       int z = x ^ y; // xor
       return count_not_zero_bits(z);
   }   
   /* 统计非零位的个数，也就是统计任意一个数的二进制表示中1的个数*/
   int count_not_zero_bits(int x){
       int count = 0;
       while(x){//x非零
           ++count;
           x &= (x-1); //关键，每次都会把最靠右边的1变成0。如果最右边为0,与之后肯定为0不变；如果最右边是1，减一为0，与之后就变成0了。 
       }
       return count;
   }