Week-3-For-Leetcode

　　Leetcode第三周总结。

Longest Palindromic Subsequence (#516)

　　问题：求最大回文子串的长度。例如:character,最大回文子串长度为：len(carac)=5
　　分析：显然需要使用动态规划。按照动态规划三部曲:
1）首先观察最优解的特征。”carac”，首尾相等字符，显然只需要观察”ara”即可。如果是aract, 首尾字符不相等，那么a可能和最右边t左边的字符存在相等，t也可能和最左边a的右边的字符相等，因此最长回文只可能在”arac”和”ract”取到。
2）递归观察最优解值。要求character，首尾字符不相等，因此需要解”characte”和”haracter”,针对”characte”,又要解”charact”和”haracte”。可以发现长度是不断减小的。根据1中的观察，可以发现令dp[i,j]为序列i..j的最长回文子串，则dp[i,j] = dp[i+1,j-1],if s[i]=s[j]; dp[i,j] = max(dp[i+1,j], dp[i,j-1])，if s[i]!=s[j].
3）自底向上求解最优解。根据2）中观察，一种求解顺序方式可以按照长度来解子问题。另一种方式，可以发现dp[i,j]依赖于dp[i+1,j-1],dp[i+1,j], dp[i,j-1], 因此起始点i需要从序列的右端开始遍历,j需要从大于i的左端开始遍历。因此可以得到两种方式的的子问题求解顺序。归纳得到如下三幅图的求解顺序：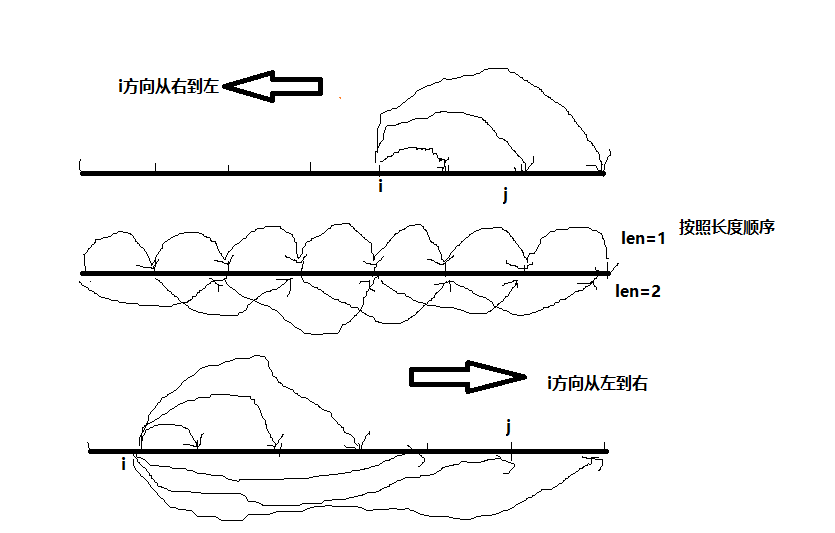

　　该题采用的是第一种和第二种方式。很多问题也可以采用第三种的求解顺序。
　　第一种方式，右端起点：

int longestPalindromeSubseq(string s) {
    int len = s.size();
    if(len == 0) return 0;
    vector<vector<int>> dp(len, vector<int>(len, 0));// i > j ,dp[i][j] = 0
    for(int i = 0; i < len; ++i){
        dp[i][i] = 1;
    }
    for(int i = len-1; i >= 0; --i){//起始点从右端开始
        for(int j = i+1; j < len; ++j){//终点
            if(s[i] == s[j]){
                dp[i][j] = dp[i+1][j-1] + 2;
            }else{
                dp[i][j] = max(dp[i+1][j], dp[i][j-1]);
            }
        }
    }
    return dp[0][len-1];
}*/

　　第二种方式，按照长度：

// 按照长度顺序来求解子问题也是可以的
int longestPalindromeSubseq(string s) {
    int len = s.size();
    if(len == 0) return 0;
    vector<vector<int>> dp(len, vector<int>(len, 0));// i > j ,dp[i][j] = 0
    for(int i = 0; i < len; ++i){
        dp[i][i] = 1;
    }
    for(int i = 2; i <= len; ++i){//i代表长度
        for(int start = 0; start <= len - i; ++start){//终点 end<=len-1 => start <= len - i
            int end = start + i - 1; 
            if(s[start] == s[end]){
                dp[start][end] = dp[start+1][end-1] + 2;
            }else{
                dp[start][end] = max(dp[start+1][end], dp[start][end-1]);
            }
        }
    }
    return dp[0][len-1];
}

　　拓展，如果要得到“最长回文子串”，要怎么处理？可以根据dp状态转移方程，如果s[i]=s[j]，则加入该字符，递归求解序列s[i+1,j-1]；否则根据dp[i+1,j]和dp[i][j-1]的大小，决定递归子序列s[i+1,j]还是s[i,j-1]。另外，处理上只需要保存回文串左半边的字符，右半边的字符等递归全部结束后根据左半边进行补全，对于左半边的最后一个字符需要判断是单独存在还是成对存在的。

string get_longest_palindrome_subseq(string &s, vector<vector<int>> &dp, int len){
        string result;
        bool is_last_single = false;
        longest(s, dp, 0, len-1, result, is_last_single);//先只放左半边
        
        //判断左半边最后一个元素是否是单独出现的
        int half_len = result.size()-1;
        if(!is_last_single){//如果最后一个不是单独的，则添加
            result.push_back(result[result.size()-1]);
        }
        
        //构建另一半
        for(int i = half_len-1; i >= 0; --i){
            result.push_back(result[i]);
        }
        return result;
    }

    void longest(string &s, vector<vector<int>> &dp, int i, int j, string &result, bool &is_last_single){
        if(i > j) return;
        if(s[i] == s[j]){
            result.push_back(s[i]);
            is_last_single = (i==j);//i=j时，最后被更新成true 
            longest(s, dp, i+1, j-1, result, is_last_single);
        }else{
            if(dp[i+1][j] >= dp[i][j-1]){
                longest(s, dp, i+1, j, result, is_last_single);
            }else{
                longest(s, dp, i, j-1, result, is_last_single);
            }
        }
        
    }

Different Ways to Add Parentheses (#241)

　　问：给定一个算术序列，求不同的加括号方式，求解总共有多少种答案。例如2-1-1={(2-1)-1=0, 2-(1-1)=2}.
　　答：该题类似“矩阵乘法加括号的动态规划问题”。求解某个序列的时候，可以遍历所有符号，然后按照某个符号左侧所有解，右侧所有解，左右两两组合得到该序列所有解。而某个大的序列求解依赖于小的序列，因此需要使用动态规划。注意，某个数字的长度不仅仅是1，比如21-1-1，第一个数长度为21。dp如果采用数组的话，需要使用三维的，因为dp[i][j](i序列左端，j序列右端）的值需要保存所有可能的解。本题使用的是哈希表，键存储该字符串序列，值存放所有可能的解。
　　法1：备忘录形式的递归算法。

vector<int> diffWaysToCompute(string input) {
        unordered_map<string, vector<int>> note;
        return compute(input, 0, input.size()-1, note); //备忘录法
    }*/
    // 2 * 3 - 4 * 5    2*[ -5, -17] = -10,-34;     6 - 20=-14    [2,-2]*5=10 -10
    // 按照符号划分成左侧和右侧。
    //备忘录法
    vector<int> compute(string& input, int low, int high, unordered_map<string, vector<int>> &note){
        string s = input.substr(low, high-low+1);
        if(note.find(s) != note.end()){
            return note[s];
        }
        vector<int> result;
        if(is_single_value(s)){//该序列只有1个值
            result.push_back(atoi(s.c_str()));
            note[s] = result;
            return result;
        }
        for(int k = low; k <= high; k++){
            if(is_opr(input[k])){
                vector<int> left = compute(input, low, k-1, note);
                vector<int> right = compute(input, k+1, high, note);
                for(int i = 0; i < left.size(); ++i){
                    for(int j = 0; j < right.size(); ++j){
                        int d = calculate(input[k], left[i], right[j]);
                        result.push_back(d);
                    }
                }     
            }
        }
        note[s] = result;
        return result;
    
    }
    int calculate(char opr, int s, int e){
        if(opr == '+') return s+e;
        if(opr == '-') return s-e;
        if(opr == '*') return s*e;
    }
    inline bool is_opr(char c){
        return (c == '+') || (c == '-') || (c == '*'); 
    }
    bool is_single_value(string &s){
        for(int i = 0; i < s.size(); ++i){
            if(is_opr(s[i])) return false;
        }
        return true;
    }

　　dp，按照序列的数字的个数，也就是长度顺序求解，如前文图中的中间那幅。

    //dp
vector<int> diffWaysToCompute(string input) {
    unordered_map<string, vector<int>> dp;
    int num = count_num(input);
    int start = 0;
    //初始化长度为1
    while(1){//end不好确认的时候，使用while
        int end = get_len_num_end(input, start, 1);
        if(end == -1) break;
        string s = input.substr(start, end-start+1);
        vector<int> result;
        result.push_back(atoi(s.c_str()));
        dp[s] = result;
        start = end + 2;//一个数的时候
    }
    
    for(int len = 2; len <= num; ++len){
        int start = 0;
        while(1){
            int end = get_len_num_end(input, start, len);//len的结尾
            if(end == -1) break;
            vector<int> result;
            for(int i = start; i <= end; ++i){
                if(is_opr(input[i])){
                    string l = input.substr(start, i-start), r = input.substr(i+1, end-i);
                    vector<int> left = dp[l], right = dp[r];
                    for(int x = 0; x < left.size(); ++x){
                        for(int y = 0; y < right.size(); ++y){
                            int d = calculate(input[i], left[x], right[y]);
                            result.push_back(d);
                        }
                    }  
                }
            }
            dp[input.substr(start, end-start+1)] = result;
            start = get_len_num_end(input, start, 1) + 2; ////移动到下一个数，比如21-1-1，len=2时;第一次,21-1,移动到21的结尾（数长度不止1）。
        }     
    }
    return dp[input];
}

int calculate(char opr, int s, int e){
    if(opr == '+') return s+e;
    if(opr == '-') return s-e;
    if(opr == '*') return s*e;
}
inline bool is_opr(char c){
    return (c == '+') || (c == '-') || (c == '*'); 
}
     
int get_len_num_end(string &s, int low, int len){
    if(low > s.size()-1) return -1;
    int c = 0;//1-1
    for(int i = low; i < s.size(); ++i){
        if(is_opr(s[i])){c++;}
        if(c == len) return i-1;
    }
    if(++c == len) return s.size()-1;
    return -1;
}

int count_num(string &s){
    int c = 0;
    for(int i = 0; i < s.size(); ++i){
        if(is_opr(s[i])){c++;}
    }
    return c+1;
}

Kth Largest Element in an Array(#\215)

　　问：找出数组第k大的数。
　　答：先转成求第k小的数。约定下，最小的数k=1;最简单的方法,使用partition,统计pivot左边(包括pivot)的数据个数c，c等于k则返回pivot,k小于c则递归求解左半边,否则递归右半边，适当修改下k的值即可。pivot的选择直接导致问题的复杂度，最坏的时候，T(n)=T(n-1)+O(n),T(n)=O(n^2)。一种方式是将数据5个5个分组，求每组的中位数，再求中位数的中位数，作为pivot。该解最差情况是\(T(n)=T(\frac{7}{10}n) + O(n)\), 解得T(n)=O(n)。\(\frac{7}{10}\)是因为，总共有n/5个中位数，中位数中有一半小于中位数的中位数，即n/5/2,这一半的中位数，每个都有3个数小于等于(或大于等于)该数，则有(n/5/2)*3=3/10个数一定小于等于(或大于等于)该pivot。因此可以过滤掉3/10的数。\(frac{n}{2m} * (\frac{m}{2}+1) \), m为每组的数量，上式是可以过滤掉的数据的占比。

//法1 
int quickSelect(vector<int>&nums, int low, int high, int k){            
    int mid = partition(nums, low, high);
    int m = mid - low + 1;//必须统计<=nums[mid]的个数
    if(k == m) return nums[mid];
    if(k < m){
        return quickSelect(nums, low, mid-1, k);
    }else{
        return quickSelect(nums, mid+1, high, k-m); 
    }
}
int partition(vector<int>&nums, int low, int high){
    int pivot = nums[high];//最后一个数作为pivot
    int i = low;//赋值成low
    for(int j = low; j < high; ++j){
        if(nums[j] <= pivot){ //统计小于等于i的位置，大于不动
            swap(nums, i, j);
            ++i;
        }
    }
    swap(nums, i, high);
    return i;
}
void swap(vector<int>& nums, int i, int j){
    int t = nums[i];
    nums[i] = nums[j];
    nums[j] = t;
}

　　法2：选择中位数的中位数。

void insertionSort(vector<int>& a, int l, int r){
    for(int i = l+1; i <= r; ++i){
        int t = a[i];
        int j = i-1; 
        while(j >= l && a[i] < a[j]){--j;}
        for(int k = i; k > j+1; --k){
            a[k] = a[k-1];
        }
        a[j+1] = t;
    }
}


int partition(vector<int>&nums, int low, int high,int pivot_index){
    swap(nums, high, pivot_index);//pivot交换到high
    int pivot = nums[high];
    int i = low;
    for(int j = low; j < high; ++j){
        if(nums[j] <= pivot){ 
            swap(nums, i, j);
            ++i;
        }
    }
    swap(nums, i, high);
    return i;
}
    
//法3:中位数的中位数,最小的数k=1
int BFPRT(vector<int>& a, int low, int high, int k){
    int n = high - low + 1; 
    if (n <= 5){ //小于等于5个数，直接排序得到结果，临界一定要注意
        insertionSort(a, low, high); 
        return a[low + k - 1]; //l+id-1
    }
    //此时已经保证n>5了。
    int t = low;//记录数组前面
    for(int i = 0; i < n/5; ++i){//分组
        int start = low + i*5;
        insertionSort(a, start, start + 4);
        swap(a, t++, start+2); //将中位数start+2替换到数组前面，便于递归求取中位数的中位数
    }

    int pivot_index = (low + t) / 2; //l到t的中位数的下标，作为主元的下标
    
    BFPRT(a, low, t, pivot_index-low+1);//一定要记得减去low
    
    int mid = partition(a, low, high, pivot_index);
    int m = mid - low + 1;
    if (k == m) return a[mid];                   //刚好是第id个数
    else if(k < m){
        return BFPRT(a, low, mid-1, k);//第id个数在左边
    }
    else{
        return BFPRT(a, mid+1, high, k-m);         //第id个数在右边
    }
}

　　另外还有构建最大堆求解的，建堆复杂度为logn,则求第k大的数复杂度为klogn.k很小的时候比较有优势。

//使用堆来实现
int findKthLargest(int* nums, int numsSize, int k) {
    build_max_heap(nums, numsSize);
    int result = 0;
    //O(k*logn)
    while(k){
        result = nums[0];
        swap(nums, 0, numsSize-1);
        --numsSize;//堆大小减少1
        max_heapify(nums, 0, numsSize);//维护堆
        --k;
    }
    return result;
}

inline int left(int idx){
   return (idx << 1) + 1;    
}
inline int right(int idx){
   return (idx << 1) + 2;    
}

inline void swap(int *nums, int i, int j){
    int t = nums[i];
    nums[i] = nums[j];
    nums[j] = t;
}

void max_heapify(int* nums, int idx,int heap_size){
    int largest = idx;
    int l = left(idx), r = right(idx);
    if(l < heap_size && nums[l] > nums[largest]) largest = l;
    if(r < heap_size && nums[r] > nums[largest]) largest = r;
    if(largest != idx){
        swap(nums, idx, largest);
        max_heapify(nums, largest, heap_size);
    }
}

//2x+1 < n   2x+2 < n 子孩子下标都<n
//x < (n-1)/2  n/2-1/2  x < (n-2)/2  n/2-1 -> x < n/2 -1 
void build_max_heap(int* nums, int heap_size){
    for(int i = heap_size/2-1; i >= 0; --i){
        max_heapify(nums, i, heap_size);
    }
}

//法2：优先队列法
priority_queue<int> pq(nums.begin(),nums.end());
for(int i = 0; i < k-1; ++i){
    pq.pop();
}
return pq.top();

求割点

　　dfs求割点。同时需要注意使用的是链表法构图。

#include <iostream>
#include<vector>
#include<algorithm>
using namespace std;

#define MAXVEX 100
typedef char VertexType; //顶点数据类型
typedef int EdgeType; //边上权重


//边结构  -----edge--->adjvex   类似这样的结构
struct EdgeNode {
    int adjvex;//前一个顶点经过该条边和该顶点连接，adjvex指的是该顶点的下标.弧尾
    EdgeType weight;//边权重
    EdgeNode *next;//指向下一条边
    EdgeNode() :next(NULL) {}
};

//顶点结构 
typedef struct VertexNode 
{
    VertexType data;//顶点数据域
    EdgeNode *firstedge;//顶点指向的第一条边
    VertexNode():firstedge(NULL){}
}AdjList[MAXVEX];


struct GraphAdjList {
    AdjList asjList;
    int numNodes;
    int numEdges;
};



//创建边节点 --weight-->j
EdgeNode *createEdgeNode(EdgeType weight, int j) {
    EdgeNode *e = new EdgeNode(); // EdgeNode e;是在栈上分配，不能返回引用。因为会销毁
    e->weight = weight;
    e->adjvex = j;
    e->next = NULL;
    return e;
}

//从顶点数组中 下标为i的顶点插入新的边e
void linkEdgeNode(GraphAdjList* G, int i, EdgeNode *e) {
    //头插入法
    //e->next = G->asjList[i].firstedge;//头插入法
    //G->asjList[i].firstedge = e;//挪向新的位置

    //尾插入法
    EdgeNode* p = G->asjList[i].firstedge;
    if (p == NULL) { G->asjList[i].firstedge = e; return; }
    while (p->next) {
        p = p->next;
    }
    p->next = e;
}


void createGraph(GraphAdjList* G) {
    int i, j, k;
    EdgeType weight;
    cin >> G->numNodes >> G->numEdges;

    for (i = 0; i < G->numNodes; ++i) {//i是顶点编号
        //cin >> G->asjList[i].data;
        G->asjList[i].firstedge = NULL;
    }

    for (k = 0; k < G->numEdges; ++k) {
        cin >> i >> j >>weight; // i---weight->j
        
        EdgeNode *e = createEdgeNode(weight, j);
        linkEdgeNode(G, i, e);
        
        //无向图
        e = createEdgeNode(weight, i);
        linkEdgeNode(G, j, e);
        
    }
}



void printGraphAdjList(GraphAdjList *G) {
    for (int i = 0; i < G->numNodes; ++i) {
        cout << i;//输出顶点头下标
        EdgeNode *p = G->asjList[i].firstedge;
        while (p) {
            cout << "----->" << p->adjvex;
            p = p->next;
        }
        cout << endl;
    }
}


vector<int> dfn(MAXVEX,0);
vector<int> parent(MAXVEX, -1);
vector<int> low(MAXVEX, 0);
int num = 0;

void dfs(GraphAdjList* G, int u) {
    dfn[u] = low[u] = ++num;
    EdgeNode *p = G->asjList[u].firstedge;
    int children = 0;
    while (p) {
        children++;
        int v = p->adjvex;
        if (dfn[v] == 0) {//未遍历
            parent[v] = u;//在if里面设置
            dfs(G, v);
            low[u] = min(low[u], low[v]);

            if (parent[u] == -1 && children >= 2) {// 如果是根节点且有两棵以上的子树则是割点
                cout << "Articulation point: " << u << endl;;
            }
            //只要有一个子节点的low值大于它就是割点了
            if (parent[u] != -1 && low[v] >= dfn[u]) { //不是根节点
                cout << "Articulation point: " << u << endl;
            }
        }
        else if(parent[v] != u){// 余边，v之前已经遍历了
            low[u] = min(low[u], dfn[v]);   
        }
        p = p->next;
    }
}

int main() {
    GraphAdjList g;
    createGraph(&g);
    printGraphAdjList(&g);
    dfs(&g, 1);
    system("pause");
}

Unique Paths(#62)

　　机器人从左上角到右下角，只能往下和往右走，问有多少条路径。

//dp 从右下角开始求解，dp[i][j] = dp[i+1][j] + dp[i][j+1];
int uniquePaths(int m, int n) {
    vector<vector<int>> dp(m+1, vector<int>(n+1));
    for(int j = 1; j <= n; ++j){
        dp[m][j] = 1;
    }
    for(int i = 1; i <= m; ++i){
        dp[i][n] = 1;
    }
    for(int i = m-1; i >= 1; --i){
        for(int j = n-1; j >= 1; --j){
            dp[i][j] = dp[i+1][j] + dp[i][j+1];
        }
    }
    return dp[1][1];
}

Edit Distance(#72)

　　问：给定两个字符串，使用增删改的方式，将word1转换成word2最少的步数是多少。
　　答：例如将algorithm转成altruistic。使用动态规划法，递归观察最优解形式，dp[i,j]记录的是word1从[0..i]变成word2[0..j]的编辑距离。使用不同操作，状态转移方程不一样。考察最后一个字符,如果采用增加的方式，则word1变成algorithmc,则dp[i,j]=dp[i,j-1]+1,即需要考察子问题,algorithm变成altruisti；如果采用删除的方式，则dp[i,j]=dp[i-1,j]+1,即考察子问题，algorith变成altruistic；如果采用替换的方式，则dp[i,j]=dp[i-1,j-1] + {0或者1}, 即考察子问题，algorith变成altruisti。+0还是1根据word1[i]和word[j]是否相等来决定。因此dp[i,j]依赖于dp[i-1,j],dp[i,j-1],dp[i-1][j-1],本题求解子问题顺序和求最长公共子序列一样。

int minDistance(string word1, string word2) {
    int m = word1.size(), n = word2.size();
    vector<vector<int>> dp(m+1, vector<int>(n+1));
    for(int i = 0; i <= m; ++i){//i代表word1字符个数
        dp[i][0] = i;
    }
    for(int j = 0; j <= n; ++j){//j代表word2字符个数
        dp[0][j] = j;
    }
    
    for(int i = 1; i <= m; ++i){
        for(int j = 1; j <= n; ++j){
            int d = (word1[i-1] != word2[j-1]); //word中下标是从0开始的，不相等的时候d=1
            dp[i][j] = min(min(dp[i][j-1] + 1, dp[i-1][j] + 1), dp[i-1][j-1] + d);// 依次是insert delete replace
        }
    }
    return dp[m][n];      
}