K-means和混合高斯模型

　　本文主要的内容包括：无监督学习中的K均值(k-means)聚类算法、混合高斯分布模型(Mixture of Gaussians, MoG)、求解MoG模型的期望最大化(EM)算法，以及EM一般化形式。

k-means算法

　　在聚类问题中，给定一组数据$\{x^{(1)},…,x^{(m)}\}$，$x^{(i)} \in \mathbb{R}^n$，但是未给标签$y^{(i)}$。因此这是个无监督学习问题，需要聚类算法去发掘数据中的隐藏结构。

算法

　　k-means算法的具体流程如下：

• 1）随机初始化k个聚类中心$\mu_1,\mu_2,…,\mu_k \in \mathbb{R}^n$
• 2）为每个样本数据选择聚类中心，即将其类别标号设为距离其最近的聚类中心的标号：
  $$c^{(i)}:=arg \min_j ||x^{(i)}-\mu_j||^2$$
• 3）更新聚类中心，即更新为属于该聚类中心的所有样本的平均值：
  $$\mu_j=\frac{\sum_{i=1}^m I\{c^{(i)}=j\}x^{(i)}}{\sum_{i=1}^m I\{c^{(i)}=j\}}$$
• 4）重复2、3步骤，直到聚类中心不变或变化低于阈值为止。

　　在上述问题中，k是k-means算法的参数，是聚类中心的数量。$\mu_j$代表目前对某个聚类中心的猜测。为了初始化聚类中心，我们可以随机选取k个训练样本作为聚类中心初始值。下图是k=2时的一个聚类算法演示过程：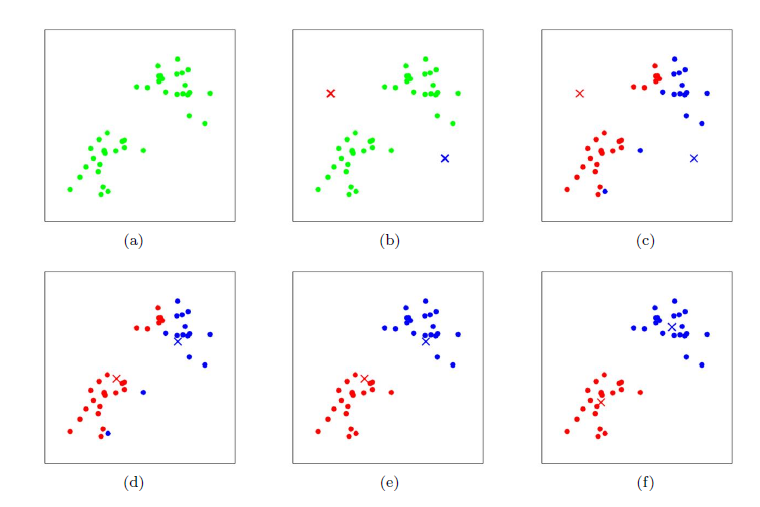

优化函数

　　聚类算法能够保证收敛吗？我们定义k-means的优化函数为：
$$J(c,\mu)=\sum_{i=1}^m ||x^{(i)}-\mu_{c^{(i)}}||^2$$
　　$J$衡量了每个样本距离其中心的距离平方和。可以将k-means算法看作是目标函数J的坐标下降(coordinate descent，在SVM中SMO算法中介绍过)过程。在第2步中，我们保持聚类中心不变，将样本类别设为距离最近的中心的类别，此时对于修改了类别中心的样本，其距离的平方会变小，即$\sum_{修改类别的样本}||x-\mu||^2$的值变小，而没有修改类别的样本J不变，从而整体变小。在第三步中，我们保持样本类别不变，更新了聚类中心点的值，这样使得对每个类别而言，其目标函数项会变小，即$\sum_{属于某类的样本}||x-\mu||^2$变小，从而整体变小。因此$J$会不断减小，从而保证收敛，通常这也意味着$c、\mu$也会收敛。理论上，不同的聚类中心可能会导致相同的收敛值J，称作震荡。但在实际中很少发生。
　　上述目标函数$J$是非凸的(non-convex)，因此坐标下降法不能保证收敛到全局最优值，容易陷入局部最优值。一个较为简单的解决方法是随机初始化多次，以最优的聚类结果(即J最小)为最终结果。
　　在聚类结束后，如果一个中心没有得到任何样本，那么需要去除这个中心点或者重新初始化。
　　聚类算法可用于离群点检测。比如飞机零件评测、信用卡消费行为异常监控等。

混合高斯分布

　　混合高斯分布(MoG)也是一种无监督学习算法，常用于聚类。当聚类问题中各个类别的尺寸不同、聚类间有相关关系的时候，往往使用MoG更合适。对一个样本来说，MoG得到的是其属于各个类的概率(通过计算后验概率得到)，而不是完全的属于某个类，这种聚类方法被称作软聚类。一般来说，任意形状的概率分布都可以用多个高斯分布函数取近似，因而MoG的应用比较广泛。

形式化表述

　　在MoG问题中，数据属于哪个分布可以看成是一个隐含变量$z$。与k-means的硬指定不同，我们首先认为$z^{(i)}$满足一定的概率分布，并使用联合概率分布来进行建模，即:$p(x^{(i)},z^{(i)})=p(x^{(i)}|z^{(i)})p(z^{(i)})$。其中，$z^{(i)} \sim Multinomial(\phi)$即z服从多项式分布($\phi_j \geq 0, \sum_{j=1}^k \phi_j=1,\phi_j=p(z^{(i)}=j)$)。$x^{(i)}|z^{(i)} \sim \mathcal{N}(\mu_j,\Sigma_j)$,即在给定z的条件下，x服从高斯分布。令$k$为$z^{(i)}$取值范围的数量。MoG模型假设每个$x^{(i)}$的产生有两个步骤，首先从k个类别中按多项式分布随机选择一个$z^{(i)}$，然后在给定$z^{(i)}$条件下，从k个高斯分布中选择使得联合概率最大的高斯分布，并从该分布中生成数据$x^{(i)}$。
　　(注意：学习一个模型的关键在于理解其数据产生的假设。后面学习因子分析模型时，也要重点关注其数据产生的假设(低维空间映射到高维空间,再增加噪声)，这是上手的突破口。)
　　因此我们模型的参数是:$\phi,\mu,\Sigma$，为了估计这些参数，我们写出似然函数：
$$\mathcal{l}(\phi,\mu,\Sigma)=\sum_{i=1}^m log \ p(x^{(i)};\phi,\mu,\Sigma) \\\ = \sum_{i=1}^m log \ \sum_{z^{(i)}=1}^k p(x^{(i)}|z^{(i)};\mu,\Sigma)p(z^{(i)};\phi)$$
　　由于$z^{(i)}$是未知的，如果对上述求导并设为0来求解问题，会很难求解出最大似然估计值。
　　随机变量$z^{(i)}$指明了每个样本x^{(i)}到底是从哪个高斯分布生成的。如果$z^{(i)}$已知，则极大似然估计就变得很容易，重写为：
$$\mathcal{l}(\phi,\mu,\Sigma) = \sum_{i=1}^m log \ \sum_{z^{(i)}=1}^k p(x^{(i)}|z^{(i)};\mu,\Sigma)+log \ p(z^{(i)};\phi)$$
　　求导得到极大似然估计结果为：
$$\phi_j=\frac{1}{m}\sum_{i=1}^m I\{z^{i}=j\}\\\\ \mu_j=\frac{\sum_{i=1}^m I\{z^{i}=j\}x^{(i)}}{\sum_{i=1}^m I\{z^{(i)}=j\}}\\\\ \Sigma_j=\frac{\sum_{i=1}^m I\{z^{(i)}=j\}(x^{(i)}-\mu_j)(x^{(i)}-\mu_j)^T}{\sum_{i=1}^m I\{z^{(i)}=j\}}$$
　　实际上，如果$z^{(i)}$的值已知，那么极大似然估计和之前生成算法中的GDA很类似，这里的$z^{(i)}$就相当于生成算法的类标签。所不同的是，GDA里的y是伯努利分布，而这里的z是多项式分布，并且每个样例有不同的协方差矩阵，而GDA中认为只有1个。
　　然而在我们的问题中，$z^{(i)}$是未知的，该如何解决？

EM算法和混合高斯模型

　　最大期望算法是一种迭代算法，主要有两个步骤。在我们的问题中，第一步E-step，尝试猜测$z^{(i)}$的值；第二步M-step,基于猜测，更新模型参数的值。
　　循环下面步骤，直到收敛：{
　　　　E：对于每个i和j,计算(即对每个样本i，计算由第j个高斯分布生成的概率，每个高斯分布代表一种类别，也就是z的分布):
$$w_j^{(i)}:= p(z^{(i)}=j|x^{(i)};\phi,\mu,\Sigma)=\frac{p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)p(z^{(i)}=j;\phi)}{\sum_{l=1}^k p(x^{(i)}|z^{(i)}=l;\mu,\Sigma)p(z^{(i)}=l;\phi)}$$
　　　　M: 更新参数：
$$\phi_j:=\frac{1}{m}\sum_{i=1}^m w_j^{(i)}$$
$$\mu_j := \frac{\sum_{i=1}^m w_j^{(i)}x^{(i)}}{\sum_{i=1}^m w_j^{(i)}}$$
$$\Sigma_j := \frac{\sum_{i=1}^m w_j^{(i)}(x^{(i)}-\mu_j)(x^{(i)}-\mu_j)^T}{\sum_{i=1}^m w_j^{(i)}}$$

　　在E步中，我们将其他参数$\Phi,\mu,\Sigma$看作常量，计算$z^{(i)}$的后验概率，也就是估计隐含类别变量。其中，$p(x^{(i)}|z^{(i)}=j;\mu,\Sigma)$根据高斯密度函数得到，$p(z^{(i)}=j;\phi)$根据多项式分布得到。因此$w_j^{(i)}$代表隐含类变量$z^{(i)}$的软估计。
　　在M步中，估计好后，利用上面的公式重新计算其他参数，$\phi_j$是多项式分布的参数，决定了样本属于第j个高斯分布的概率。因为每个样本都会计算属于不同高斯分布生成的概率，所以可根据每个样本属于第j个高斯分布的概率来求平均得到。$\mu_j,\Sigma$是高斯分布的参数。
　　计算好后发现最大化似然估计时，$w_j^{(i)}$的值又不对了，需要重新计算，周而复始，直至收敛。
　　ＥＭ算法同样会陷入局部最优化，因此需要考虑使用不同的参数进行初始化。 　　

一般化EM算法

　　上述EM算法是对于混合高斯模型的一个例子。到目前为止，我们还没有定量地给出EM的收敛性证明，以及一般化EM的推导过程。下面重点介绍这些内容。

Jensen不等式

　　若f为凸函数，即$f’’(x) \geq 0$。注意，并不要求f一定可导，但若存在二阶导数，则必须恒大于等于0。再令X为随机变量，则存在不等式:
$$f(E[X]) \leq E[f(x)]$$
　　进一步，若二阶导数恒大于0，则不等式等号成立当且仅当x=E[x],即x是固定值。
　　若二阶导数的不等号方向逆转，则不等式的不等号方向逆转。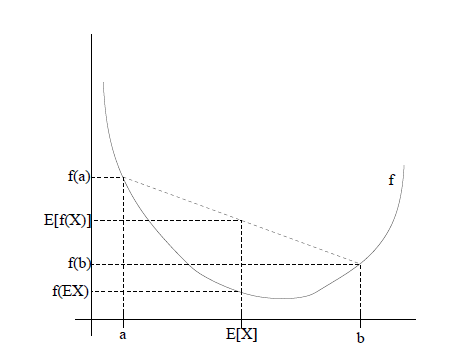

EM算法一般化形式

　　假设有一个训练集$\{x^{(1)},x^{(2)},…,x^{(m)}\}$,由m个独立的样本构成，我们的目标是拟合包含隐变量的模型$p(x,z)$,似然函数如下：
$$\ell (\theta)=\sum_{i=1}^m log p(x;\theta) \\\\ = \sum_{i=1}^m log \sum_{z^{(i)}} p(x,z;\theta)$$
　　直接对上式求导来求似然函数估计会非常困难。注意，这里的$z^{(i)}$是隐变量，并且和上面一样，如果$z^{(i)}$已知，那么似然估计很容易。但无监督算法中$z^{(i)}$未知。
　　在这种情况下，EM算法给出了最大似然估计的一种有效的求法。直接最大化$\ell$很困难。相反，我们通过构造$\ell$的下界(E-step)，并且最优化下界(M-step)来解决。
　　对每一个样本i，令$Q_i$为关于隐含变量z的分布,是一种概率($\sum_i Q_i(z)=1, Q_i(z) \geq 0$)
$$\sum_i log p(x^{(i)};\theta)=\sum_i log \sum_{z^{(i)}} p(x^{(i)},z^{(i)};\theta)\\\\ =\sum_{i} log \sum_{z^{(i)}} Q_i(z^{(i)})\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\\\\ = \sum_{i} log E\left[\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\right] \\\\ \geq \sum_{i} E\left[log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}\right] \\\\ = \sum_{i}\sum_{z^{(i)}} Q_i(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$
　　上面推导根据Jensen不等式，log函数二阶导函数小于0，因此是非凸的，故不等号逆转。
　　因此有：
$$\ell(\theta) \geq \sum_{i}\sum_{z^{(i)}} Q_i(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}=lowbound(\theta)$$
　　现在，对任意分布$Q_i$,$lowbound(\theta)$给出了$\ell(\theta)$的下界。$Q_i$的选择有很多种，我们该选择哪种呢? 假设目前已经求出了$\theta$的参数，我们肯定希望在$\theta$处使得下界更紧，最好能够使得不等式取等号。后面我们会证明，随着EM的迭代，$\ell$会稳步增加，逼近等号成立。
　　为了使得对于特定的$\theta$下界更紧，我们需要使得Jensen不等式取到等号。即$X=E[X]$时取到等号。当X为常数时，能够保证该条件成立。故令：
$$\frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)};\theta)}=c$$
　　通过选择合适的$Q_i(z^{(i)})$，能够使得c不受$z^{(i)}$的影响。可以选择$Q_i(z^{(i)})$满足下式：
$$Q_i(z^{(i)}) \propto p(x^{(i)},z^{(i)};\theta)$$
　　又因为，$\sum_{z^{(i)}} Q_i(z^{(i)})=1$,以及$Q_i(z^{(i)})=\frac{p(x^{(i)},z^{(i)};\theta)}{c}$
　　两边求和，
$$\sum_{z^{(i)}} Q_i(z^{(i)})=\sum_{z^{(i)}} \frac{p(x^{(i)},z^{(i)};\theta)}{c}=1$$
故， $$\sum_{z^{(i)}} p(x^{(i)},z^{(i)};\theta)=c$$
则： $$Q_i(z^{(i)})=\frac{p(x^{(i)},z^{(i)};\theta)}{c}=\frac{p(x^{(i)},z^{(i)};\theta)}{\sum_{z^{(i)}} p(x^{(i)},z^{(i)};\theta)}\\\\ =\frac{p(x^{(i)},z^{(i)};\theta)}{p(x^{(i)};\theta)} \\\\ =p(z^{(i)} | x^{(i)};\theta)$$
　　因此，只要令$Q_i$为给定$\theta^{(t)}$以及观察值x下，$z^{(i)}$的后验概率分布即可。
　　因此EM算法迭代过程如下：
　　E-step:对每一个样本i,令：
$$Q_i(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta^{(t)})$$
　　M-step,令：
　　 $$\theta^{(t+1)}:=arg \max_\theta \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$
　　如何保证算法的收敛性？假设$\theta^{(t)}$和$\theta^{(t+1)}$是连续两次EM算法迭代求得的参数值。我们可以证明：$\ell(\theta^{(t+1)}) \geq \ell(\theta^{(t)})$,这意味着随着迭代次数增加，最大似然值也在稳步增加。为了得到这样的结果，这里的关键在于Q的选择。假设EM算法初始参数值为$\theta^{(t)}$,选择$Q_i^{(t)}(z^{(i)}):=p(z^{(i)}|x^{(i)};\theta^{(t)})$.前面我们知道，这样的选择能够保证Jensen不等式等号成立，即使得$\ell$的下界最紧，根据前面，我们有：
$$\ell(\theta^{(t)})=\sum_i \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta^{t})}{Q_i^{(t)}(z^{(i)})}$$
进而：
$$\ell(\theta^{(t+1)}) \geq \sum_i \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta^{t+1})}{Q_i^{(t)}(z^{(i)})} \\\\ \geq \sum_i \sum_{z^{(i)}} Q_i^{(t)}(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta^{t})}{Q_i^{(t)}(z^{(i)})} \\\\ =\ell(\theta^{(t)})$$
第一个式子是根据前面的Jensen不等式：
$$\ell(\theta) \geq \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$
当$Q_i=Q_i^{(t)}$时，取到等号，此时$\theta=\theta^{(t+1)}$。
第二个式子通过极大似然估计得到$\theta^{(t+1)}$值，也就是M-step：
$$arg \max_\theta \sum_i \sum_{z^{(i)}} Q_i(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$
　　为了便于理解，这里以一幅图来对EM算法进行总结。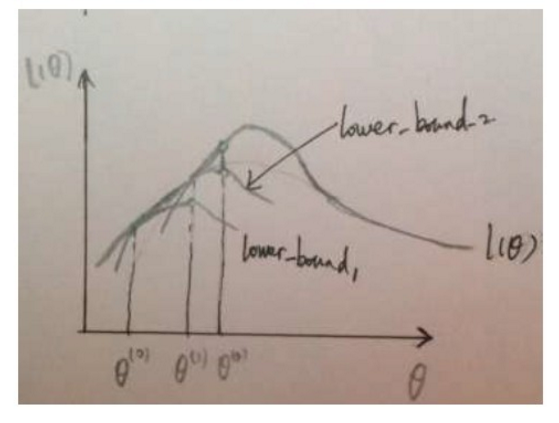

　　上述所展现的内容就是前面所述的主要思想，存在一个我们不能直接进行求导的似然函数，给定初始参数，我们找到在初始参数下紧挨着似然函数的下界函数，在下界上求极值来更新参数。然后以更新后的参数为初始值再次进行操作，这就是EM进行参数估计的方法。
　　当然似然函数不一定是图4中那样只有一个极值点，因而EM算法也有可能只求出局部极值。当然，可以像K-means那样多次选择初始参数进行求解，然后取最优的参数。
　　在EM的一般化形式中，可以将目标函数看作是：
$$J(Q,\theta)=\sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)})log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})}$$
　　这样，EM算法就可以看作是对目标函数的坐标上升过程。在E-step中，$\theta$不变，调整Q使函数变大；在M-step中，Q不变，调整$\theta$使目标函数变大。
　　实际上上述式子还可以进一步化简，上述式子改写为：
$$J(Q,\theta)=\sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)}) \left(log p(x^{(i)},z^{(i)};\theta) - log Q_i(z^{(i)})\right) \\\ = \sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)})*log p(x^{(i)},z^{(i)};\theta) - Q_i(z^{(i)})*log Q_i(z^{(i)})$$
　　由于第t步迭代下，$\theta_i$已知，因此Q_i(z^{(i)})可以在E-step中计算出来，这样在M-step时候就相当于常数了，因此优化的时候可以忽略上述$Q_i(z^{(i)})*log Q_i(z^{(i)})$常数项，则优化目标变成：
$$J(\theta)=\sum_{i=1}^m \sum_{z^{(i)}} Q_i(z^{(i)})*log p(x^{(i)},z^{(i)};\theta) \\\ = \sum_{i=1}^m \sum_{z^{(i)}} p(z^{(i)}|x^{(i)};\theta^{(t)})log p(x^{(i)},z^{(i)};\theta) \\\ = E_Z[log(X,Z|\theta)|X,\theta^{(t)}]$$
　　这也是统计学习方法中的优化目标定义。

参考

斯坦福大学机器学习视频教程
统计学习方法