Alpha Go论文解析

摘要

围棋游戏的挑战在于庞大的搜索空间、评估棋面局势和选择走子的困难。作者提出一种使用“价值网络”来评估棋面局势，使用“策略网络”来选择走子的方法。这些深度网络是通过结合人类专业围棋比赛的监督学习方法，以及自我对弈的强化学习方法进行训练的。作者还提出一种结合深度网络和蒙特卡罗搜索树的新方法。

思考
1) 为什么价值网络和策略网络要分开？二次很相似且有重叠，能否合并？
答：通过后续的阅读，我感觉这里设计两个网络的灵感来源可能在于，蒙特卡罗搜索树两个剪枝原则的设计和实
现，每个网络对应1个剪枝原则，后续会讨论。还有可能来自于DRL深度增强学习中Double 
Q-learning两个网络的启发。

2）深度网络的训练能否去除掉人类比赛的监督学习数据，而完全使用强化学习进行训练？
答：如果能，那我的疑惑在于，缺乏先验知识，2个6岁的小孩一直对弈能变成职业选手吗？

3）作者强调不使用"向前看几步的搜索策略“，即without any looking ahead search。蒙特卡罗搜索树
的搜索策略需要向前看走子才能评估每步的效益；而使用神经网络直接建模每个棋面状态下，所有合法动作上的
概率分布，这样可以直接计算出每个状态下的最优步。二者实际上各有优劣，深度网络能够更有效的评估当前棋
面局势，而蒙特卡罗搜索树向前看的方式能够预估后续棋步的局势。二者结合起来效果更优。后续将对此进一步讨论。
(Without any lookahead search, the neural networks play Go at the level of 
state-of-the-art Monte Carlo tree search programs that simulate thousands of 
random games of self-play)

研究现状

目前为止所有的棋类游戏都是为每个棋盘状态或每个棋面局势设计一个值函数，用于评估和判断该棋面局势。这个值函数是基于所有优秀棋手过往比赛的数据得到的。一种最基本的方法是递归穷举搜索树，总共有$b^d$ 种可能，其中$b$是搜索的宽度，即每个位置的合法的走子，$d$是搜索的深度，即总共有多少步。通常这样的穷举是不合理的，因为搜索空间实在太大。

可以通过两个原则对搜索空间进行约减得到有效的搜索空间。第一个原则是减少搜索的深度，可以通过“棋面局势评估”实现。也就是说使用近似的值函数来替换状态s（棋盘局势）下的子树，这个近似的值函数可以用于预测状态s下的输出，核心思想是直接计算得到下一步下法，没必要走到底才做出决策。第二个原则是减少搜索的宽度，使用策略分布$p(a|s)$（棋面s条件下，可能的走子动作）来随机采样下一步可能的action，也就是说将下一步搜索局限在那些高概率的动作，核心思想是决定分支节点如何有效转移。例如蒙特卡罗rollouts在策略p下，通过多次模拟采样棋手双方最长走子序列，平均所有的模拟过程来评估当前棋面下，采取不同动作的效益值。

目前这种方法通常只适用于浅层的、基于输入特征线性组合的值函数或策略函数。

思考
1）目前的方法是基于值函数计算每个棋面的效益值，直接挑选效益值大的下一步的位置进行走子。每次走子，将
当前棋面作为输入，输入到值函数中，值函数输出下一步的动作。通过下述论文的阅读，需要预测当前棋面下，
每一个可能的动作(也就是下一步走子的位置）的效益值，选择效益值最大的作为下一步动作。本文使用策略网络
来近似值函数，避免了looking ahead方式。

2）值函数具体是怎么设计和如何使用优秀棋手比赛数据训练的？
All games of perfect information have an optimal value function, v*(s), which 
determines the outcome of the game, from every board position or state s, 
under perfect play by all players.

3）搜索空间约减第一个原则通过近似的值函数替换状态s下的子树来达到减少深度。个人认为是为了减少向前看
的步数，正常的搜索是从该状态父节点转移到下一个子节点，再递归的对子节点做同样的操作，一直遍历到最后
一步，再回溯的计算该状态s的效益值。而这里使用一个值函数代替子树，也就相当于减少了递归的深度，直接使
用值函数作为叶子节点，用于计算该状态下的效益值。
First, the depth of the search may be reduced by position evaluation: 
truncating the search tree at state s and replacing the subtree below s by an 
approximate value function v(s) ≈ v*(s) that predicts the outcome from state s.

4）搜索空间约减的第二个原则是减少搜索的宽度，使用策略分布采样某个位置下可能的动作。这里主要目的是为
了控制搜索树的节点状态转移方向，将下一步转移动作局限在那些高概率的动作，忽略其他大量的低概率动作。
这样可以有效减少每个位置节点的分支数(宽度)。这里的问题在于这个策略分布如何训练得到的？

5）第二个原则，文中提到蒙特卡罗快速走子策略，原文如下，不是很理解这里maximum depth without 
branching at all的意思？我的理解是，蒙特卡罗为下棋程序以及人类对手都生成一个没有分支的单一走子
序列，这个序列的长度就是最大的树深度，可以理解为一直到决出胜负的那一步为止。然后对比这两种序列，在
所有可能的序列上进行平均，计算该状态位置s的效益值。
Monte Carlo rollouts search to maximum depth without branching at all, by 
sampling long sequences of actions for both players from a policy p. Averaging 
over such rollouts can provide an effective position evaluation。

6）后续我们会发现，融合深度神经网络的蒙特卡罗搜索树方法本质上也是从这两个思路出发，使用深度神经网络
来减小蒙特卡罗搜索空间。其中策略网络用于减小搜索的宽度，价值网络用于减小搜索的深度。
(这是不是也是设计两个网络的灵感来源？)

核心工作

目前，深度卷积神经网络在视觉领域取得了空前的成就。作者同样采取深度卷积神经网络，将19*19的棋盘看做是一个图像，输入到网络中，使用网络构建棋盘每个位置的表示。文章中采用两种卷积神经网络，值神经网络用于棋面局势评估，策略神经网络用于采样下一步动作，这两种网络能够有效减少搜索树的宽度和深度。

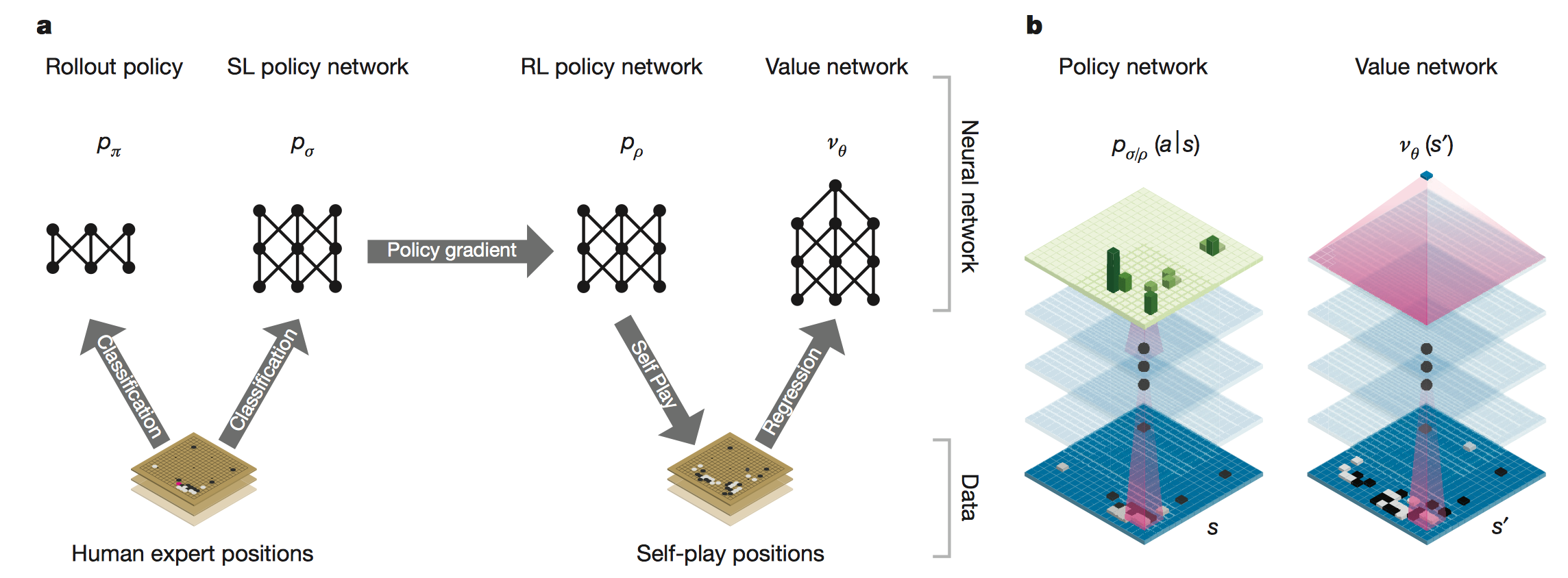
本文使用管道来组织和训练神经网络，管道由多个阶段的机器学习过程构成。首先构建一个监督学习策略网络$p_\sigma$, 训练数据来自人类专家棋手的比赛数据，学习的目标是建模专家在当前状态$s$下，下一步选择的下法(action)，$p_\sigma =p(a|s)$,这能够提供快速、有效的参数更新。同时，本文也训练一个快速走子策略$p_\pi$, 这个Rollout Policy可以在走子阶段快速采样下一步走法(action)。接着训练一个强化学习策略网络$p_\rho$，通过自我对弈，在监督学习网络$p_\sigma$最终学习结果基础上调整优化学习目标，这里的学习目标是赢棋，战胜监督学习策略网络。而原始的监督学习策略网络预测的是跟专家走法一致的准确率。在强化学习策略网络自我对弈过程中，会生成新的数据集。最后，训练一个价值网络，用于预测某个棋面局势下赢棋的概率。上述离线训练的策略网络和价值网络能够有效的和蒙特卡罗搜索树（MCTS）结合在一起，进而在线上进行比赛。

思考
1）监督学习策略网络训练目标是模仿人类专家棋手的下法，也就是在当前棋盘局势下，人类专家最可能怎么走。
而强化学习策略网络要跟该监督学习网络进行对抗，学习目标是战胜该监督学习网络，该监督学习网络间接得充
当了人类的角色。相当于是一个博弈的过程，程序首先使用监督学习策略网络预测人类专家想要最大化赢棋最可
能怎么走，再使用强化学习网络最小化人类专家赢棋可能性，也就是要战胜人类。总结起来相当于是一个minmax
博弈的过程。
A reinforcement learning (RL) policy network p ρ is initialized to the SL 
policy network, and is then improved by policy gradient learning to maximize 
the outcome (that is, winning more games) against previous versions of the 
policy network. A new data set is generated by playing games of self-play with 
the RL policy network.

2）价值网络用于预测某个棋面下赢棋的可能性，而强化学习策略网络目标是在某个棋面下决策下一步走法。价值
网络和强化策略网络学习目标实际上是很一致的，感觉这就是后面会被合并的原因吧？

3）怎么和MCTS结合在一起？上述的快速走子策略是不是就是用于MCTS过程?
答：是的。后续阅读发现快速走子策略用于蒙特卡罗搜索的评估阶段，和价值网络一起进行评估。

离线训练深度网络

这部分包括监督学习策略网络、快速走子策略、强化学习策略网络、价值网络四部分的训练。

监督学习策略网络$P_\sigma$

学习目的：预测专家在当前棋面下，下一步的走法，$P_\sigma = P(a|s)$。也就是下一步棋在棋盘上其它空地上的落子概率。核心目的是为了模仿人类专家下棋。
网络结构：13层卷积神经网络，非线性整流函数，使用softmax输出层。
网络输入：网络的单个输入是19*19棋面对应的黑白空三值图像，训练数据来源是30 million positions from the KGS Go Server，实际训练的时候是从这么多的棋局中随机抽取棋面（棋局某个时刻的局势）以及该棋面下，下一步动作的真实走法。构成棋面-动作对，$state-action pairs (s,a)$。注意这里面不需要棋局最终胜负标签。
网络输出：输出每一个合法动作$a$的概率分布$P(a|s)$，决策时可根据 $arg max_a P(a|s) $。
优化目标：最大化对数似然函数，$max log P_\sigma (a|s)$。随机梯度下降法进行参数更新：
$$
\Delta_\sigma \propto \frac{\partial log P_\sigma(a|s)}{\partial \sigma}
$$
验证评估：hold-out验证，即单独划分出一份测试集；使用所有的输入特征，包括棋盘位置，历史走子和围棋领域相关的全局特征（如“气“等），得到的正确率是57.0%；只使用棋盘位置和走子特征，得到的准确率是55.7%。作为对比，目前最前沿的研究结果是44.4%的正确率。
优缺点：正确率大幅度提升，但是搜索过程中，评估速度慢。

思考
1) 每个棋局都有黑白双方，AlphaGo训练的时候是站在哪一方进行的？还是说同时站在双方？我个人理解是站
在双方，因为任意一个棋面都能够知道接下来轮到谁来着棋(黑棋先手，数下当前黑白棋个数即可推出)
，因此构造训练数据标签时，就可以直接选择相应的棋方对应的下一步动作的走法。

2）这里测试验证的过程，我的理解是hold-out出部分【棋面和对应的下一步动作】，然后使用网络预测下一步
动作是什么，最后看看和该棋面对应的真实的下一步动作是否一致。为什么不用cross-validation,是不是因
为计算复杂度？

3）上述优化目标最大化对数似然，网络最后一层使用softmax激活，得到的是该棋面下不同动作的似然值。个
人认为，更新时，只使用【真实动作标签对应的似然值】来更新参数。若真实动作标签为1，其余动作标签为0，
则此处最大似然优化目标等价于交叉熵损失函数。

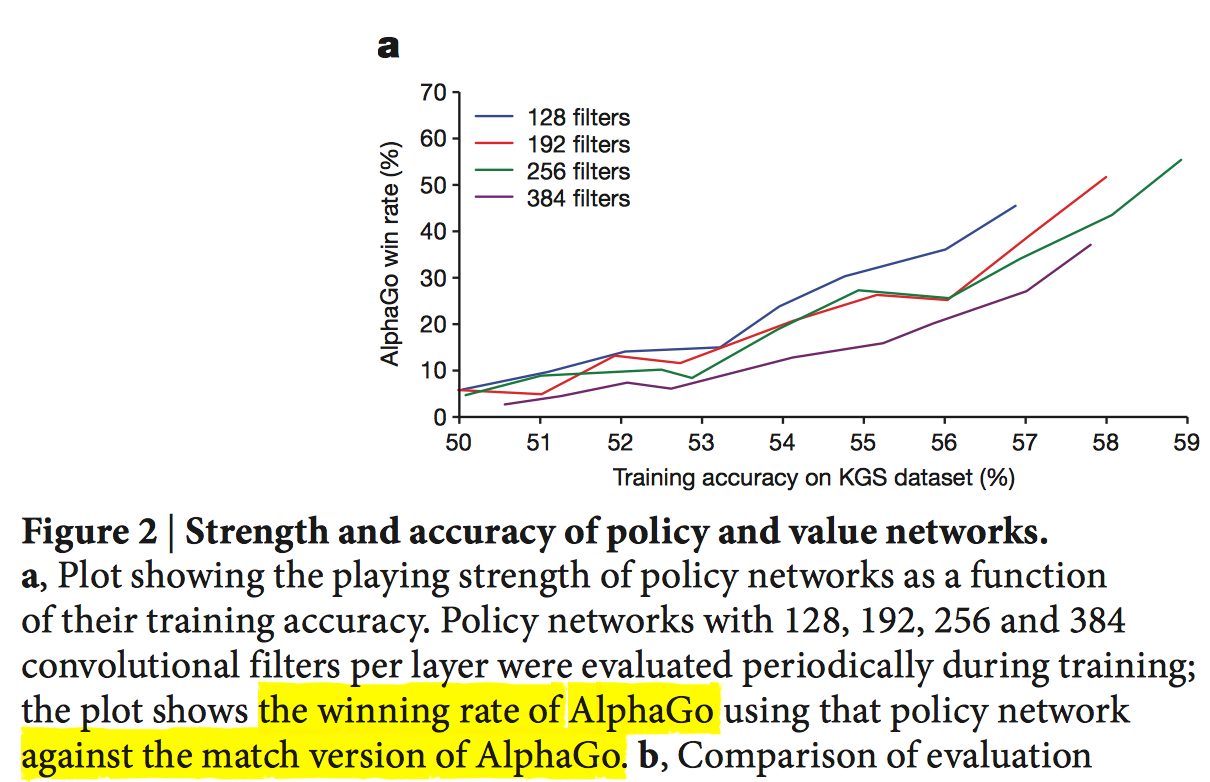
实际比赛：使用训练好的策略网络$P_\sigma$, 构造两个AlphaGo, 一方代表黑方，另一方代表白方，进行互相博弈，观察双方胜率情况。绘制出如下训练数据集大小和胜率关系曲线：

思考
1）两个AlphaGo都是使用相同的策略网络吗？ 
答： 如果两个AlphaGo相同，胜率应当是相当的。个人感觉更可能的是其中一个AlphaGo使用完整版的策略网
络是(100%数据集)，图中曲线绘制的是另一个随着训练集增加不断进化的AlphaGo的胜率，这样对比比较好。
这样，最终二者的胜率应当是相当的。按照这个理解的话，可以看到图中使用384层卷积网络的100%数据集的
AlphaGo更难被图中绘制对应的AlphaGo战胜，训练数据接近58%时，胜率才35%左右，也就说明越深的网络能
力更强。

快速走子策略$P_\pi$

目的：提高监督学习策略网络在搜索过程中的评估速度。
改进点：使用linear softmax和small pattern features，和$P_\sigma$对比的话，也就是将非线性改成线性，使用小的局部模式特征替换。
优化结果：准确率降低到24.2%，但是只需要2μs来选择下一步动作，相比前面$P_\sigma$需要3ms选择下一步动作。
用处：快速走子策略（Rollout Policy）可以用于下述蒙特卡罗搜索树搜索过程。

1 2	思考： 1）这里的small pattern features怎么翻译？是局部特征还是全局特征？

强化学习策略网络$P_\rho$

网络结构：和$P_\sigma$一致，权重$\rho$使用$P_\sigma$训练结果$\sigma$初始化，即：$\rho = \sigma $。在此基础上进行训练。
自我对弈（训练过程）：随机选择前面某个迭代周期得到的监督学习策略网络$P_\sigma$，然后使用当前的强化学习策略网络$P_\rho$和其对弈，目标是战胜先前的监督学习策略网络$P_\sigma$。随机的从一系列不同迭代周期的监督学习策略网络$P_\sigma$中选择对手是为了防止过拟合。
优化目标：战胜监督学习策略网络$P_\sigma$，但是实际上学习到的仍然是概率分布$P(a|s)$。使用Policy Gradient强化学习训练算法，将最终胜负报酬情况纳入考察，目标是最大化期望报酬，参考Deep Reinforcement Learning: Pong from Pixels。其主要原则是：如果某个动作能导致最终大的报酬，那么我们要尽可能增大该动作出现的概率，如果某个动作导致最终小的报酬，那么我们要尽可能减小该动作出现的概率。背后的原则是报酬驱动的。设计报酬函数$r(s)$, 非决胜步$r(s_t)=0$。决胜步若获胜则$z_t=r(s_T)=1$，说明该动作选择恰当，因此最大化该动作的对数似然值$log P_\rho(a_t|s_t) $; 若失败则$z_t=r(s_T)=-1$，说明该动作选择不好，此时最小化该动作的对数似然值$log P_\rho(a_t|s_t) $。统一起来，也就是最大化下述$\ell(\rho)$目标函数。随机梯度下降更新参数：
$$
\ell(\rho)= \sum log P_\rho(a_t|s_t) z_t \\
\Delta_\rho \propto \frac{\partial log P_\rho(a_t|s_t)}{\partial \rho}z_t
$$
上述目标函数等价于报酬期望最大化。推导如下：（见Deep Reinforcement Learning: Pong from Pixels），其中$f(x)$是更一般的报酬函数(例如,指数衰变报酬函数$R_t = \sum_{k=0}^{\infty} \gamma^k r_{t+k}$，AlphaGo中使用的是$±1$报酬函数），$p(x)$是策略网络学习到的策略分布。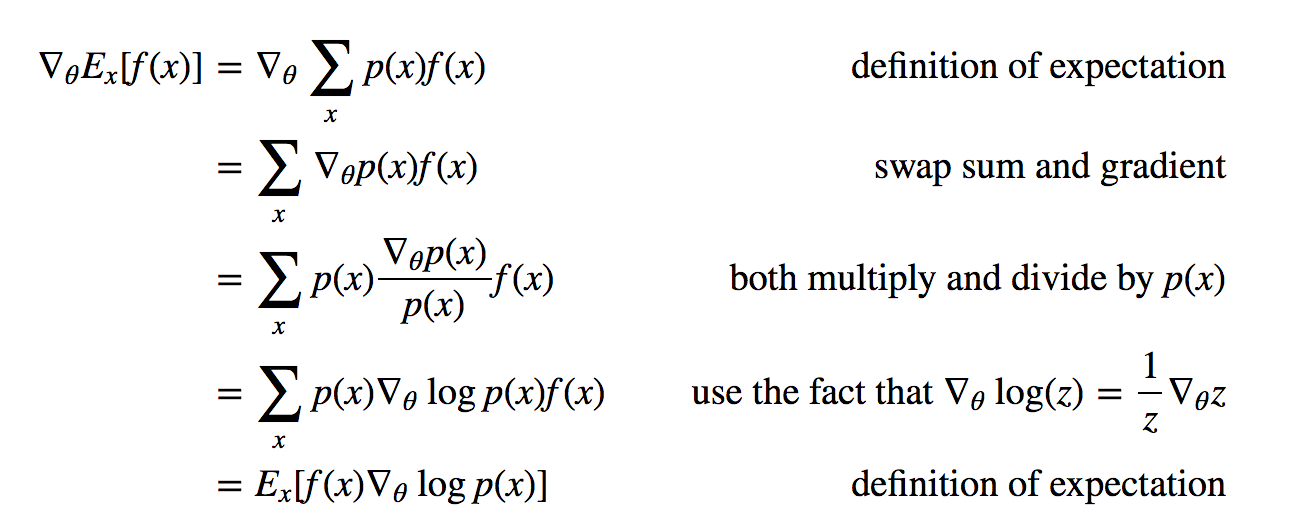

另外，这里的优化时间点我是这么理解的，每一局对应一轮优化。在每局中有很多时间步$t$, 每个时间步对应一个$t$时刻的棋面$s_t$，不断使用前一轮的强化学习策略网络进行自我对弈，一直到时间步$T$决出了该局的胜负报酬$r(s_T)$。此时进行神经网络参数更新，也就是回过头将该胜负标签$r(s_T)$贴到该局前面每个时间步对应的棋面$s_t$的标签上，构成一个数据对$(s_t, z_t)$, 至于$z_t=+r(s_T) or = -r(s_T)$，根据每个棋面$s_t$对应的下一步下棋方是$P_\rho$还是$P_\sigma$来确定。最后使用随机梯度下降对这些数据对$(s_t, z_t)$进行优化。
实战评估：使用强化学习策略网络$RL P_\rho$ PK 监督学习策略网络$SL P_\sigma$, 对于每个时刻的棋面，强化学习策略网络$P_\rho$得到在下一个时刻所有可选动作上的概率分布，强化学习策略网络根据该概率分布随机采样动作，作为下一步实际走子动作选择。最终强化学习策略网络$P_\rho$ 赢了80%的比赛。文中同时还测试了和当前最先进的，使用复杂的蒙特卡罗搜索树实现的围棋程序比赛Pachi（KGS业余组第二名），$RL P_\rho$ 最终赢了85%的比赛，而$SL P_\sigma$只赢了11%的比赛。

思考
1) 到目前为止，还没有使用蒙特卡罗搜索树，而是直接使用策略网络学习下一步如何走子，避免了向前看方式。
那为什么还要使用蒙特卡罗搜索树呢？
答：后续我们会发现只使用强化学习策略网络的AlphaGo只能战胜部分围棋程序，更不可能战胜人类顶尖职业选
手；后续会使用蒙特卡罗搜索树结合深度网络大幅度提升性能。其中深度网络能够大幅度提升蒙特卡罗搜索的效
率，而蒙特卡罗搜索树向前看搜索，能弥补策略网络只凭借当前棋面判断的劣势。

2）上述更新策略，简单的加上了梯度优化方向，且在决胜步出现后才能更新，能否进行优化？例如优化项是否可
以考虑获胜概率，概率大的加大更新幅度，小的减小更新幅度，来加快收敛；能否提前优化，例如在决胜步出现
前就进行优化？

3）强化学习的过程中，实际上可以生成新的数据集。

4）增强学习为何能够大幅提升能力呢？如果把监督学习网络比作小孩，那么增强学习网络就相当于职业选手了。
那么问题来了，2个6岁的小孩不断对弈，其水平就能达到职业选手的水平吗？

5) 强化学习策略网络的训练时使用Q-learning还是Policy Gradient?
文章中是说Policy Gradient Algorithm来训练强化学习策略网络，而不是Q-learning。
这两种算法有什么差别？

总结起来:
Q-learning: Value Based RL Algorithm。直接优化的是价值最大化，选择使价值最大的动作。
是一种通过价值间接学习策略的方法。
Policy Gradient: Policy Based RL Algorithm。直接学习策略分布，使用Policy Network
对策略函数进行逼近。基本思想是：如果某一个动作得到reward多，那么我们就使其出现的概率增大，如果某一
个动作得到的reward少，那么我们就使其出现的概率减小。reward也就是上述公式中的z_t。其背后主要原理
是将动作出现的概率和最终的报酬挂钩，且首要原则是最大化报酬，来调整动作出现的概率。

另外，Q-learning思想的实现代表是DQN，使用深度网络来进行函数逼近。
Deep Q learning: 通过调研，我发现DQN和正常的神经网络训练的的主要区别在于DQN要克服经验数据的
相关性（correlated data）和非平稳分布（non-stationary distribution)问题，（可以联想不同
棋谱之间的强相关性问题。）
代表性的解决方法包括NIPS 2013论文《Playing Atari with Deep Reinforcement 
Learning》提到的experience replay；Nature 2015论文《Human-level control through 
deep reinforcement learning》提到的iterative update以及AAAI 2016论文《Deep 
Reinforcement Learning with Double Q-learning》提到的Double Q-learning分离出两个Q网络。

强化学习价值网络$v_\theta$

目标：判断某个棋面s和策略P条件下，黑白棋双方最终赢棋可能性的相对值。注意，此时考察了胜负标签。
$$
v^p(s)=E[z_t|s_t=s, a_t…T \sim P]
$$
The final stage of the training pipeline focuses on position evaluation, estimating a value function $v^p (s)$ that predicts the outcome from position s of games played by using policy p for both players。
理论分析：理论上，我们希望估计在最优的策略$P^*$下的值函数（判断某个棋面s对于黑白棋双方赢棋的可能性）。实际上很难得到最优策略，我们使用强化学习策略网络$P_\rho$来近似最优策略$P^*$，并使用价值网络$v_\theta$来近似值函数。$v_\theta(s) \approx v^{P_\rho}(s) \approx v^*(s)$。
网络结构：和策略网络结构类似，但是输出的是某个棋面下，双方最终赢棋可能性的单一预测值。对比前面策略网络，输出的是某个棋面下，下一步所有走棋动作上的概率分布，用于下一步走棋。
训练学习：使用（棋面,最终输赢） $(state,outcome) pairs (s,z)$进行回归训练。优化目标是最小化平均均方误差MSE：

$$
min \frac{1}{2}(z-v_\theta(s))^2 \\
\Delta_\theta \propto \frac{\partial v_\theta(s)}{\partial \theta} (z-v_\theta(s))
$$

注意上述省略了负号，相应的更新也改成$+\Delta_\theta$

难点：直接从人类完整棋局中学习价值网络会导致过拟合。因为不同的棋面之间存在很强的相关性，有的甚至只有一个落子不同，导致价值网络学习时直接记住最后的输赢，而不能泛化到新的棋局。实际过程中训练集的损失为0.19，而测试集损失为0.37，相差比较大。
解决途径：使用RL强化学习策略网络进行自我对弈，生成3000万个棋面数据，每个棋面都是从单独的一局完整棋局中抽样出来的，相当于下了3000万局，每局抽1个棋面数据，共抽出3000万个棋面，这样能有效克服棋面之间的强相关性。使用该数据集最终得到0.226的训练集损失和0.234的测试集损失，有效得降低了过拟合。
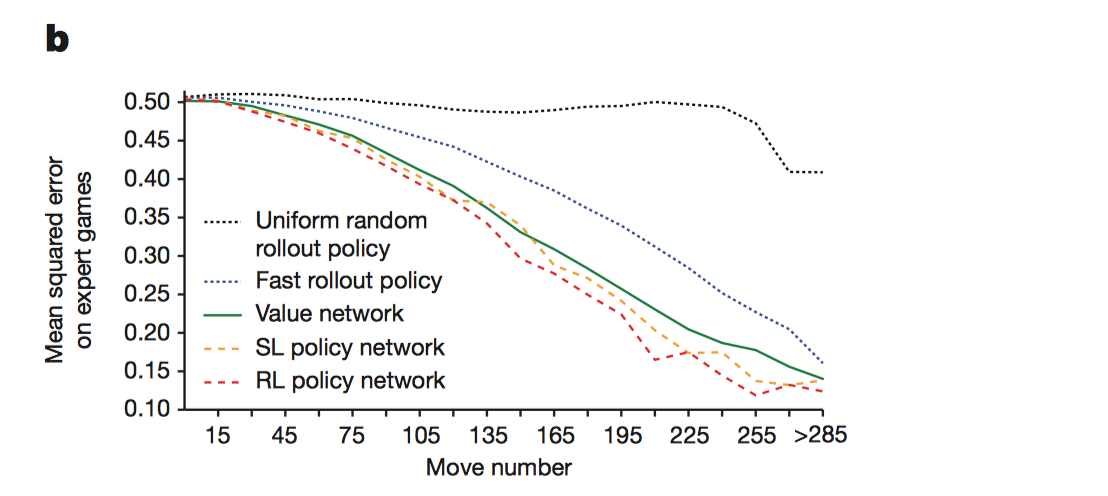
实验结果：对比值网络和使用不同策略的蒙特卡罗搜索树的实验结果。实验数据是人类棋局抽样出来的棋面，横轴代表棋面已经走的棋子数。对于某个棋面，计算其输赢的预测值和实际该棋面输赢情况的均方根误差。其中，值网络直接输入棋面，前向传播得到该棋面的输赢预测值。蒙特卡罗搜索树使用不同的策略，如监督学习策略网络、强化学习策略网络、正态随机走棋策略、快速走棋策略，模拟了从当前棋面开始的完整棋局，一直到分出胜负，共模拟100局，将100轮最终胜负相对值进行平均作为输赢预测值。值网络损失值随着棋面棋子的增多较平稳的下降。

思考
1）值网络训练时的标签z是如何设定的？
第一种理解是绝对的站在黑白双方角度。例如对于所有棋局黑方获胜z=1, 白方获胜z=-1。另一种理解是相对的
站在黑白双方角度，换句话说站在棋面角度，棋面确定了，接下来下棋的是黑方还是白方也相继确定了，因此判
断的是某个棋面下，接下来下棋的那方输赢的可能性。这样标注数据的时候，站在当前棋面的视角,该棋面接下来
下棋的那方输还是赢，如赢为1，输为-1。
此处是后者。stand in the perspective of the current player.

2）使用强化学习策略网络生成的棋面数据进行训练，这必须保证强化策略网络生成的数据是合理的、多样化的。
人类的比赛数据可能更倾向于局部最优解，囿于人类总结的各种围棋领域的先验知识；而强化策略网络生成的数
据更倾向于全局最优解，能够保证合理性和多样化。当然这个前提是，强化策略网络足够完美，能够媲美人类，
以至于生成的棋谱是优秀的。目前来看强化策略网络只能以85%的几率打败KGS上业余组第二的Pachi，实际上还
没有专业选手的实力。值网络的使用，加上后续和蒙特卡罗搜索树的结合，使得AlphaGo能够更上一层楼。

3）我们可以看到不管是策略网络还是值网络，其核心思想是利用深度网络来进行函数逼近。策略网络用于逼近策
略函数，值网络用于逼近值函数。传统的方法，策略函数和值网络的逼近只能采取简单的输入特征的线性组合进
行回归逼近，而深度学习能够利用更多的信息、更有效的进行函数逼近。

4) 值网络的训练还是很有意思的。使用无监督学习的强化学习生成训练数据后，再使用值网络进行有监督的学习。

在线使用MCTS组装深度网络

目前，上述提到的策略网络和值网络都已经离线训练好了。真正线上比赛的时候，使用MCTS蒙特卡罗搜索树将这些组件组装起来。归根结底，深度网络和MCTS结合是相得益彰的，深度网络能够大幅度提升蒙特卡罗搜索树搜索的效率，具体而言，策略网络减小搜索的宽度，值网络减小搜索的深度，而蒙特卡罗搜索树向前看的方式能够弥补深度网络只依赖于当前棋面判断局势的劣势。

蒙特卡罗搜索树核心要素

蒙特卡罗搜索树使用向前看搜索来选择下一步动作。树的核心要素包括：

节点：棋面s。每次轮到AlphaGo执棋时，都从当前棋面作为根节点开始进行搜索；模拟下完一步棋之后，得到另一个棋面，又从该棋面出发进行下一步模拟搜索。一直不断模拟搜索下去。
边：$(s, a)$, 从棋面s出发的下一步动作，每条边保存了该动作的效益值$Q(s,a)$, 访问次数$N(s,a)$, 和先验概率$P(s,a)$。

蒙特卡罗搜索树模拟过程

蒙特卡罗模拟搜索过程如下4阶段：

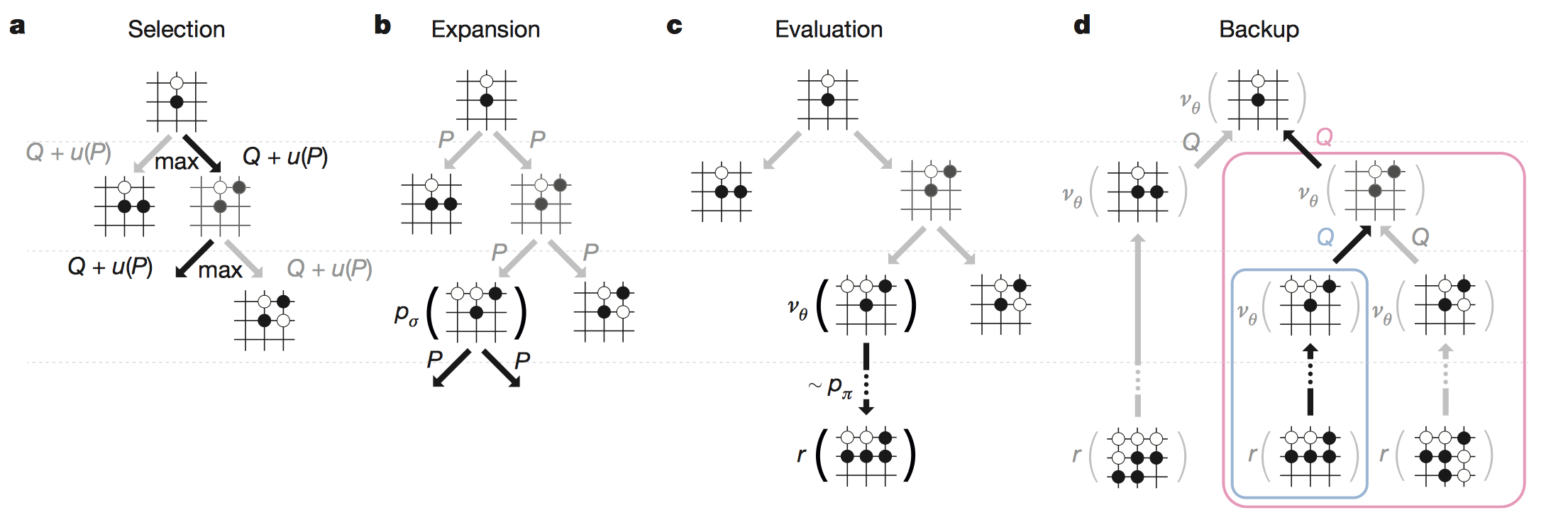
Selection：从根节点出发，在模拟过程的每个时刻$t$，选择该时刻的棋面$s_t$下的最佳动作$a_t$。

$$
a_t = \mathop{argmax}_{a}\left(Q(s_t, a) + u(s_t, a)\right) \\
u(s, a) \propto \frac{P(s,a)}{1+N(s, a)}
$$

即最大化动作效益值Q加上奖励u。其中奖励正比于先验概率，同时惩罚访问次数，鼓励其他探索，防止不同模拟老是走同一条路径。

Expansion: 当L时刻遍历到叶子节点$s_L$，且该叶子节点访问次数超过一定的阈值时，需要进行扩展。该叶子节点$s_L$对应的棋面使用监督学习策略网络$P_\sigma$处理且只处理1次，将$P_\sigma$的输出作为先验概率存放在每一个合法的动作边上，$P(s,a)=P_\sigma(a|s)$。
Evaluation: 对上述的叶子节点$s_L$进行胜率评估，判断当前棋面局势。使用两种途径进行评估。一种是直接使用值网络$v_\theta$预测胜率，得到$v_\theta(s_L)$；另一种是使用快速走子策略$P_\pi$，从被判断的位置出发，快速行棋至最后，每一次行棋结束后都会有个输赢结果，进行多轮行棋，然后综合统计得出该策略网络预测的胜率$z_L$。$v_\theta(s_L)，z_L$二者使用下述公式综合起来，得到该叶子节点的胜率评估值$V(s_L)$。
$$
V(s_L)=(1-\lambda)v_\theta(s_L) +\lambda z_L
$$
Backup: 上述对叶子节点评估完，代表着1次模拟结束。此时反向更新在此次模拟过程中到达上述叶子节点所经过的边的动作效益值$Q$以及访问次数$N$。n次模拟后，每条边累积的Q值更新量和访问次数更新量如下：
$$
N(s,a) = \sum_{i=1}^n I(s,a, i) \\
Q(s,a) = \frac{1}{N(s,a)} \sum_{i=1}^n I(s,a,i)V(s_L^i) \\
其中，I(s,a,i)代表第i次模拟是否经过该边(s,a) \\
s_L^i代表第i次模拟到达的叶子节点为s_L
$$

当所有n次模拟搜索都结束后，算法从根节点（当前棋面）选择访问次数最多的边对应的动作作为最终决策。

思考
1） 值得注意的是上述扩展阶段使用的是SL监督学习策略网络，而不是RL强化学习策略网络。也就是说模仿人类
走棋的SL结果更适合MCTS搜索，因为人类选择的是a diverse beam of promising 
moves，即考虑的是后续一系列步，这点跟MCTS本质较像；而RL学的是当前步的最优下法（whereas RL 
optimizes for the single best move）。不过另一方面，基于RL的value 
network比基于SL的value network评估方面效果更好。因此各有所长。

2） 最终决策是从根节点选择多次模拟过程中访问次数最多的边对应的动作作为最终决策，为什么不使用最大的Q
+u值的边对应的动作作为最终决策？这二者是否等价？还是说是经过实验评估才决定采取第一种策略？
At the end of search AlphaGo selects the action with maximum visit count; this 
is less sensitive to outliers than maximizing action value。

3） 还有个点要注意，蒙特卡罗搜索树实际上是复用的。前一个棋面搜索完进行决策走棋之后，对手走棋完，再
次轮到自己走棋的时候，复用上一次的蒙特卡罗搜索树，只不过做了些改进。一者，上次决策走棋对应的子节点
成为了根节点；二者，该子节点的子树被保留，包括子树上的信心、数据都保留；三者，其余部分全部舍弃。

4) AlphaGo在对手走棋的过程中，充分利用这部分时间，不断进行搜索，判断。

运行环境

策略网络和值网络的评估比传统的启发式搜索需要更大量级的计算。为了更有效的将MCTS和深度神经网络结合，AlphaGo使用异步多线程进行搜索，其中使用CPU执行模拟过程，使用GPU进行策略网络和值网络的并行计算。最终单机器版本的AlphaGo使用40个搜索线程，48个CPUs, 8GPUs。

同时还实现了分布式版本的AlphaGo, 使用多台机器，40个搜索线程，1202个CPUs，176个GPUs。分布式版本的AlphaGo运算速度更快，能够进行更复杂的搜索。

对比实验

考察AlphaGo和其他围棋程序的能力

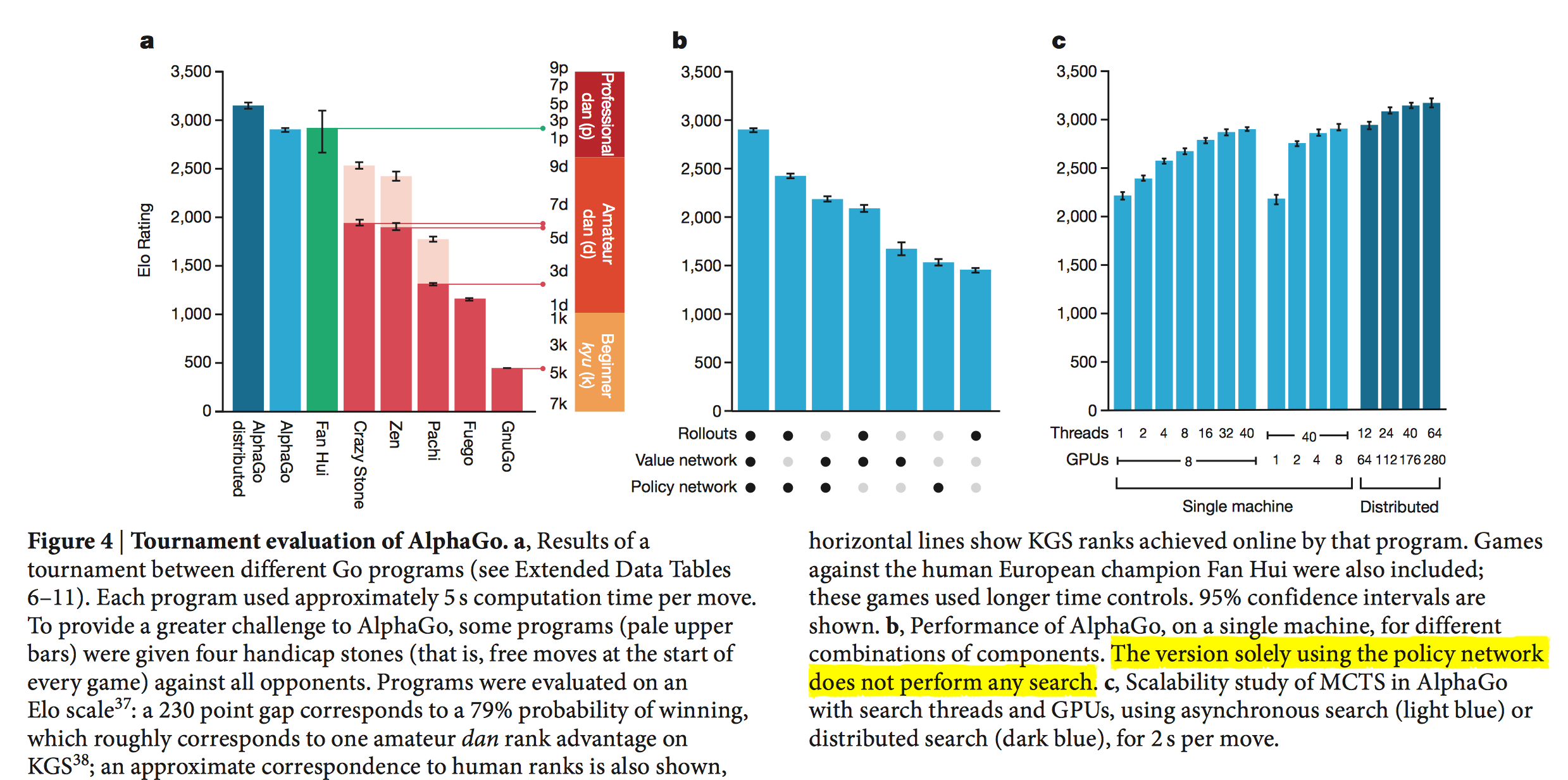
AlphaGo和目前主流的开源围棋程序以及欧洲围棋冠军樊麾进行比赛。单机器的AlphaGo和其他围棋程序的比赛中，AlphaGo赢了495场比赛中的494场，99.8%的胜率。为了加大难度，AlphaGo让4步，AlphaGo分别以77%，86%和99%的胜率战胜Crazy Stone, Zen和Pachi。而分布式的AlphaGo以77%胜率战胜单机器的AlphaGo，以100%胜率战胜其他所有的围棋程序。最后，单机器的AlphaGo能力几乎和欧洲围棋冠军樊麾相当，而分布式的AlphaGo能力已经大幅度超越樊麾。下图中显示的是KGS上的排名。下面还会进一步画出和樊麾的比赛示意图。

考察AlphaGo不同版本的能力

考察使用不同组件组成的AlphaGo的能力。完整版AlphaGo包括快速走子$P_\pi$、值网络$V_\theta$和SL策略网络$P_\sigma$。对比完整版AlphaGo、只使用其中两个组件的AlphaGo、只使用其中1个组件的AlphaGo的能力。其中只使用策略网络的AlphaGo不使用蒙特卡罗搜索，其余都是结合了蒙特卡罗搜索。只使用值网络，意味着上述蒙特卡罗评估阶段$\lambda=0$；只使用快速走子，则$\lambda=1$。观察到，使用值网络和策略网络的AlphaGo战胜了所有的围棋程序。

1
2
3

思考
1）这里的疑问是，上述蒙特卡罗扩展节点阶段是依赖于SL策略网络进行的，对于不使用策略网络版本的
AlphaGo，蒙特卡罗搜索过程的Expansion扩展阶段又是怎么进行的？

考察AlphaGo的扩展能力

考察随着CPU、线程数、GPU变化，单机器AlphaGo和分布式AlphaGo的能力值变化。
考察值网络和快速走子策略的组合参数$\lambda$

实验表明$\lambda=0.5$时，性能最优。这说明值网络（Value Network）和快速走子策略(Fast Rollout Policy)实际上可以互补。值网络考察到目前为止的形势判断，快速rollout模拟到终局的形势判断，二者综合起来性能更优。
考察单机器AlphaGo和人类顶尖高手对决

下图是不同版本AlphaGo同时和FanHui比赛的某个时刻的棋面。
- a: 值网络：枚举下一步动作，将下一步动作之后的棋面输入值网络，得到该棋面的获胜概率。选择最大赢棋概率的那一步走。这个计算量还是很大的，需要估计棋盘所有的位置，图中蓝色部分都是要考察的情况。
- b: 蒙特卡罗搜索+值网络：选择根节点出发的边中Q值最大的动作作为最终决策。
- c:蒙特卡罗搜索+快速Rollouts: 选择根节点出发的边中Q值最大的动作作为最终决策。
- d: 监督学习策略网络$P_\sigma$：选择似然可能性$p_\sigma(a|s)$最大的下一步动作, 图中只显示似然值大于0.1%的走法。
- e: 蒙特卡罗搜索+监督学习策略网络+值网络+快速Rollouts: 选择根节点出发所有模拟过程访问次数最多的边所对应的动作。
- f: 主变化，AlphaGo预测多步，包括黑棋最佳下法，白棋最佳下法。AlphaGo走完这一步后，FanHui白棋实际下法是图中白色正方形，而AlphaGo预测的白棋最佳下法是图中白色圆圈1。赛后FanHui评价说更倾向于AlphaGo的下法，而不是自己实际的下法。可见AlphaGo的强大之处。

考察分布式AlphaGo和人类顶尖高手对决

下图是分布式AlphaGo和FanHui进行的5局对决的终局棋面。分布式AlphaGo以5:0战胜FanHui。

总结

AlphaGo总体上包含离线学习和在线对弈两个过程。

离线学习包括三个阶段。

第一阶段：训练监督学习策略网络。

利用3000万多幅职业棋手对局的棋谱来训练两个监督学习策略。
- 一个是基于全局特征和深度卷积网络(CNN)训练出来的策略网络$P_\sigma$(Policy Network)，其主要作用是给定当前棋面状态作为输入，输出下一步棋在棋盘其它空地上的落子概率。
- 另一个是利用局部特征和线性神经网络模型训练出来的快速走子策略(Fast Rollout Policy)。
策略网络速度较慢，但精度较高；快速走子策略反之。-
第二阶段：训练强化学习策略网络。

利用先前训练好的监督学习策略网络初始化强化学习策略网络，然后随机挑选前面第t轮的策略网络和该强化学习网络互相对弈，利用增强式学习来修正强化学习策略网络的参数，最终得到增强的策略网络。
第三阶段：训练值网络。

利用增强学习策略网络自我对弈生成3000万个棋谱以及对应的输赢情况(实际过程如下图所示，每局先用监督学习策略网络生成U步，接着再使用强化学习策略网络自我对弈到决出胜负)，每个棋谱随机抽样1个棋面数据，构成3000万个棋面和实际输赢情况标签的训练数据，使用值网络进行回归训练，目标是最小化输赢预测的均方根误差损失。

在线对弈包括6个关键点，核心思想是在蒙特卡罗搜索树中嵌入深度神经网络来减小搜索空间。策略网络能够减小搜索的宽度，在扩展阶段发挥作用；值网络能够减小搜索的深度，在评估阶段发挥作用。

关键点$1$：根据当前棋面提取相应特征。
关键点$2 \sim 5$：蒙特卡罗搜索模拟4阶段。
- $Selection$阶段：选择下一步动作，进行棋面状态转移。$a_t=argmax_{a}\left(Q(s_t, a) + u(s_t, a)\right)$
- $Expansion$阶段：遇到叶子节点且该叶子节点访问次数超过给定的阈值时则进行扩展。使用监督学习策略网络估计该叶节点对应的棋面下，下一步走法其他动作的概率$p(a|s)$，作为先验概率存放在对应的动作边上。
- $Evaluation$阶段：使用价值网络和快速走子策略对叶子节点进行局势判断。每次模拟走到叶子节点时，对叶子节点进行评估。使用价值网络和快速走子策略预测该叶子节点对应的棋面赢棋的可能性。其中值网络直接输入棋面特征，预测赢棋的可能性大小；快速走子策略进行多轮rollouts模拟，每轮rollouts从该叶子节点对应的棋面出发走棋，一直到决出胜负，平均多轮胜负情况作为赢棋可能性的预测值。
- $Backup$阶段：更新$Q$值和访问次数$N$值。上述评估阶段完成后，代表此次模拟结束，此时进行反向传播更新此次模拟到达该叶子节点所经过的所有边上的$Q$值和访问次数$N$。更新完的$Q$值和$N$值用于下一轮模拟，下一轮模拟$Selection$阶段会使用新的$Q$值和$N$值选择下一步动作进行状态转移。
关键点6：所有轮次的模拟结束后，选择和根节点（当前棋面）相连接的、访问次数最多的边所对应的动作，作为下一步棋的走法。

下图是从网上找到的一个较好的AlphaGo原理总结图。

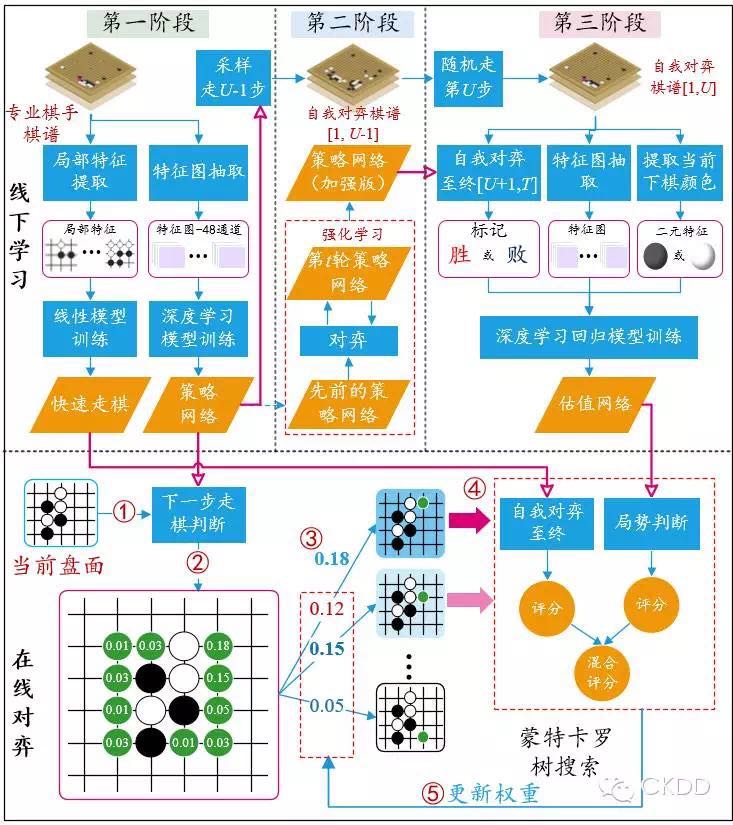
展望思考

阅读完论文，个人感觉这篇论文的核心仍然在于蒙特卡罗搜索树，本质上仍然和传统的方法一致。传统的蒙特卡罗搜索树致力于搜索空间的减小，原则包括减小搜索宽度和减小搜索深度。而本文的出彩点只不过是应用深度网络的方法来有效减少蒙特卡罗搜索空间。也是从两个原则出发，其中策略网络在蒙特卡罗树扩展阶段减小搜索的宽度，而值网络在蒙特卡罗树评估阶段减小搜索的深度。进一步，这两个原则的核心思想是利用深度网络来进行函数逼近。策略网络用于逼近策略函数，价值网络用于逼近价值函数。传统的方法，策略函数和价值网络的逼近只能采取简单的输入特征的线性组合进行回归逼近，而深度学习能够利用更多的信息、更有效的进行函数逼近。实际上，这里的深度学习解决了传统的树搜索过程中启发式评分函数问题。当然，这篇论文出彩点也包括深度学习和强化学习的结合实践，但是这也是为蒙特卡罗搜索树搜索效率服务的。整体而言，仍然脱离不了蒙特卡罗搜索树。

未来可能的工作，一种是继续优化蒙特卡罗搜索树，引入不同的方法将蒙特卡罗4个阶段继续做精做细，比如尝试使用其他的深度学习模型，尝试优化强化学习算法，尝试引入新的AI组件或改变、重组现有的AI组件等。另一种是发展不依赖于蒙特卡罗搜索树的新算法，主要原因是蒙特卡罗搜索树并非完美，其本质仍然是穷举搜索，只不过是更智能的搜索，对于一些复杂的围棋套路“对杀、打劫和关子”等，不能有效的减小搜索空间，使得计算量较大，甚至出现错误，调研发现南京大学的周志华教授曾经撰文指出过打劫会让AlphaGo价值网络崩溃的问题。这方面研究包括AAAI 2017论文“Beyond Monte Carlo Tree Search: Playing Go with Deep Alternative Neural Network and Long-Term Evaluation”，文中提到了使用深度交替神经网络DANN和长期评估LTE来代替蒙特卡罗搜索，这篇文章结尾还提到来自计算机视觉领域的残差网络也有可能帮助 DANN 获得性能提升，巧的是这篇文章是在AlphaGo Zero论文发布前发表的，而AlphaGo Zero恰恰使用了残差网络。

后续我会继续研究AlphaGo Zero以及AlphaZero的论文。