蘑菇先生学习记

推荐系统算法调研

发表于 | 分类于 | 阅读量

本文对目前流行的推荐系统算法进行调研，主要参考三篇综述和一本手册。综述包括：推荐系统主流算法综述、基于协同过滤技术的推荐系统算法综述、基于深度学习的推荐系统算法综述。手册是经典推荐系统参考手册。另外，还会不断跟进目前主流和前沿的推荐技术，本调研会不断更新。

欢迎关注我的公众号”蘑菇先生学习记”，更快更及时地获取推荐系统前沿进展！

qr

学科定义

  • 独立学科：1990’s 成立独立学科，契机在于研究者开始关注依赖于评分结构的推荐问题。推荐问题被约减为关于如何估计用户对未曾见过的商品进行评分的问题，这样就能推荐给用户这些商品中最高估计评分的商品。

  • 学科存在意义：随着当今技术的飞速发展，数据量也与日俱增，人们越来越感觉在海量数据面前束手无策。正是为了解决信息过载(Information overload)的问题，人们提出了推荐系统（与搜索引擎对应，人们习惯叫推荐系统为推荐引擎）。当我们提到推荐引擎的时候，经常联想到的技术也便是搜索引擎。

    二者有共同的目标，即解决信息过载问题，但具体的做法因人而异。

    搜索引擎更倾向于人们有明确的目的，可以将人们对于信息的寻求转换为精确的关键字，然后交给搜索引擎最后返回给用户一系列列表，用户可以对这些返回结果进行反馈，并且是对于用户有主动意识的，但它会有马太效应的问题，即会造成越流行的东西随着搜索过程的迭代会越流行，使得那些越不流行的东西石沉大海。

    而推荐引擎更倾向于人们没有明确的目的，或者说他们的目的是模糊的，通俗来讲，用户连自己都不知道他想要什么，这时候正是推荐引擎的用户之地，推荐系统通过用户的历史行为或者用户的兴趣偏好或者用户的人口统计学特征来送给推荐算法，然后推荐系统运用推荐算法来产生用户可能感兴趣的项目列表，同时用户对于搜索引擎是被动的。其中长尾理论（人们只关注曝光率高的项目，而忽略曝光率低的项目）可以很好的解释推荐系统的存在，试验表明位于长尾位置的曝光率低的项目产生的利润不低于只销售曝光率高的项目的利润。推荐系统正好可以给所有项目提供曝光的机会，以此来挖掘长尾项目的潜在利润。

    如果说搜索引擎体现着马太效应的话，那么长尾理论则阐述了推荐系统所发挥的价值。

  • 形式化定义：$C$：all users, $ S$: all items, $u$: utility function, 效用函数衡量商品对用户的有用程度。例如：$C \times S \rightarrow R$ ，$R$是有序集合。这样对于用于$c \in C$, 我们可以选择商品$s’ \in S$,来最大化效用函数。
    $$
    \forall c \in C, s_{c}’ = \mathop{argmax}_{s \in S} u (c,s)
    $$
    通常商品的效用会使用评分（rating）来代表。然而，实际上效用可以使用任意的函数，包括面向商业目标的Profit function。

    用户空间$C$中的每个元素对应该用户多种多样特征构成的用户画像，例如年龄、性别、收入、婚姻状况等。最简单的情况，用户画像仅包含User ID。同样，商品空间$S$的每个元素对应该商品的特征集合。例如对于电影推荐，特征集合包括该电影的ID，名称，类别，导演，发行年份，主演等。

  • 核心问题：推荐系统的核心问题在于效用$u$通常不定义于整个$C \times S$空间，而只是其中的一些子集。这意味着$u$必须被推断到整个$C \times S$空间。在推荐系统中，效用$u$通常在一开始被初始化为用户对商品的评分。然而存在很多商品，用户未曾评分过，故推荐系统的任务就是要估计用户对这些未曾评分的商品的评分情况。这种从已知到未知的推断过程通常使用特定的、能够定义效用的启发式打分方法实现，并经验性的验证性能；或者通过优化某个特定的性能指标（如MSE）来拟合效用函数。

算法分类

推荐系统算法大体有两种分类方法，一种是根据推荐的依据进行划分，另一种是根据推荐的最终输出形式进行划分。

根据推荐的依据分类

  • Content-based recommenders: 推荐和用户曾经喜欢的商品相似的商品。 主要是基于商品属性信息和用户画像信息的对比。核心问题是如何刻画商品属性和用户画像以及效用的度量。方法包括：

    • Heuristic-based method: 对于特征维度的构建，例如基于关键字提取的方法，使用TF-IDF等指标提取关键字作为特征。对于效用的度量，例如使用启发式cosine相似性指标，衡量商品特征和用户画像的相似性，似性越高，效用越大。
    • Machine learning-based mehod：对于特征维度的构建，使用机器学习算法来构建用户和商品的特征维度。例如建模商品属于某个类别的概率，得到商品的刻画属性。对于效用的度量，直接使用机器学习算法拟合效用函数。

  • Collaborative recommenders: 推荐和用户有相似品味和偏好的用户喜欢过的商品。主要是基于用户和商品历史交互行为信息，包括显示的和隐式的。协同过滤方法进一步细分为：

    • Memory-based CF: 基于内存的协同过滤方法。直接对User-Item矩阵进行研究。通过启发式的方法来进行推荐。核心要素包括相似性度量和推荐策略。相似性度量包括Pearson或Cosine等；而最简单的推荐方法是基于大多数的推荐策略。

      • User-based CF: 推荐给特定用户列表中还没有发生过行为、而在相似用户列表中产生过行为的高频商品。
      • Item-based CF: 推荐给特定用户列表中还没有发生过行为、并且和已经发生过行为的商品相似的商品。

    • Model-based CF: 基于模型的协同过滤方法。主要是运用机器学习的思想来进行推荐。主要包括：

      • 基于流形学习的矩阵降维/分解算法: SVD、FunkSVD、BiasSVD、SVD++、NMF等。
      • 基于表示学习的深度学习算法：MLP、CNN、AutoEncoder、RNN等。
      • 基于图/网络模型的算法：MDP-based CF、Bayesian Belief nets CF、CTR(协同主题回归，将概率矩阵分解和主题模型结合应用于推荐系统)等。
      • 其它：包括基于聚类的CF、稀疏因子分析CF、隐语义分析CF等等。

    • Hybrid CF: 结合多种方式的CF算法。如Content-based CF、Content-boosted CF或者结合Memory-based和Model-based CF混合方法。

      overview

      ​

      协同过滤算法分类

  • Hybrid approaches: 混合方法。综合集成上述两种方法。

    当前推荐算法主要是基于内容(CB)、协同过滤(CF)、混合算法。基于内容的推荐依靠用户profile和item的描述做推荐。CF基于过去的的表现和行为推荐。由于种种原因，收集过去的行为比收集用户画像要容易，但CF又有他的局限性，当打分（rating）很稀疏时，预测精度会下降很厉害，同时，新产品的冷启动也是CF的问题。因此，近年来，混合方法应用比较广。

    type

    ​

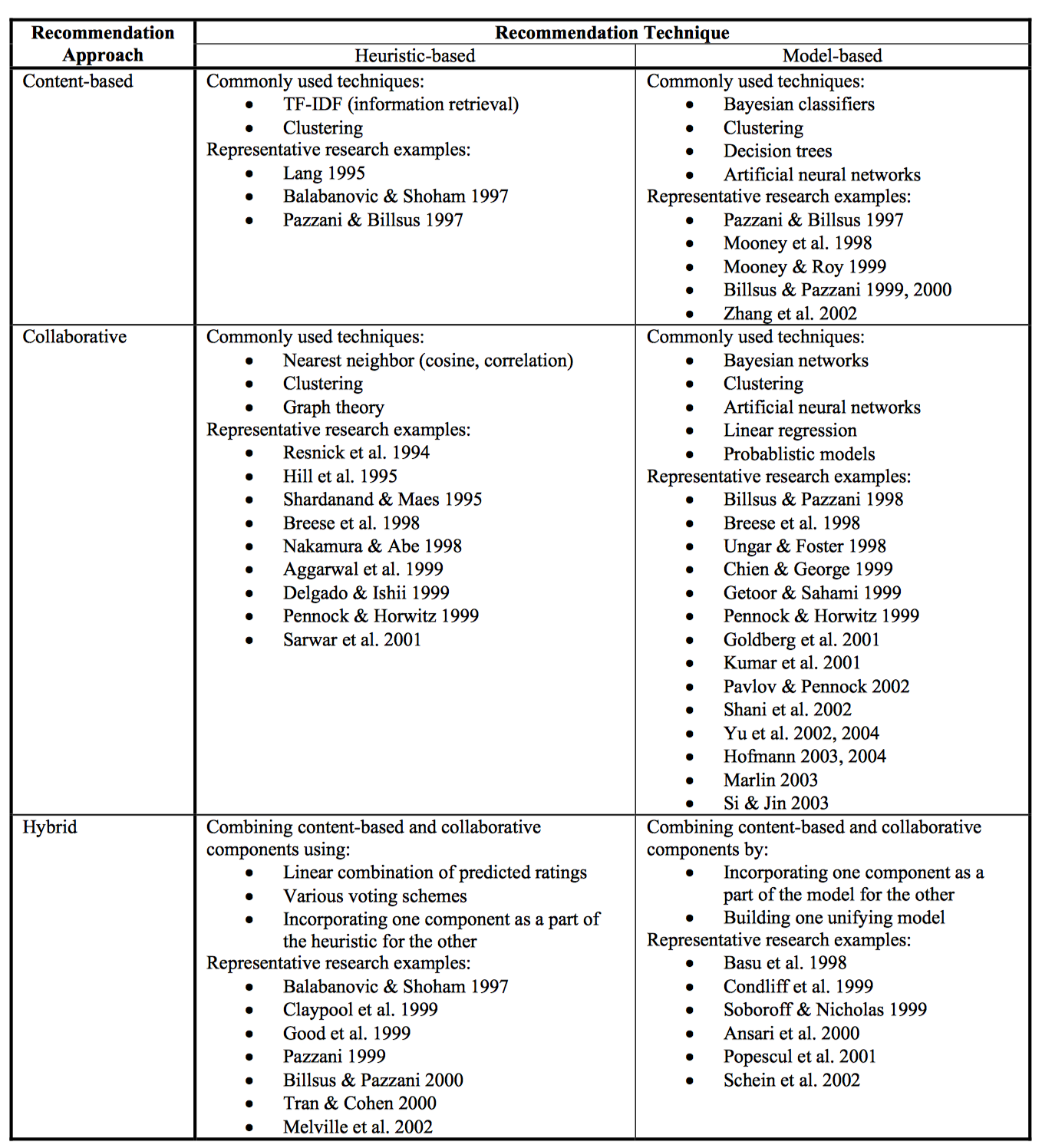
    推荐系统算法分类

除此以外，还有两种形式的推荐算法也很流行。

  • Constraint-based Recommenders: 基于约束的推荐。
  • Context-Aware Recommenders: 基于上下文信息的推荐。

根据推荐的最终输出形式分类

  • Rating prediction：评分预测模型，核心目的是填充用户-商品评分矩阵中的缺失值。
  • Ranking prediction (top-n recommendation) ：排序预测模型，核心目的是推荐一个有序的商品列表给用户。

  • Classification：分类模型，核心目的是把候选商品划分成正确的类别，并用于推荐。

    通常推荐最终输出形式决定了推荐系统的衡量指标，例如Rating prediction通常使用RMSE、MAE等，Ranking prediction通常使用Precision@K、Recall@K等，Classification通常使用Accuracy等。

基于启发式的邻域推荐算法

基于启发式的邻域推荐算法包括，User-based CF, Item-based CF, Slope-One等。这部分比较简单，简写。

User-based CF

核心思想：选择相似用户喜好的商品推荐给用户。
$$
\hat{r}_{ui} = \frac{
\sum\limits_{v \in N^k_i(u)} \text{sim}(u, v) \cdot r_{vi}}
{\sum\limits_{v \in N^k_i(u)} \text{sim}(u, v)}
$$
核心问题：如何度量用户相似性$sim(u,v)$, 可选方案包括cosine similarity、pearson correlation coefficient.

上述进一步改进，加入用户偏好，使用用户评分均值作为偏好。
$$
\hat{r}_{ui} = \mu_u + \frac{ \sum\limits_{v \in N^k_i(u)}
\text{sim}(u, v) \cdot (r_{vi} - \mu_v)} {\sum\limits_{v \in
N^k_i(u)} \text{sim}(u, v)}
$$
进一步改进，使用z-score。
$$
\hat{r}_{ui} = \mu_u + \sigma_u \frac{ \sum\limits_{v \in N^k_i(u)}
\text{sim}(u, v) \cdot (r_{vi} - \mu_v) / \sigma_v} {\sum\limits_{v
\in N^k_i(u)} \text{sim}(u, v)}
$$

Item-based CF

核心思想：选择和用户曾经评分较高商品的相似商品推荐给用户。

算法基本上和上述类似，只不过考察的是物品之间的相似性。
$$
\hat{r}_{ui} = \frac{
\sum\limits_{j \in N^k_u(i)} \text{sim}(i, j) \cdot r_{uj}}
{\sum\limits_{j \in N^k_u(j)} \text{sim}(i, j)} \\
\hat{r}_{ui} = \mu_i + \frac{ \sum\limits_{j \in N^k_u(i)}
\text{sim}(i, j) \cdot (r_{uj} - \mu_j)} {\sum\limits_{j \in
N^k_u(i)} \text{sim}(i, j)} \\
\hat{r}_{ui} = \mu_i + \sigma_i \frac{ \sum\limits_{j \in N^k_u(i)}
\text{sim}(i, j) \cdot (r_{uj} - \mu_j) / \sigma_j} {\sum\limits_{j
\in N^k_u(i)} \text{sim}(i, j)}
$$
同样有上述3种演进方法。

Slope-One

其基本的想法来自于简单的一元线性模型$w=f(v)=v+b$。已知一组训练点$(v_i,w_i)^n_{i=1}$，用此线性模型最小化预测误差的平方和，我们可以获得: $b=\frac{\sum_i (w_i-v_i)}{n}$。利用上式获得了$b$的取值后，对于新的数据点$v_{new}$，我们可以利用 $w_{new}=b+v_{new}$获得它的预测值。一个形象的例子如下：

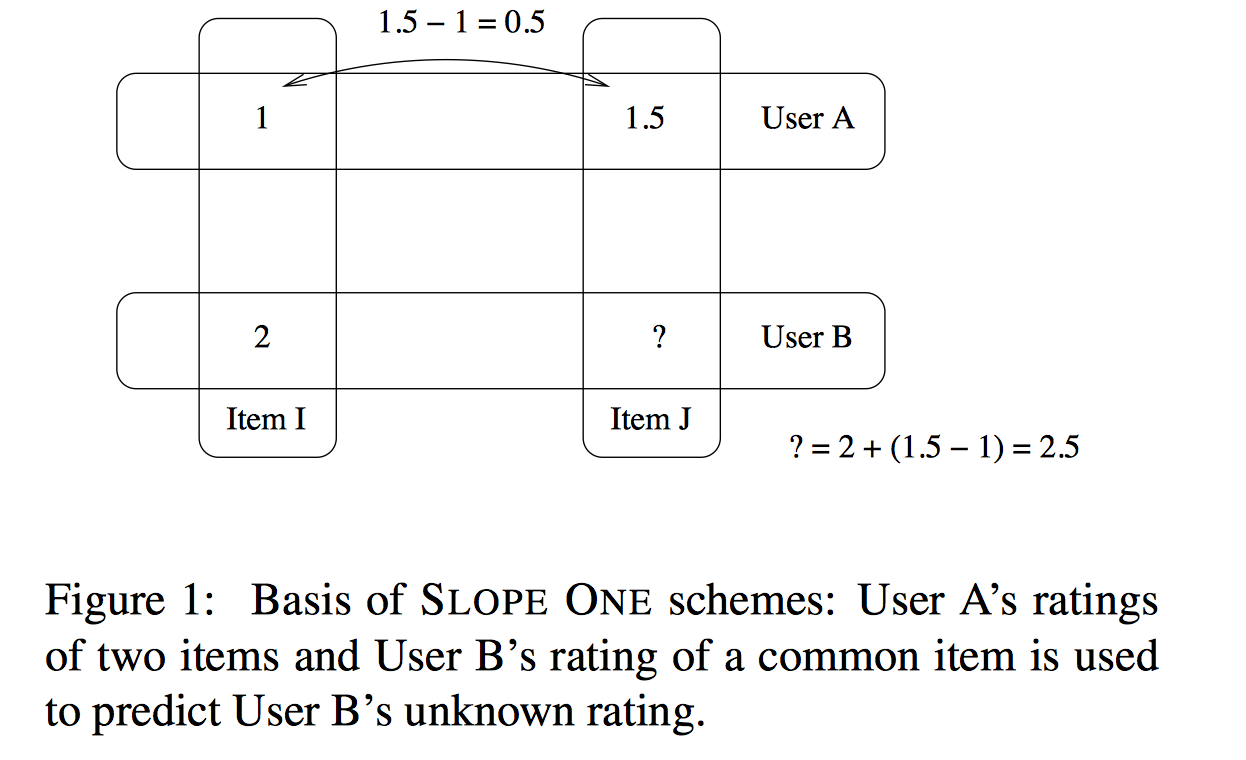
slope-one

直观上我们可以把上面求偏移$b$的公式理解为 $w_i$ 和 $v_i$差值的平均值。

概括来说，为了预测用户$u$对商品$i$的评分, 那么就使用$u$产生过行为的商品集合$R(u)$, 对每个商品$j \in N(u)$, 按照上述思想求差值，最后再取平均，得到$dev(i,j)$, 最终在所有的商品$j$上求得$dev(i,j)$, 再应用下述公式估计评分$\hat{r}_{u,i}$：
$$
dev(i, j) = \frac{1}{|U_{ij}|}\sum\limits_{u \in U_{ij}} r_{ui} - r_{uj} \\
\hat{r}_{ui} = \mu_u + \frac{1}{|R_i(u)|}\sum\limits_{j \in R_i(u)} dev(i, j)
$$

另外，还有一种加权的slope one算法。不同商品和$i$求差值时，可能共同评分的用户数量不同，使用用户数量进行加权：$U_{ij}$是对商品$i$和$j$同时评分的用户集合。
$$
dev(i, j) = \frac{1}{|U_{ij}|}\sum\limits_{u \in U_{ij}} r_{ui} - r_{uj} \\
\hat{r}_{ui} = \frac{\sum\limits_{j \in R_i(u)}(dev(i, j)+r_{u,j}) |U_{ij}|}{\sum\limits_{j \in R_i(u)} |U_{ij}|}
$$

Swing

基于图结构的实时推荐算法Swing，能够计算item-item之间的相似性。Swing指的是秋千，用户和物品的二部图中会存在很多这种秋千，例如$(u_1, u_2, i_1)$, 即用户1和2都购买过物品$i$，三者构成一个秋千(三角形缺一条边)。这实际上是3阶交互关系。传统的启发式近邻方法只关注用户和物品之间的二阶交互关系。Swing会关注这种3阶关系。这种方法的一个直觉来源于，如果多个user在点击了$i_1$的同时，都只共同点了某一个其他的$i_2$，那么$i_1$和$i_2$一定是强关联的，这种未知的强关联关系相当于是通过用户来传递的。另一方面，如果两个user pair对之间构成的swing结构越多，则每个结构越弱，在这个pair对上每个节点分到的权重越低。公式如下：
$$
Sim(i,j)=\sum_{u \in U_i \cap U_j} \sum_{v \in U_i \cap U_j} \frac{1}{\alpha+|I_u \cap I_v|}
$$
为了衡量物品$i$和$j$的相似性，考察都购买了物品$i$和$j$的用户$u$和$v$， 如果这两个用户共同购买的物品越少，则物品$i$和$j$的相似性越高。极端情况下，两个用户都购买了某个物品，且两个用户所有购买的物品中，共同购买的物品只有这两个，说明这两个用户兴趣差异非常大，然而却同时购买了这两个物品，则说明这两个物品相似性非常大！

基于矩阵分解的推荐算法

参考

Matrix factorization techniques for recommender systems

Probabilistic Matrix Factorization

首先明确所要解决的问题，即对于一个评分矩阵User-Item Matrix，这个矩阵是很稀疏的，用户对于商品的评分是不充分的，大部分是没有记录的，我们的任务是要通过分析已有的数据（观测数据）来对未知数据进行预测，即这是一个矩阵补全（填充）任务。矩阵填充任务可以通过矩阵分解技术来实现。核心思想是将用户和商品映射到一个共同的隐空间，使得在这个隐空间中，用户和商品的交互行为（如打分等）可以使用向量内积来建模。这一隐空间借助从评分矩阵自动推断得到的隐因子，来刻画用户和商品，以解释用户对商品的评分行为。

Traditional SVD

$$
R_{m\times n} = U_{m \times k} \Sigma_{k \times k} V_{k \times n}^T
$$

SVD分解的形式为3个矩阵相乘，中间矩阵为奇异值矩阵。如果想运用SVD分解的话，有一个前提是要求矩阵是稠密的，即矩阵里的元素要非空，否则就不能运用SVD分解。很显然我们的任务还不能用SVD，所以一般的做法是先用均值或者其他统计学方法来填充矩阵，然后再运用SVD分解降维。

FunkSVD

刚才提到的Traditional SVD首先需要填充矩阵，然后再进行分解降维，同时存在计算复杂度高和空间消耗大的问题。FunkSVD不再将矩阵分解为3个矩阵，而是分解为2个低秩的用户和商品矩阵。
$$
\hat{r}_{u,i} = q_i^T p_u
$$
$q_i$是商品$i$在隐空间的向量表示形式, 衡量了商品具有这些隐因子特性的程度；$p_u$是用户$u$在隐空间的向量表示，衡量了用户对这些隐因子的感兴趣程度。二者乘积衡量了用户对该商品的评分。

FunkSVD使用损失函数+梯度下降的方法进行学习：
$$
\mathop{min}_{q^*, p^*} \sum_{(u,i) \in R_{train}} (r_{u,i} - q_i^T p_u)^2 + \lambda (||q_i||^2 + ||p_u||^2 )
$$
$R_{train}$ 是评分矩阵中可观测的数据对构成的集合（即$r_{u,i}$未缺失的记录构成的集合）。

BiasSVD

在FunkSVD提出来之后，出现了很多变形版本，其中一个相对成功的方法是BiasSVD，顾名思义，即带有偏置项的SVD分解。它是基于这样的假设：用户存在个人偏好、商品天生具有贵贱之分。某些用户会自带一些特质，比如天生愿意给别人好评，而有的人就比较苛刻。同时也有一些这样的商品，一被生产便决定了它的地位，有的比较受人们欢迎，有的则被人嫌弃，这也正是提出用户和项目偏置项的原因。概括起来而言，对于一个评分系统有些固有属性和用户物品无关，而用户也有些属性和物品无关，物品也有些属性与用户无关。
$$
\hat{r}_{ui} = \mu + b_u + b_i + q_i^Tp_u \\
min \sum_{r_{ui} \in R_{train}} \left(r_{ui} - \hat{r}_{ui} \right)^2 +
\lambda\left(b_i^2 + b_u^2 + ||q_i||^2 + ||p_u||^2\right)
$$
使用梯度下降进行更新：其中$e_{ui} = r_{ui} - \hat{r}_{ui}$
$$
\begin{split}b_u &\leftarrow b_u &+ \gamma (e_{ui} - \lambda b_u)\\
b_i &\leftarrow b_i &+ \gamma (e_{ui} - \lambda b_i)\\
p_u &\leftarrow p_u &+ \gamma (e_{ui} \cdot q_i - \lambda p_u)\\
q_i &\leftarrow q_i &+ \gamma (e_{ui} \cdot p_u - \lambda q_i)\end{split}
$$

SVD++

后来又提出了对BiasSVD改进的SVD++。它是基于这样的假设：除了显示的评分行为以外，用户对于商品的浏览记录或购买记录（隐式反馈）也可以从侧面反映用户的偏好。相当于引入了额外的信息源，能够解决因显示评分行为较少导致的冷启动问题。其中一种主要信息源包括：用户$u$产生过行为(显示或隐式)的商品集合$N(u)$, 可以引入用户$u$对于这些商品的隐式偏好$y_j$
$$
\hat{r}_{ui} = \mu + b_u + b_i + q_i^T\left(p_u +
|N_u|^{-\frac{1}{2}} \sum_{j \in N_u}y_j\right) \\
min \sum_{r_{ui} \in R_{train}} \left(r_{ui} - \hat{r}_{ui} \right)^2 +
\lambda\left(b_i^2 + b_u^2 + ||q_i||^2 + ||p_u||^2 + \sum_{j \in N_u} ||y_j||^2 \right)
$$
其中$N(u)$为用户$u$所产生行为的物品集合；$y_j$为隐藏的、对于商品$j$的个人喜好偏置（相当于每种产生行为的商品都有一个偏好$y_j$），是一个我们所要学习的参数。并且$y_j$是一个向量，维度数等于隐因子维度数，每个分量代表对该商品的某一隐因子成分的偏好程度，也就是说对$y_j$求和实际上是将所有产生行为的商品对应的隐因子分量值进行分别求和，最后得到的求和后的向量，相当于是用户对这些隐因子的偏好程度。$|N_u|^{-1/2}$是一个规范化因子。

另外，矩阵分解论文《matrix factorization techniques for recommender systems》中还提到了另一种信息源，即用户画像属性，如年龄、性别、收入等，也可以作为偏好，纳入模型。

TimeSVD++

上述模型都是静态的，但是现实中，物品的流行度会随时间变化，用户的品味也可能随着时间而改变。因此，可以采用TimeSVD++模型基于这种假设建模。该模型的核心思想是：为每个时间段学习一个参数，某个时间段参数使用该时间段数据进行学习。通过建模海量数据，自动发现潜在的时间模式。考虑到数据可能不足的问题，我们想要使用所有数据一起学习，那么可以添加时间距离作为权重。
$$
\hat{r}_{ui} = \mu + b_u(t) + b_i(t) + q_i^T\left(p_u(t) +
|N_u|^{-\frac{1}{2}} \sum_{j \in N_u}y_j\right) \\
$$
上述$b_u(t),b_i(t)$分别是用户和物品偏置随着时间变化的函数，$p_u(t)$是用户隐因子随时间变化的函数。对于这些随时间变化的函数，一种处理是将时间离散化，可以将整个时间窗按照一定粒度进行划分，粒度越小代表随时间变化较大，粒度越大则代表变化较慢。例如处理物品$b_i(t)$，若假定物品的bias在短期内不会很大的改变，那么可以以较大的粒度划分，假设我们选取3个月的交互数据进行建模，整个时间窗口为3个月，以2周为一片，共划分为6片，每个时间$t$，赋予一个$Bin(t)$（即1到6之间的整数），这样就可以把$b_i(t)$分为静态以及动态两部分：$b_i(t)=b_i + b_{i,Bin(t)}$，建模时，相当于需要额外对每个时间片求一个参数$b_{i,Bin(t)}$，以建模物品流行度随时间变化的特性。

如果某个时间$t$数据较少，不能学习到关于该时间$t$的偏置变化参数，那么就不能添加这种和时间相关的参数。一种解决方法是，可以定义关于时间的连续函数，例如处理用户偏置，定义时间偏移量函数：$dev_u(t)=sign(t-t_u).|t-t_u|^\beta$, 其中$t_u$代表该用户所有交互数据的平均时间（是指用户交互的时刻）。$|t-t_u|$代表时间距离。$\beta$是超参数，衡量时间变化影响程度，越大代表受时间影响程度大。则：$b_u(t)=b_u+\alpha_u dev_u(t)$。$\alpha_u$是模型需要为每个用户学习的参数，也就是说参数$\alpha_u$和时间无关，关于该用户的所有数据都能够进行学习，时间因素主要体现在$dev_u(t)$上。

另一种时间函数用到高斯核来衡量时间的相似性。首先获取用户所有交互时间集合。$k_u$个时间点，${t_1^u, …, t_{k_u}^u}$

然后使用公式：
$$
b_u(t) = b_u + \frac{\sum_{l=1}^{k_u} e^{-\gamma|t-t_l^u| } b_{t_l}^u}{\sum_{l=1}^{k_u} e^{-\gamma|t-t_l^u| } }
$$
需要为该用户所有交互时间点学习一个参数$b_{t_l}^u$, 共$k_u$个参数。预测时，使用高斯核计算时间相似性，在所有的时间上计算时间相似性，使用时间相似性对参数$b_{t_l}^u$进行加权。

另外考虑到periodic effects，例如工作日，周末等，可以添加periodic effects参数。
$$
b_u(t) = b_u + \frac{\sum_{l=1}^{k_u} e^{-\gamma|t-t_l^u| } b_{t_l}^u}{\sum_{l=1}^{k_u} e^{-\gamma|t-t_l^u| } } + b_{u, period(t)}
$$

NMF

另外一种方法是非负矩阵分解。是在上述基础上，加入了隐向量的非负限制。然后使用非负矩阵分解的优化算法求解。
$$
\begin{split}p_{uf} &\leftarrow p_{uf} &\cdot \frac{\sum_{i \in I_u} q_{if}
\cdot r_{ui}}{\sum_{i \in I_u} q_{if} \cdot \hat{r_{ui}} +
\lambda_u |I_u| p_{uf}} \\
q_{if} &\leftarrow q_{if} &\cdot \frac{\sum_{u \in U_i} p_{uf}
\cdot r_{ui}}{\sum_{u \in U_i} p_{uf} \cdot \hat{r_{ui}} +
\lambda_i |U_i| q_{if}}\\\end{split}
$$
其中$\hat{r}_{ui}$, 既可以使用FunkSVD求法$\hat{r}_{ui} = q_i^Tp_u $，也可以使用BiasSVD求法$\hat{r}_{ui} = \mu + b_u + b_i + q_i^Tp_u$, 当然也可以改进成使用SVD++的求法。

PMF

概率矩阵分解Probabilistic Matrix Factorization。设有N个用户和M个商品，评分系统用$N \times M$的矩阵$R$表示。基本思路：仍然是矩阵的低秩近似。即$R=U^T V$, 用户和商品之间的关系（即用户对商品的偏好）可以由较少的几个因素的线性组合决定。这也是MF的基本思想。PMF在MF的基础上加上了贝叶斯观点，即认为R是观测到的值，$U,V$描述了系统的内部特征，是需要估计的。

实际上，由于系统噪声存在，不可能做出这样的完美分解，另外$R$包含很多未知元素。所以问题转化为：

  • 对一个近似矩阵进行分解$\hat{R} =U^TV $
  • 要求近似矩阵$\hat{R}$在观测到的评分部分和观测矩阵$R$尽量相似
  • 为了防止过拟合，需要对$U,V$做某种形式的约束

基本假设：

  • 观测噪声（观测评分矩阵$R$和近似评分矩阵$\hat{R}$之差）为高斯分布。
  • 用户属性$U$和商品属性$V$均为高斯分布。

根据第一条假设，有：
$$
P(R_{ij}-U_i^TV_j) \sim N(0,\sigma^2), \\
denotes: P(R_{ij}-U_i^TV_j |0,\sigma^2)
$$
通过平移得到，$P(R_{ij} | U_i^T V_j, \delta^2)$， 根据i.i.d，可以得到评分矩阵的条件概率密度：
$$
P(R|U,V,\sigma^2)=\prod_{i=1}^N\prod_{j=1}^M[N(R_{ij}|U_i^TV_j,\sigma^2)]^{I_{ij}}
$$
这里$U$和$V$是参数，其余看作超参数。$I_{ij}$是指示函数，如果用户$i$对商品$j$评分过，则为1，否则为0.

根据第二条假设，可以写出用户、商品属性的概率密度函数。其中$σ_U,σ_V$是先验噪声的方差，人工设定。
$$
p(U|σ^2_U)=\prod_{i=1}^N N(U_i|0,\sigma^2_UI) \\
p(V|\sigma^2_V)=\prod_{i=1}^M (V_i|0, \sigma^2_V I)
$$
那么根据贝叶斯法则，可以得到用户和商品属性的后验概率：
$$
P(U,V|R,\sigma^2,\sigma_U^2,\sigma_V^2)=P(R|U,V,\sigma^2)P(U|\sigma_U^2)P(V|\sigma_V^2)
$$
采用对数似然估计，代入高斯密度函数可得代价函数如下：
$$
lnP(U,V|R,\sigma^2,\sigma_U^2,\sigma_V^2)=-\frac{1}{2\sigma^2}\sum_{i=1}^N \sum_{j=1}^M I_{ij}(R_{ij}-U_i^TV_j)^2-\frac{1}{2\sigma_U^2}\sum_{i=1}^N U_i^T U_i - \frac{1}{2\sigma_V^2}\sum_{j=1}^M V_j^T V_j \\
-\frac{1}{2}\left (\left( \sum_{i=1}^N \sum_{j=1}^M I_{ij}\right) ln \sigma^2 + NDln \sigma_U^2 + MD ln \sigma_V^2 \right) +C
$$
其中，$D$为隐因子的数量，$C$不受参数影响的常数。当固定超参数后，最大化上述似然等价于最小下述二次优化目标：
$$
E =\frac{1}{2}\sum_{i=1}^N \sum_{j=1}^M I_{ij}(R_{ij}-U_i^TV_j)^2 + \frac{\lambda_U}{2}\sum_{i=1}^N ||U_i||_F^2 + \frac{\lambda_V}{2}\sum_{j=1}^M ||V_j||_F^2 \\
\lambda_U=\frac{\sigma^2}{\sigma_U^2} , \lambda_V=\frac{\sigma^2}{\sigma_V^2}
$$
该模型可以看做是SVD模型的概率化拓展。

最后，为了限制评分的范围，对高斯函数的均值施加logistic函数$g(x)=1/(1+exp(−x))$，其取值在(0,1)之间。最终的能量函数是：
$$
E(U,V)=\frac{1}{2}\sum_{ij}I_{ij}(R_{ij}-g(U_i^TV_j))^2+\frac{\lambda_U}{2}\sum_iU_i^TU_i + \frac{\lambda_V}{2}\sum_jV_j^TV_j
$$
PMF

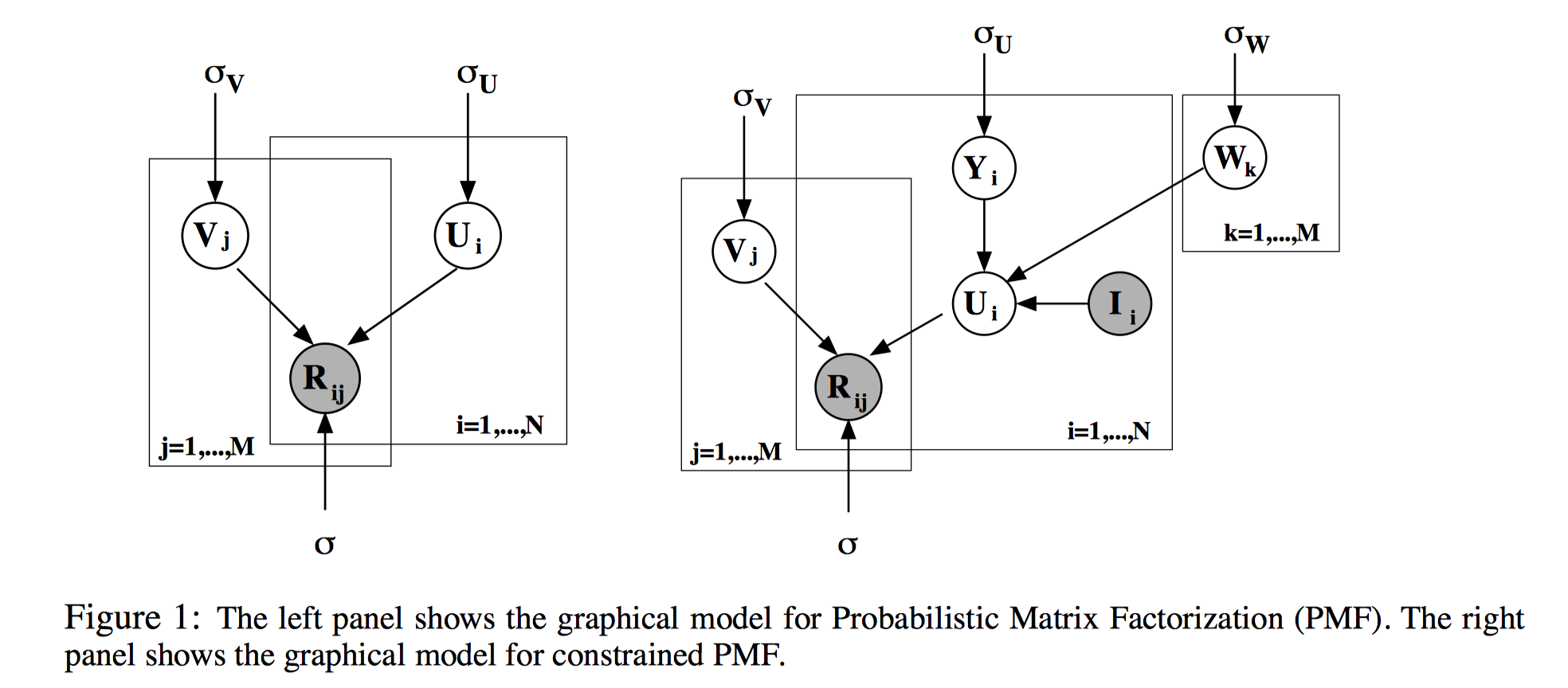
上述所述模型如左图所示。对于右图，是论文提出的受约束的PMF。

简要说明一下Constrained-PMF：用户是否给某个商品打过分”这个信息本身就能一定程度上说明用户的属性。Constrained PMF尝试把$I_{ij}$引入到模型中去。这也是本文的创新之处。

用户属性$U$由两部分组成：和之前相同的高斯部分$Y$，以及$W$用“看过”矩阵$I$加权的结果。
$$
U_i = Y_i + \frac{1}{\sum_kI_{ik}}\sum_kI_{ik}W_k
$$
其中$W$服从方差为$σ_W$, 0均值高斯分布。

WRMF

当数据集是隐式反馈时，应用上述矩阵分解直接建模存在问题。主要有两方面的原因，首先，隐式反馈数据集中只存在正样本，即，$r_{ij}=1, \forall r_{ij} \in \mathcal{R}$. 此时，不能够只使用正样本进行优化，而忽略了未观测样本，否则会造成trivial 但是无用的解，例如把所有的隐向量都预测成向量空间中的同一个点上。其次，不能够把所有的未观测样本都当做是负样本，因为这些未观测的样本既可能是用户不喜欢，也有可能是用户未曾看到但是实际上是喜欢的。为了解决该问题，引入WRMF (weighted regularized matrix factorization). 该方法将所有未观测样本都当做负样本，但是引入了每个样本的权重，来减少这些未知样本的影响力。这些未知样本的权重设置的比观测样本的权重小的多。
$$
min \sum_{r_{ui} \in R_{O} \cup R_{-O}} c_{ui}\left(r_{ui} - p_u^Tq_i \right)^2 +
\lambda\left(||q_i||^2 + ||p_u||^2\right)
$$
其中，$c_{ui}$是样本$r_{ui}$的权重，$R_O$代表观测样本，都为正样本，即$r_{ui}=1$, $R_{-O}$代表未观测样本，都为负样本, 即$r_{ui}=0$。该损失也可以通过PMF推导，此时$c_{ui}^{-1}$即为PMF中评分$r_{ij} \sim \mathcal{N}(p_u^Tq_i, c_{ui}^{-1})$的方差。$c_{ui}$越大，方差越小，置信值越高。

基于排序的推荐算法

参考

BPR: Bayesian Personalized Ranking from Implicit Feedback

Large Scale Image Annotation: Learning to Rank with Joint Word-Image Embeddings

与传统的基于交互数据的point-wise推荐算法不同，基于排序的推荐算法是一种pair-wise learning to rank。这种方法主要适用于隐式反馈数据。

BPR

上述矩阵分解都是针对user-item交互矩阵进行pointwise学习和优化，且大部分针对的是显示反馈数据。而在隐式反馈数据中，目前主流的方法不是通过估计用户对物品的绝对偏好，而是估计用户对不同物品的相对偏好。BPR(Bayesian personalized ranking)就是这样一种思想，利用的是用户对不同物品的相对偏好，使用pair-wise方式的损失进行学习。其核心假设认为，用户对观测样本的偏好比未观测样本的偏好更大。而观测样本之间的偏好差异，以及未观测样本之间的偏好差异不做任何假设。因此，BPR优化如下pairwise ranking loss(pairwise log-sigmoid loss)：
$$
min \sum_{u \in \mathcal{U}} \sum_{(i,j) \in \mathcal{D}_u} -log \sigma(p_u^Tq_i-p_u^Tq_j)+\lambda(||p_u||^2+||q_i||^2)
$$
其中，$\mathcal{D}_u$是用户$u$的Dissimilar物品对集合，即$(i,j) \in \mathcal{D_u}$，则$i$是用户交互过的物品，$j$是用户未交互过的物品。因此，$p_u^Tq_i-p_u^Tq_j$代表用户$u$对二者的相对偏好。该偏好经过sigmoid激活后变为二分类概率，1代表用户$u$对$i$的喜好比$j$高，0代表用户$u$对$i$的喜好比$j$低。优化目标是最大化Dissimilar集合中相对偏好似然值，等价于优化最小化相对偏好负对数似然值。

BPR中提到的排序损失几乎是目前所有最新提出的模型都会利用的损失函数，非常重要！

WARP

WARP全称是Weighted Approximate-Rank Pairwise。WARP主要用于优化Top K推荐。WARP在Hinge Loss基础上考虑了正样本的排序。通常的Top K推荐只关注前K个结果，忽略了对某些排名很低的正样本的惩罚。WARP引入加权排序指标，对那些排名很低的正样本进行惩罚，加大权重，使得模型更关注这些正样本的学习。样本的权重：
$$
w_{ui} = log(rank(u,i)+1)
$$
$rank(u,i)$代表用户$u$推荐结果中物品$i$的排名。越大说明排名越低，则惩罚越高。在Hinge Loss改进：
$$
L_{WARP}=\sum_{u \in \mathcal{U}} \sum_{(i,j)\in \mathcal{D}_u} w_{ui}[1+f_{u,j}-f_{u,i}]_{+}
$$
其中，$f_{u,i}$代表用户$u$对$i$的预测值，$f_{u,j}$同理。可以使用矩阵分解中点乘形式来预测。$[z]_{+}=max(0,z)$是hinge loss损失。推导即，对正样本$i$的预测值要比$j$大一个margin值，即，$f_{u,i}-f_{u,j}>1$, 则：$f_{u,j}-f_{u,i} < -1$, 则：

$f_{u,j}-f_{u,i} + 1< 0$, 对于满足该式的损失为0，否则损失为$f_{u,j}-f_{u,i}+1$，即为$[1+f_{u,j}-f_{u,i}]_{+}$。

优化的时候，作者提出了一种采样的方法来估计$rank(u,i)$。即对每对$(u,i)$, 一直采样，直到有一个样本$j$不满足$f_{u,i}-f_{u,j}>1$， 记采样次数为$N$, $J$为所有物品的个数。则$rank(u,i) \approx \lfloor {\frac{J}{N}} \rfloor$。这个可以直观理解，采样次数$N$越小，说明很容易采到$j$, 即$i$的排名不是很高（$rank(u,i)$值大），因此对其进行惩罚，让模型关注该正样本$i$, 使得优化后该样本排名能高一些。

基于分解机的推荐算法

基于分解机的推荐算法在工业界用的比较多，且该方法通常用于排序阶段训练排序模型。上述提到的多种多样的推荐算法通常会用于召回阶段进行多种多样的推荐，然后在排序阶段对召回结果进一步进行排序，并展示给用户。排序阶段通常会用到物品和用户各种各样的特征以及分类模型。分解机是其中一个很重要的模型之一。我个人理解，这里头的训练数据来源于每次推荐的结果以及最终收集的用户点击/购买/浏览/收藏等反馈行为，根据用户的反馈，可以对推荐的结果打标签，进而可以利用分类模型进行训练。排序模型的好处就在于能够综合不同模型的推荐结果，避免不同模型输出量纲不同等影响，也可以避免穷举计算所有物品和用户偏好匹配度的耗时过程（虽然这部分有很多先进的技术，如近似近邻搜索中的location-sensitive hashing(LSH), 最大点积搜索MIPS）。

FM

分解机FM（Factorization Machine）是由Konstanz大学Steffen Rendle于2010年最早提出的，旨在解决稀疏数据下的特征组合问题。FM设计灵感来源于广义线性模型和矩阵分解。

在线性模型中，我们会单独考察每个特征对Label的影响，一种策略是使用One-hot编码每个特征，然后使用线性模型来进行回归，但是one-hot编码后，一者，数据会变得稀疏，二者，很多时候，单个特征和Label相关性不够高。最终导致模型性能不好。为了引入关联特征，可以引入二阶项到线性模型中进行建模：
$$
y(\mathbf{x}) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n w_{ij} x_i x_j
$$
$x_i,x_j$是经过One-hot编码后的特征，取0或1。只有当二者都为1时，$w_{ij}$权重才能得以学习。然后由于稀疏性的存在，满足$x_i,x_j$都非零的样本很少，导致组合特征权重参数缺乏足够多的样本进行学习。

矩阵分解思想此时发挥作用。借鉴协同过滤中，评分矩阵的分解思想，我们也可以对$w_{ij}$组成的二阶项参数矩阵进行分解，所有二次项参数 $w_{ij}$可以组成一个对称阵$W$，那么这个矩阵就可以分解为 $W=V^TV$，$V$的第 $j$ 列便是第 $j$维特征的隐向量。换句话说，每个参数 $w_{ij}=⟨v_i,v_j⟩$,这就是FM模型的核心思想。因此，FM的模型方程为:
$$
y(\mathbf{x}) = w_0+ \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_i, \mathbf{v}_j \rangle x_i x_j
$$
这里的关键是每个特征都能学习到一个隐向量。这样$w_{ij}=⟨v_i,v_j⟩$不仅仅可以通过$x_i,x_j$进行学习，凡是和$x_i$相关联的特征$h$, 都对学习$x_i$的隐向量$v_i$有所帮助，同理和$x_j$关联的其他特征对学习$x_j$的隐向量$v_j$有所帮助。这样$w_{ij}=⟨v_i,v_j⟩$就有足够多的样本进行学习。

乍看上述式子的时间复杂度为$O(n^2)$，$n$是特征的数量，但是重写上述方程，可以得到：
$$
\begin{aligned}
\sum_{i=1}^{n-1}\sum_{j=i+1}^n(\boldsymbol{v}_i^T \boldsymbol{v}_j)x_ix_j
&= \frac{1}{2}\left(\sum_{i=1}^n\sum_{j=1}^n(\boldsymbol{v}_i^T \boldsymbol{v}_j)x_ix_j-\sum_{i=1}^n(\boldsymbol{v}_i^T \boldsymbol{v}_i)x_ix_i\right)\\
&=\frac{1}{2}\left(\sum_{i=1}^n\sum_{j=1}^n\sum_{l=1}^kv_{il}v_{jl}x_ix_j-\sum_{i=1}^n\sum_{l=1}^k v_{il}^2x_i^2\right)\\\
&=\frac{1}{2}\sum_{l=1}^k\left(\sum_{i=1}^n(v_{il}x_i)\sum_{j=1}^n(v_{jl}x_j)-\sum_{i=1}^nv_{il}^2x_i^2\right)\\
&=\frac{1}{2}\sum_{l=1}^k\left(\left(\sum_{i=1}^n(v_{il}x_i)\right)^2-\sum_{i=1}^n (v_{il}x_i)^2\right)\\
\end{aligned}
$$
可以看出上述的时间复杂度为$O(kn)$。

另外，FM是一种比较灵活的模型，通过合适的特征变换方式，FM可以模拟二阶多项式核的SVM模型、MF模型、SVD++模型等，可以说单纯基于评分矩阵的矩阵分解推荐算法是FM模型的特例。

例如，相比MF矩阵分解中的BiasSVD而言，我们把BiasSVD中每一项的rating分改写为$r_{ui} \sim \beta_u + \gamma_i + x_u^T y_i$，从公式(2)中可以看出，这相当于只有两类特征 $u$ 和 $i$ 的FM模型。对于FM而言，我们可以加任意多的特征，比如user的历史购买平均值，item的历史购买平均值等，但是MF只能局限在两类特征。SVD++与BiasSVD类似，在特征的扩展性上都不如FM。

FFM

FFM（Field-aware Factorization Machine）最初的概念来自Yu-Chin Juan（阮毓钦，毕业于中国台湾大学，现在美国Criteo工作）与其比赛队员，是他们借鉴了来自Michael Jahrer的论文[14]中的field概念提出了FM的升级版模型。通过引入field的概念，FFM把相同性质的特征归于同一个field。也就是说，每个原始数据的特征都可以对应一个field，每个field进行one-hot编码会产生很多新的特征，这些特征归属于同一个field。

FM中每个新特征学习到一个隐向量。而FFM中每个新特征会学习field数量个隐向量。假设样本的 n 个特征属于$ f$ 个field，那么FFM的二次项有 $nf$个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看作FFM的特例，是把所有特征都归属到一个field时的FFM模型。根据FFM的field敏感特性，可以导出其模型方程。
$$
y(\mathbf{x}) = w_0 + \sum_{i=1}^n w_i x_i + \sum_{i=1}^n \sum_{j=i+1}^n \langle \mathbf{v}_{i, f_j}, \mathbf{v}_{j, f_i} \rangle x_i x_j
$$
也就是和不同field的特征计算参数$w_{ij}$时，使用不同的隐向量$v_{i,f_j}$。

目前这两个算法在点击率预测、转化率预测方法取得了很大的成果。

基于Metric Learning的推荐算法

Metric Learning的好处在于学习到的度量符合三角不等式，这样可以传递未知的相似关系，即基于已知的相似关系，传播未知的相似关系。这部分的研究也是目前的推荐系统领域的热门，且大部分会借鉴知识图谱中Knowledge Graph Embeddings，引入Translation Space概念，解决Metric Learning中会将相似点都学习成同一个点的问题。有时间细写。

基于Graph/Network Embedding的推荐算法

目前很多工作把用户，物品交互数据表示成图结构或网络，然后使用基于图或网络的表示学习方法来学习节点或边的语义表达，再将学习到的节点或边的低维表示应用到各自任务中。具体而言，在网络中随机挑选节点，并进行随机游走，采集节点序列，将该节点序列类别word2vec中的语句，初始挑选的节点是target word, 随机游走到的节点是context word，使用SkipGram算法进行学习。最终学习到的节点低维稠密表达，可以用于计算物品之间的相似性，用户和物品之间的相似性等，并应用于推荐系统第一步的召回阶段。学习到的特征表示还可以进一步用于排序阶段，和各种side information一起，作为深度学习模型的输入，进一步学习一个排序模型。代表性的几个工作：

基于深度学习的推荐算法

基于深度学习的推荐算法主要有两种思路。

  • 使用深度学习网络直接拟合效用函数，然后进行推荐，如评分预测、排序预测等。
  • 使用深度学习进行高阶特征提取，集成到传统推荐系统模型当中。这其中又有两种集成方式：要么直接将高阶特征作为传统推荐模型的输入；要么将深度学习作为一个单独的非线性组件，加上传统的线性模型（矩阵分解等）作为另一个组件，同时对推荐任务进行学习和预测。

另外，这里面常用的技术是word embedding，一般对于文本或属性描述数据，先word embedding映射到低维的语义空间，再传入神经网络中建模。原因是因为商品或用户数量太多，通常使用id+onehot来表示的话，那么有多少个商品，输入层神经元就有多少个，这样显然维度太大。故通过embedding技术，能够有效降低输入层神经元数量，同时能够让网络“记住“商品。

按照综述中的分类：

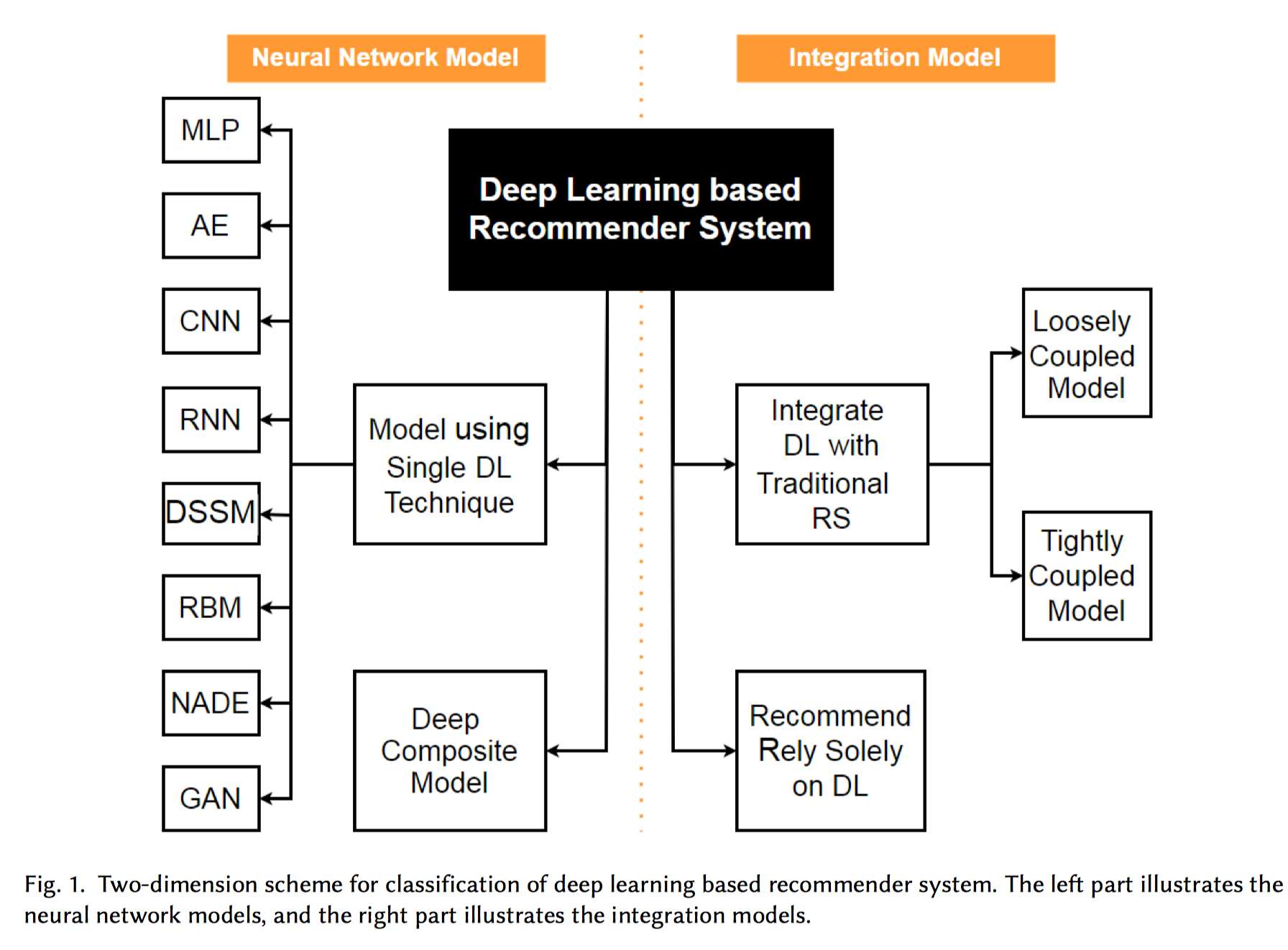
category

有两种分类体系。一种分类方法根据使用的神经网络数量来分类，Neural Network Model，包括使用单一神经网络或多种神经网络。另一种分类方法是根据集成的程度来分类，Integration Model, 包括将神经网络集成到传统推荐系统模型当中，或仅仅使用神经网络进行推荐。

另外，将深度学习模型集成到传统推荐系统模型，又进一步细分成松耦合和紧耦合。 松耦合方式先处理辅助信息，然后，用它为CF提供特征。由于信息的流向是单向的，打分信息无法反馈回来去提取有用的特征。这种方式下，为了提升性能，通常依赖人工提取特征。紧耦合方式，两种方法相互影响，一方面，打分信息指导特征的提取，另一方面，提取出来的特征进一步促进CF的预测能力（例如，稀疏打分矩阵的矩阵因式分解）。两方面的相互影响，使得紧耦合方式可以从辅助信息中自动学习特征，并且能平衡打分信息和辅助信息的影响。这也是紧耦合方法比松耦合方法表现更好的原因。

基于MLP的模型

基于MLP的模型，借助矩阵分解的思想，考察用户和商品二路交互。主要有两种应用方式：

  • 将用户和商品分别映射到同一个隐空间，然后Concatenation后，再一起对隐空间特征进行非线性高阶提取抽象。
  • 用户和商品分别建模，分别进行各自的非线性高阶特征提取，最终输出的时候，借助矩阵分解的思想，使用Element-wise Product方式进行预测。

Neural Collaborative Filtering

动机：在大部分情况下，推荐任务可以看做是用户偏好和商品特征之间的二路交互(a two-way interaction)。

例如上述矩阵分解中，将评分矩阵分解成低维度的隐空间用户矩阵和商品矩阵，基于内容的推荐也是使用用户画像和商品属性之间的相似性进行推荐。故很自然的，可以使用一个dual network来建模用户和商品的二路交互。

Neural Collaborative Filtering (NCF) 就是一个这样的模型，用于捕捉用户和商品之间的非线性关系。

ncf

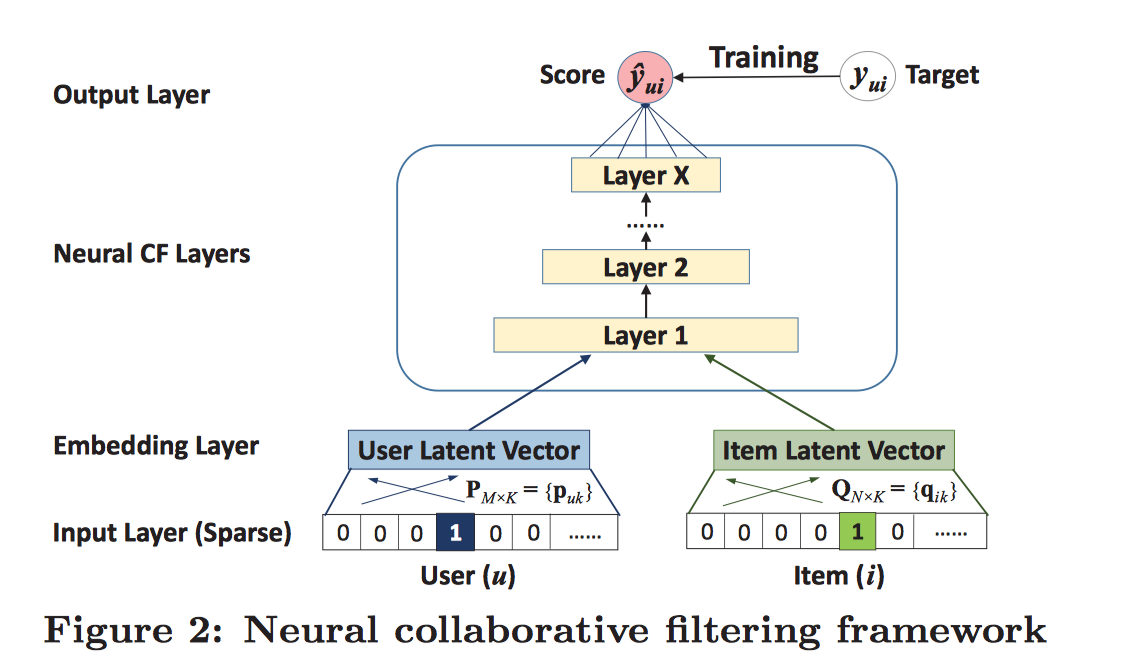
$s_u^{user},s_i^{item}$分别代表用户画像和商品特征，NCF的预测形式化为：
$$
\hat{r}_{ui}=f(P^T. s_u^{user}, Q^T . s_i^{item} | U,V,\theta)
$$
$f (·)$是多层感知网络，$\theta$是网络的参数。这个模型的核心思想是，首先将用户画像和商品特征通过嵌入层映射到同一个隐空间。然后Concatenation后作为网络共同的输入，拟合用户对该商品的评分。拟合的代价函数可以使用平方误差函数，或者使用Sigmoid函数将评分映射到[0,1]区间，再使用交叉熵函数进行优化。

传统的矩阵分解可以看做是NCF的一个特例，原因是P、Q将用户和商品映射到同一个隐空间后，联想到MF中，将原来的User-Item矩阵分解成两个隐空间矩阵的乘积，而这里得到的$U^T. s_u^{user}, V^T . s_i^{item}$向量，同样可以采用向量乘法的方式来拟合原来User-Item矩阵中的$r_{ui}$.故可以将矩阵分解MF纳入到MLP中，形式化成一个更加通用的模型，充分利用MF的线性特性和MLP的非线性特性，提高推荐的质量。模型结构如下：

ncf

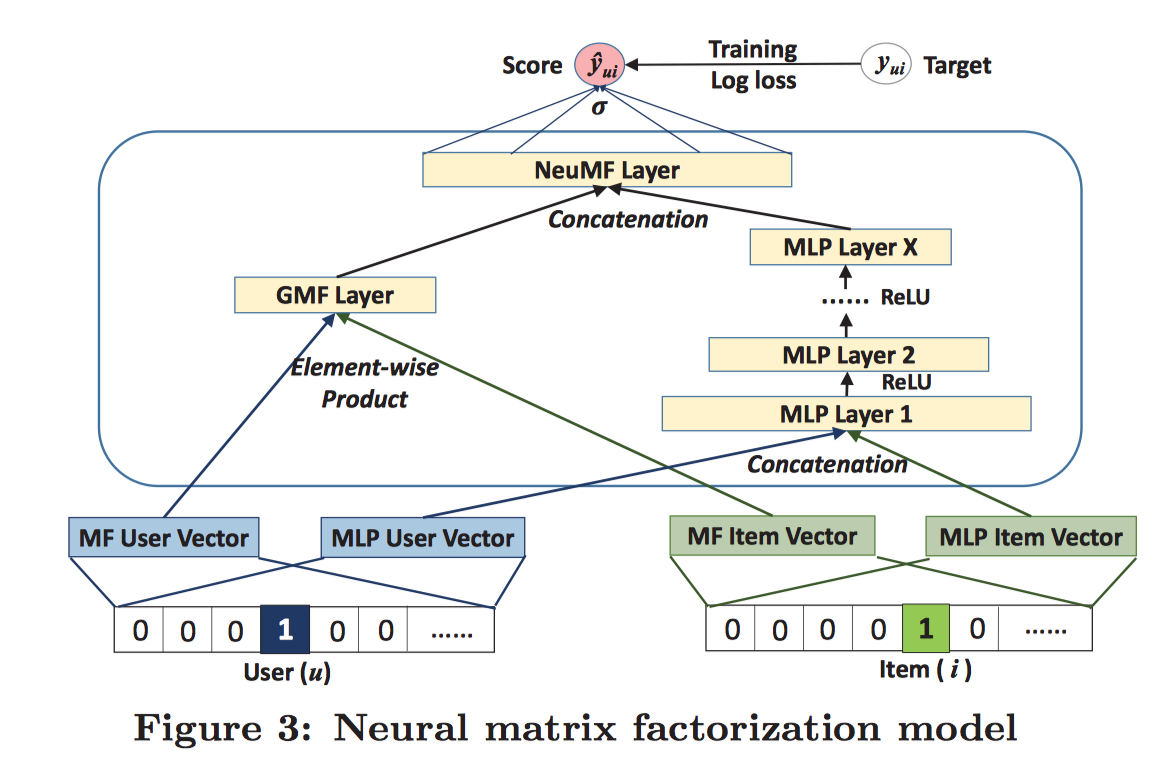
左侧Element-wise Product相当于向量点乘（MF中的方法，预测评分）。右侧的Concatenation利用神经网络的非线性特性。

CCCFNet

上述网络还有其他变种，如跨领域基于内容提升的协同过滤网络Cross-domain Content-boosted Collaborative Filtering neural Network，这种网络仍然是dual network，只不过该网络在最后一层使用点乘的方式来建模User-Item交互矩阵。为了嵌入content information, 作者将dual net分解成两个组件， collaborative filtering factor 和 content information。

ncf

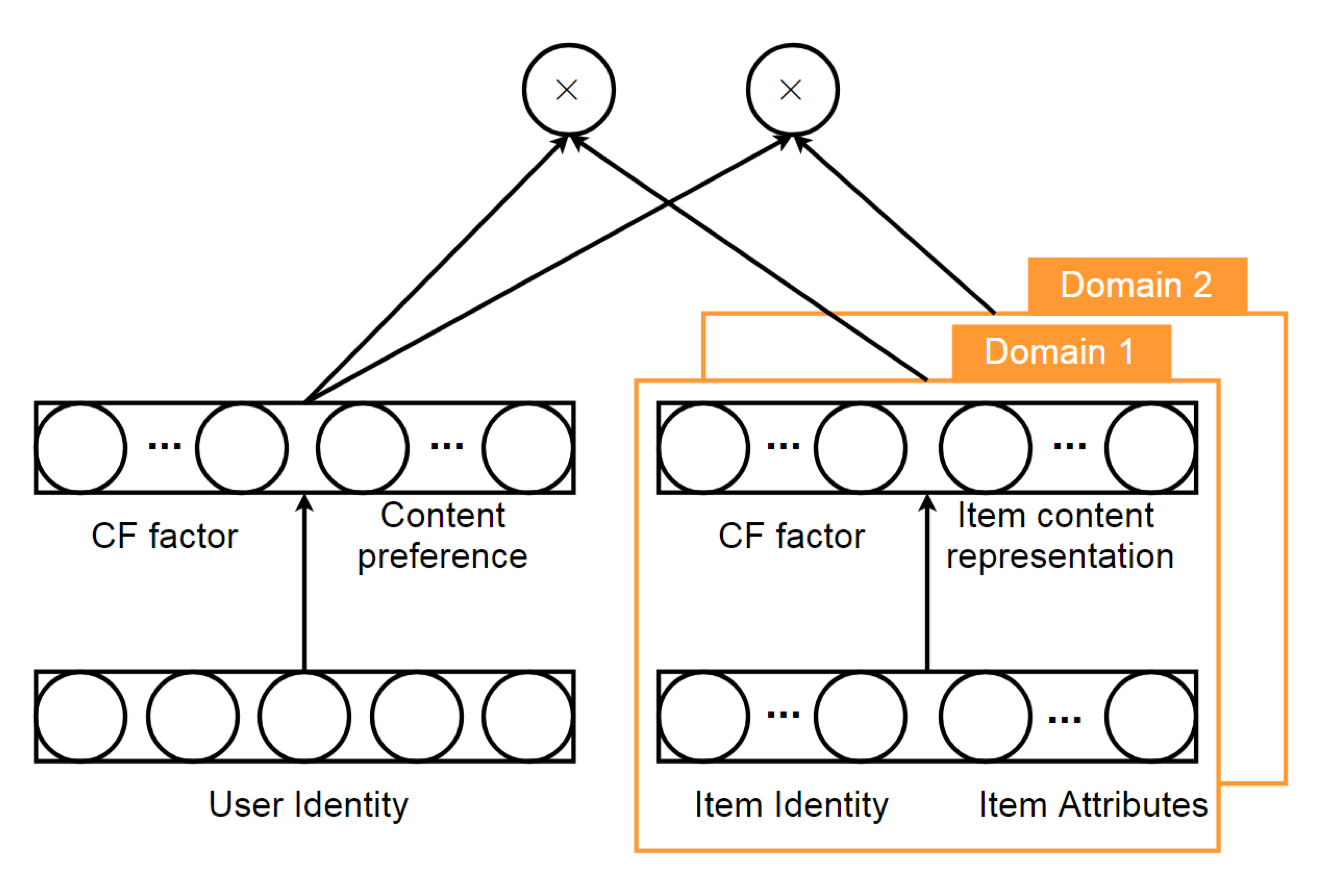
左侧是用户的隐因子和用户画像信息，右侧是商品的隐因子和商品的属性表示。各自concatenation后，再点乘，相当于用户隐向量点乘商品隐向量，以及用户画像信息点乘商品属性表示，前者使用MF的思想，后者使用Content-based的相似度作为效用衡量的思想。图中还可以看出，可以针对不同领域定制右侧的神经网络，得到用户对不同领域的偏好。

Wide & Deep Learning

组成：宽度学习组件使用单层的感知器，可以看做是广义的线性模型；而深度学习组件使用多层感知器。

动机：结合这两种学习技术，能够使得推荐系统同时捕捉到记忆性和泛化性。宽度学习组件能够实现记忆性，记忆性体现着从历史数据中直接提取特征的能力；深度学习组件则能够实现泛化性，泛化性体现着产生更一般、抽象的特征表示的能力。该模型不仅能提高推荐的准确率，同时还能提高推荐的多样性。

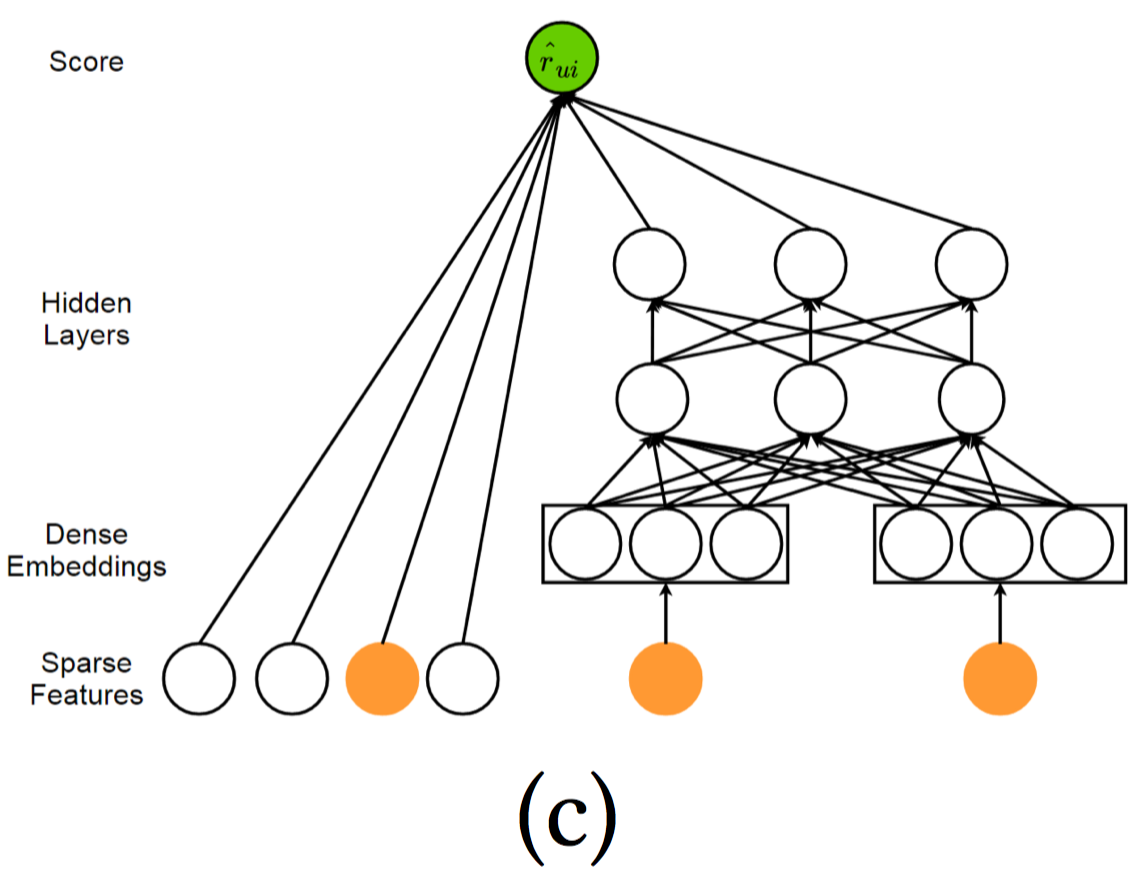
Wide-Deep-Learning

如上图，左侧为宽度组件，使用单层感知器，直接和输出相连接。右侧为深度组件，使用多层感知器。

wide learning 形式化为：$y=W_{wide}^T \{x, \phi(x)\} + b$, $\{x, \phi(x)\}$是concatenated起来的特征，其中$x$是原始特征，$\phi(x)$是手动精心设计的、变换后的特征，例如使用叉乘来提取特征间的关联。这个特征需要精心设计，取决于你希望模型记住哪些重要信息。deep learning形式化为：$a^{l+1} = W^T_{deep} a^{l} + b^{l}$. 二者结合起来，sigmoid激活后：
$$
P(\hat{r}_{ui}=1|x) = \sigma(W^T_{wide}\{x,\phi(x)\} + W^T_{deep}a^{(l_f)}+bias)
$$
上述模型针对的是0/1二值评分的情况。上述手工设计的特征在很大程度上影响模型的性能。一种改进办法是下面改进的端到端模型Deep Factorization Machine(DeepFM).

Deep Factorization Machine

动机：DeepFM是一种端到端模型，解决了上述Wide-Deep Learning中手工设计特征的问题。DeepFM整合了Factorization Machine(FM)和MLP。其中FM能够建模特征间的低阶关联，MLP能够建模特征间的高阶关联。

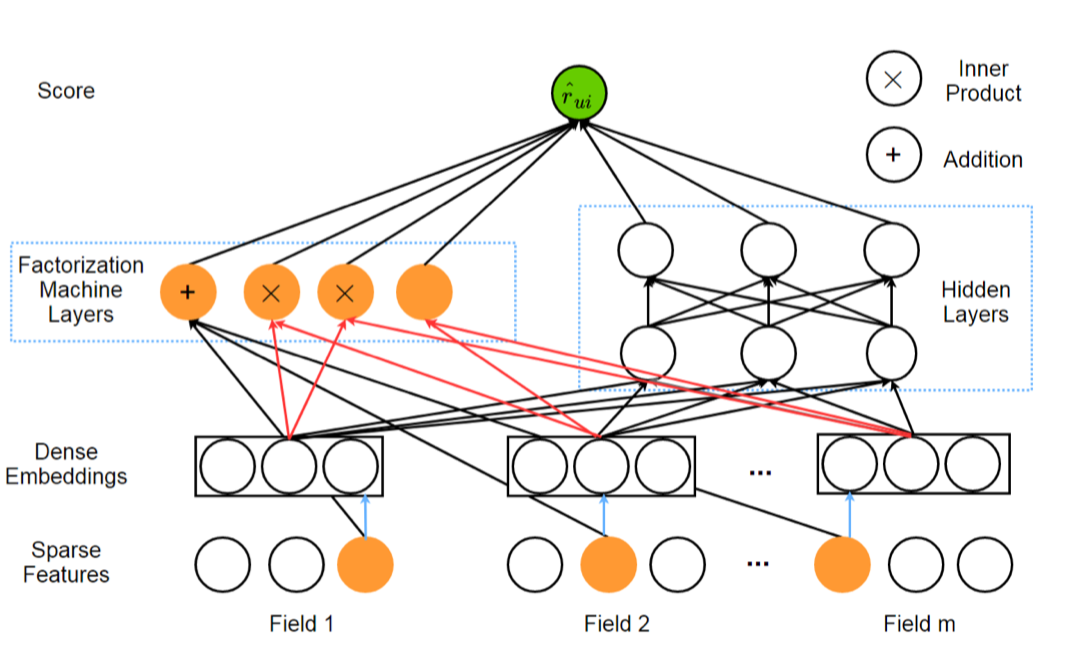
DeepFM

DeepFM不需要特征工程，它将Wide-Deep Learning中的Wide组件使用FM替换。ŒDeepFM的输入是一个m-fields的数据，每条数据由$(u,i)​$数据对组成，$u、i​$分别指的是用户和商品特征。最终预测的结果是：
$$
\hat{r}_{ui} = \sigma(y_{FM}(x) + y_{MLP}(x))
$$
上述FM（Factorization Machine）以及变种FFM，是一种广泛用于点击率、转化率预测和评估的算法。参考 深入FFM原理与实践.

基于AutoEncoder的模型

应用自编码器到推荐系统，主要有两种方式：

  • 使用AutoEncoder学习原数据的低维度特征表示。
  • 直接使用Decoder重构层填充评分矩阵的缺失空格。

AutoRec

动机：将用户或商品的观测向量作为输入，目标是在输出层重构用户或商品的观测向量。

类型：根据输入向量是User还是Item, 分为Item-based AutoRec(I-AutoRec)和User-based AutoRec(U-AutoRec).这里只介绍I-AutoRec, U-AotuRec同理。

形式化：给定商品的观测向量输入$r^{(i)}$, 输出：$h(r^{(i)};\theta)=f(W.g(V. r^{(i)}+\mu) + b)$, 目标是：
$$
\mathop{arg min}_\theta \sum_{i=1}^N ||r^{(i)}-h(r^{(i)};\theta)||_{\mathcal{O}}^2 + \lambda \dot{} Regularization
$$
其中：$\mathcal{O}$代表只使用观测到的评分。

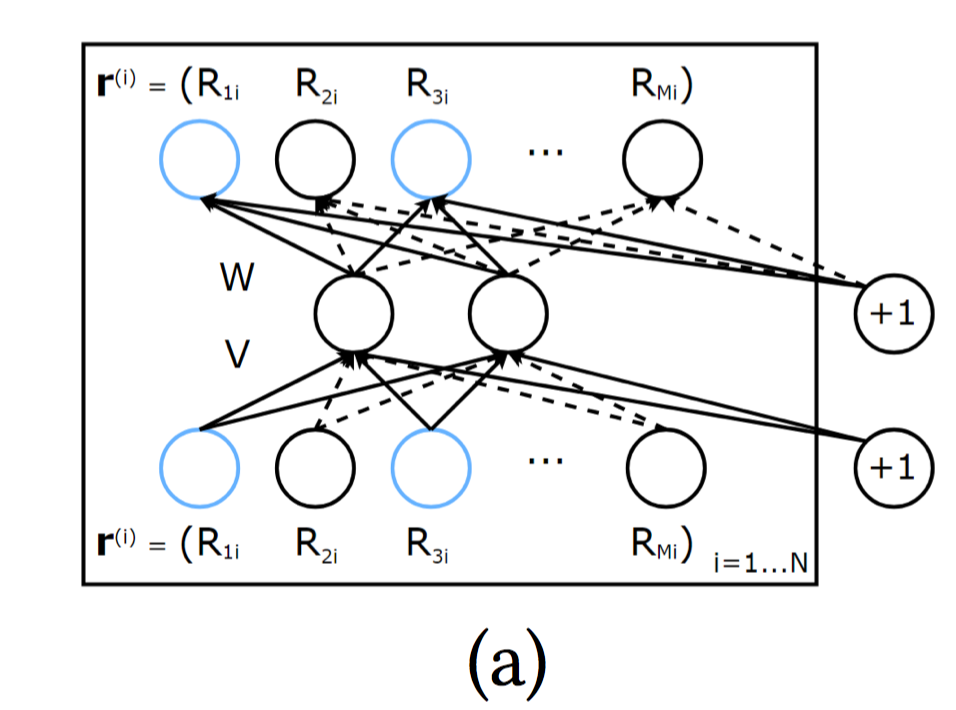
I-autorec

右侧的+1应该指的是偏置项。

Collaborative Filtering Neural network

简称CFN。是AutoRec的扩展。CFN采用了降噪的技术，使得网络更加鲁棒；同时采用了side information，例如用户画像或商品描述，来解决稀疏性和冷启动的问题。

CFN的输入同样是用户或商品的观测向量，故仍然可以分成U-CFN和I-CFN两种。下面介绍I-CFN

CFN首先在随机的抽取部分原始数据，加入高斯噪声或掩码噪声等，然后优化如下目标：
$$
\mathcal{L}=\alpha \left( \sum_{i \in I(\mathcal{O}) \cap I(\mathcal{C})} [h(\tilde{r}^{(i)})-r^{(i)}]^2 \right) +
\beta \left( \sum_{i \in I(\mathcal{O}) \backslash I(\mathcal{C})} [h(\tilde{r}^{(i)})-r^{(i)}]^2 \right) + \lambda \dot{} Regularization
$$
$I(\mathcal{O}) \cap I(\mathcal{C})$代表观测值中加入噪声的部分$；I(\mathcal{O}) \backslash I(\mathcal{C})$代表观测值中未加入噪声的部分。$\alpha，\beta$衡量了二者的重要性。

另外，CFN在每层都加入side information，因此：$h(\tilde{r}^{(i)})=h({\tilde{r}^{(i)}, s_i})=f(W_2 · {g(W_1 · {r^{(i)} , s_i } + µ), s_i} + b)$

CFN

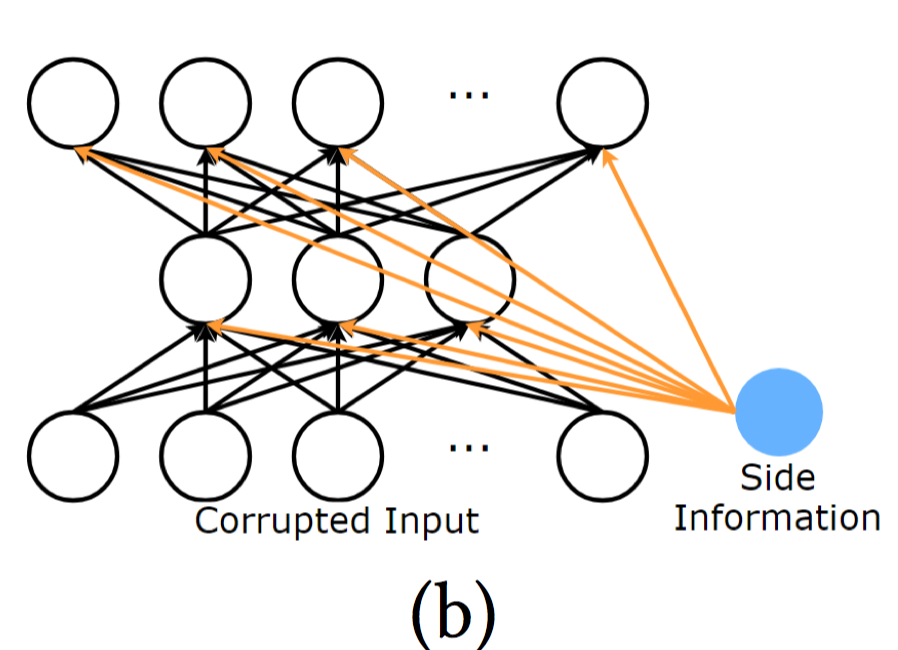
Autoencoder-based Collaborative Filtering

简称ACF。ACF可以直接用于推荐系统，同是也是第一个基于AutoEncoder的推荐模型。

核心思想是，将商品评分向量离散化，例如评分为[1,5]，那么原始的商品评分观测向量可以划分成5个分量。然后作为模型的输入。优化目标同AutoRec。使用RBM进行预训练。

ACF

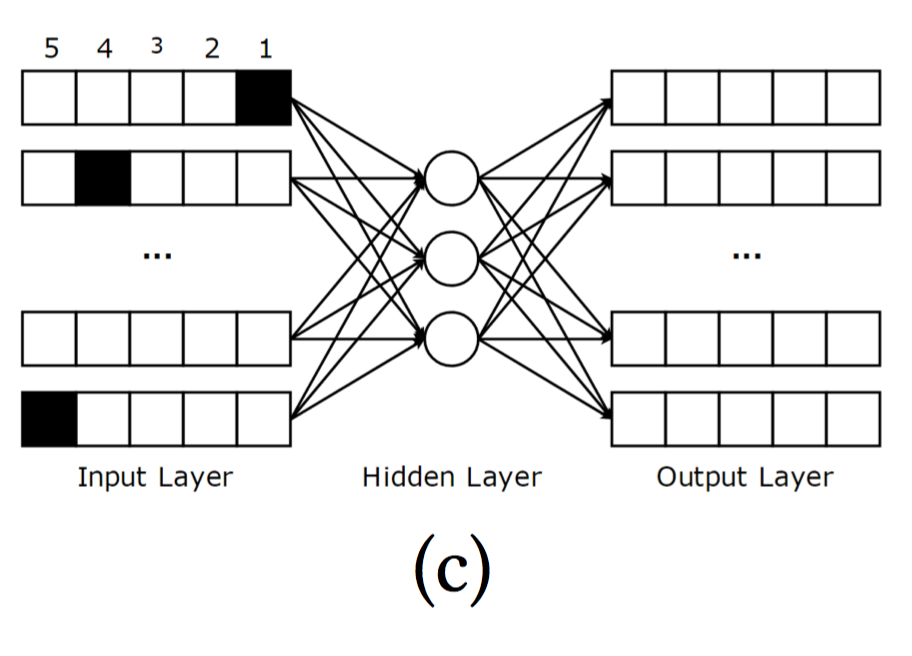
左侧为输入，阴影部分可以代表该用户对商品1评分为1，商品2评分为4。最后的预测，首先将用户的原始评分向量转化成该输入形式，传播到输出层后，最后只要将每个商品向量内的分量累加，即可得到该用户对该商品的评分。

该模型的问题也很突出，只适用于整数型评分，并且切分评分，进一步加重了稀疏性。

Collaborative Denoising Auto-Encoder

简称：CDAE。 前面3种模型主要用于评分预测，CDAE则用于排序预测。CDAE的输入是用户向量，即观测到的用户隐式反馈$r_{pref}^{(u)}$，代表着对每个商品的偏好，若分量为1，则代表对相应商品感兴趣，否则为0。输入同样使用高斯噪声。

CDAE

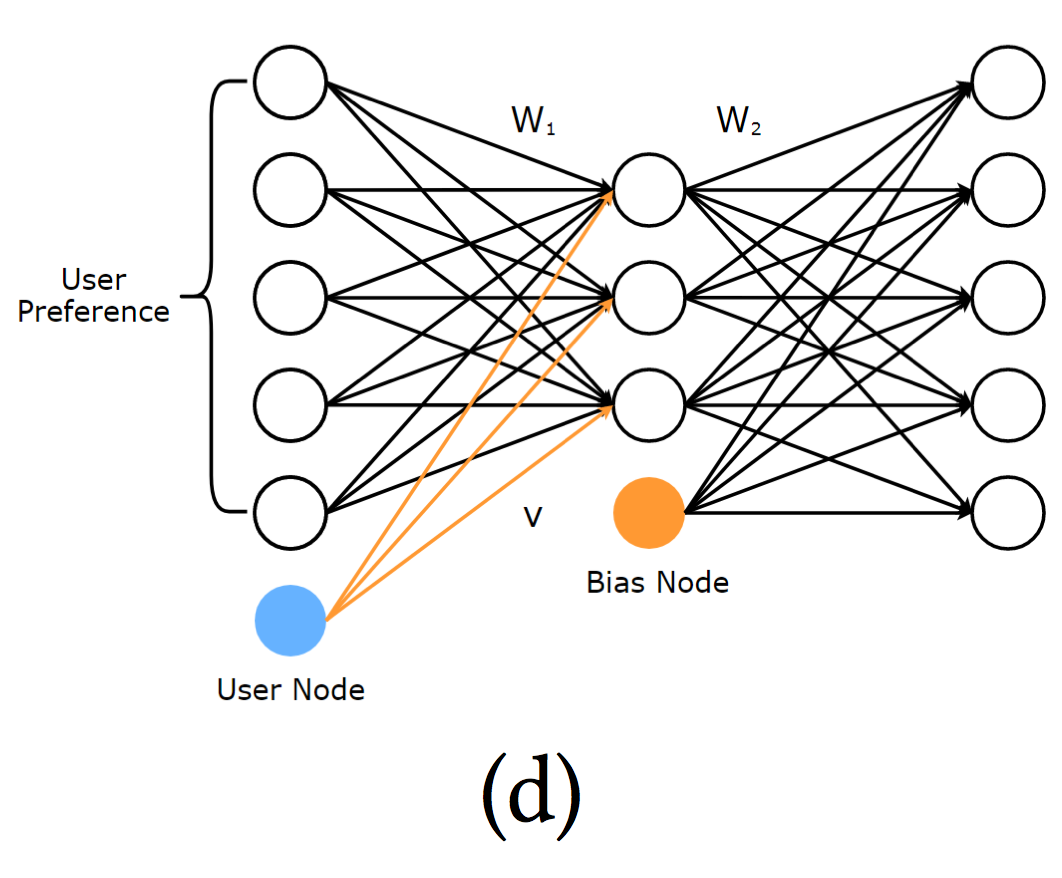
重构为：$h(\tilde r^{(u)}_{pref} ) = f (W_2 · g(W_1 · \tilde r_{pref}^{(u)} + V_u + b_1 ) + b_2)$

重构目标：
$$
\mathop{arg min}_{W_1,W_2,V,b_1,b_2} \frac{1}{M} \sum_{u=1}^M E_{p(\tilde{r}^{(u)}_{pref} |r^{(u)}_{pref}) }
[\ell(\tilde{r}^{(u)}_{pref} , h(\tilde r^{(u)}_{pref} ) )] + λ · Regularization
$$

Collaborative Deep Learning

CDL是一种紧耦合的、基于CTR、Stacked Denoising Autoencoders、多层贝叶斯模型等方式的推荐模型。

其中，协同主题回归（CTR）是一种主流的紧耦合方法。它是一个整合了Topic model，LDA，CF，概率矩阵分解（PMF）的概率图模型。

实际上CDL就是把CTR模型和深度学习模型SDAE集成起来，形成一个多层贝叶斯模型。作者用贝叶斯法则表征栈式自编码器SDAE，用深度学习的方式表示content information和rating matrix，使两者双向相互影响。

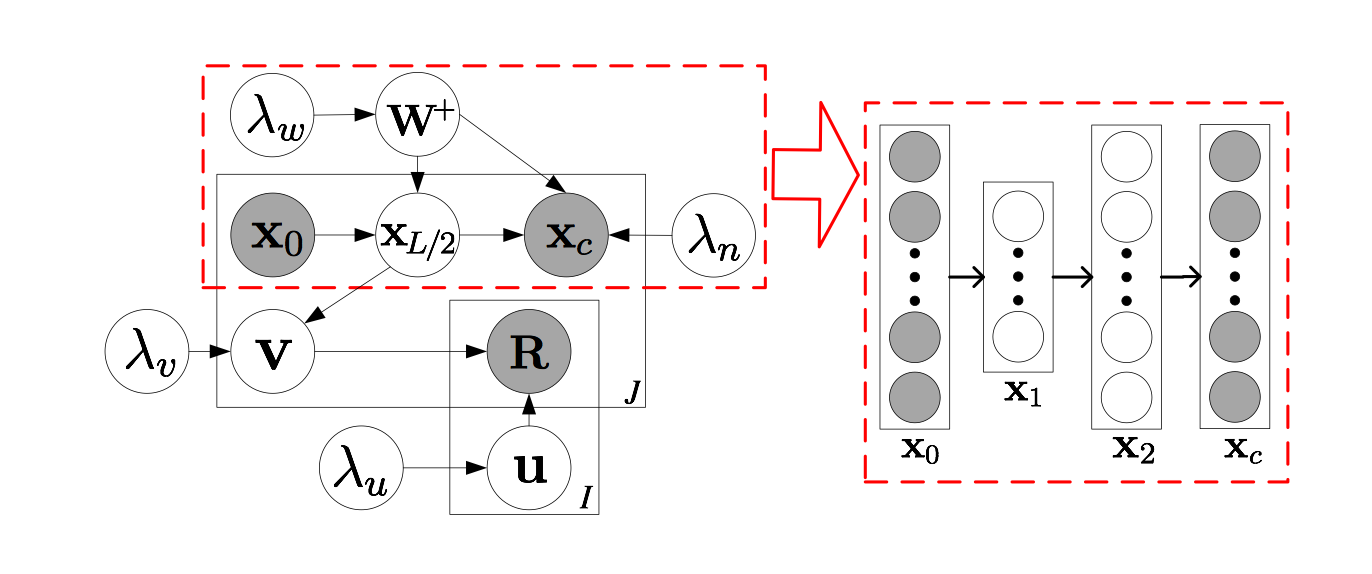
cdl-net

根据上图，左下角实际上就是PMF的模型框架，CDL使用栈式编码器提取特征，前L/2是编码器，后L/2是解码器，

使用L/2层的输出$X_{L/2}$作为提取到的特征作用于商品隐矩阵$V$。

具体的还要进一步研究论文《Collaborative Deep Learning for Recommender System》。

基于CNN的模型

核心思路主要是使用CNN模型来进行特征抽取。

A‚ttention based CNN

最早用于微博的标签推荐。将推荐任务看做是一个多分类问题。模型包括一个全局通道global channel和局部关注通道local attention channel. global channel由卷积核和max-pooling层组成，所有的单词在global channel进行编码。而Local attention channel有一个attention layer, 使用给定的窗口大小$h$和阈值$\eta$来选择信息量比较大的单词。

令 $w_{i:i+h}$ 表示单词 $w_i , w_{i+1} ,…,w_{i+h}$ . 该窗口Œ中间单词 $(w _{(2i+h−1)/2})$ 的分数根据如下计算：
$$
s_{(2i+h-1)/2} =g (W* w_{i:i+h}+b)
$$
只有分数大于$\eta$的才进行保留。

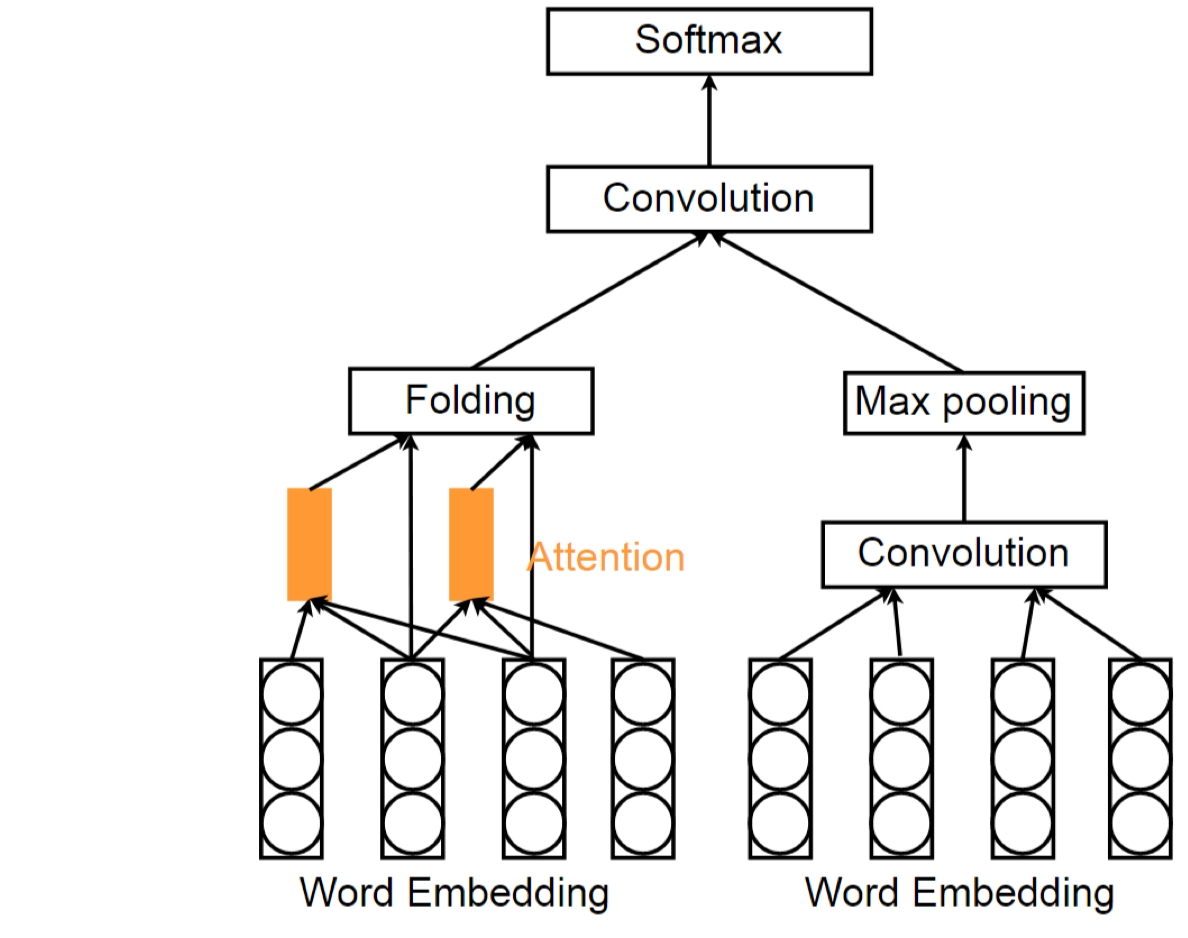
AttentionCNN

如上图，左侧为Local Attention Channel, 右侧为Global Channel.

Personalized CNN

最早用于个性化标签推荐。利用CNN抽取图像patches的视觉特征，然后加入User information，来产生更加个性化的推荐。

DeepCoCNN

这是一种紧耦合的模型，将CNN集成到FM模型中。DeepCoNN采用两种并行的CNN网络来分别建模用户评论文本中的用户行为和商品评论文本中的商品属性。 然后在输出层，使用Factorization Machine来捕捉用户和商品的交互，用于评分预测。

具体的，首先使用word embedding技术将评论文本映射到一个低维度的语义空间，同时保持单词序列的信息。抽取到的评论表示再传入到卷积网络，最终用户网络和商品网络的输出再concatenate连接后，作为Factorization Machine的输入。

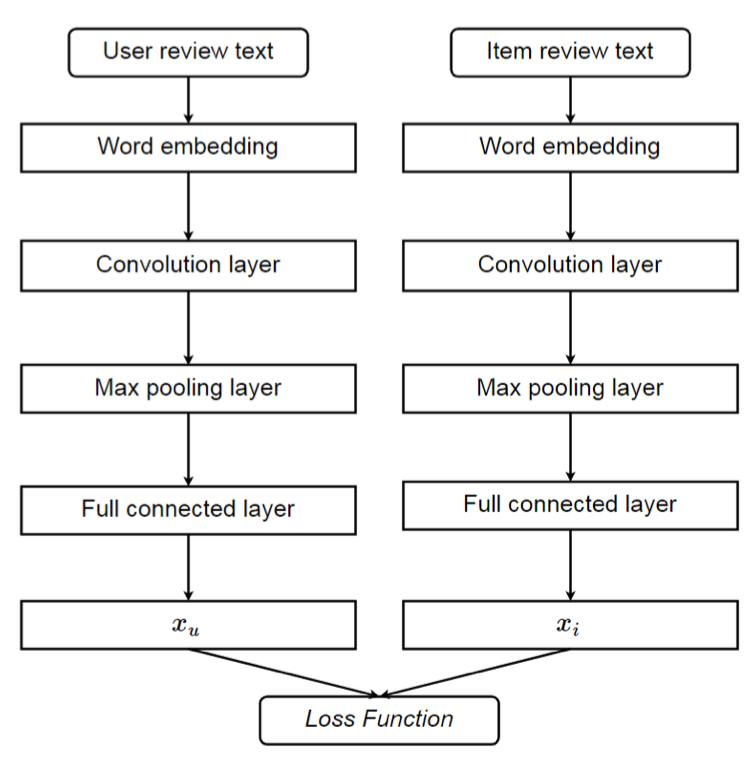
deepconn

ConvMF

ConvMF也是一种紧耦合的模型，将CNN集成到PMF模型中。ConvMF使用CNN来学习高阶商品特征表示，然后作用到商品$V$矩阵。

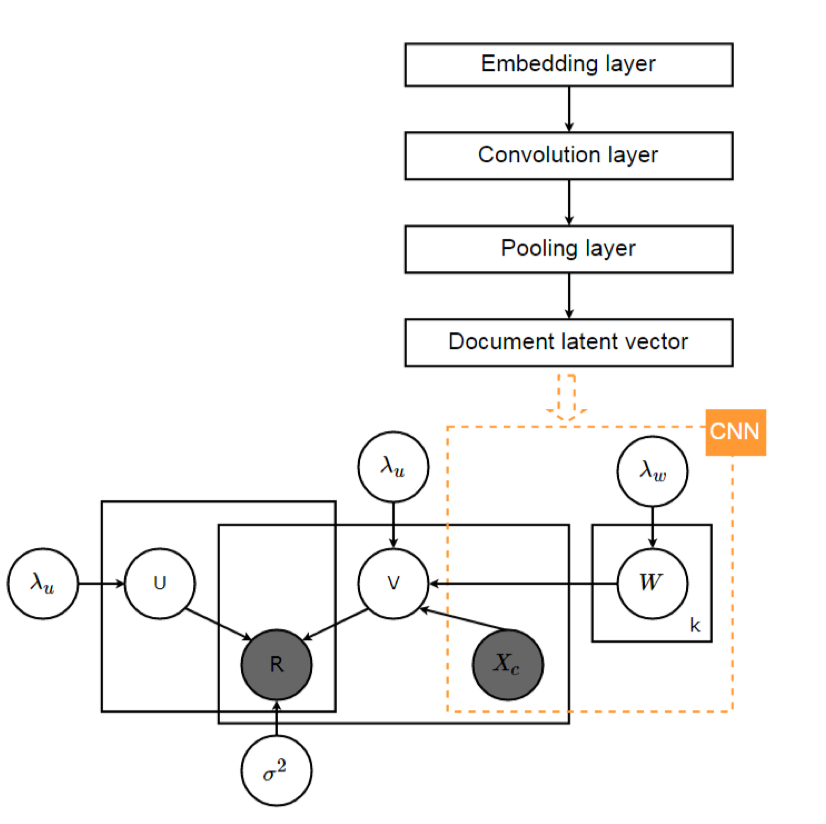
ConvMF

该模型类似CDL。只不过将CDL中通过SADE自动提取的特征$X^T_{L/2,i*}$使用CNN提取的特征$cnn(W,X_i)$替换，这些特征将作用于V矩阵。

如上图所示，左下角是PMF模型的框架，右侧引入CNN，提取商品属性的高阶特征，作用于V矩阵。

其他

其他的还要基于RNN、GAN、RBM、NADE等模型。以及不同深度网络组合方式的模型。

  • RNN：

一种是session-based RNN. 也就是根据session会话，作为时序信息来建模。例如可以根据session中，某个时刻，商品是否active来构建商品向量，是，则分量为1，否则为0。这样不同时刻，就有不同的商品向量，作为一个时序特征，传入到RNN建模。

  • GAN：

生成对抗网络可以这样重新定义推荐任务。假设要根据用户查询来推荐文档。生成模型的任务是根据指定的查询来产生相关的文档，而判别模型则用于预测给定的查询,文档对的相关性分数。生成模型的目标是根据查询产生和真实情况最相近的文档，用于迷惑判别模型，使得其很难判别出该文档是真实的用户需求的文档，还是生成模型推荐的文档。

后续

不断更新中。。。

参考

最后，欢迎大家关注我的微信公众号，蘑菇先生学习记。会定期推送关于算法的前沿进展和学习实践感悟。

公众号

坚持原创技术分享，您的支持将鼓励我继续创作！