LDA主题模型
LDA（Latent Dirichlet Allocation）是基于贝叶斯模型的，涉及到贝叶斯模型离不开“先验分布”，“数据（似然）”和”后验分布”。在贝叶斯学派这里：$P(\theta|X) \propto P(X|\theta)P(\theta)$, 两边取对数，$ln P(\theta|X)=lnP(X|\theta)+lnP(\theta)$, 可以简单理解为：先验分布 + 数据（似然）= 后验分布 。先验分布是我们在观察数据之前对模型的先验知识，通过观察数据之后，我们会对先验模型进行调整优化，使得更加符合真实模型，调整后就得到后验分布。
数据似然是指数据服从的分布，通常是以条件概率密度函数的形式给出。对于先验分布，我们要引出共轭先验的概念。我们考虑增量更新模型的参数。我们的目的是，在不断更新模型的过程中，模型的先验分布形式不会改变。也就是说观察到某个数据，按照贝叶斯公式计算了后验分布，并使得后验分布最大化；在下一次新的数据到来时，前面得到的后验分布能够作为此次更新的先验分布，也就是说先验分布和后验分布的形式应该是一样的，这样的先验分布就叫做共轭先验分布。
二项分布和Beta分布
对于二项分布：
$$
Binom(k|n,p) = {n \choose k}p^k(1-p)^{n-k}
$$
这个分布可以理解为，在给定事件出现的概率$p$和试验的次数$n$，求该事件出现$k$次的概率。这里的核心参数是$p$。$n, k$可以理解为样本数据，即每次实验$n$次，观察事件出现的次数$k$, 得到一个样本。可以对照数据似然理解$P(X|\theta)$。可以通过大量的实验样本和似然估计，来估计$p$，$E[p]=\frac{k}{n}$。
二项分布的共轭先验是Beta分布，参数$p$的Beta先验分布如下：
$$
Beta(p|\alpha,\beta) = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{\alpha-1}(1-p)^{\beta-1}
$$
仔细观察Beta分布和二项分布，可以发现两者的密度函数很相似，区别仅仅在前面的归一化的阶乘项。另外有，$E[p]=\frac{\alpha}{\alpha+\beta}$， $\alpha、\beta$可以认为是伪计数，$\alpha$是事件发生的次数，$\beta$是事件不发生的次数。注意，这里的参数和正常讲的beta分布的参数不一样，这里的参数$p$实际上是我们的应用需要求解的参数，而对于beta分布而言，参数实际上是$\alpha，\beta$，而$p$实际上是样本$X$，即定义域，取值为$(0,1)$。对于我们的应用，我们需要根据Beta分布来采样样本$p$（对我们的应用而言, $p$是参数）。
参数$p$的后验分布的推导如下：
$$
\begin{align}P(p|n,k,\alpha,\beta) & \propto P(k|n,p)P(p|\alpha,\beta) \\& = P(k|n,p)P(p|\alpha,\beta) \\& = Binom(k|n,p) Beta(p|\alpha,\beta) \\&= {n \choose k}p^k(1-p)^{n-k} \times \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}p^{\alpha-1}(1-p)^{\beta-1} \\& \propto p^{k+\alpha-1}(1-p)^{n-k + \beta -1} \end{align}
$$
将上式归一化，得到关于参数$p$的后验概率分布，可以看出服从Beta分布。
$$
P(p|n,k,\alpha,\beta) = \frac{\Gamma(\alpha + \beta + n)}{\Gamma(\alpha + k)\Gamma(\beta + n - k)}p^{k+\alpha-1}(1-p)^{n-k + \beta -1}
$$
两边取对数，则可以概括为：
$$
Beta(p|\alpha,\beta) + BinomCount(k,n-k) = Beta(p|\alpha + k,\beta +n-k)
$$
这个后验分布很符合直觉。先验分布基础上，实验了$n$次，事件发生的次数共为$k$次，那么相当于现在事件发生的次数为$\alpha+k$，不发生的次数为$\beta+(n-k)$.
多项分布与Dirichlet 分布
上述分布都是针对2种类别，因此只需要一个参数$p$。对于多种类别的情况，就需要将二维拓展到多维。对于二项分布，我们指定了事件的概率$p$，和发生的次数$k$。同理，对于多项式分布，我们可以指定不同事件发生的概率，以及各自对应的次数。例如对于三项分布：
$$
multi(m_1,m_2,m_3|n,p_1,p_2,p_3) = \frac{n!}{m_1! m_2!m_3!}p_1^{m_1}p_2^{m_2}p_3^{m_3}
$$
这里的参数就是$p_1,p_2,p_3$， 且$p_1+p_2+p_3=1$， 2个自由度，使用向量$\vec{p}$来表示。这里的$m_1,m_2,m_3,n$就是样本，满足$m_1+m_2+m_3=n$，如果指定了n，则为2个自由度，使用向量$\vec{m}$表示。整个三项分布可以理解为，共实验$n$次，则事件1出现$m_1$次，事件2出现$m_2$次，事件3出现$m_3$次的概率。可以对照数据似然理解$P(X|\theta)$。多维的多项式分布记做：$multi(\vec m| n, \vec p)$。
多项分布的共轭先验分布是狄利克雷(以下称为Dirichlet )分布。也可以说Beta分布是Dirichlet 分布在二维时的特殊形式。从二维的Beta分布表达式，我们很容易写出三维的Dirichlet分布如下：
$$
Dirichlet(p_1,p_2,p_3|\alpha_1,\alpha_2, \alpha_3) = \frac{\Gamma(\alpha_1+ \alpha_2 + \alpha_3)}{\Gamma(\alpha_1)\Gamma(\alpha_2)\Gamma(\alpha_3)}p_1^{\alpha_1-1}(p_2)^{\alpha_2-1}(p_3)^{\alpha_3-1}
$$
上述就是三维参数向量$\vec{p}$的Dirichlet先验分布形式。
对于多维分布，写作$Dirichlet(\vec p| \vec \alpha)$。
$$
Dirichlet(\vec p| \vec \alpha) = \frac{\Gamma(\sum\limits_{k=1}^K\alpha_k)}{\prod_{k=1}^K\Gamma(\alpha_k)}\prod_{k=1}^Kp_k^{\alpha_k-1}
$$
多项分布和Dirichlet分布也满足共轭关系：
$$
Dirichlet(\vec p|\vec \alpha) + MultiCount(\vec m) = Dirichlet(\vec p|\vec \alpha + \vec m)
$$
Dirichlet分布的期望：
$$
E(\vec{p}) = (\frac{\alpha_1}{\sum\limits_{k=1}^K\alpha_k}, \frac{\alpha_2}{\sum\limits_{k=1}^K\alpha_k},…,\frac{\alpha_K}{\sum\limits_{k=1}^K\alpha_k})
$$
同样，对于通常的$Dirichlet$分布，其参数是$\vec{\alpha}$， $\vec{p}$实际上是样本$X$， 定义域为$(0,1)$。而对于我们的应用而言，$\vec{p}$是要求解的参数（如文档主题的概率分布，后续会看到该参数不需要显示地进行求解，$p$只是中间产物，用于解释数据生成过程，优化的时候，还是求解$\vec{\alpha}$的贝叶斯估计），我们需要根据Dirichlet分布采样样本$\vec{p}$。
LDA主题模型
我们的问题是, 有$M$篇文档，对应的第$d$个文档中有$N_d$个词。
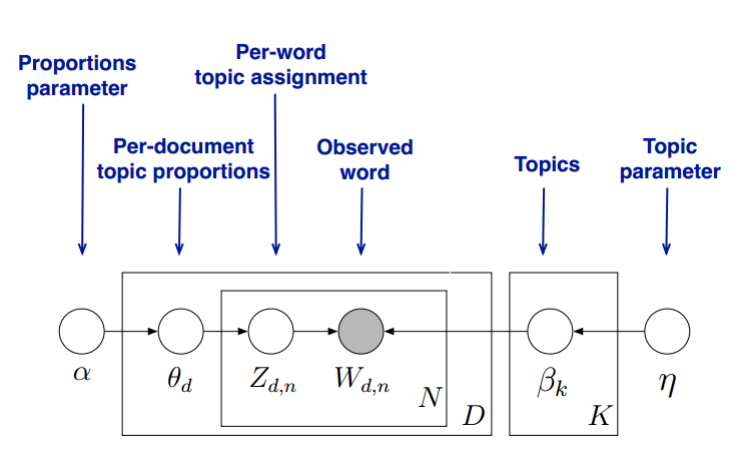
我们的目标是找到每一篇文档的主题分布和每一个主题中词的分布。在LDA模型中，我们需要先假定一个主题数目$K$，这样所有的分布就都基于K个主题展开。模型结构如下：
具体的生成数据过程如下：
对于每一篇文档$d$，重复如下过程:
- 首先确定生成该文档的主题分布（文档-主题分布）。
LDA假设文档主题的先验分布是Dirichlet分布，即对于任一文档$d$, 其主题分布$θ_d$为：
$$
\theta_d = Dirichlet(\vec \alpha)
$$
其中，$α$为分布的超参数，是一个$K$维向量。可以认为是该文档$d$中$K$个主题的伪计数。$\theta_d$对应的是$K$个主题的概率向量，也就是上文中的$\vec{p}$，是需要根据Dirichlet分布，通过采样采到, 这个参数$\theta_d$就是数据似然分布(多项式分布)中的参数。每个主题代表1个事件，共$K$个事件。
对文档$d$中的第$n$个词，需要确定生成该词的具体主题编号。
我们从主题分布$θ_d$中抽样主题编号$z_{dn}$的分布为：
$$
z_{dn} = multi(\theta_d)
$$
也就是说，我们得到了该篇文档$K$个主题中每个主题（所有事件）的概率向量$\theta_d$, 那么在生成该篇文档某一个词汇的时候，需要先确定具体使用哪一个主题来生成该词汇。可以根据多项式分布 $multi(\theta_d)$抽样一个主题（1个事件）。
确定构成该主题的词汇分布（主题-词汇分布）。
上述得到了具体某个主题，我们需要确定该主题的词汇分布，主题使用词来刻画。LDA假设主题中词的先验分布也是Dirichlet分布，即对于任一主题$k$, 其词分布$β_k$为：
$$
\beta_k= Dirichlet(\vec \eta)
$$
其中，$\eta$为分布的超参数，是一个$V$维向量。$V$代表词汇表里所有词的个数，可以认为是表征该主题的所有词的伪计数，每个词代表1个事件，共$|V|$个事件。同样，根据Dirichlet分布，需要采样表征该主题的每个词的概率向量$\beta_k$.
确定最终生成的词编号。
对于得到的主题编号，需要确定最终生成哪一个词，该词$w_{dn}$满足如下多项式分布，$\beta_{z_{dn}}$是上述得到的主题$z_{dn}$不同词的概率分布。
$$
w_{dn} = multi(\beta_{z_{dn}})
$$
同样需要根据上述多项式分布，采样一个词（1个事件），作为最终生成的词。
理解LDA主题模型的主要任务就是理解上面的这个模型。
这个模型里，我们有$M$个文档主题的Dirichlet分布，而对应的数据有$M$个主题编号的多项分布，这样$(\alpha→θ_d→\vec{z}_d )$就组成了Dirichlet-Multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的文档主题后验分布。
如果在第$d$个文档中，第$k$个主题(根据某个词，属于哪种主题权重最大确定)的个数为：$n^{(k)}_d$, 则对应的多项分布的计数可以表示为:
$$
\vec n_d = (n_d^{(1)}, n_d^{(2)},…n_d^{(K)})
$$
利用Dirichlet-Multi共轭，得到$θ_d$的后验分布为：
$$
Dirichlet(\theta_d | \vec \alpha + \vec n_d)
$$
同样的道理，对于主题词汇的分布，我们有$K$个主题词汇的Dirichlet分布，而对应的数据有$K$个主题编号的多项分布，这样$(\eta \rightarrow \beta_k \rightarrow \vec{w}_{k})$就组成了Dirichlet-Multi共轭，可以使用前面提到的贝叶斯推断的方法得到基于Dirichlet分布的主题词的后验分布。
如果在第k个主题中，第$v$个词的个数为：$n^{(v)}_k$, 则对应的多项分布的计数可以表示为:
$$
\vec n_k = (n_k^{(1)}, n_k^{(2)},…n_k^{(V)})
$$
利用Dirichlet-Multi共轭，得到$β_k$的后验分布为：
$$
Dirichlet(\beta_k | \vec \eta+ \vec n_k)
$$
由于主题产生词不依赖具体某一个文档，因此文档主题分布和主题词分布是独立的。理解了上面这$M+K$组Dirichlet-Multi共轭，就理解了LDA的基本原理了。总结起来，每篇文档的主题分布是各自独立的，$M$篇文档就有$M$个文档主题分布; 而主题的词汇分布是所有文档共享的，假设有$K$个主题，则主题的词汇分布就有$K$个。
算法求解
现在的问题是，基于这个LDA模型如何求解我们想要的每一篇文档的主题分布和每一个主题中词的分布呢？
一般有两种方法，第一种是基于Gibbs采样算法求解，第二种是基于变分推断EM算法求解。
问题的关键在于主题$\vec{z}$是未知的，无法确定某一个词所属的主题，也就无法确定一篇文档当中不同主题的计数情况，即文档的主题分布，也无法得到主题的词分布。因此问题的关键在于如何确定一个词所属的主题，即$p(z_i|w_t)$，即主题与词的对应关系。
Gibbs采样
Gibbs采样的核心是求解某个词所属的主题的条件概率。为了求解该条件概率，可以考虑从词和主题的联合概率$p(\vec{w}, \vec{z})$入手，假如该联合概率已知，则条件概率的求解很容易，除以常数$p(w)$即可。
更进一步，我们要求解的条件概率是某一个词$w_i$所属的主题分布$z_i$，即：$p(z_i=k|\vec{w}, \vec {z}_{\neg i})$， $\vec{z}_{\neg i}$代表除$w_i$之外的其它词的主题分布。我们只要能够求解出该主题分布的形式，我们就可以用Gibbs采样依次去采样所有词的主题，当Gibbs采样收敛后，即可得到所有词的采样主题，该主题作为该词的最终所属主题。最后，利用所有采样得到的词和主题的对应关系，我们就可以得到每个文档词主题的分布$θ_d$和每个主题中所有词的分布$β_k$，具体而言，根据词和主题的对应关系，统计一篇文档中不同词所属主题的计数，就能计算出该篇文档的主题分布；同样，对于某个主题，统计属于该主题不同词的计数，就能计算出该主题的词分布。
这里忽略具体推导，首先得到除去词$w_i$之外，两个$Dirichlet$分布的参数在贝叶斯框架下的参数估计：（对参数求积分得到）
$$
\hat{\theta}_{dk} = \frac{n_{d, \neg i}^{k} + \alpha_k}{\sum\limits_{s=1}^Kn_{d, \neg i}^{s} + \alpha_s} \\\\
\hat{\beta}_{kt} = \frac{n_{k, \neg i}^{t} + \eta_t}{\sum\limits_{f=1}^Vn_{k, \neg i}^{f} + \eta_f}
$$
推导条件概率公式：
$$
\begin{align} p(z_i=k| \vec w,\vec z_{\neg i}) & \propto p(z_i=k, w_i =t| \vec w_{\neg i},\vec z_{\neg i}) \\& = \int p(z_i=k, w_i =t, \vec \theta_d , \vec \beta_k| \vec w_{\neg i},\vec z_{\neg i}) d\vec \theta_d d\vec \beta_k \\& = \int p(z_i=k, \vec \theta_d | \vec w_{\neg i},\vec z_{\neg i})p(w_i=t, \vec \beta_k | \vec w_{\neg i},\vec z_{\neg i}) d\vec \theta_d d\vec \beta_k \\& = \int p(z_i=k|\vec \theta_d )p( \vec \theta_d | \vec w_{\neg i},\vec z_{\neg i})p(w_i=t|\vec \beta_k)p(\vec \beta_k | \vec w_{\neg i},\vec z_{\neg i}) d\vec \theta_d d\vec \beta_k \\& = \int p(z_i=k|\vec \theta_d ) Dirichlet(\vec \theta_d | \vec n_{d, \neg i} + \vec \alpha) d\vec \theta_d \\& \times \int p(w_i=t|\vec \beta_k) Dirichlet(\vec \beta_k | \vec n_{k, \neg i} + \vec \eta) d\vec \beta_k \\& = \int \theta_{dk} Dirichlet(\vec \theta_d | \vec n_{d, \neg i} + \vec \alpha) d\vec \theta_d \times\int \beta_{kt} Dirichlet(\vec \beta_k | \vec n_{k, \neg i} + \vec \eta) d\vec \beta_k \\& = E_{Dirichlet(\theta_d)}(\theta_{dk})E_{Dirichlet(\beta_k)}(\beta_{kt})\end{align}
$$
推导得到的最终的条件概率公式如下：
$$
\begin{align} p(z_i=k| \vec w,\vec z_{\neg i}) & \propto E_{Dirichlet(\theta_d)}(\theta_{dk}) \times E_{Dirichlet(\beta_k)}(\beta_{kt}) \\& = \frac{n_{d, \neg i}^{k} + \alpha_k}{\sum\limits_{s=1}^Kn_{d, \neg i}^{s} + \alpha_s} \times \frac{n_{k, \neg i}^{t} + \eta_t}{\sum\limits_{f=1}^Vn_{k, \neg i}^{f} + \eta_f} \end{align}
$$
上述公式是求$d$文档第$i$个词$w_i=t$的主题$z_i$为$k$的条件概率。$n_{d, \neg i}^{k}$是文档$d$中词汇除了$w_i=t$外，属于主题$k$的次数，$\alpha_k$是文档主题$k$的Dirichlet先验参数(伪计数)。$n_{k, \neg i}^{t}$是主题$k$中，除了词汇$w_i$之外，第$t$个词的次数；$\eta_t$是主题词汇$t$的Dirichlet先验参数(伪计数)。Gibbs采样与初始状态无关，因此$\alpha, \eta$合适初始化即可（可能会影响收敛速度）。每次采样更新条件概率后，下一次采样时，$n_{d, \neg i}^{s}$和$n_{k, \neg i}^{f}$都是会变化的，条件概率也都会随之变化，一直到采样稳定。
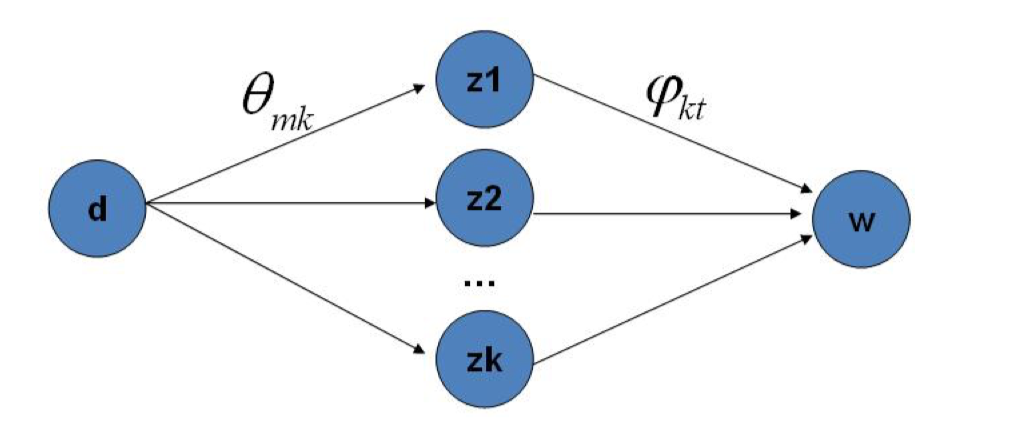
这个公式很漂亮，右边实际上是$p(topic|doc) \times p(word|topic)$，这个概率实际上是$doc \rightarrow topic \rightarrow word$的路径概率，由于Topic有$K$个，所以Gibbs采样的物理意义就是在K条路径中进行采样。
总结下LDA Gibbs采样算法流程。首先是训练流程：
- 选择合适的主题数$K$, 选择合适的超参数向量$\vec{\alpha}、\vec{\eta}$
- 对应语料库中每一篇文档的每一个词，随机的赋予一个主题编号$z$
- 重新扫描语料库，对于每一个词，利用Gibbs采样公式更新它的topic编号，并更新语料库中该词的编号。
- 重复第2步的基于坐标轴轮换的Gibbs采样，直到Gibbs采样收敛。
- 统计语料库中的各个文档各个词的主题，得到文档主题分布$θ_d$，统计语料库中各个主题词的分布，得到LDA的主题与词的分布$β_k$。
下面我们再来看看当新文档出现时，如何统计该文档的主题。此时我们的模型已定，也就是LDA的各个主题的词分布$β_k$已经确定，我们需要得到的是该文档的主题分布。
总结下LDA Gibbs采样算法的预测流程：
- 对应当前文档的每一个词，随机的赋予一个主题编号$z$
- 重新扫描当前文档，对于每一个词，利用Gibbs采样公式更新它的topic编号。
- 重复第2步的基于坐标轴轮换的Gibbs采样，直到Gibbs采样收敛。
- 统计文档中各个词的主题，得到该文档主题分布。
变分推断EM算法
变分推断EM算法希望通过“变分推断(Variational Inference)”和EM算法来得到LDA模型的文档主题分布和主题词分布。首先来看EM算法在这里的使用，我们的模型里面有隐藏变量$θ,β,z$，模型的参数是$α,η$。为了求出模型参数和对应的隐藏变量分布，EM算法需要在E步先求出隐藏变量$θ,β,z$的基于条件概率分布的期望，接着在M步极大化这个期望，得到更新的后验模型参数$α,η$。
问题是在EM算法的$E$步，由于$θ,β,z$的耦合，我们难以求出隐藏变量$θ,β,z$的条件概率分布，也难以求出对应的期望，需要“变分推断“来帮忙，这里所谓的变分推断，也就是在隐藏变量存在耦合的情况下，我们通过变分假设，即假设所有的隐藏变量都是通过各自的独立分布形成的，这样就去掉了隐藏变量之间的耦合关系。我们用各个独立分布形成的变分分布来模拟近似隐藏变量的条件分布，这样就可以顺利的使用EM算法了。
当进行若干轮的E步和M步的迭代更新之后，我们可以得到合适的近似隐藏变量分布$θ,β,z$和模型后验参数$α,η$，进就能够轻易得到我们需要的LDA文档主题分布和主题词汇分布。
要使用EM算法，我们需要求出隐藏变量的条件概率分布如下：
$$
p(\theta,\beta, z | w, \alpha, \eta) = \frac{p(\theta,\beta, z, w| \alpha, \eta)}{p(w|\alpha, \eta)}
$$
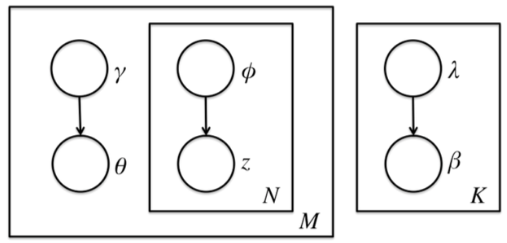
前面讲到由于$θ,β,z$之间的耦合，这个条件概率是没法直接求的，但是如果不求它就不能用EM算法了。我们引入变分推断，具体就是引入基于mean field assumption的变分推断，这个推断假设所有的隐藏变量都是通过各自的独立分布形成的，如下图所示：
将$q(Z)$因子化为:
$$
q(Z)=\prod_{i=1}^{M}q_i(Z_i)
$$
我们假设隐藏变量$θ$是由独立分布$γ$形成的，隐藏变量$z$是由独立分布$ϕ$形成的，隐藏变量$β$是由独立分布$λ$形成的。这样我们得到了三个隐藏变量联合的变分分布$Q$为：
$$
\begin{align} Q(\beta, z, \theta|\lambda,\phi, \gamma) & = \prod_{k=1}^Kq(\beta_k|\lambda_k)\prod_{d=1}^Mq(\theta_d, z_d|\gamma_d,\phi_d) \\& = \prod_{k=1}^Kq(\beta_k|\lambda_k)\prod_{d=1}^M \left(q(\theta_d|\gamma_d)\prod_{n=1}^{N_d}q(z_{dn}| \phi_{dn}) \right) \end{align}
$$
Mean Field对联合分布做了独立性假设，而没有对单个的$q$分布做任何假设(传统EM当中，直接假设隐变量的分布形式，转成参数优化)。这里面存在疑惑的一点是，看网上的资料以PLSA和LDA为例总结EM和变分推断，这里对q的形式是有做假设的，即$q(\beta_k|\lambda_k)$和$q(\theta_d|\gamma_d)$是服从Dirichlet分布，和$q(z_{dn}| \phi_{dn})$服从多项式分布。这几个因子具体分布也有可能是通过平均场理论推导而来的。
我们希望用变分分布$Q$来近似$p(\theta,\beta, z | w, \alpha, \eta) $ , 利用KL散度：
$$
(\lambda^*,\phi^*, \gamma^*) = \underbrace{arg \;min}_{\lambda,\phi, \gamma} KL(Q(\beta, z, \theta|\lambda,\phi, \gamma) || p(\theta,\beta, z | w, \alpha, \eta))
$$
我们的目的就是找到合适的$λ^{∗},ϕ^{∗},γ^{∗}$,然后用$Q(β,z,θ|λ^{∗},ϕ^{∗},γ^{∗})$来近似隐藏变量的条件分布$p(θ,β,z|w,α,η)$，进而使用EM算法迭代。
推导文档的对数似然如下：
$$
\begin{align} log(w|\alpha,\eta) & = log \int\int \sum\limits_z p(\theta,\beta, z, w| \alpha, \eta) d\theta d\beta \\& = log \int\int \sum\limits_z \frac{p(\theta,\beta, z, w| \alpha, \eta) Q(\beta, z, \theta|\lambda,\phi, \gamma)}{Q(\beta, z, \theta|\lambda,\phi, \gamma)}d\theta d\beta \\& = log\;E_Q \frac{p(\theta,\beta, z, w| \alpha, \eta) }{Q(\beta, z, \theta|\lambda,\phi, \gamma)} \\& \geq E_Q\; log\frac{p(\theta,\beta, z, w| \alpha, \eta) }{Q(\beta, z, \theta|\lambda,\phi, \gamma)} \\& = E_Q\; log{p(\theta,\beta, z, w| \alpha, \eta) } - E_Q\; log{Q(\beta, z, \theta|\lambda,\phi, \gamma)} \\& = L(\lambda,\phi, \gamma; \alpha, \eta) \end{align}
$$
上述用到Jense不等式（推导EM的时候也用到过，不再累赘)，这个下界L称为ELBO(Evidence Lower Bound)。为了最大化数据对数似然，我们只需要不断优化下界，使下界不断增大。
换一个角度理解，这个ELBO和我们需要优化的的KL散度关系:
$$
\begin{align} KL(Q(\beta, z, \theta|\lambda,\phi, \gamma) || p(\theta,\beta, z | w, \alpha, \eta)) & = E_Q log Q(\beta, z, \theta|\lambda,\phi, \gamma) - E_Q log p(\theta,\beta, z | w, \alpha, \eta) \\& =E_Q log Q(\beta, z, \theta|\lambda,\phi, \gamma) - E_Q log \frac{p(\theta,\beta, z, w| \alpha, \eta)}{p(w|\alpha, \eta)} \\& = - L(\lambda,\phi, \gamma; \alpha, \eta) + log(w|\alpha,\eta) \end{align}
$$
在上式中，由于对数似然部分和我们的KL散度中要优化的参数无关，可以看做常量，因此我们希望最小化KL散度等价于最大化ELBO。那么我们的变分推断最终等价的转化为要求ELBO的最大值。现在我们开始关注于极大化ELBO并求出极值对应的变分参数$λ,ϕ,γ$。
先将L展开：
$$
\begin{align} L(\lambda,\phi, \gamma; \alpha, \eta) & = E_q[logp(\beta|\eta)] + E_q[logp(z|\theta)] + E_q[logp(\theta|\alpha)] \\& + E_q[logp(w|z, \beta)] - E_q[logq(\beta|\lambda)] \\& - E_q[logq(z|\phi)] - E_q[logq(\theta|\gamma)] \end{align}
$$
上述分解出了7个式子，这7个项可归为2类：狄利克雷分布相对于variational distribution的期望（关于$\beta$和$\theta$的，共4个）、多项分布相对于variational distribution的期望（关于$z$和$w$的，共3个）。
接下来的问题就是极大化ELBO，来求解变分参数$\lambda,\phi,\gamma$。目标是如何把L转成只关于$\lambda,\phi,\gamma$的形式，而不包含$\beta、z、\theta$，利用指数分布族的性质：
$$
p(x|\theta) = h(x) exp(\eta(\theta)*T(x) -A(\theta)) \\
\frac{d}{d \eta(\theta)} A(\theta) = E_{p(x|\theta)}[T(x)]
$$
我们的常见分布比如Gamma分布，Beta分布，Dirichlet分布、多项式分布都是指数分布族。这个性质中，对$T(x)$的期望转成了对$\eta(\theta)$的导数。有了这个性质，意味着我们在ELBO里面一大堆包含$\beta、z、\theta$（服从Dirichlet或多项式分布）的期望表达式可以转化为对目标参数$\lambda、\phi、\gamma$的导数，这样就都约掉了中间变量$\beta、z、\theta$。
最后，对ELBO各个参数求偏导，并令导数为0，就可以得到各个参数在E-step的解析解，3个参数的解析解互相依赖，因此要反复迭代，直到该步稳定。另外，该解析解中包含了实际要求的参数$\alpha, \eta$，这些参数要在M-step计算。在M-step中，对$\alpha, \eta$求导，此时没有解析解，使用梯度下降法或牛顿法迭代求解，直至该步稳定。
E-step:
$$
\begin{align} \phi_{nk} & \propto exp(\sum\limits_{i=1}^Vw_n^i(\Psi(\lambda_{ki}) - \Psi(\sum\limits_{j=1}^V\lambda_{kj}) ) + \Psi(\gamma_{k}) - \Psi(\sum\limits_{h=1}^K\gamma_{h}))\end{align}
$$
$$
\begin{align} \gamma_k & = \alpha_k + \sum\limits_{n=1}^N\phi_{nk} \end{align} $$
$$
\begin{align} \lambda_{ki} & = \eta_i + \sum\limits_{d=1}^M\sum\limits_{n=1}^{N_d}\phi_{dnk}w_{dn}^i \end{align}
$$
M-step:
$$
\begin{align} \alpha_{k+1} = \alpha_k + \frac{\nabla_{\alpha_k}L}{\nabla_{\alpha_k\alpha_j}L} \end{align}
$$
$$
\begin{align} \eta_{i+1} = \eta_i+ \frac{\nabla_{\eta_i}L}{\nabla_{\eta_i\eta_j}L} \end{align}
$$
其中, $\nabla_{\alpha_k}L$,$\nabla_{\alpha_k\alpha_j}L$分别是$\alpha$的一阶导数和二阶导数。$\nabla_{\eta_i}L$和$\nabla_{\eta_i\eta_j}L$分别是$\eta$的一阶导数和二阶导数。
$$
\nabla_{\alpha_k}L = M(\Psi(\sum\limits_{i=1}^K\alpha_{i}) - \Psi(\alpha_{k}) ) + \sum\limits_{d=1}^M(\Psi(\gamma_{dk}) - \Psi(\sum\limits_{j=1}^K\gamma_{dj})) \\\\
\nabla_{\alpha_k\alpha_j}L = M(\Psi^{\prime}(\sum\limits_{i=1}^K\alpha_{i})- \delta(k,j)\Psi^{\prime}(\alpha_{k}) ) \\\\
\nabla_{\eta_i}L = K(\Psi(\sum\limits_{j=1}^V\eta_{j}) - \Psi(\eta_{i}) ) + \sum\limits_{k=1}^K(\Psi(\lambda_{ki}) - \Psi(\sum\limits_{j=1}^V\lambda_{kj})) \\\\
\nabla_{\eta_i\eta_j}L = K(\Psi^{\prime}(\sum\limits_{h=1}^V\eta_{h}) - \delta(i,j)\Psi^{\prime}(\eta_{i}) )
$$
其中，当且仅当$i=j$时，$δ(i,j)=1$,否则$δ(i,j)=0$。
总结该算法步骤：
输入：主题数$K$,$M$个文档与对应的词。
1） 初始化$α,η$向量。
2）开始EM算法迭代循环直到收敛。
a) 初始化所有的$ϕ,γ,λ$，进行LDA的E步迭代循环,直到$λ,ϕ,γ$收敛。
(i) for $d$ from 1 to $M$:
for $n$ from 1 to $N_d$:
for $k$ from 1 to $K$:
更新$ϕ_{nk}$。
标准化$ϕ_{nk}$使该向量各项的和为1。
更新$γ_k$。
(ii) for $k$ from $1$ to $K$:
for $i$ from 1 to $V$:
更新$λ_{ki}$。
(iii)如果$ϕ,γ,λ$均已收敛，则跳出a)步，否则回到(i)步。
b) 进行LDA的M步迭代循环， 直到$α,η$收敛。
(i) 用牛顿法迭代更新$α,η$直到收敛。
c) 如果所有的参数均收敛，则算法结束，否则回到第2)步。
算法结束后，我们可以得到模型的后验参数$α,η$以及我们需要的近似模型主题词汇分布$λ$, 以及近似训练文档主题分布$γ$。
$\lambda_{ki}$是语料层面的参数，每遍历一遍全量的训练文档只需要更新一次；$\gamma_{k}$ 和 $\phi_{nk}$ 是文档层面的参数，每“见到”一篇文档都会对该文档对应的参数进行优化。
若是要对一篇新文档的主题分布作推断，只需要执行 $\gamma_{k}$ 和 $\phi_{nk}$的更新部分。
上述只是一种极大化ELBO的方法，还有其他方法可以参见变分推断与LDA。
引用
LDA数学八卦
