本文是对论文《Collaborative Topic Modeling for Recommending Scientific Articles》的读书报告。这是一篇发表在KDD2011上的论文,目前引用量874次,是推荐系统领域较权威的一篇文章。
背景
这篇文章的研究目的是希望为科研工作者快速找到其感兴趣的相关论文。人工的方法通常是通过某一篇论文的引用来找到其他论文。这种方法很有效,但是太局限。举个例子,统计学家可能会错过在其他学科,如经济学、生物学上面的一些相关文章,因为跨学科很少互相引用。另外,还可以通过关键字查找,这种方法同样有局限,例如你可能描述不清要查找的文章,查找也只能依赖于文字内容。
目前,有些网站(在线社区),例如CiteULike 和 Mendeley允许研究者创建自己感兴趣的引用库,并和他人分享。这使得利用推荐系统为研究者推荐文章成为了可能。在这篇文章中,作者利用CiteULike提供的数据集,每一个用户有一个自己感兴趣的文章列表,目标是研究一种推荐算法,来给每个用户推荐其列表中不存在的、且可能感兴趣的文章。
作者认为该推荐算法有几个重要的点。
- 首先是能够推荐旧的文章,研究者倾向于阅读旧的、奠基性的文章来发现新领域或加深对某个领域的理解。因此在推荐旧文章时,其他用户的意见起着重要的作用,一个奠基性的文章会出现在很多人的文章列表中,而不重要的文章就很少出现在他人的列表中。
- 其次,要能够推荐新的文章,研究者会追踪当下最流行的方法的新进展。由于是新文章,应该很少会出现在用户的列表中,传统的协同过滤方法无法做出推荐,对于新文章的推荐,推荐算法必须要利用该文章的内容。
- 最后就是模型的解释性。作者希望有一些探索性的因素能够提升这种在线社区的影响力。例如,我们希望能够基于用户喜欢的文章的内容,总结出每个用户的偏好和画像,使得相似用户可以联系在一起,并给出解释。例如,我们还可以使用“哪种类型的用户喜欢该文章”的方式来描述文章。举个例子,“某篇机器学习文章深受计算机视觉研究者的喜好“。
相关工作
文章提出的方法结合了基于隐因子的协同过滤矩阵分解算法和基于概率主题模型的内容分析算法。协同过滤算法能够利用他人的文章库推荐旧文章,对于新文章,可以使用主题模型来推荐,该模型能够推荐和用户喜欢的文章的内容相似的新文章。
矩阵分解:Recommendation by Matrix Factorization
在矩阵分解中,我们使用同一个低维的隐语义空间来表示用户和物品。用户使用隐向量$u_i \in \mathbb{R}^K$, 物品使用隐向量$v_j \in \mathbb{R}^K$。预测用户是否对某个物品感兴趣,使用二者的点积。
$$
\hat{r}_{ij}=u_i^T v_j
$$
通过最小化预测值和观测值的平方误差来优化。
$$
min_{U,V} \sum_{i,j}(r_{ij}-u_i^Tv_j)^2 + \lambda_u ||u_i||^2 +\lambda_v ||v_j||^2
$$
其中,$U=(u_i)_{i=1}^I, V=(v_j)_{j=1}^J$
该形式的矩阵分解可以拓展成概率矩阵分解(PMF)。PMF的核心假设是,观测噪声($r_{ij}-u_i^Tv_j$)服从高斯分布$N(0, c_{ij}^{-1})$, 则$r_{ij} \sim N(u_i^Tv_j, c_{ij}^{-1})$。另外,$u, v$服从高斯分布(相当于正则化项,MF中也有)。PMF认为数据生成过程如下:
1) 对每个用户$i$, 根据高斯分布抽取用户隐向量, $u_i \sim N(0, \lambda_u^{-1}I_k)$, $\sigma_u^2=\lambda_u^{-1}$
2) 对每个物品$j$,根据高斯分布抽取物品隐向量,$v_j \sim N(0, \lambda_v^{-1}I_k)$, $\sigma_v^2=\lambda_v^{-1}$
3)对每个用户-物品交互数据$(i,j)$,根据高斯分布抽取值:$r_{ij} \sim N(u_i^T v_j, c_{ij}^{-1})$。$\sigma^2=c_{ij}$可以看做是$r_{ij}$的精度参数,或置信度参数。
为了优化PMF,我们使用MAP最大后验概率估计,计算参数$u,v$。因此计算$u,v$的后验概率:
$$
P(u,v,|r,\sigma^2,\sigma_U^2,\sigma_V^2)=P(r|u,v,\sigma^2)P(u|\sigma_u^2)P(v|\sigma_v^2)
$$
代入高斯密度函数并取对数,即可得到对数似然代价函数如下:
$$
E =\sum_{i=1}^I \sum_{j=1}^J \frac{c_{ij}}{2} (r_{ij}-u_i^Tv_j)^2 + \frac{\lambda_u}{2}\sum_{i=1}^I ||u_i||_F^2 + \frac{\lambda_v}{2}\sum_{j=1}^J ||v_j||_F^2
$$
$$
\lambda_u=\frac{1}{\sigma_u^2} , \lambda_v=\frac{1}{\sigma_v^2}, c_{ij}=\frac{1}{\sigma^2}
$$
实际上,当$c_{ij}=1$时(置信度100%,数据不存在噪声),上述PMF损失和MF损失一致。因此PMF和MF的差别仅在$c_{ij}$,$c_{ij}$越大,$r_{ij}$置信度越高。在本文中,认为用户文章库中的的数据置信度高,即$r_{ij}=1$的数据置信度高;相反,$r_{ij}=0$的数据既可以解释成用户不感兴趣,也可以解释成用户没看到过该文章。这和one-class协同过滤问题一样,作者使用相同的策略来设置$c_{ij}$: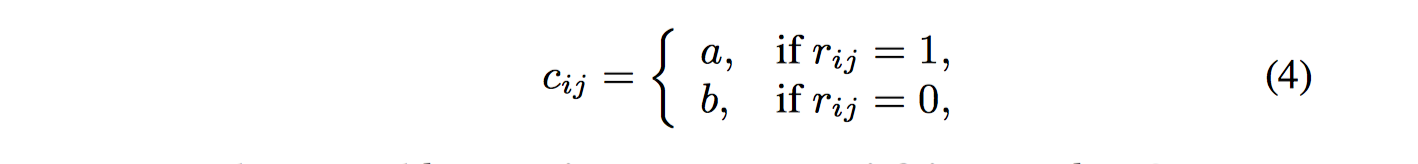
其中,$a,b$是超参数,通过调参来满足$a>b>0$
矩阵分解的缺点在于,可解释性差;无法推广到新物品的推荐。
概率主题模型
概率主题模型用于发现一组文档集合的主题,该主题使用在词汇上的分布来表示。主题模型能够提供文档低维表示的可解释性。广泛应用于预料发现、文档分类和信息抽取。
使用最广泛的主题模型是LDA(Latent Dirichlet Allocation)。LDA认为文档中的每个词是通过主题生成的。这里面涉及两种分布,文档主题分布和主题词汇分布。
在生成一篇文章$w_j$时,
1)首先需要确定该文档的主题分布。LDA假设其服从Dirichlet分布。$\theta_j \sim Dirichlet(\alpha)$
2) 对文档中的第$n$个词:
a) 首先根据该文档的主题分布抽取具体的主题对应的编号。$z_{jn} \sim Mult(\theta_j)$
b) 再根据该主题对应的词汇分布$\beta_{z_{jn}}$来抽取具体词汇。$w_{jn} \sim Mult(\beta_{z_{jn}})$
其中,每篇文档的主题分布是各自独立的,$M$篇文档就有$M$个文档主题分布; 而主题的词汇分布是所有文档共享的,假设有$K$个主题,则主题的词汇分布就有$K$个。
LDA模型通过最大化语料数据的对数似然来优化,需要使用变分EM算法来学习。对于新文档,可以使用变分推断来确定其主题分布。作者的目标是使用主题模型为文章构建基于内容的表示(主题表示)。
主要思想
作者提出的算法利用到了2种类型的数据,用户感兴趣的文章库和文章的内容。对每个用户,该算法既可以发现对于其他相似用户来说很重要的旧文章,也可以发现能够反映用户特定兴趣的新的文章。最后,该算法还能够对用户或文章的表示形式,给出很好的解释。
作者将这两种方法统一到一个概率模型中,且模型会权衡文章内容和他人文章库的重要性,一篇很少被人收藏的文章更多依赖于其内容,而一篇被广泛收藏的文章更多依赖于他人协同。
一种融合两种思想的方法是,直接将矩阵分解中要学习的文章隐向量替换成LDA中的文章主题向量。
$$
r_{ij} \sim N(u_i^T \theta_j, c_{ij}^{-1})
$$
这个模型的问题是难以区分开 对于推荐系统解释性好的主题 与 对于文本内容重要的主题。举个例子,考虑到两篇文章A和B,都是关于机器学习应用于社交网络,二者相似,因此文档主题分布$\theta_A、\theta_B$很相近。进一步,如果这两篇文章对不同类型的研究者吸引力不同,A重点讲机器学习算法本身,社交网络上的应用只是简单的举个例子,而B重点关注如何利用机器学习算法对社交网络上的数据进行分析。显然,对于机器学习研究者,更喜欢A,对于社交网络研究者更喜欢B。
这种差异不能通过LDA主题建模来发现,但可以利用用户和文章的交互数据来发现。为了利用交互数据建模出这种差异,可以添加主题的隐偏移$\epsilon_j$。交互数据越多,$\epsilon_j$计算越准确。这个偏移值可以解释,为什么文章A对机器学习研究者更受欢迎一些,文章B对社交网络研究者更受欢迎一些。同时,还能解释模型的预测更依赖于文章的文本内容,还是更依赖于他人的数据($\epsilon$越大,说明更依赖于后者;越小,说明更依赖于前者)。
本文提出的协同主题回归CTR具体生成数据的过程如下:
1) 对每个用户$i$, 根据高斯分布抽取用户隐向量, $u_i \sim N(0, \lambda_u^{-1}I_k)$, $\sigma_u^2=\lambda_u^{-1}$
2) 对每个物品$j$,
a) 抽取物品的主题分布,$\theta_j \sim Dirichlet(\alpha)$
b) 抽取物品的隐偏移量,$\epsilon_j \sim N(0, \lambda_v^{-1}I_k)$,并令物品的隐向量为:$v_j=\epsilon_j+\theta_j$
c) 对每一个词汇$w_{jn}$,
i. 首先根据该文档的主题分布抽取具体的主题对应的编号。$z_{jn} \sim Mult(\theta_j)$
ii. 再根据该主题对应的词汇分布$\beta_{z_{jn}}$来抽取具体词汇。$w_{jn} \sim Mult(\beta_{z_{jn}})$
3)对每个用户-物品交互数据$(i,j)$,根据高斯分布抽取值:$r_{ij} \sim N(u_i^T v_j, c_{ij}^{-1})$。
CTR的核心在于物品隐向量$v_j$的构建$v_j=\epsilon_j+\theta_j$。注意到,$\epsilon_j \sim N(0, \lambda_v^{-1}I_k)$和PMF中的$v_j \sim N(0, \lambda_v^{-1}I_k)$是一样的。这意味着,我们假设物品的隐向量$v_j$很接近物品的主题向量$\theta_j$, 但是可能会偏移$\theta_j$, 偏移的程度取决于交互数据。 $r_{ij}$的期望如下:
$$
\mathbb{E}[r_{ij}|u_i,\theta_j,\epsilon_j]=u_i^T(\theta_j+\epsilon_j)
$$
$r_{ij}$是关于$\theta_j$的线性函数,故称此模型为协同主题回归。
CTR模型的架构如下图:
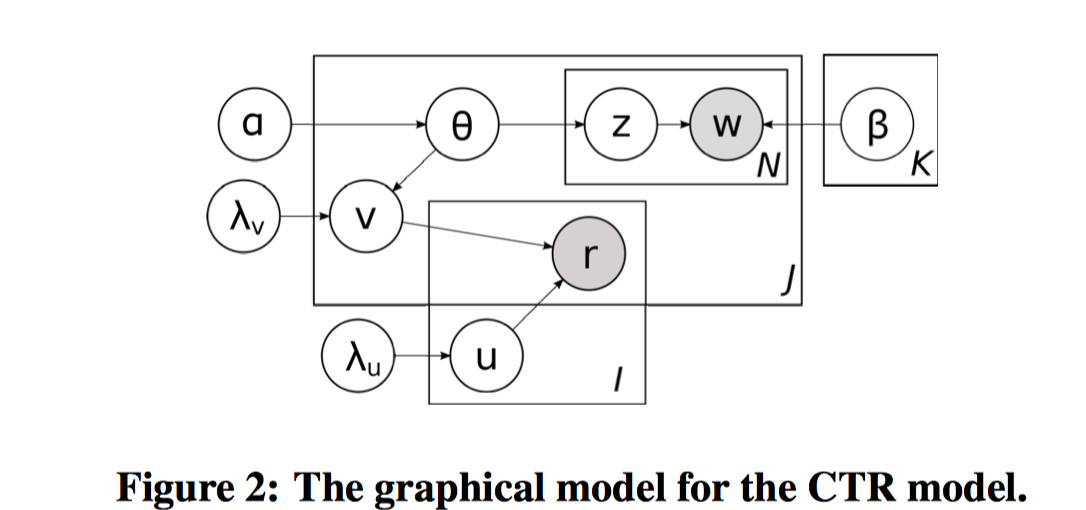
阴影部分代表可观测的数据,方框以外是超参数,方框以内白色的圆圈是要学习的隐变量参数,参数分成3个部分,用户相关的,物品相关的,主题相关的。
参数的学习
作者假定文档主题分布的Dirichlet先验分布参数固定,为$\alpha=1$。对于LDA模型,我们最主要要学习的参数是主题词汇分布参数$\beta_k$和文档主题分布$\theta_j$。对于PMF模型,我们要学习的参数包括:$u_i,v_j$。
对于给定的主题词汇分布参数$\beta_k$, 直接求参数$u_i,v_j,\theta_j$的贝叶斯估计是难以做到的。采样EM算法来学进行大化后验估计。E-step固定$\beta_k$更新$u_i,v_j,\theta_j$, M-step最大化$\beta_k$。在给定$\lambda_u,\lambda_v,\beta_k$下, 参数$u_i,v_j,\theta_j, R$的完全对数似然如下:
$$
L =-\sum_{i,j} \frac{c_{ij}}{2}(r_{ij}-u_i^Tv_j)^2 -\frac{\lambda_u}{2}\sum_{i=1}^I ||u_i||_F^2 - \frac{\lambda_v}{2}\sum_{j=1}^J ||v_j-\theta_j||_F^2 + \sum_j \sum_n log(\sum_k\theta_{jk}\beta_{k, w_{jn}})\tag{1}
$$
第一项是根据$r_{ij}$服从高斯分布得到,第二项是根据$u_i$服从高斯分布得到,第三项是根据$v_j$服从的高斯分布(可以得出,$v_j \sim N(\theta_j, \lambda_v^{-1}I_k)$ )得到。最后一项是根据,文档-主题, 主题-词汇的联合概率计算得到。
值得注意的是,主题模型和概率矩阵分解模型是在一个统一的框架下共同学习的,并且同时利用文本数据和评分数据进行优化。(不过在该数据集中,作者也有直接固定使用单独LDA得到的$\theta_j$,得到的模型性能也不错,还节省了计算)
对于参数$u_i,v_j$的优化,直接根据$L$对其导数,并令导数为0,即可得到:
$$
u_i \leftarrow (VC_iV^T+\lambda_uI_k)^{-1}VC_iR_i \tag{2}
$$
$$
v_j \leftarrow (UC_jU^T+\lambda_vI_k)^{-1}(UC_jR_j+\lambda_v\theta_j) \tag{3}
$$
其中,$U=(u_i)_{i=1}^I, V=(v_j)_{j=1}^J$, $C_i$是对角矩阵,对角元素为$c_{ij}$, $j=1,…,J$。$R_i=(r_{ij})_{j=1}^J$为用户$i$的文章库。上述公式展示了$\theta_j$如何影响$v_j$,$\lambda_v$权衡了这种影响程度。上述计算的复杂度和用户文章库的文章数量呈线性关系。
接下来是$\theta_j$的学习。先定义$q(z_{jn}=k)=\phi_{jnk}$,即文档$j$中第$n$个词语所属的主题为$k$的概率(和$\beta_{k,w_{jn}}$含义一样),作为隐变量引入。将对数似然函数中包含$\theta_j$分离出来,并使用Jensen不等式:
$$
\begin{align} L(\theta_j) & = - \frac{\lambda_v}{2} ||v_j-\theta_j||_F^2 + \sum_n log(\sum_k\theta_{jk}\beta_{k, w_{jn}}) \\& = - \frac{\lambda_v}{2}||v_j-\theta_j||_F^2 + \sum_n log(\sum_k \frac{\theta_{jk}\beta_{k, w_{jn}} \phi_{jnk} }{\phi_{jnk}} ) \\& \geq - \frac{\lambda_v}{2}||v_j-\theta_j||_F^2+\sum_n \sum_k\phi_{jnk}( log \theta_{jk}, \beta_{k,w_{jn}}-log \phi_{jnk}) \\& = L(\theta_j, \phi_{j})\end{align} \tag{4}
$$
$\phi_j=(\phi_{jnk})_{n=1,k=1}^{N \times K}$。得到$\phi_{jnk}$的估计,
$$
\phi_{jnk} \propto \theta_{jk}\beta_{k,w_{jn}}
$$
接着,对上述$L(\theta_j,\phi_j)$求$\theta_j$的导数,并令导数为0,得到$\theta_j$的更新公式(论文没有给出具体式子,并且指出需要使用投影梯度来优化)。
最后,在M-step优化$\beta_{kw}\propto \sum_j\sum_n \phi_{jnk} I[w_{jn}=w]$。
预测
CTR能够同时预测旧数据和新数据。令$D$为观测数据,预测公式如下:
$$
\mathbb{E}[r_{ij}|D]\approx \mathbb{E}[u_i|D]^T(\mathbb{E}[\theta_j|D]+\mathbb{E}[\epsilon_j|D])
$$
对于旧数据的预测(In-matrix prediction),使用$u_i,\theta_j,\epsilon_j$的点估计来近似期望。
$$
r_{ij}^{*} \approx (u_i^{*})^T(\theta_j^{*}+\epsilon_j^{*})=(u_i^{*})^Tv_j^{*} \tag{5}
$$
对于新数据的预测(out-matrix prediction),由于没有任何观测数据,因此$\mathbb{E}[\epsilon_j|D]=0$,则:
$$
r_{ij}^{*} \approx (u_i^{*})^T \theta_j^{*} \tag{6}
$$
为了获取一篇新文章的主题分布$\theta_j^{*}$,只需要根据上述公式4(第一项不需要),迭代优化参数$\theta_j^{*}$。
实验
本次实验将使用CTR模型来分析CiteULike数据集。
数据
隐式反馈数据集CiteULike。作者对原始数据进行了处理。通过合并重复文章,移除空文章,移除文章库少于10篇的用户,最终得到 5551用户, 16980文章 以及 204986条交互数据(user-item),这个交互数据矩阵的稀疏性达到了$99.8\%$,平均1个用户的文章库是37篇,范围从10~403,93%的用户文章库数量少于100篇。另外,对每篇文章,只使用文章的标题和摘要,作者去除了停用词,使用tf-idf抽取了最高的8000个不同的词作为词典。
指标
实验使用的评估指标是召回率。对每个用户,会按照预测的评分推荐TopM篇文章(训练集之外的TopM篇文章)。然后在验证集上,看TopM篇文章,哪些真正出现在用户的文章库中。作者之所以只采用召回率,是考虑到评分为0的文章,既可能是用户看过这篇文章但是不喜欢,也可能是用户不知道这篇文章。而评分为1的文章一定是用户喜欢的。因此作者只关注评分为1的文章。M越小,而Recall值越大,说明推荐算法越强。对每个用户,定义Recall@M:
$$
Recall@M=\frac{number\ of \ articles \ the \ user \ likes \ in \ top M }{\ total \ number \ of \ article \ the \ user \ likes }
$$
最终整个模型的recall,需要对所有用户的recall值取平均。
上述评估指标是面向用户的,也可以使用面向文章的指标。对于某篇文章,对比一下模型预测哪些用户会对这篇文章感兴趣,以及这篇文章实际出现在哪些用户的文章库中,计算推荐的Recall。
下面会对新文章(out-of-matrix prediction)和旧文章(in-matrix prediction进行预测和推荐评估。
数据划分
In-matrix prediction
In-matrix prediction是指预测某个用户喜欢看的文章时,这个用户未曾看过的文章(要预测的文章)至少出现在其他一个用户的文章库中。
为了验证这种推荐的性能。我们将数据集划分成训练集和测试集,并保证测试集中的文章都出现在训练集中。
使用5折交叉验证。对至少出现在5个用户的文章库中的文章,按照文章来层次划分,保证每折当中都出现该文章。而对于出现次数少于5次的文章,全部放到训练集中,这样能保证测试集中的文章,全都出现在训练集中。5次评估,每次在其中4折上训练,在另外1折上预测。但是要注意,每个用户在那一折上预测时,测试的文章列表(用户未曾观看的)都不一样。具体处理时,首先得到测试集上的所有文章,然后对某一个用户,过滤出这些文章中哪些未出现在训练数据中该用户的文章库里,得到过滤的文章(该用户未曾看过的文章)后,预测用户对这些文章哪些感兴趣,得到TopM,然后再和测试集上用户真正感兴趣的文章进行对比,求recall。
out-of-matrix prediction
out-of-matrix prediction是指预测某个用户喜欢看的文章时,这个用户未曾看过的文章(要预测的文章)未出现在任何一个用户的文章库中。同样对文章划分成5折。每次对1折进行测试,对其余4折进行训练时,会从其余4折中剔除在1折中出现的文章数据,对4折中剩余的数据进行训练,再在1折上的所有文章进行测试,此时对所有用户而言,测试文章列表都一样(1折上的所有文章),并在1折上进行评估。
对比实验
对比的模型包括CF、LDA、CTR。
首先是参数的设定:
通过Grid Search进行超参数设定。CF参数:$K=200,\lambda_u=\lambda_v=0.01,a=1,b=0.01$。
除了$\lambda_v$,CTR参数和CF基本一样。参数$\lambda_v$考察了物品的隐向量$v_j$偏离主题向量$\theta_j$的程度。因此进一步考察$v_j$取值的影响,$\lambda_v \in {10,100,1000,10000}$。$\lambda_v$越大,代表对$v_j$偏离主题向量$\theta_j$的惩罚越大,则学习到的二者差距越小,即越依靠LDA模型。
另外对于LDA,等价于在CTR中固定$v_j = \theta_j$,即物品隐向量只和文本内容有关,而$u_i$的学习使用的是评分数据。CTR模型中$\beta、\theta$参数的初始化会使用LDA的结果进行初始化。
最后,baseline使用随机推荐模型,一个用户看了M篇随机文章,则推荐的recall期望值和M篇的占比有关,$M/M_{tot}$。
- 模型对比实验
对比时,CTR的$\lambda_v=100$。下图考察了M=20,40,…,200时CF、LDA、CTR的召回率。
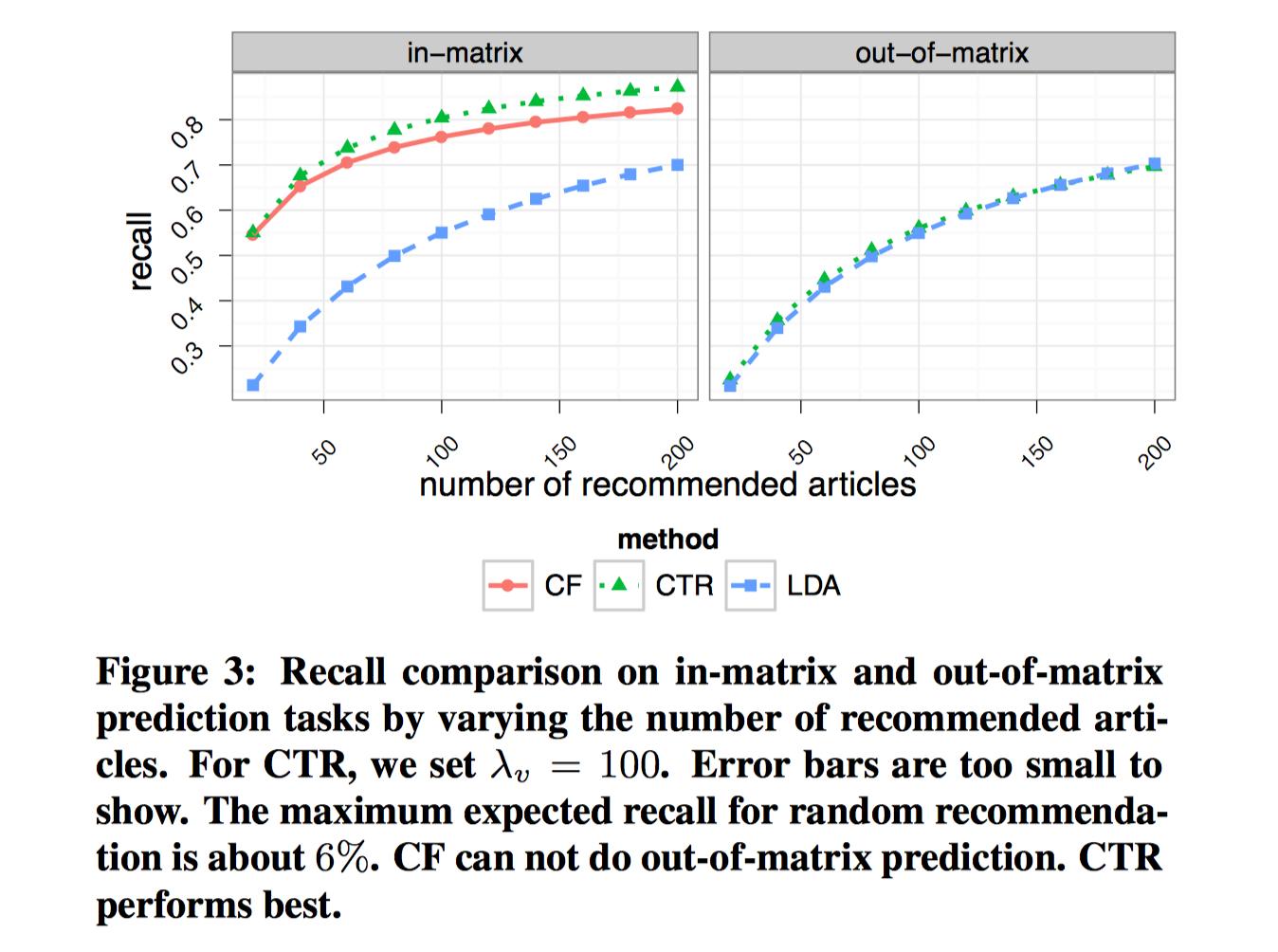
左图是in-matrix-prediction,3个模型都能够预测,可以看到CTR模型最佳,CF其次,LDA最后。CF和LDA的差距表明了评分数据的有效性,LDA性能差,也是因为没有考虑评分数据对物品隐向量$v_j$的调整作用。
右图是out-of-matrix prediction,只能使用CTR和LDA,可以看到二者性能相近,CTR略微好一点。原因是此时二者学习到的用户隐向量一致,学习到的物品隐向量只和文本内容有关,二者也一样。
参数对比实验
对于CTR模型,固定M=100,考察$\lambda_v$不同取值的影响。
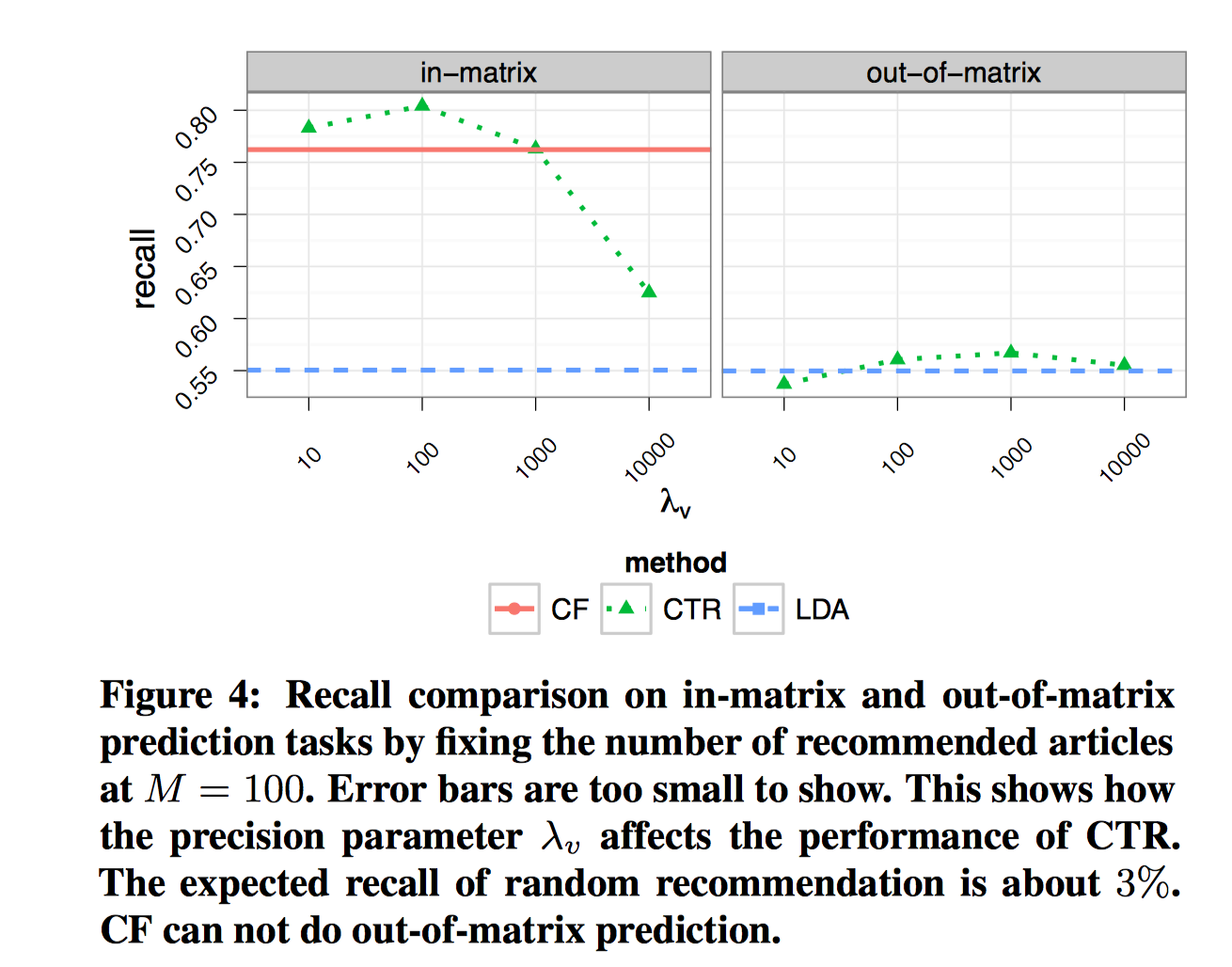
$\lambda_v$越小,则$v_j$偏离$\theta_j$的程度越大,此时CTR类似CF,主要依赖于评分数据,基本上依靠文本内容计算$\theta_j$的似然项不起多大作用;$\lambda_v$越大,此时模型会依赖于文本内容,使得$v_j$不会偏离$\theta_j$太大。当$\lambda_v$无穷大时,$v_j=\theta_j$,此时CTR退化成LDA。从图中可以看出,$\lambda_v=100$时,CTR最优。
作者最后还考察了,用户文章库中文章的数量对模型的影响,以及一篇文章出现在文章库中的次数对模型的影响。对于前者,对每个用户,作者画出了其拥有的文章数量,模型的recall值对比情况;对于后者,对每篇文章,作者画出了其出现在文章库中的次数,模型的recall值。
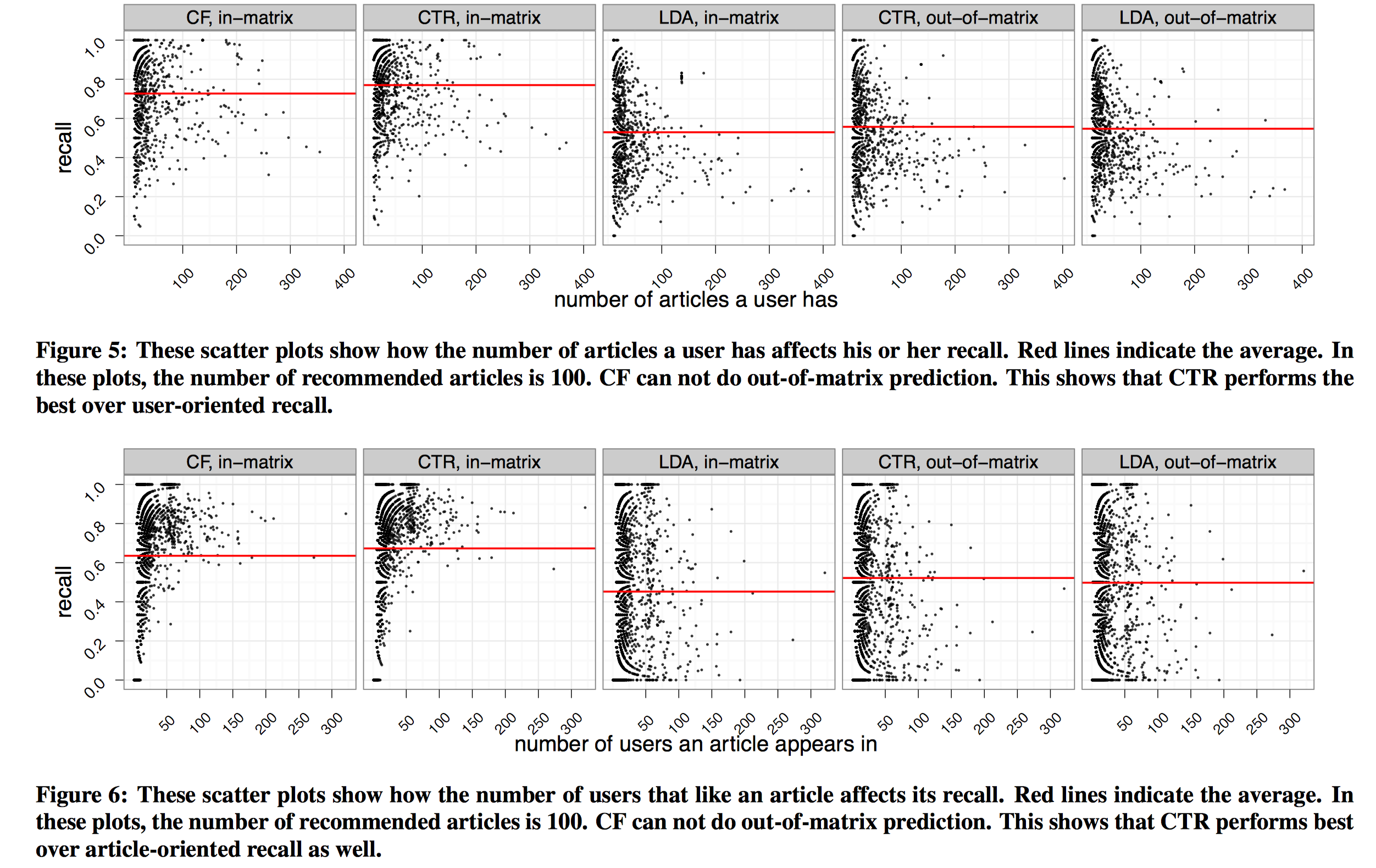
根据上图,用户的文章库越多,则预测的方差越小(竖直看recall方差),用户的文章库数量越少,预测的方差越大。并且随着文章数量的增加,越难预测准确,这和直觉是一样的,一个用户阅读越多,越可能阅读到一些冷门的文章,较少的出现在其他人的文章库中,而这些文章很难预测准。在上图的下方,可以看出一个文章的数量出现在不同用户的文章库中的次数越多,recall值越稳定、越高。因为这些文章有更多的协同信息。
CTR模型探索性分析
用户画像
CTR模型的一个好处是能够利用LDA主题模型学习到的主题来解释用户隐空间。对于一个用户,隐向量$u_i$的每个分量实际上衡量了该用户对不同主题的感兴趣程度,可以对所有的分量进行排序,并取出TopK个值最大的分量对应的TopK个主题,每个主题用其在词语上的分布来描述($\beta$),选出表征该主题的权重值最大的若干个词,作为用户的画像标签。下表展示了两个用户的Top3主题,同时展示了CTR模型预测的用户感兴趣的Top10篇文章。
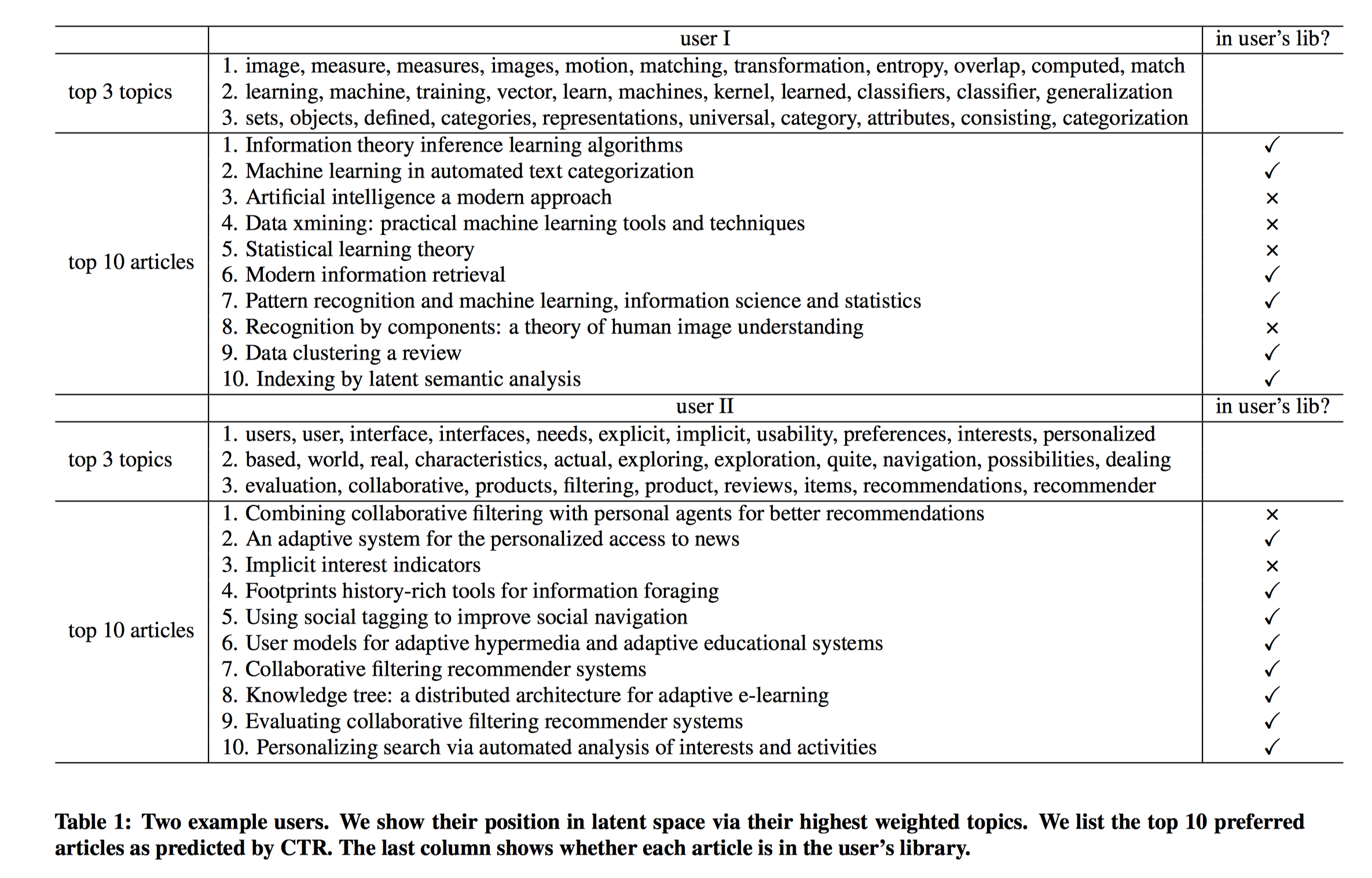
可以推测,用户1可能是文本或图像领域的机器学习研究者;用户2可能是用户交互设计、推荐领域的研究者。
文章隐空间
我们观察不同文章的$\epsilon_j$值。下表展示了$\epsilon_j$值最大($\epsilon_j^T\epsilon_j=(v_j-\theta_j)^T(v_j-\theta_j)$)的Top10篇文章。 第二列、第三列分别是出现在数据集中的次数以及谷歌学术上的引用次数,可以看出这些$\epsilon_j$值大的文章都是热门、流行的好文章,很多用户都感兴趣的,有着很广泛多样的阅读群体,因此蕴含着丰富的协同信息,使得模型学习时,最终的文章隐向量$v_j$偏离文章的主题向量$\theta_j$越多。最后两列显示了有这些文章的用户的平均预测Recall和没有这些文章的平均预测Recall,可以看出有这些文章的用户的平均预测Recall高很多。
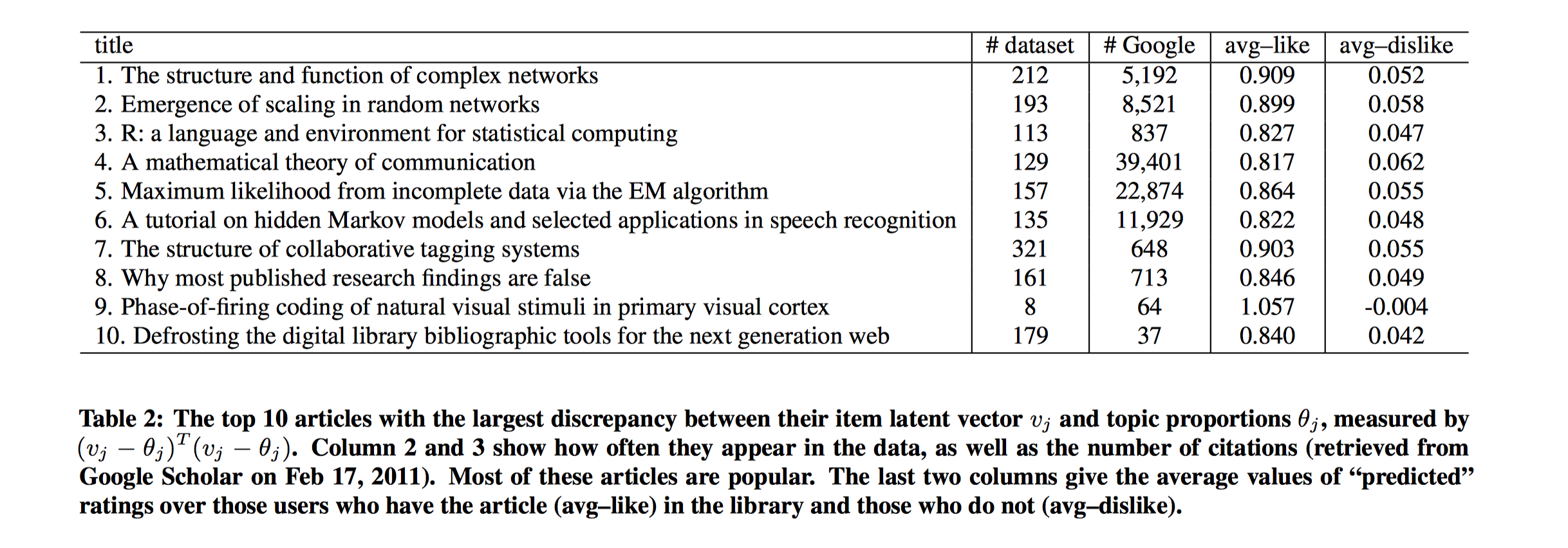
另外,作者还单独观察了$\epsilon_j$中分量$\epsilon_{jk}$最大的下标$k$, 和$\theta_j$中分量$\theta_{jk}$最大的下标$k^{\prime}$的关系。如下图:
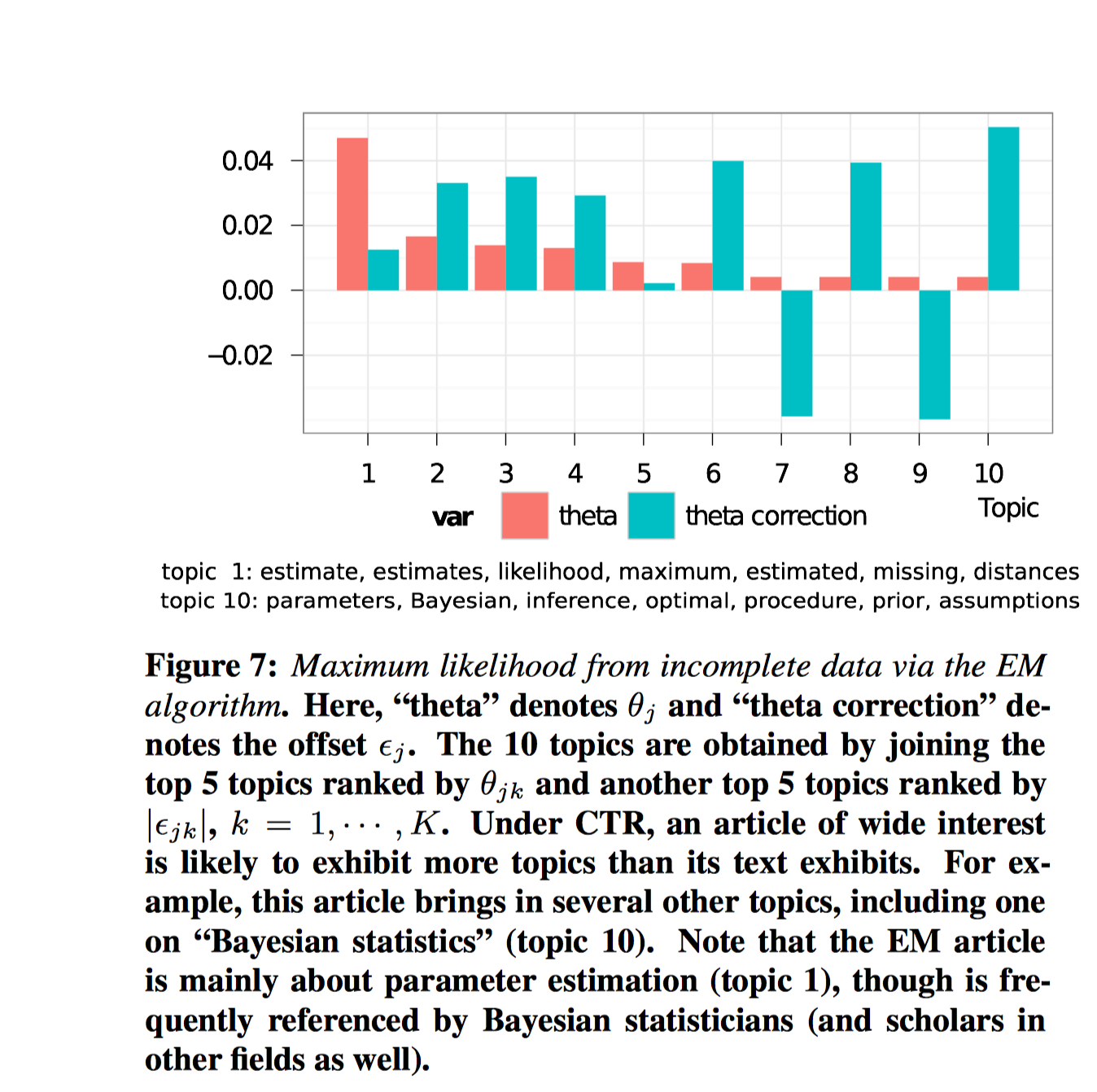
对这篇文章《Maximum likelihood from incomplete data via the EM algorithm》来说,Topic$\theta_j$分量最大的主题是Topic1,而偏移$\epsilon_j$最大的主题是Top10。Topic1说明这篇文章主要是关于参数估计。Topic10是关于贝叶斯统计,这篇文章本来不是关于贝叶斯统计的,但是却体现出贝叶斯统计,这是由协同数据造成的,说明贝叶斯统计的研究者会经常引用这篇参数估计的文章。
作者针对这点又举了另一个例子:
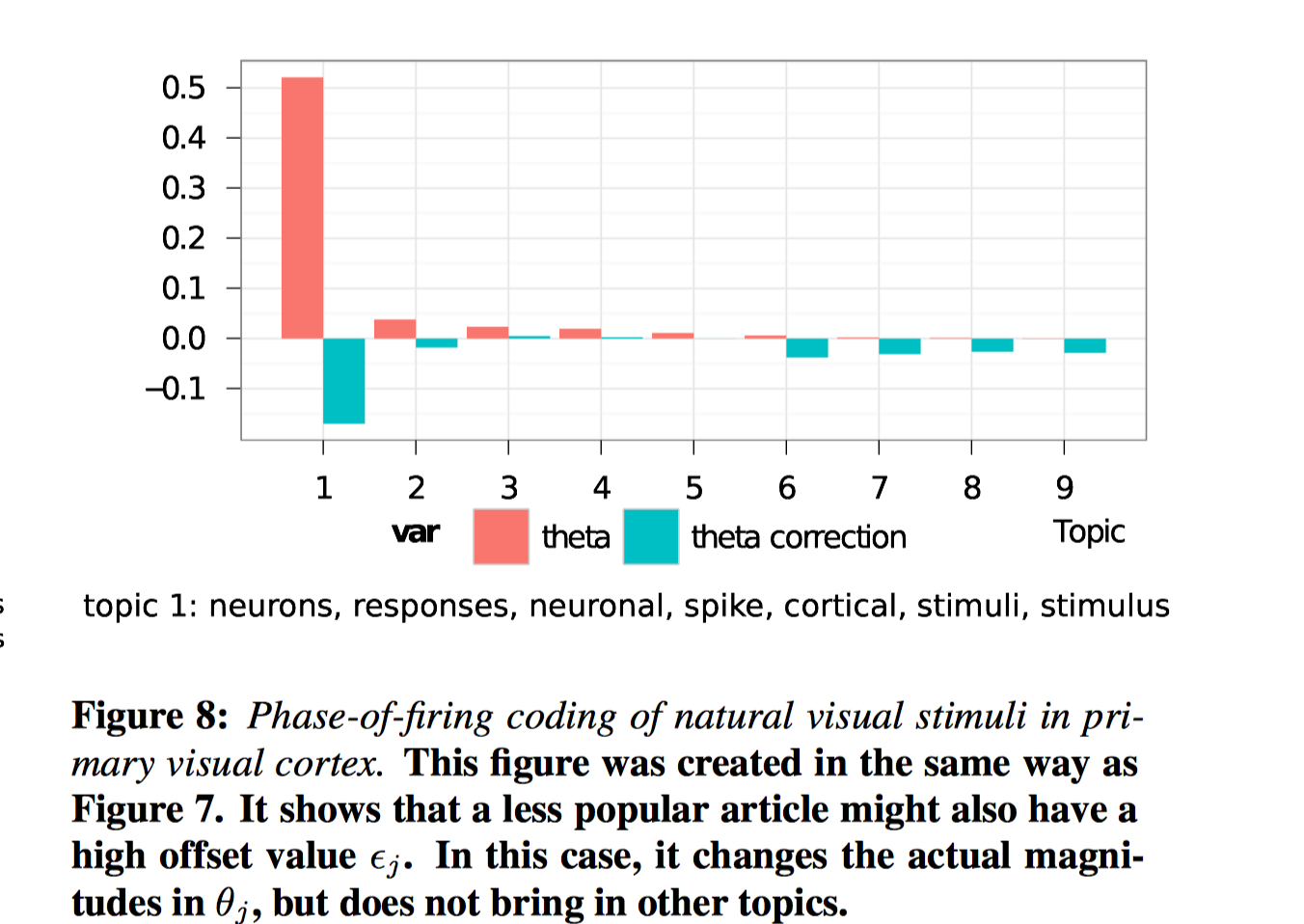
这篇是关于计算神经学的文章。Topic和offset最大的都是Topic1, 说明这篇文章对研究领域不是神经学的其他研究者来说不具备很强的吸引力。offset的作用仅在于优化目标函数,而没有带来其他的主题。
总结
这篇文章提出了一种新的推荐算法CTR,结合了基于内容的推荐和基于评分数据的推荐。实验表明,CTR性能比传统的CF要好。同时,CTR模型能够提供非常好的解释性,能够为用户建立画像标签,这对推荐系统而言是非常重要的,例如:一个用户知道了自己的用户画像后,可以选择隐藏掉某些主题,来避免这些主题内容的推荐。
参考
Collaborative Topic Modeling for Recommending Scientific Articles

