变分推断示例
本报告是论文《Scalable Recommendation with Poisson Factorization》变分推断的推导过程。
回顾
一般变分推断前,需要先看看通过后验估计能不能优化参数。正常步骤是先计算所有隐变量的后验概率,然后对后验概率取对数,看看对数形式的目标函数能不能通过简单的梯度下降等方式进行优化。但是,大部分情况下,后验概率形式很复杂,很难计算。其中一个原因是,后验概率的分母是关于样本的边缘概率密度,需要对隐变量积分,通常该积分很难计算,无法得到闭合解。因此需要使用近似推断。变分推断的目的是使用简单的分布来拟合复杂的分布(即隐变量的后验概率分布)。通过优化KL散度(等价于最大化ELBO)来求解该简单分布。
概率模型
《Scalable Recommendation with Poisson Factorization》论文中的概率图模型如下。
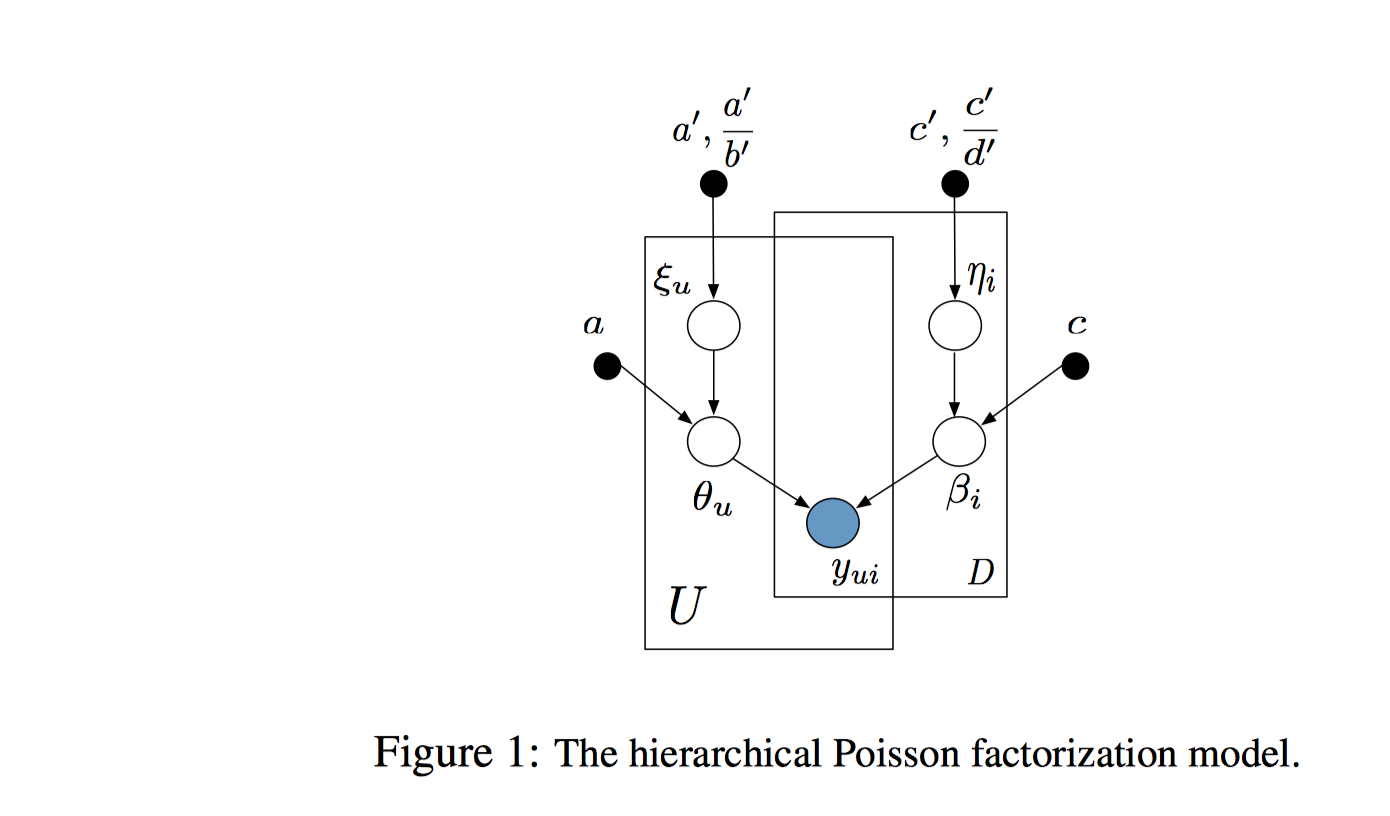
数据生成过程如下:

先给出最终的优化方法。使用coordinate ascent优化如下:

下面会推导上述的优化迭代公式。
基础知识
这部分将直接使用如下结论,可以参考徐老师的课件。
ELBO
elbo是我们要优化的目标,我们希望最大化该目标。

指数分布族性质
$$
p(x|\theta) = h(x)exp \left( T(x)^T \eta(\theta) - A(\eta(\theta)) \right)
$$
我们模型使用到的分布都是属于指数分布族,因此利用指数分布族的一些性质,能够大大简化优化过程。充分统计量$T(\beta)$的期望等于Log Normalizer $A_g(\lambda)$的导数。
下文$\beta$是变量,$\lambda$是该变量所属分布的参数,且该分布属于指数分布族,因此$\lambda$就是自然参数。一定要区分清哪些是变量,哪些是参数。

指数分布族形式的分布,优化ELBO会得出如下结论。

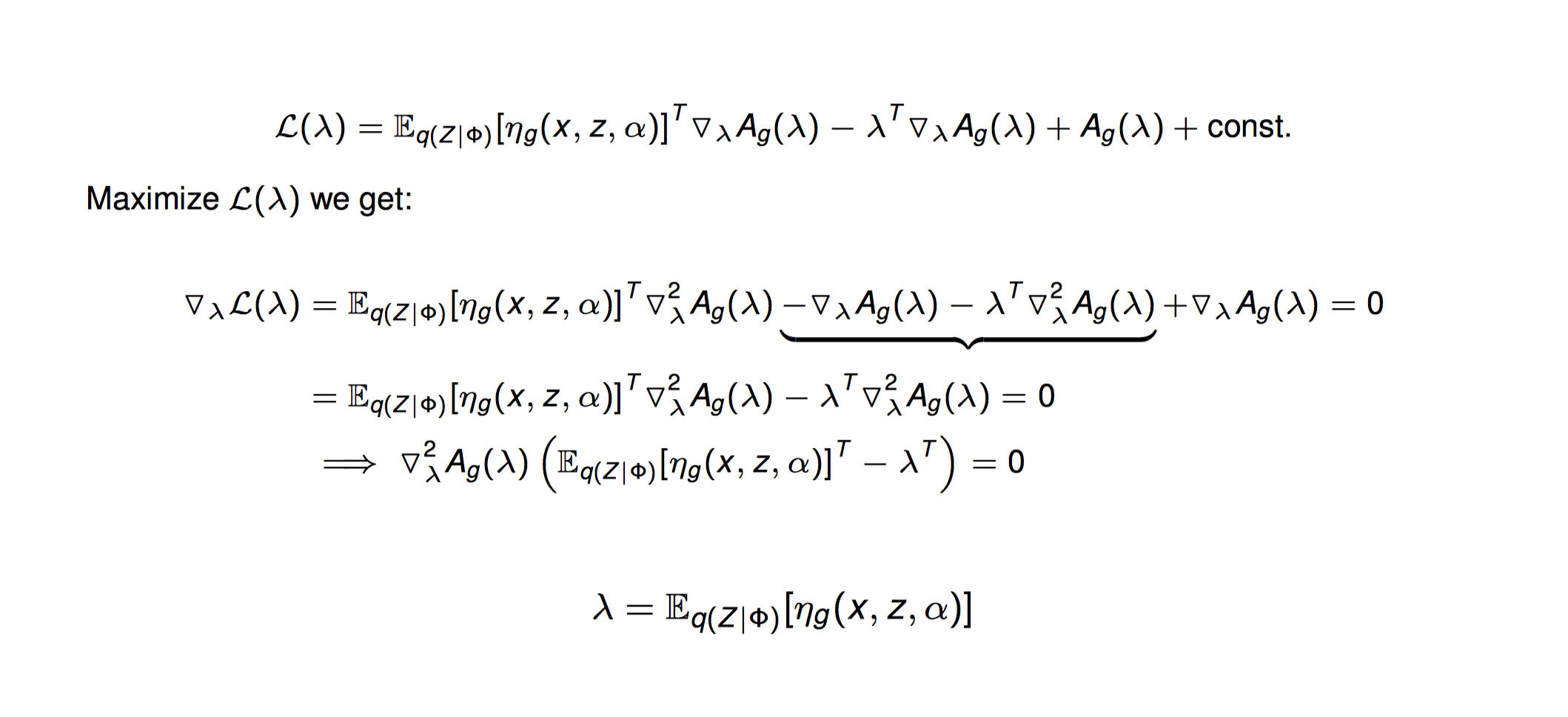
即,如果某个隐变量的分布($q(z_j)$)属于指数分布族,并且该隐变量分布($q(z_j)$)和对应的模型的后验概率分布($p(z_j|z_{-j},x)$)的指数分布族形式一样,则优化ELBO时,该隐变量的自然参数的迭代公式等于其他变量的自然参数的期望。该性质能够保证要优化的参数不会出现在迭代公式中。这样就能使用坐标提升法来优化。
因此问题的关键在于如何得到其他隐变量的自然参数形式。可以看出,上述$\eta_g(x,z,\alpha)$是在求要优化的隐变量$\beta$的后验概率,然后转成指数分布族形式得到的。因此问题的关键在于如何表示隐变量的后验概率,以及如何转成指数分布族的形式,并求出自然参数。
平均场理论
$$
q(Z)=\prod_{i=1}^M q_i(z_i)
$$
这个理论在上述最后结论求期望的时候需要用到。即不同参数的联合期望可以分解成各自参数期望的积。
推导
本部分将使用变分推断来优化上述问题。将使用到ELBO、指数分布族性质、平均场理论。
首先看下我们的概率图模型。

第一步:先找出所有的变量
隐变量:$\xi_u,\theta_u,\eta_i, \beta_i$共4个。
显示变量:$y_{ui}$。
因为我们一般优化的时候是一维一维的进行,因此优化$\theta_u$时,会依次优化$\theta_{uk}$,同理$\beta_{ik}$。这里考虑到,$\theta_u^T \beta_i$会以点乘的形式出现,引入辅助变量$z_{uik}$代表$\theta_{uk}\beta_{ik}$。$y_{ui}=\sum_k z_{uik}$。这个约束非常关键。单独看$z_{uik}$是泊松分布,但是加了这个条件之后,在$y_{ui}$的条件(coditional)下,$z_{uik}|y_{ui}$服从的是多项式分布!!
引入的辅助变量:$z_{uik}$。相当于在原始概率图中,添加一个变量$z_{uik}$,$\theta_{uk}$和$\beta_{ik}$指向$z_{uik}$。另外,$z_{uik}$受${y_{ui}}$的约束,因此$y_{ui}$指向$z_{uik}$。
第二步:写出变量的假设分布

$$
\xi_u \sim Gamma(a^{\prime}, a^{\prime}/b^{\prime}) \\
\theta_{u,k} \sim Gamma(a,\xi_u) \\
\eta_i \sim Gamma(c^{\prime}, c^{\prime}/d^{\prime}) \\
\beta_{ik} \sim Gamma(c, \eta_i) \\
y_{ui} \sim Possion(\theta_{u}^T \beta_i) \\
z_{uik}|\boldsymbol{y_{ui}},\theta_u,\beta_i \sim Mult(\boldsymbol{y_{ui}}, \frac{\theta_{uk}\beta_{ik} }{\sum_{k{\prime}} \theta_{uk^{\prime}}\beta_{ik^{\prime}}}) 。
$$
很关键的一点是,根据泊松分布的可加性,单独的$z_{uik}$是服从泊松分布的。但是加了条件$y_{ui}$之后, 上述$z_{uik}$服从的是多项式分布。
上述是这些隐变量的假设的真实分布。上述等价于:
$$
p(\xi_u|a^{\prime},b^{\prime}) = Gamma(a^{\prime}, a^{\prime}/b^{\prime}) \\
p(\theta_{u,k}|a,\xi_u) = Gamma(a,\xi_u) \\
p(\eta_i|c^{\prime},d^{\prime}) = Gamma(c^{\prime}, c^{\prime}/d^{\prime}) \\
p(\beta_{ik}|c,\eta_i) = Gamma(c, \eta_i) \\
p(z_{ui}|\theta_{u},\beta_{i}, \boldsymbol{y_{ui}}) =Mult(\boldsymbol{y_{ui}}, \frac{\theta_{u}\times\beta_{i} }{\sum_{k{\prime}} \theta_{uk^{\prime}}\beta_{ik^{\prime}}}) \\
p(y_{ui}|\theta_u,\beta_i) = Possion(\theta_{u}^T \beta_i)
$$
一定要区分变量和参数。写成$\sim$形式的,左边代表变量,对于一维概率密度函数而言,就相当于横坐标,也就是样本,一般这种形式用来表示通过概率密度函数抽样得到样本。写成$p$形式的,左边的是概率密度值,相当于纵坐标。不要写出$p(\theta) \sim Gamma(a,b)$这种形式。粗体只是起强调作用。
第三步:写出隐变量的$q$分布
定义不同隐变量的$q$分布。在我们的应用中,$q$分布都假设成指数分布族中的分布,每个分布指定参数(参数向量)。具体的分布形式要根据参数的后验分布来定,通常我们都使用到共轭先验分布,此时后验分布和参数的先验分布一致。
$$
q(\beta_{ik}|\lambda_{ik}) = Gamma(\lambda_{ik}^{shp}, \lambda_{ik}^{rte}) \\
q(\theta_{uk}|\gamma_{u,k}) =Gamma(\gamma_{uk}^{shp}, \gamma_{uk}^{rte}) \\\\
q(\xi_u | \mathcal{k}_u) = Gamma(k_{u}^{shp}, k_{u}^{rte}) \\
q(\eta_i | \tau_i) = Gamma(\tau_{i}^{shp}, \tau_i^{rte}) \\
q(z_{ui}|\phi_{ui}) = Mult(y_{ui}, \phi_{ui})
$$
第四步:根据概率图写出要优化的变量的后验概率
假设要优化$\theta_{uk}$。首先找出和$\theta_{uk}$相关的变量。和$\theta$直接相连的变量是$\xi_u,z_{uik}, y_{ui}$,$\beta_i$和$\theta_u$是co-parent($z_{uik}$)的关系,因此也是相关的。
$$
p(\theta_{uk}|\xi_u, y_{ui},z_{uik}, \beta_{ik}) \propto p(\theta_{uk}|\xi_u) \times \prod_{i=1}^n p(z_{uik}|\theta_{uk},\beta_{ik}, y_{ui})
$$
将后验写成先验$\times$似然的形式。根据概率图,$\theta_{uk}$的先验和$\xi_u$相关。数据似然,就看$\xi_u,z_{uik}, \beta_i, y_{ui}$中哪些是依赖于$\theta_{uk}$的,我们发现$z_{uik}$依赖于$\theta_{uk}$。而$z_{uik}$又依赖于$\beta_{ik},y_{ui}$,因此可以写出上述形式。注意,计算数据似然的时候,要看变量$\theta_{uk}$是被哪些数据共享的。我们不难发现,$\theta_{uk}$是被用户$u$所有的交互数据物品$i$所共享的,或者也可以直接看$z_{uik}$,因此需要对该用户的所有交互物品做乘积。
注意,上述使用的还是假设的真实分布,还没使用到$q$。
这一步是最重要的,变量之间的依赖关系很重要。
第五步:将后验概率形式转成指数家族的分布形式
$$
p(\theta_{uk} | \xi_u,y_{ui}, z_{uik}, \beta_{ik}) \propto p(\theta_{uk}|a,\xi_u) \times \prod_{i=1}^n p(z_{uik}|\theta_{uk},\beta_{ik}, y_{ui}) \\
= exp \left( log(p(\theta_{uk}|a,\xi_u)) + \sum_{i=1}^n log p(z_{uik}|\theta_{uk},\beta_{ik}) \right)
$$
代入这几个分布的函数形式,
$$
p(\theta_{u,k} | a,\xi_u) = Gamma(a,\xi_u)=\frac{ {\xi_u}^a{\theta_{u,k}}^{a-1}e^{-\xi_u \theta_{uk}}}{\Gamma(a)} \\
p(z_{uik}|\theta_{uk},\beta_{ik}) = Possion(\theta_{uk}\beta_{ik})=\frac{e^{-\theta_{uk}\beta_{ik}}(\theta_{uk}\beta_{ik})^{z_{uik}}}{z_{uik}!}
$$
$$
p(\theta_{uk}|\xi_u,y_{ui}, z_{uik}, \beta_{ik}) \propto exp \left(alog\xi_u+(a-1)log \theta_{uk}-\xi_u\theta_{uk} + \sum_{i=1}^n (z_{uik}log(\theta_{uk}\beta_{ik})-\theta_{uk}\beta_{ik}-log{z_{uik}!})\right)
$$
把充分统计量$T(\theta_{uk})$相关的项找出来:
$$
T(\theta_{u,k})=[log \theta_{u,k}, -\theta_{uk} ]^T
$$
$$
p(\theta_{uk}|\xi_u,y_{ui}, z_{uik}, \beta_{ik}) \propto exp \left( T(\theta_{u,k})^T [a-1+\sum_{i=1}^n z_{uik}, \xi_u+n\beta_{ik}] + A(\eta(\xi_u,z_{uik}, \beta_{ik})) \right)
$$
因此找到了自然参数,$\eta(\xi_u,z_{uik}, \beta_{ik})=[a-1+\sum_{i=1^n} z_{uik}, \xi_u+\sum_{i=1}^n \beta_{ik}]$,这是二维的,因为$\gamma$分布有2个参数。
第六步:更新自然参数
又:$q(\theta_{uk}|\gamma_{u,k}) =Gamma(\gamma_{uk}^{shp}, \gamma_{uk}^{rte}) \\\\$, 要更新的参数为$\gamma_{u,k}$
$$
\eta(\gamma_{uk})=E_{q(\xi_u,z_{uik},\beta_{ik})}([a-1+\sum_{i=1}^n z_{uik}, \xi_u+\sum_{i=1}^n \beta_{ik}] )
$$
$$
\eta(\gamma_{uk}^{shp})=E_{q(\xi_u,z_{uik},\beta_{ik})}(a-1+\sum_{i=1}^n z_{uik}) \\
\eta(\gamma_{uk}^{rte})=E_{q(\xi_u,z_{uik},\beta_{ik})}( \xi_u+\sum_{i=1}^n \beta_{ik}) \\
$$
根据平均场理论,$q(\xi_u,z_{uik},\beta_{ik})=q(\xi_u|k_u)q(z_{uik}|\phi_{uik})q(\beta_{ik}|\lambda_{ik})$。自然参数中只有$z_{uik}$,因此只和$q(z_{uik}|\phi_{uik})$有关。
$$
\eta(\gamma_{uk}^{shp})=E_{q(\xi_u,z_{uik},\beta_{ik})}(a-1+\sum_{i=1}^n z_{uik})=a-1 + E_{q(z_{uik}|\phi_{ui})}(\sum_{i=1}^n z_{uik}) \\
= a-1 + \sum_{i=1}^n E_{q(z_{uik}|\phi_{uik})}[z_{uik}]=a-1+\sum_{i=1}^n y_{ui}\phi_{iuk}
$$
上述是根据多项式分布的期望,$E_q[z_{uik}]=y_{ui}\phi_{iuk}$.
同理:
$$
\eta(\gamma_{uk}^{rte})=E_{q(\xi_u|k_u)}( \xi_u) + E_{q(\beta_{i,k}|\lambda_{i,k})}(\sum_{i=1}^n \beta_{ik}) \\
= \frac{k_u^{shp}}{k_u^{rte}} + \sum_{i=1}^n \frac{\lambda_{i,k}^{shp}}{\lambda_{i,k}^{rte}}
$$
上述期望利用的是Gamma分布的期望的性质,$E_{q(a,b)}[X]=\frac{a}{b}$
第七步:转成传统参数
上述更新的是自然参数,我们要更新的是原本分布中的参数。原本的分布:$q(\theta_{uk}|\gamma_{u,k}) =Gamma(\gamma_{uk}^{shp}, \gamma_{uk}^{rte})$
将$X \sim Gamma(a,b)$分布转成指数分布族形式,忽略常数:
$$
exp\left(log \frac{b^a x^{a-1}e^{-bx}}{\Gamma(a)} \right) \propto exp((a-1) log x -bx + A(\eta(a,b)))
$$
因此,$\eta(a,b) = [a-1, b]$。 即,$\eta(a)=a-1, \eta(b)=b$,因此:
$$
\gamma_{uk}^{shp} = \eta(\gamma_{uk}^{shp} )+1=a -1+\sum_{i=1}^n y_{ui}\phi_{iuk}+1=a+\sum_{i=1}^n y_{ui}\phi_{iuk}
$$
$$
\gamma_{uk}^{rte}=\eta(\gamma_{uk}^{rte})= \frac{k_u^{shp}}{k_u^{rte}} + \sum_{i=1}^n \frac{\lambda_{i,k}^{shp}}{\lambda_{i,k}^{rte}}
$$
因此,上述就是$\gamma$的迭代公式。
其他参数的推导同理。如$z_{ui}$变量的参数$\phi_{ui}$更新推导如下。
- 写出后验:例如:对于$z_{ui}$, 后验等于先验,因为其余隐变量$\theta_u,\beta_i, y_{ui}$没有依赖于$z_{ui}$的。$z_{ui}$是向量形式,$K$维。
$$
p(z_{ui}|\theta_u,\beta_i, y_{ui}) = Mult(\boldsymbol{y_{ui}}, \frac{\theta_{u}*\beta_{i} }{\sum_{k{\prime}} \theta_{uk^{\prime}}\beta_{ik^{\prime}}}) \\
\propto \prod_{k}^K (\theta_{uk}\beta_{ik})^{z_{uik}}
$$
转成指数分布族形式,
$$
p(z_{ui}|\theta_u,\beta_i, y_{ui}) \propto exp (\sum_{k=1}^K z_{uik} log (\theta_{uk} \beta_{ik}) ) \\
= exp([z_{ui1}, z_{ui2}, …, z_{uik}, …, z_{uiK}]^T [log {\theta_{u1}\beta_{i1}}, log {\theta_{u2}\beta_{i2}}, …, log {\theta_{uK}\beta_{iK}}])
$$
自然参数为 $[log {\theta_{u1}\beta_{i1}}, log {\theta_{u2}\beta_{i2}}, …, log {\theta_{uK}\beta_{iK}}]$。更新参数
$$
\eta(\phi_{ui}) = log(\phi_{ui}) \propto E_{q(\theta_u,\beta_i)}[log {\theta_{u1}\beta_{i1}}, log {\theta_{u2}\beta_{i2}}, …, log {\theta_{uK}\beta_{iK}}] \\
= E_{q(\theta_u)}[log \theta_{u1}, …, log\theta_{uK}] + E_{q(\beta_i)}[log\beta_{i1}, ,…, log \beta_{iK}]
$$
单独看1项:
$$
\eta(\phi_{uik}) =E_{q(\theta_u)}[log \theta_{uk}] + E_{q(\beta_i)}[log\beta_{ik}] \\
= \varphi(\gamma_{uk}^{shp})- ln(\gamma_{uk}^{rte}) + \varphi(\lambda_{ik}^{shp})-ln(\lambda_{ik}^{rte})
$$更新传统参数
$$
\phi_{uik} = exp \left(\varphi(\gamma_{uk}^{shp})- ln(\gamma_{uk}^{rte}) + \varphi(\lambda_{ik}^{shp})-ln(\lambda_{ik}^{rte}) \right)
$$

