本文对word2vec中常见的CBOW(continuous bag-of-word)、 SG(Skip-Gram)模型进行总结,包括优化技术Hierachical Softmax和Negative Sampling。 word2vec模型学习到的词向量表示携带着丰富的语义信息,能够应用到NLP、推荐系统等多种应用的建模中。本文会系统的总结一下word2vec的方法,主要参考《word2vec Parameter Learning Explained》。
基本定义
所有单词构成的词典大小为$V$。
要学习的单词的词向量维度为$N$。
一个单词最原始的表示,使用one-hot方式。$(x_1,x_2,…,x_k,…,x_V)$,其中, $x_k = 0/1, \ \forall k=1,2,…,V$。
假设某个单词$w$在字典中对应的下标为$k$, 则$x_k=1$, $x_{k^{\prime}} \neq 1, \text{for}\ k^{\prime} \neq k$。
一个训练样本实例(training instance)为$(w_I, w_O)$, 即单词pair对。$w_I$称为输入单词,可理解成机器学习中的特征,$w_O$称为输出单词,可理解成机器学习中的标签,我们的目标是利用$w_I$来预测$w_O$。 在CBOW模型中,$w_I$为若干个上下文词,$w_O$为中心词(或称为目标词),因此CBOW要利用上下文词来预测中心词。在Skip-Gram模型中,$w_I$为中心词,$w_O$为若干个上下文词,因此Skip-Gram要利用中心词来预测上下文词。
输入向量$\text{Input Vector}$: 输入单词$w_I$的输入向量表示为$v_{w_I}$。
输出向量$\text{Output Vector}$:输出单词$w_O$的输出向量表示为$v^{\prime}_{w_O}$。对于给定的输入单词$w_I$, 可能的输出单词有$V$种,不防令可能的输出单词下标为$j(0 \leq j < V)$, 则输出单词$w_j$的输出向量表示为$v^{\prime}_{w_{j}}$。我们通常用$j$表示可能的输出单词的下标,因此通常要计算$p(w_j|w_I)$。
对于一个单词$w$,有一个输入向量$v_w$,还有一个输出向量$v^{\prime}_w$。因为这个单词既可以作为中心词出现,也可以作为上下文词出现。通常最后我们只采用学习到的输入词向量,输出词向量不用。
CBOW
CBOW最早是Mikolov等大牛在2013年提出的。CBOW要利用若干个上下文词来预测中心词。之所以称为continuous bag-of-word,即连续词袋,是因为在考虑上下文单词时,这些上下文单词的顺序是忽略的。我们先从最简单版本的CBOW开始讲,即上下文词只有1个。
One-word context
先从最简单的CBOW开始讲,即只使用1个上下文单词$w_I$来预测中心词$w_O$。
如图1描述的就是One-word context定义之下的神经网络模型。词典大小为$V$, 隐藏层的大小为$N$,相邻层的神经元是全连接的。输入层是一个用one-hot方式编码的单词向量$x=(x_1,…x_k,…,x_V)$,其中只有一个$x_k$为1,其余均为0。
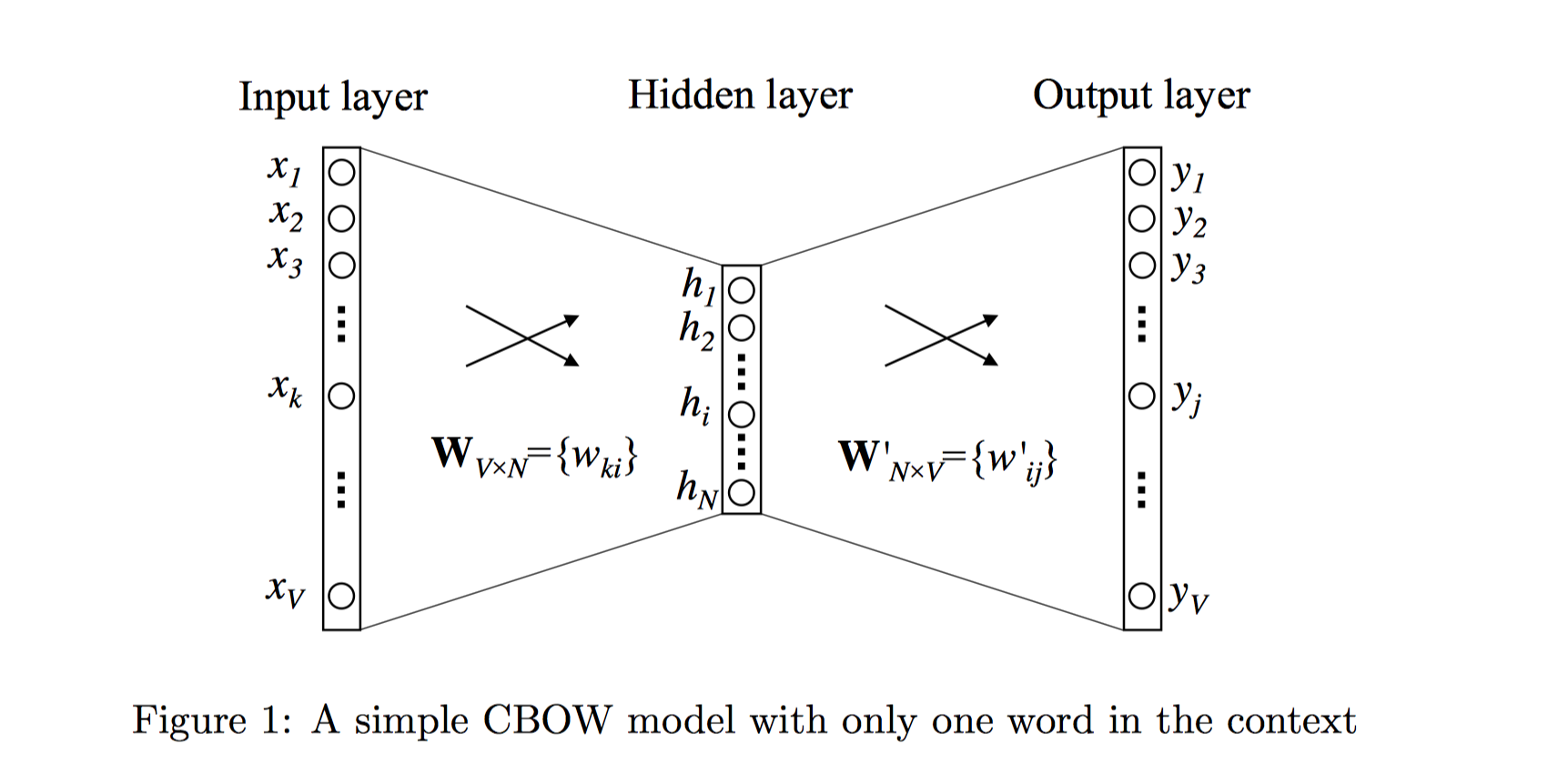
输入层到隐藏层
从输入层到隐藏层的连接权重可以使用矩阵$\mathbf {W}_{V \times N}$来表示:
$$
\mathbf W=
\begin{pmatrix}
w_{11}& w_{12}& …& w_{1N}\\
w_{21}& w_{22}& … & w_{2N}\\
…& … & … & …\\
w_{V1}& w_{V2}&. .. &w_{VN}
\end{pmatrix}
$$
$\mathbf W_{V\times N}$每行是相应单词的输入词向量表示,即第一行为词典中第一个单词的输入词向量表示,第$k$行为词典中第$k$个词的输入词向量表示,解释如下:
$$
\mathbf h= \mathbf W^T \mathbf x=\mathbf W_{(k,\cdot)}^T :=\mathbf v_{\omega_I}^T \tag{1}
$$
$x$是某个单词的one-hot向量表示,且该单词在词典中的下标为$k$,即$x_k=1$, $x_{k^{\prime}}=0, \ k^{\prime} \neq k$。因此只用到$W^T$的第$k$列,也即$\mathbf W$的第$k$行。因此,$\mathbf W$的第$k$行即为第$k$个单词的输入词向量,相当于直接将$\mathbf W$的第$k$行拷贝到隐藏层单元$\mathbf h$上。该输入词向量也是我们最终学习到的词向量(后面的输出词向量我们不需要)。
在上述神经网络中,相当于输入层到隐藏层的激活函数为线性激活函数。另外,由于具有上述的性质,因此通常输入层到隐藏层不显示绘制出来,直接通过查表操作(如TensorFlow中embedding_lookup)拿出单词的词向量,然后传入到下一层,只不过这个词向量也需要通过反向传播来优化。
隐藏层到输出层
从隐藏层到输出层,同样有连接权重矩阵$\mathbf W^{\prime}_{N \times V}={w^{\prime}_{ij}}$来表示。注意,$\mathbf W$和$\mathbf W^{\prime}$不是转置的关系,是不同的两个矩阵。$\mathbf W^{\prime}$用于预测输出词向量。
$$
\mathbf W’=
\begin{pmatrix}
w_{11}^{\prime}& w_{12}^{\prime}&… & w_{1V}^{\prime}\\
w_{21}^{\prime} &w_{22}^{\prime}&…&w_{2V}^{\prime}\\
…&…&…&…\\
w_{N1}^{\prime} &w_{N2}^{\prime}&…&w_{NV}^{\prime}
\end{pmatrix}
$$
$\mathbf W^{\prime}$的每一列可以解释为相应单词的输出词向量,即:第一列为词典中第一个单词的输出词向量表示,第$k$列为词典中第$k$个词的输出词向量表示,记做$v^{\prime}_{w_k}$。
计算输出层每个单元$j$的未激活值,这个$j$就是基本定义中的输出单词(标签)在词典中的下标。
$$
u_j = {v^{\prime}_{w_j}}^T h \tag{2}
$$
$v^{\prime}_{w_j}$是$\mathbf W^{\prime}$的第$j$列,$h$实际上就是某个样本对$(w_I,w_O)$中的$w_I$的输入词向量(CBOW中为上下文词的输入词向量),当$O=j$时,$v^{\prime}_{w_j}$实际上就是$w_O$的输出词向量(CBOW中为中心词的输出词向量),因此$u_j$衡量了二者的相似性,也就是共现性。
计算输出层每个单元$j$的激活值,使用$\text{softmax}$激活函数,这个激活值就是用来近似输出单词的后验概率分布,该分布是词典上所有单词的多项式分布:$Mult(V, \mathbf p(w_j|w_I)), j=1,2…,V$,即词典上所有输出单词$w_j$都有一个作为上下文单词$w_I$的中心词的概率,所有概率和为1。
$$
p(w_j|w_I) = y_j = softmax(u_j) = \frac{exp(u_j)}{\sum_{j^{\prime}=1}^V exp(u_{j^{\prime}})} \tag{3}
$$
$y_j$是第$j$个输出神经元的激活值。
(1)、(2)代入(3)得到:
$$
p(w_j|w_I)=\frac{\exp({\mathbf v_{w_j}’}^T \mathbf v_{w_I})}{\sum_{j’=1}^V\exp({\mathbf v_{w_j}’}^T \mathbf v_{w_I})} \tag{4}
$$
我们的优化目标是,对于$j=O, p(w_j|w_I) \rightarrow 1$, 对于$j \neq O, p(w_j|w_I) \rightarrow 0$。
但是这个式子是优化难点,分母上需要计算每个输出单词的未激活值,计算复杂度太高。这也是后面优化技术出现的原因。
再强调一遍,对于某个单词$w$,$v_w$和$v^{\prime}_w$是单词的两种向量表示形式。其中$v_w$实际上是权重矩阵$\mathbf W$(input->hidden)的某一行向量,$v^{\prime}_w$则是权重矩阵$\mathbf W^{\prime}$(hidden->output)的某一列向量。前者称作输入向量,后者称作输出向量。
优化
下面将推导上述神经网络版本的优化方法。实践中该方法肯定是行不通的,因为复杂度太高。此处优化推导主要为了加深理解。
该模型训练的目标是最大化公式(4)的对数似然。公式(4)代表的就是给定上下文单词$w_I$以及其权重矩阵的情况下,预测其实际输出中心词$w_O$的条件概率。
这里使用的损失函数实际上是交叉熵损失函数$E = - \sum_j t_j log p(x_j)$($x_j$理解为输入one_hot样本,p理解为整个神经网络, 因此$p(x_j)$在该问题中就是最终的输出神经元激活值$y_j$)。
$t_j$是样本$x_j$的真实标签,对于某个样本实例,在输出神经元上,只有一个分量的$t_j=1$,其余为0,不妨令这个分量为$j^{*}$。化简即:$E=-log p(w_O|w_I)$为本问题的交叉熵损失函数。推导:对于单样本而言,最大化似然概率:
$$
\begin{align}
& \max p(w_O|w_I)=\max y_{j^{*}} \tag{5}\\
&=\max \log y_{j^{*}} \tag{6}\\
&=u_{j^{*}} - \log \sum_{j^{\prime}=1}^V \exp(u_{j^{\prime}}):=-E \tag{7}
\end{align}
$$
即:
$$
E = -u_{j^{*}} + log \sum_{j^{\prime}=1}^V exp(u_j^{\prime})
$$
接下来使用梯度下降和误差反向传播进行优化,这部分比较简单,具体推导不细说,下面是对单个样本实例的更新公式。
输出层到隐藏层
- 先求$E$对$u_j$的导数:
$$
\frac{\partial E}{\partial u_j}=y_j-t_j:=e_j \tag{8}
$$
当$j = j^{*}$时,$t_j = 1$, 否则$t_j=0$。(损失的第一项)、损失第二项求导后就是激活值$y_j$。
再求$E$关于权重矩阵$\mathbf W^{\prime}$的元素$w_{ij}^{\prime}$的导数,一个元素$w_{ij}^{\prime}$只和隐藏层神经元$h_i$、输出层未激活神经元$u_j$相连接。
$$
\frac{\partial E}{\partial w_{ij}’}=\frac{\partial E}{\partial u_j}\cdot \frac{\partial u_j}{\partial w_{ij}^{\prime}}=e_j\cdot h_i \tag{9}
$$使用SGD更新$w_{ij}^{\prime}$:
$$
\begin{align}
{w_{ij}^{\prime}}^{(new)}={w_{ij}^{\prime}}^{(old)}-\eta \cdot e_j \cdot h_i\tag{10}
\end{align}
$$
或者一次性更新输出神经元$j$对应的单词$w_j$的输出词向量$\mathbf v_{w_j}$,也即$\mathbf W^{\prime}$的第$j$列(输出神经元$j$的误差$e_j$传播到和它相连的权重向量$\mathbf v_{w_j}$)
$$
\begin{align}
{\mathbf v_{w_j}^{\prime}}^{(new)}= {\mathbf v_{w_j}^{\prime}}^{(old)} - \eta \cdot e_j \cdot \mathbf h \space \space \text{for} \ \ j=1,2,…V.\tag{11}
\end{align}
$$
由公式(11)可以看出,在更新权重参数的过程中,我们需要检查词汇表中的每一个单词,计算出它的激活输出概率$y_j$(源于多分类,softmax分母),并与期望输出$t_j$(取值为0或者1)进行比较,$t_j$实际上就是真实标签,对于某个样本,若某个输出词为该样本的中心词,则为1,否则为0。也就是说,对于某个样本实例$(w_I,w_O)$,不仅要计算$p(w_O|w_I)$, 还要计算$p(w_j|w_I),\ j=1,2…,V$。对于某个样本实例$(w_I,w_O)$,我们希望优化的结果是,对于真实中心词$w_O$,$p(w_O|w_I)$概率接近1,对于其他非真实中心词$w_j$, $p(w_j|w_I)$概率接近0。梯度更新解释性如下,
1)如果$y_j>t_j$(“overestimating”),则预测$w_j$作为中心词的概率值过大了,也就是说这个输出词$w_j$没有这么大可能作为上下文词$w_I$的中心词,或者说这个中心词和上下文词差别应当更大。那么优化的结果,就从向量$v_{w_j}^{\prime}$中减去隐藏向量$h$的一部分(即上下文词$w_I$的输入词向量$v_{w_I}$),这样向量$v_{w_j}^{\prime}$就会与向量$v_{w_I}$相差更远。
2)如果$y_j<t_j$(“underestimating”),这种情况只有在$t_j=1$时才会发生,此时$w_j=w_O$,也就是预测$w_j$作为中心词的概率值过小了,这个输出词$w_j$有很大可能就是上下文词$w_I$的中心词,或者说这个中心词和上下文词差别很小。那么优化的结果是,将隐藏向量$h$的一部分加入$v^{\prime}_{w_O}$,使得$v^{\prime}_{w_O}$与$v_{w_I}$更接近。
3)如果$y_j$与$t_j$非常接近,则此时$e_j$非常接近于0,故更新参数基本上没什么变化。上述远近是针对向量内积而言,也即在向量空间中两个点的距离。可以证明:
$$
(v+\alpha h)^T \cdot h > v^T \cdot h \rightarrow \text{加上h的某比例分量,则和h更接近} \\
(v-\alpha h)^T \cdot h < v^T \cdot h \rightarrow \text{减去h的某比例分量,则和h更远离} \\
\alpha > 0
$$
隐藏层到输入层
先求$E$对隐藏层神经元$h_i$的偏导,$h_i$和所有输出神经元$j$都有连接,故求和计算收集到的所有误差。
$$
\frac{\partial E}{\partial h_i} = \sum_{j}^V \frac{\partial E}{\partial u_j} \cdot \frac{\partial u_j}{\partial h_i} = \sum_j e_j w_{ij}^{\prime} :=EH_i \tag{12}
$$
$\mathbf{EH}$是$N$维向量,$\mathbf{EH}=\mathbf W^{\prime}_{N\times V} \cdot \mathbf{e}_{V \times 1}=\sum_{j=1}^{V} e_j \times \mathbf{v}_{j}^{\prime}$再求$E$对$\mathbf W$元素$w_{ki}$的导数, $h_i$和$w_{ki}, k=1,2…,V$权重相连。
$$
h_i=\sum_{k=1}^V x_k \cdot w_{ki} \tag{13}
$$
有:
$$
\frac{\partial E}{\partial w_{ki}}=\frac{\partial E}{\partial h_i} \cdot \frac{\partial h_i}{\partial w_{ki}}=EH_i \cdot x_k \tag{14}
$$
对于某个样本而言,只有一个分量$x_k=1$,其余为0,因此一个样本实际上只更新$\mathbf W$的第$k$行向量。写成矩阵更新的形式:
$$
\begin{align}
\frac{\partial E}{\partial \mathbf W}
&=
\begin{pmatrix}
\frac{\partial E}{\partial w_{11}}& \frac{\partial E}{\partial w_{12}}& …& \frac{\partial E}{\partial w_{1N}}\\
\frac{\partial E}{\partial w_{21}}& \frac{\partial E}{\partial w_{22}}& … & \frac{\partial E}{\partial w_{2N}}\\
…& … & … & …\\
\frac{\partial E}{\partial w_{V1}} & \frac{\partial E}{\partial w_{V2}} &. .. & \frac{\partial E}{\partial w_{VN}}
\end{pmatrix} \\
&=
\begin{pmatrix}
EH_1 \cdot x_1 & EH_2 \cdot x_1 & …& EH_N \cdot x_1\\
EH_1 \cdot x_2 & EH_2 \cdot x_2 & …& EH_N \cdot x_2\\
…& … & … & …\\
EH_1 \cdot x_V & EH_2 \cdot x_V & …& EH_N \cdot x_V\\
\end{pmatrix} \\
&= \mathbf x \otimes \mathbf{EH} = \mathbf x \mathbf{EH}^T
\end{align} \tag{15}
$$更新输入词向量$v_{w_I}$:
$$
{\mathbf v_{W_I}}^{(new)}={\mathbf v_{W_I}}^{(old)}-\eta \cdot \mathbf {EH}^T \tag{16}
$$
也就是说,对于某个样本而言,上述$x_1,x_2,…,x_V$只有1个值非0。那么式15更新中,只有该行非零,其余行全为0。因此,我们只更新输入上下文词$w_I$对应行的词向量。该梯度更新过程可以使用同样的解释方法,$\mathbf{EH}=\mathbf W^{\prime}_{N\times V} \cdot \mathbf{e}_{V \times 1}$,意味着:
1)如果过高地估计了某个单词$w_j$作为最终输出中心词的概率(即:$y_j>t_j$),相应$\mathbf e$分量$e_j$大于0,则(16)式更新相当于将$\mathbf v_{W_I}$输入上下文词向量第$j$个分量减去输出中心词$v_{w_j}^{\prime}$词向量的第$j$个分量,使得二者远离。
2)如果过低地估计了某个单词$w_j$作为最终输出中心词的概率(即:$y_j<t_j$),相应$\mathbf e$分量$e_j$小于0,则(16)式更新相当于将$\mathbf v_{W_I}$输入上下文词向量第$j$个分量加上输出中心词$v_{w_j}^{\prime}$词向量的第$j$个分量,使得二者接近。
因此,上下文单词$w_I$(context word )的输入向量的更新取决于词汇表中所有单词预测为中心词的误差$\mathbf e$。预测误差越大,则该单词对于上下文单词的输入向量的更新过程影响越大。
Multi-word context
基于multi-word context的CBOW模型利用多个上下文单词来预测中心单词,且不同上下文单词不考虑顺序。神经网络结构如图2所示:
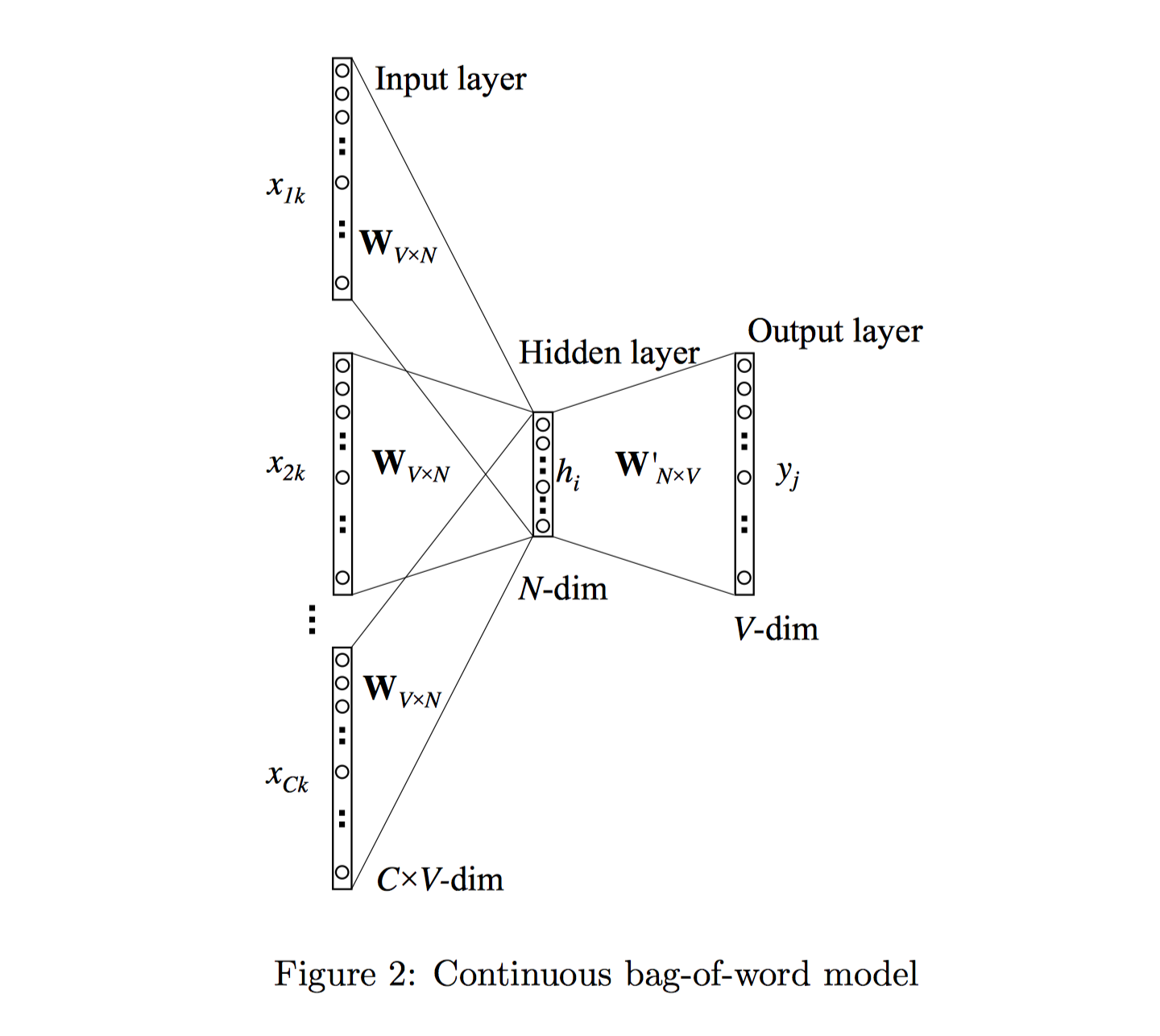
其隐藏层的输出值的计算过程为:首先将输入的上下文单词(context words)的向量相加起来并取其平均值,接着与input→hidden的权重矩阵相乘,作为最终的结果,公式如下:
$$
\begin{align}
& \mathbf h = \frac{1}{C} \mathbf W^T(\mathbf x_1 + \mathbf x_2 + \cdots +\mathbf x_C)\tag{17}\\
& = \frac{1}{C}(\mathbf v_{w_1}+\mathbf v_{w_2} + \cdots+\mathbf v_{w_C})^T\tag{18}
\end{align}
$$
$C$为上下文单词的数量,$w_1,w_2,…,w_C$为上下文单词,$v_{w}$是上下文单词$w$的输入词向量。
损失函数如下:
$$
\begin{align}
& E = - \log p(w_O|w_{I,1},…,\omega_{I,C}) \tag{19}\\
& =- u_{j^{*}} + \log \sum_{j^{\prime}=1}^{V} exp(u_{j^{\prime}})\tag{20}\\
& = - {\mathbf v_{w_O}^{\prime}}^T \cdot \mathbf h + \log \sum_{j^{\prime}=1}^{V} \exp({\mathbf v_{w_j}^{\prime}}^T \cdot \mathbf h)\tag{21}
\end{align}
$$
隐藏层到输出层之间的权重更新完全和上述One-word context一样。
输入层到隐藏层之间的权重更新也与(16)式大致一样,只不过现在要更新$C$个上下文单词的输入词向量。每个更新公式如下:
$$
{\mathbf v_{W_{I,c}}}^{(new)}={\mathbf v_{W_{I,c}}}^{(old)}-\frac{1}{C} \cdot \eta \cdot \mathbf {EH}^T \tag{22}
$$
注意有个$\frac{1}{C}$系数,这是式18导致的。
Skip-Gram
与CBOW模型正好相反,Skip-Gram模型是根据中心词(target word)来预测上下文单词(context words)。模型结构如下图3所示:
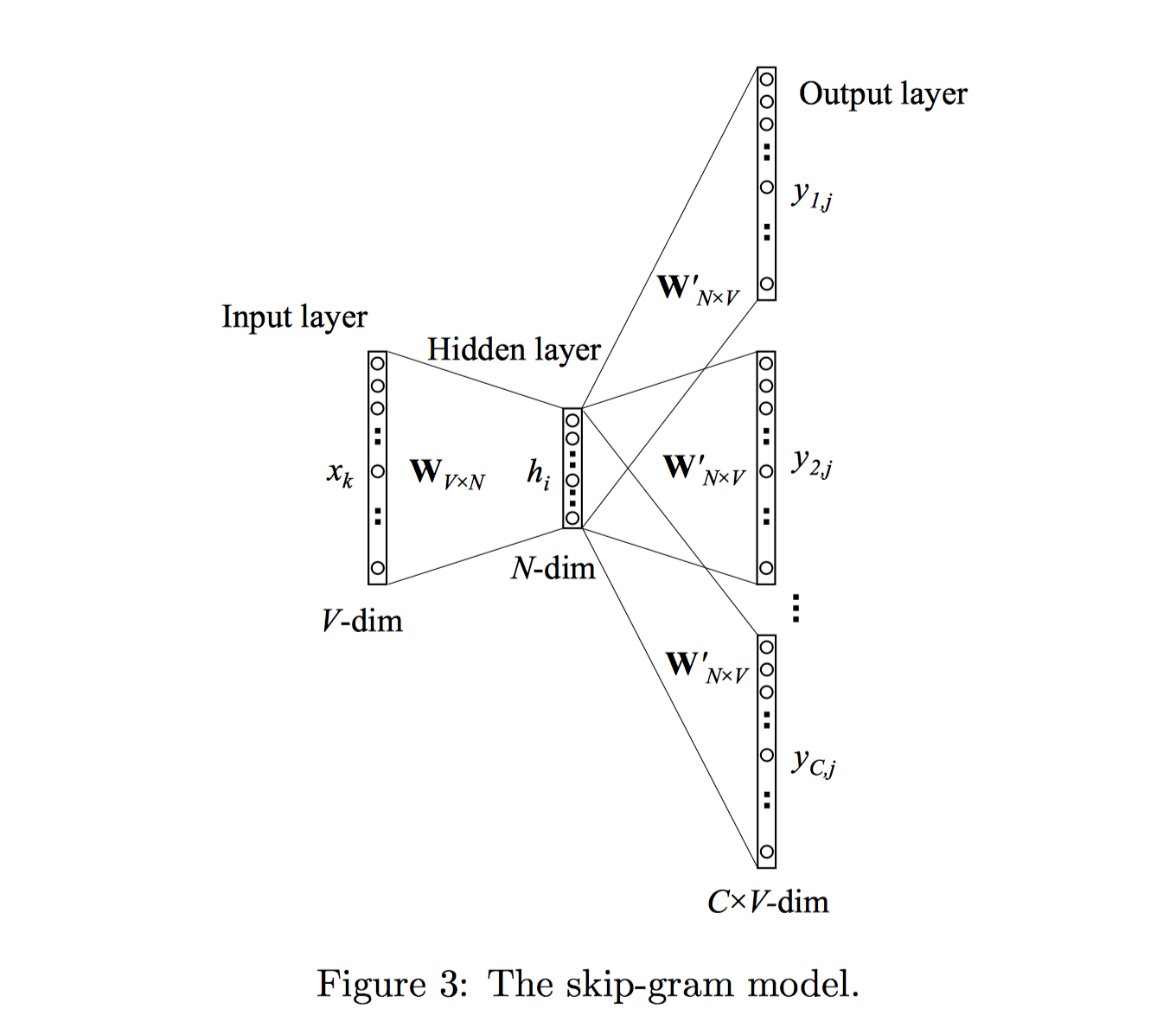
输入层到隐藏层和CBOW一样。隐藏层到输出层输出$C$个多项式分布,每个多项式分布代表第$c$个上下文词位置(c-th panel)上所有单词的概率分布。且$\mathbf W^{\prime}$由C个上下文panel共享。
$$
p(w_{c,j}=w_{O,c}|w_I)=y_{c,j}=\frac{\exp(u_{c,j})}{\sum_{j^{\prime}=1}^V \exp(u_{j}^{\prime})} \tag{23}
$$
$$
u_{c,j}= u_j =\mathbf {v_{w_j^{\prime}}}^T \mathbf h , \ \text{for} \ c=1,2,…,C \tag{24}
$$
其中,$u_{c,j}$代表输出层第$c$个panel的第$j$个神经元的输入值(未激活值)。
其中,$\mathbf {v_{w_j^{\prime}}}$为词汇表第$j$个单词$w_j$的输出向量;也是取自于hidden→output权重矩阵$\mathbf W^{\prime}$的一列。
优化
损失函数如下,各个panel之间独立,因此将各个panel的概率连乘。且每个上下文概率计算过程中,只有一个$t_{c,j}=1$,不妨记做$j_{c}^{*}$,其余$t_{c,j}=0$.
$$
\begin{align}
&E=-\log p(w_{O,1},w_{O,2},…,w_{O,C}|w_I) \tag{25}\\
&=-\log \prod_{c=1}^C \frac{\exp(u_{c,j_c^{*}})}{\sum_{j^{\prime}=1}^V \exp(u_{j^{\prime}})}\tag{26}\\
&=-\sum_{c=1}^C u_{j_c^{*} }+ C \cdot \log\sum_{j^{\prime}=1}^V exp(u_{j^{\prime}})\tag{27}
\end{align}
$$
输出层到隐藏层
计算E对$u_{c,j}$的偏导,即只求每个panel中每个词未激活值的导数:
$$
\frac{\partial E}{\partial u_{c,j}}=y_{c,j}-t_{c,j} :=e_{c,j} \tag{28}
$$
定义$V$维向量,$\mathbf {EI}=\{EI_1, EI_2,…,EI_V\}$, 为不同上下文单词的总预测误差向量。每个分量$EI_{j}$代表词典中第$j$个单词,作为不同panel位置的上下文单词的预测误差和:
$$
EI_j = \sum_{c=1}^C e_{c,j} \tag{29}
$$再求$E$关于权重矩阵$\mathbf W^{\prime}$的元素$w_{ij}^{\prime}$的导数,不同于CBOW,此时,一个元素$w_{ij}^{\prime}$和一个隐藏层神经元$h_i$、$C$个输出层未激活神经元$u_{c,j}$相连接。
$$
\frac{\partial E}{\partial w_{ij}’}=\sum_{c=1}^C \frac{\partial E}{\partial u_{c,j}}\cdot \frac{\partial u_{c,j}}{\partial w_{ij}^{\prime}}=EI_j\cdot h_i \tag{30} \\
$$
和(9)式基本一模一样,只是将$e_j$替换成$EI_j$。也就是说,某个单词$w_j$在CBOW中误差来源只有1个,因为输出中心词只有1个;而在Skip-Gram中,$w_j$可能成为$C$个上下文词,误差来源有C个,因为权重矩阵共享,因此C个panel中,和$h_i$以及$u_{c,j}$相连的权重$w_{ij}^{\prime}$是一样的。因此,$\frac{\partial u_{c,j}}{\partial w_{ij}^{\prime}}=h_i$是公共项,提出来,剩下的项正好是$EI_j$,即$w_j$作为上下文输出词收集的总误差。SGD更新$w_{ij}^{\prime}$:
$$
\begin{align}
{w_{ij}^{\prime}}^{(new)}={w_{ij}^{\prime}}^{(old)}-\eta \cdot EI_j \cdot h_i \tag{31}
\end{align}
$$
或者,
$$
\begin{align}
{\mathbf v_{w_j}^{\prime}}^{(new)}= {\mathbf v_{w_j}^{\prime}}^{(old)} - \eta \cdot EI_j \cdot \mathbf h \space \space \text{for} \ \ j=1,2,…V. \tag{32}
\end{align}
$$
对于每个训练样本$(w_I, w_{O,1},w_{O,2},…,w_{O,C})$,都需要使用上述公式更新词典中每个词的输出词向量。在更新每个词向量时,需要收集该词在不同上下文panel位置上的误差和,然后进行更新。一共需要$V$次更新。
隐藏层到输入层
同样,对于input→hidden权重矩阵$\mathbf W$的参数更新公式的推导过程,除了考虑要将预测误差$e_j$替换为$EI_j$外,其他也与上文公式[12]到公式[16]类似。这里直接给出更新公式:
$$
{\mathbf v_{w_I}}^{(new)}={\mathbf v_{w_I}}^{(old)}-\eta \cdot \mathbf{EH}^T\tag{33}
$$
其中,$\mathbf{EH}$是一个$N$维向量,组成该向量的每一个元素可以用如下公式表示:
$$
EH_i=\sum_{j=1}^V EI_j\cdot w_{ij}^{\prime} \tag{34}
$$
Optimizing Computational Efficiency
每个词都有个输入向量和输出向量。对每个训练样本,输入向量的优化成本不高,因为只有1个,但是输出向量的优化成本很高,需要遍历词典,优化V个输出向量。为了优化输出向量,对每个词,需要计算$u_j$未激活值,$y_j$(或SG中的$y_{c,j}$)激活值,误差$e_j$(或SG中的$EI_j$),最终来更新输出向量$v^{\prime}_{w_j}$.
显然,对于每一个训练样例都要对所有单词计算上述各值,其成本是昂贵的。特别是对于大型的词汇表,这种计算方式是不切实际的。因此为了解决这个问题,直观的方式是限制必须要更新的训练样例的输出向量的数目。一种有效的实现方式就是:hierarchical softmax(分层softmax),另一种实现通过负采样(negative sampling)的方式解决。
实际上,这种复杂性主要原因是我们采用多分类建模的形式,共$V$个类。即认为要预测的单词是所有单词上多项式分布,那么肯定就要拟合所有单词的概率值。1种优化思路就是将多分类改成多个二分类,同时要能够很好、很快的计算训练样本实例的似然值,这种优化思路对应的方法就是hierarchical softmax。另一种优化思路就是能不能每次训练1个样本实例的时候,不全部优化所有单词的输出向量,而是有代表性的优化某些输出向量,这种优化思路对应的方法就是negative sampling。
这两种方法都是通过只优化【输出向量更新】的计算过程来实现的。在我们的公式推导过程中,我们关心的有三个值:(1)$E$,新目标函数;(2)$\frac{\partial E}{\partial \mathbf v_{w_j}^{\prime}}$,输出向量的更新公式;(3)$\frac{\partial E}{\mathbf h}$,输入向量的更新公式。
Hierarchical Softmax
使用Hierarchical Softmax的整体神经网络结构大致是,输入层到隐藏层和上述结构类似,隐藏层神经元和二叉树所有内部节点都有连接,来传递隐向量$h$。整棵二叉树充当了输出层的角色。
Hierarchical softmax 是一种有效的计算 softmax 的方式。该模型使用一棵二叉树来表示词汇表中的所有单词。所有的$V$个单词都在二叉树的叶节点上。可以证明非叶子节点一共有$V−1$个。对于每个叶子节点,从根节点root到该叶子节点只有一条路径;这条路径用来评估用该叶子节点代表的单词的概率值。二叉树的结构如图4所示:
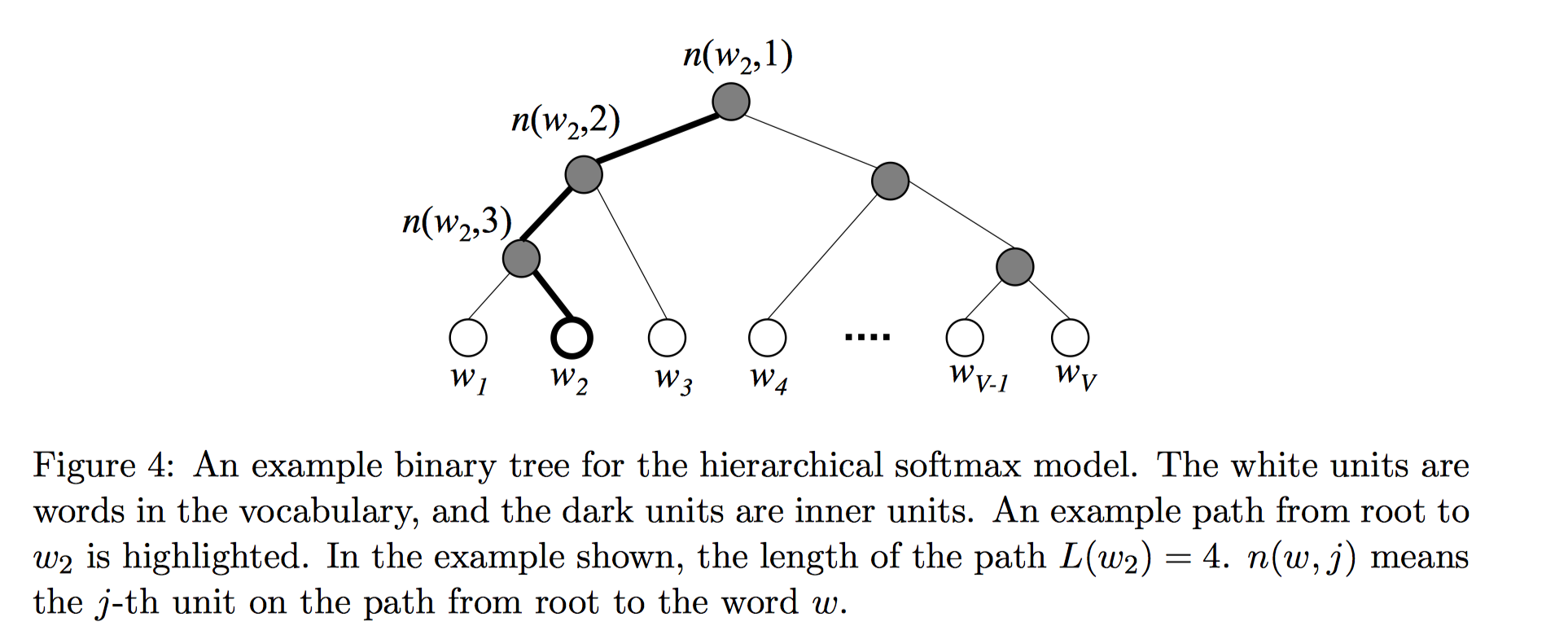
其中白色的树节点代表的是词汇表中的单词,灰色节点为内部节点。图中高亮显示的是一条从根节点到$w_2$的路径。该条路径的长度为$L(w_2)=4$。$n(w,j)$表示从根节点到单词$w$的路径上的第$j$个节点。
在hierarchical softmax模型中,所有的单词没有输出向量表示形式。不同的是,二叉树的每一个内部节点都有一个输出向量$v^{\prime}_{n(w,j)}$。也就是说要学习$V-1$个输出向量。看似没有起到优化的作用,但关键在于,在迭代更新每一个训练样本$(w_I,w_O)$时,不需要优化所有$V-1$个非叶子节点对应的输出向量,只需要优化从根节点到训练样本输出单词$w_O$路径上经过的$O(log V)$量级个非叶子节点的输出向量。且该单词作为输出单词的概率计算公式定义如下:
$$
p(w =w_O)=\prod_{j=1}^{L(w)-1}\sigma \bigg( \left[\! [ n(w,j+1)=ch(n\small(w,j\small)) \right]\!] \cdot{\mathbf v_{n(w,j)}^{\prime}}^T\mathbf h\bigg)\tag{35}
$$
其中,$ch(n)$为节点$n$的左孩子节点;$v^{\prime}_{n(w,j)}$是内部节点$n(w,j)$的向量表示(输出向量);$h$是隐藏层的输出值,在SG模型中,$\mathbf h=v_{w_I}$;而在CBOW模型中,$\mathbf h=\frac{1}{C}\sum_{c=1}^C v_{w_c}$ 。$[\![x]\!]$是一种特殊的函数定义如下:
$$
[\![x]\!]=
\begin{cases}
1 & \text{if $x$ is true} \\
-1, & \text{otherwise}
\end{cases}\tag{36}
$$
上述定义是因为:
$$
p(n,left)=\sigma({\mathbf v_n’}^T\cdot\mathbf h)\tag{37}
$$
$$
p(n,right)=1-\sigma({\mathbf v_n’}^T\cdot\mathbf h)=\sigma(-{\mathbf v_n’}^T\cdot \mathbf h)\tag{38}
$$
以图4为例,假设某个样本的输出值为$w_2$, 式37代表往左走的概率,式38代表往右走的概率。从根节点开始,为了到达$w_2$, 游走序列为左-左-右:
$$
\begin{align}
& p(w_2=w_O)=p\Big(n(w_2,1),left\Big)\cdot p\Big(n(w_2,2),left\Big)\cdot p\Big(n(w_2,3),right\Big)\tag{39}\\
& =\sigma \Big({\mathbf v_{n(w_2,1)}^{\prime}}^T\mathbf h\Big)\cdot\sigma \Big({\mathbf v_{n(w_2,2)}^{\prime}}^T\mathbf h\Big)\cdot\sigma \Big(-{\mathbf v_{n(w_2,3)}^{\prime}}^T\mathbf h\Big)\cdot \tag{40}
\end{align}
$$
可以证明:
$$
\sum_{i=1}^{V}p(w_i=w_O)=1\tag{41}
$$
即所有叶子节点上输出词的概率和为1。
也就是说计算某个输出词的似然概率值时,只需要使用路径上的$L(w)-1$个非叶子节点的输出向量来计算。这里实际上使用的是多个二分类思想,每个非叶子节点就好像是词类型或词主题的向量表示,类似决策树,逐层过滤掉类别后,最终到达某个输出词。
优化
对于某个训练样本$(w_I,w_O)$,我们要优化路径$L(w_O)-1$个内部节点的输出词向量$\mathbf v_j^{\prime}$以及输入单词的词向量$\mathbf v_{w_I}$。
简化公式:
$$
[\![\cdot]\!]:=[\![ n(w,j+1)=ch(n(w,j)) ]\!]\tag{42}
$$
$$
\mathbf v_j^{\prime}:=\mathbf v_{n_{w,j}}^{\prime}\tag{43}
$$
则给定一个训练样本,损失函数为:
$$
E=-\log p(w = w_O|w_I)=-\sum_{j=1}^{L(w)-1}\log\sigma([\![\cdot]\!] {\mathbf v_j^{\prime}}^T\mathbf h)\tag{44}
$$
- 对于误差函数$E$,我们取其关于$\mathbf {v^{\prime}_j}^T \mathbf h$的偏导数,得:
$$
\begin{align}
&\frac{\partial E}{\partial \mathbf v_j’\mathbf h}=\Big(\sigma([\![\cdot]\!]{\mathbf v_j’}^T\mathbf h)-1\Big)[\![\cdot]\!] \tag{45}\\
&=
\begin{cases}
\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-1 ,& [\![\cdot]\!]=1 \\
\sigma({\mathbf v_j^{\prime}}^T\mathbf h), & [\![\cdot]\!]=-1
\end{cases}\tag{46}\\
&=\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j \tag{47}
\end{align}
$$
$t_j=1 \ \text{if} [\![\cdot]\!]=1$, $t_j=0 \ \text{if} [\![\cdot]\!]=-1$。
上式很容易证明,利用sigmoid求导的性质即可。
- 接着,可以计算内部节点$n(w,j)$的输出向量表示$v_j^{\prime}$的偏导数:
$$
\frac{\partial E}{\partial \mathbf v_j^{\prime}}=\frac{\partial E}{\partial \mathbf v_j^{\prime} \mathbf h}\cdot \frac{\partial \mathbf v_j^{\prime} \mathbf h}{\partial \mathbf v_j^{\prime}}=\Big(\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j\Big)\cdot \mathbf h\tag{48}
$$
$$
{\mathbf v_j^{\prime}}^{(new)}={\mathbf v_j^{\prime}}^{(old)}-\eta\Big(\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j\Big)\cdot \mathbf h\space,\space \text{for} \space j=1,2,…,L(w)-1\tag{49}
$$
Hierachical Softmax优化点关键在于式(49),对每个训练样本,只需要更新$L(w)-1$个内部节点的输出向量,大大节省了计算时间。
- 为了使用反向传播该预测误差来学习训练input→hidden的权重,我们对误差函数E求关于隐藏层输出值的偏导数,如下:
$$
\begin{align}
&\frac{\partial E}{\partial \mathbf h}=\sum_{j=1}^{L(w)-1}\frac{\partial E}{\partial \mathbf v_j^{\prime} \mathbf h} \cdot \frac{\partial \mathbf v_j^{\prime} \mathbf h}{\partial \mathbf h} \tag{50}\\
&=\sum_{j=1}^{L(w)-1}\Big(\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j\Big)\cdot \mathbf v_j^{\prime} \tag{51}\\
&=\sum_{j=1}^{L(w)-1} e_j \cdot \mathbf v_j^{\prime} \tag{52}\\
&:= \mathbf{EH} \tag{53}
\end{align}
$$
上述$e_j$是标量,$v_j^{\prime}$是向量。
接下来我们根据公式22就可以获得CBOW模型输入向量的更新公式,这里再写一遍。
$$
{\mathbf v_{W_{I,c}}}^{(new)}={\mathbf v_{W_{I,c}}}^{(old)}-\frac{1}{C} \cdot \eta \cdot \mathbf {EH}^T
$$
对于Skip-Gram模型,这里的做法和前面神经网络中的SG优化过程有点不大一样,前面是把每个单词$C$个误 差先累加起来,作为$\mathbf{EI}$的一个分量$EI_j$(类比这里的$e_j$),然后和$v_j^{\prime}$做点乘。而在这里,我们需要计算上下文单词中的每个单词的$\mathbf{EH}$, 即,重复上述过程C次,每次得到一个$\mathbf {EH}$向量,最后将C个$\mathbf {EH}$累加,得到的向量作为该样本最终的$\mathbf {EH}$。相当于前者先合并,后面步骤相同;后者前面步骤相同,再合并。优化的时候,将$\mathbf{EH}$代入公式33,这里再写一遍。
$$
{\mathbf v_{w_I}}^{(new)}={\mathbf v_{w_I}}^{(old)}-\eta \cdot \mathbf{EH}^T
$$
直观理解
Hierarchical Softmax实际上是对单词进行分组或分类。根节点为最大的类别,子节点是父节点大类别下的小类别,一直划分,直到叶子节点,到达某个具体的词。
我们可以将$\sigma({\mathbf v_j^{\prime}}^T\mathbf h)-t_j$理解为内部节点$n(w,j)$的预测误差$e_j$。即预测输出单词属于某个类别的误差。每一个内部节点的“任务”就是预测其随机游走路径是指向左孩子节点还是指向右孩子节点。每次游走到一个内部节点,询问该单词是否属于该内部节点对应的类别,是则往左走,否则往右走。
$t_j=1$意味着节点$n(w,j)$的路径指向左孩子节点,可以解释为该单词属于这个内部节点对应的类别;$t_j=0$则表示指向右孩子节点,代表该单词不属于这个内部节点对应的类别。每个训练样本决定了唯一一条路径,也就是说真实值$t_j$序列是确定的,那么优化内部节点的目标就是最小化预测类别误差。对于一个训练实例,如果内部节点的预测值非常接近于真实值,则它的向量表示$v^{\prime}_j$的更新变化很小;否则$v^{\prime}_j$向量指向一个适当的方向,使得该实例的预测误差逐渐减小。以上更新公式既能应用于CBOW模型,又能应用于SG模型。当在SG模型中使用该更新公式时,我们需要对$C$个output context words的每一个单词都重复此更新过程,也就是说C个输出上下文词,都需要从二叉树根节点游走到相应的叶子节点,各自优化自己路径上的内部节点1次。更新隐藏层到输入层时,同一个上下文单词带来的内部节点预测误差也要累加C次,并反向传播。参考公式$EI_j = \sum_{c=1}^C e_{c,j}$。上述二叉树构造的方法有很多,但使用Huffman树能够使得计算效率最高,保证越频繁出现的词汇,到达根节点的路径越短。
Nagative Sampling
Negative Sampling模型的思想比Hierarchical Softmax模型更简单。即:在每次迭代的过程中,有大量的输出向量需要更新,为了解决这一困难,Negative Sampling提出了只更新其中一部分输出向量的解决方案。
以Skip-Gram为例,最终输出的上下文单词(正样本)在采样的过程中应该保留下来并更新,同时我们需要采集一些单词作为负样本(因此称为“negative sampling”)。在采样的过程中,可以任意选择一种概率分布。将这种概率分布称为“噪声分布”(noise distribution),用$Pn(w)$来表示,可以根据经验选择一种较好的分布。在 word2vec中,作者使用了一个非常简单的采样分布,叫做unigram distribution。形式为:
$$
P_n(w_j) = \frac{f(w_j)^{3/4}}{\sum_{j^{\prime}=1}^Vf(w_j^{\prime})^{3/4}} \tag{54}
$$
上式,$f(w_j)$是单词$w_j$的权重,使用单词出现的频次来表示。$3/4$是分布的参数,此处是论文中使用的参数。也就是说单词出现的频次越大,越可能被选做负样本。
优化
对于某个训练样本$(w_I,w_O)$,我们要优化真实输出单词的输出词向量$\mathbf v_{w_O}^{\prime}$、被选做负样本的输出单词的输出词向量$\mathbf v_{w_j}^{\prime} $以及输入单词的词向量$\mathbf v_{w_I}$。
对于某个训练样本,word2vec的论文实践证明了使用下面简单的训练目标函数能够产生可靠的、高质量的 word embeddings:
$$
E=-\log \sigma({\mathbf v_{w_O}^{\prime}}^T\mathbf h)-\sum_{w_j\in W_{neg}} \log \sigma({-\mathbf v_{w_j}^{\prime}}^T\mathbf h)\tag{55}
$$
其中$w_O$是该训练样本的真实输出单词(the positive sample),$v^{\prime}_{w_O}$是输出向量;$h$是隐藏层的输出值:在SG模型中,$\mathbf h=v_{w_I}$;而在CBOW模型中,$\mathbf h=\frac{1}{C}\sum_{c=1}^C v_{w_c}$ 。$W_{neg}=\{w_j|j=1,…,K\}$是基于分布$P_n(w)$采样的一系列单词。
类比Hierachical Softmax公式44,这里也都是使用sigmoid函数。第一项是真实输出单词的损失,第二项是采样的负样本作为输出单词的损失,注意sigmoid里面有个负号。上述损失非常像逻辑回归的损失(伯努利分布取对数得到的):
$$
E = - \sum_i \left(y_i log \sigma (x_i) + (1-y_i) log(1-\sigma(x_i) \right) \\
= - \sum_i \left(y_i log \sigma (x_i) + (1-y_i) log(\sigma(-x_i) \right)
$$
第一项是正样本的损失,第二项是负样本的损失。在逻辑回归中,对于某个训练样本,二者取其一。在word2vec,二者都取。第一项根据真实训练样本,第二项根据负采样样本。优化的目标是,最大化真实样本的概率$\sigma({\mathbf v_{w_O}^{\prime}}^T\mathbf h)$, 最小化负样本的概率$\sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h)$。
对于误差函数$E$,我们先求关于${\mathbf {v}^{\prime}_{w_j}}^T \mathbf h$的偏导数,得:
$$
\begin{align}
&\frac{\partial E}{\partial{ \mathbf v_{w_j}^{\prime}}^T\mathbf h}=
\begin{cases}
\sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h)-1 , &\text{if }\space w_j=w_O \\
\sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h), &\text {if}\space w_j\in W_{neg}
\end{cases}\tag{56}\\
&\space\space\space\space\space\space\space\space\space\space\space\space\space\space
=\sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h)-t_j \tag{57}
\end{align}
$$
其中,当$w_j$是一个正样本时,$t_j=1$;否则$t_j=0$。接下来我们计算E关于单词$w_j$的输出向量$v^{\prime}_{w_j}$的偏导数:
$$
\frac{\partial E}{\partial \mathbf v_{w_j}^{\prime}}=\frac{\partial E}{\partial {\mathbf v_{w_j}^{\prime}}^T\mathbf h}\cdot \frac{\partial {\mathbf v_{w_j}^{\prime}}^T\mathbf h}{\partial {\mathbf v_{w_j}^{\prime}}}=\Big(\sigma({\mathbf v_{w_j}^{\prime}}^T \mathbf h)-t_j\Big)\mathbf h \tag{58}
$$
因此输出向量的更新公式为:
$$
{\mathbf v_{w_j}^{\prime}}^{(new)}={\mathbf v_{w_j}^{\prime}}^{(old)}-\eta\Big(\sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h)-t_j\Big)\mathbf h\tag{59}
$$
上述优化公式和Hierarchical Softmax一样,只是$t_j$的含义不大一样。
对于某个训练样本,Negative Sampling的关键优化点在于公式(59)的更新过程只应用于词汇表的子集的输出向量,$\{w_j|w_j\in {w_O}\bigcup W_{neg}\}$。而并非应用于整个词汇表。通常负样本集合大小$k$取$log V$量级甚至更小。
回顾一下,Hierarchical Sampling 优化点在于,对于某个训练样本,优化输出向量时只优化路径上经过的$L(w)-1$个内部结点的输出向量。
- 接着利用反向传播机制,计算$E$关于隐藏层输出$h$的偏导数,$h$从1个正样本和负样本集合输出向量收集误差。
$$
\begin{align}
&\frac{\partial E}{\partial \mathbf h}=\sum_{w_j \in{w_O}\bigcup W_{neg}}\frac{\partial E}{\partial {\mathbf v_{w_j}^{\prime}}^T\mathbf h}\cdot \frac{\partial {\mathbf v_{w_j}^{\prime}}^T\mathbf h}{\partial \mathbf h}\tag{60}\\
&=\sum_{w_j \in{w_O}\bigcup W_{neg}}\Big(\sigma({\mathbf v_{w_j}^{\prime}}^T\mathbf h)-t_j\Big)\mathbf v_{w_j}^{\prime} \\
&= \sum_{w_j \in{w_O}\bigcup W_{neg}} e_j \cdot \mathbf v_{w_j}^{\prime}\\
&:= \mathbf{EH} \tag{61}
\end{align}
$$
上述公式和Hierarchical Softmax很像,只不过Hierarchical Softmax误差来源是$L(w)-1$个内部节点的输出向量,这里的误差来源是一个正样本以及负样本集合的输出向量。
接下来的过程和Hierarchical Softmax中一样。
将$\mathbf {EH}$代入公式22,我们就可以得到CBOW模型关于输入向量的更新公式:
$$
{\mathbf v_{W_{I,c}}}^{(new)}={\mathbf v_{W_{I,c}}}^{(old)}-\frac{1}{C} \cdot \eta \cdot \mathbf {EH}^T
$$
对于SG模型,我们需要计算上下文单词中的每个单词的$\mathbf{EH}$, 即,重复上述过程C次,每次得到一个$\mathbf {EH}$向量,最后将C个$\mathbf {EH}$累加,得到的向量作为该样本最终的$\mathbf {EH}$。代入公式33,这里再写一遍。
$$
{\mathbf v_{w_I}}^{(new)}={\mathbf v_{w_I}}^{(old)}-\eta \cdot \mathbf{EH}^T
$$
参考
word2vec Parameter Learning Explained
Distributed Representations of Words and Phrases and their Compositionality

