Attention in Deep Learning

目前深度学习中热点之一就是注意力机制（Attention Mechanisms）。Attention源于人类视觉系统，当人类观察外界事物的时候，一般不会把事物当成一个整体去看，往往倾向于根据需要选择性的去获取被观察事物的某些重要部分，比如我们看到一个人时，往往先Attend到这个人的脸，然后再把不同区域的信息组合起来，形成一个对被观察事物的整体印象。同理，Attention Mechanisms可以帮助模型对输入的每个部分赋予不同的权重，抽取出更加关键及重要的信息，使模型做出更加准确的判断，同时不会对模型的计算和存储带来更大的开销，这也是Attention Mechanism应用如此广泛的原因，尤其在Seq2Seq模型中应用广泛，如机器翻译、语音识别、图像释义（Image Caption）等领域。Attention既简单，又可以赋予模型更强的辨别能力，还可以用于解释神经网络模型（例如机器翻译中输入和输出文字对齐、图像释义中文字和图像不同区域的关联程度）等。本文主要围绕核心的Attention机制以及Attention的变体展开。

Seq2Seq Model

Attention主要应用于Seq2Seq模型，故首先简介一下Seq2Seq模型。Seq2Seq模型目标是学习一个输入序列到输出序列的映射函数。应用场景包括：机器翻译（Machine translation）、自动语音识别（Automatic speech recognition）、语音合成（Speech synthesis）和手写体生成（Handwriting generation）。

Seq2Seq模型奠基性的两个工作如下：

NIPS2014：Sequence to Sequence Learning with Neural Networks

该论文介绍了一种基于RNN(LSTM)的Seq2Seq模型，基于一个Encoder和一个Decoder来构建基于神经网络的End-to-End的机器翻译模型，其中，Encoder把输入编码成一个固定长度的上下文向量，Decoder基于上下文向量和目前已解码的输出，逐步得到完整的目标输出。这是一个经典的Seq2Seq的模型，但是却存在两个明显的问题：
- 把输入的所有信息有压缩到一个固定长度的隐向量，忽略了输入的长度，当输入句子长度很长，特别是比训练集中所有的句子长度还长时，模型的性能急剧下降（Decoder必须捕捉很多时间步之前的信息，虽然本文使用LSTM在一定程度上能够缓解这个问题）。
- 把输入编码成一个固定的长度过程中，对于句子中每个词都赋予相同的权重，这样做是不合理的。比如，在机器翻译里，输入的句子与输出句子之间，往往是输入一个或几个词对应于输出的一个或几个词。因此，对输入的每个词赋予相同权重，这样做没有区分度，往往使模型性能下降。
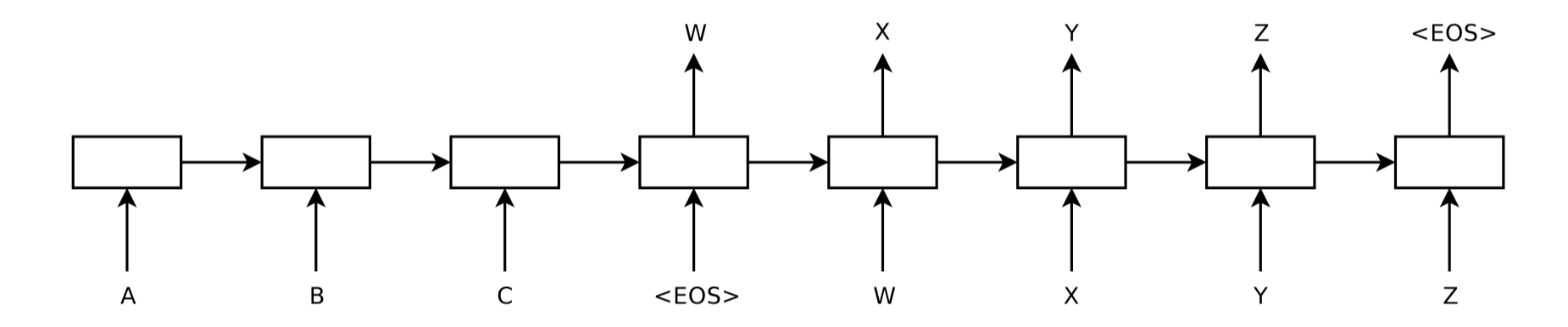
注意上图中Encoder得到的上下文向量仅用于作为Decoder的第一个时间步的输入。

Decoder的另一个输入是前一时刻的单词$\boldsymbol{y}_{t-1}$，需要注意的是，在训练阶段$\boldsymbol{y}_{t-1}$是真实label(需要embedding一下)，而不是上一时刻的预测值。而在测试阶段，则是上一时刻的预测值（具体使用时需要借助beam-search来得到最优翻译序列）。

但是实际训练过程中，label是否使用真实数据2种方式，可以交替进行，即一种是把标准答案作为Decoder的输入，还有一种是把Decoder上一次的输出的结果作为输入，因为如果完全使用标准答案，会导致收敛的过快，导致测试的时候不稳定。

另外，上述输入输出中的每个单词，都要借助embedding技术。
EMNLP2014：Learning Phrase Representations using RNN Encoder–Decoder for Statistical Machine Translation

和NIPS2014几乎同时发表，思想也是一样的。只不过在这篇文章中，作者提出了一种新的RNN Cell，即GRU代替LSTM来构建Seq2Seq模型。

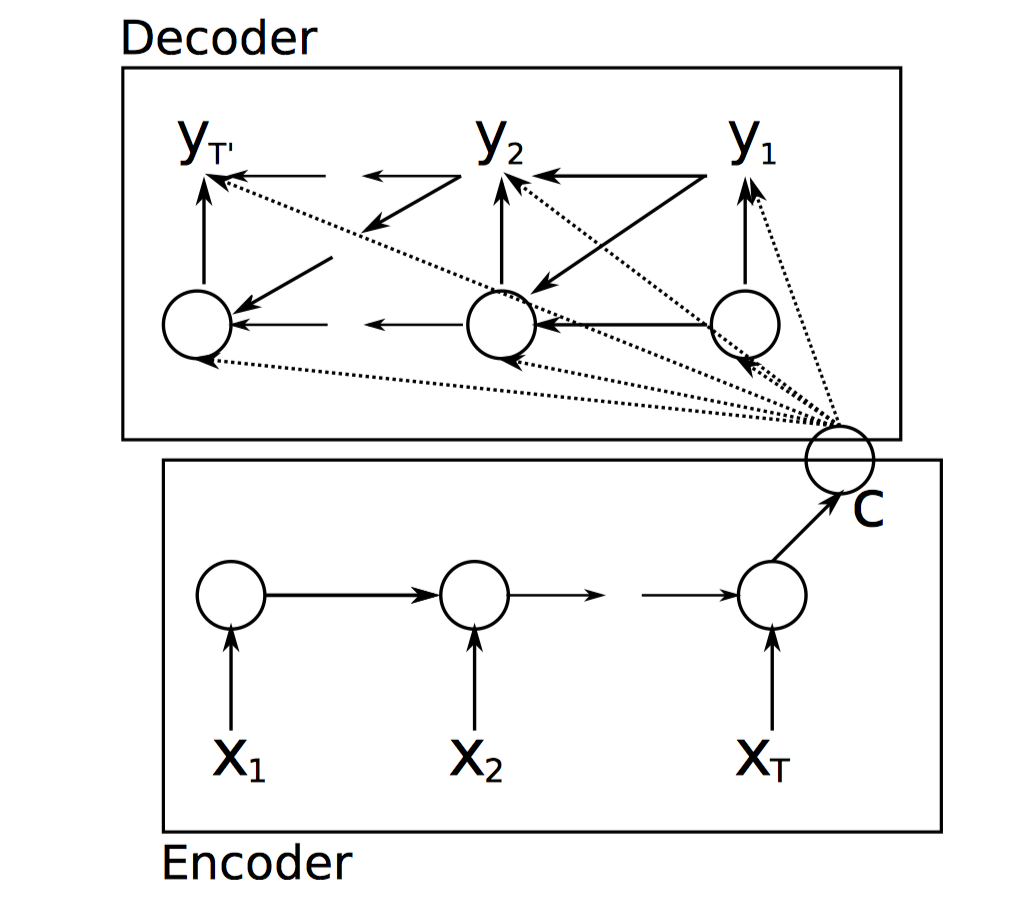
还有一点不同的是，Encoder得到的上下文向量会作用于Decoder每一个时间步的预测。

总结起来：RNN-based Encoder-Decoder Framework，目标是预测$P(\boldsymbol{y}_1,…,\boldsymbol{y}_{T_y}|\boldsymbol {x}_1,…,\boldsymbol{x}_{T_x})$，其中$\boldsymbol{y}_t, \boldsymbol{x}_s$都是one-hot向量。

Encoder：

给定输入，$x=(\boldsymbol{x}_1,…,\boldsymbol{x}_{T_x})$，将其编码为上下文向量$\boldsymbol {c}$.
$$
\boldsymbol{h}_t = f(\boldsymbol{W}\boldsymbol{x}_t, \boldsymbol{h}_{t-1})
$$
$f$是LSTM或GRU，$\boldsymbol{x}_t$是时间步$t$的单词的one-hot表示，先经过embedding矩阵$\boldsymbol{W}$嵌入后作为RNN在$t$时刻的输入，$\boldsymbol{h}_{t-1}$是$t-1$时间步的encode；$\boldsymbol{h}_t$是时间步$t$的encode。
$$
\boldsymbol{c} = q(\{\boldsymbol{h}_1, …, \boldsymbol{h}_{T_x}\})
$$
$c$是上下文向量，是关于$\{\boldsymbol{h}_1, …, \boldsymbol{h}_{T_x}\}$的函数。$T_x$是输入的最大长度。最简单的，$q(\{\boldsymbol{h}_1, …, \boldsymbol{h}_{T_x}\})=\boldsymbol{h}_T$，即最后一个时间步得到的encode作为上下文向量。

Decoder

Decoder在给定上下文向量$\boldsymbol{c}$以及已经预测的输出$\{\boldsymbol{y}_1,…,\boldsymbol{y}_{t^{\prime}-1}\}$条件下，预测下一个输出$\boldsymbol{y}_{t^{\prime}}$。换句话说，Decoder将输出$\boldsymbol{y}$上的联合分布分解为有序条件分布 (ordered conditionals)：
$$
p(\boldsymbol{y})=\prod_{t=1}^{T_{y}} p(\boldsymbol{y}_t|\{\boldsymbol{y}_1,…,\boldsymbol{y}_{t-1}\}, \boldsymbol{c})
$$
其中，$\boldsymbol{y}=\{\boldsymbol{y}_1,…,\boldsymbol{y}_{T_y}\}$，$T_y$是输出的最大长度。

使用RNN，每个条件分布可以写成下式：
$$
p(\boldsymbol{y}_t|\{\boldsymbol{y}_1,…,\boldsymbol{y}_{t-1}\}, \boldsymbol{c})=g(\boldsymbol{E}\boldsymbol{y}_{t-1},\boldsymbol{s}_t,\boldsymbol{c})
$$
$\boldsymbol{y}_t$是输出词的one-hot向量(全连接+softmax激活后得到)，$\boldsymbol{y}_{t-1}$是前一时刻已经预测的输出词的one-hot向量，先经过$\boldsymbol{E}y_{t-1}$embedding后再作为$g$的输入。$g$是一个非线性函数(e.g., 全连接+softmax)，输出关于$\boldsymbol{y}_t$的概率分布。$\boldsymbol{s}_t$（$\boldsymbol{s}_t=f(\boldsymbol{E} \boldsymbol{y}_{t-1}, \boldsymbol{s}_{t-1},\boldsymbol{c})$，$f$是LSTM/GRU）是RNN的隐藏层状态。（注意，$g$不是RNN提取隐藏层状态的LSTM或GRU，而是隐藏层后面接的全连接层或其他非线性函数，LSTM或GRU提取的Decoder隐状态和上下文向量以及已经预测的输出都将作为$g$的输入，用于预测概率分布）。

Attention

如上文所述，传统的Seq2Seq模型对输入序列缺乏区分度，存在明显的两大问题。因此，有大牛提出使用Attention机制来解决问题。下面将按照Attention的不同类型重点介绍一些Attention上的研究工作。

Basic Attention

本小节介绍最传统和基础的Attention模型的应用。首先直观感受下Attention机制的一个示意动图。

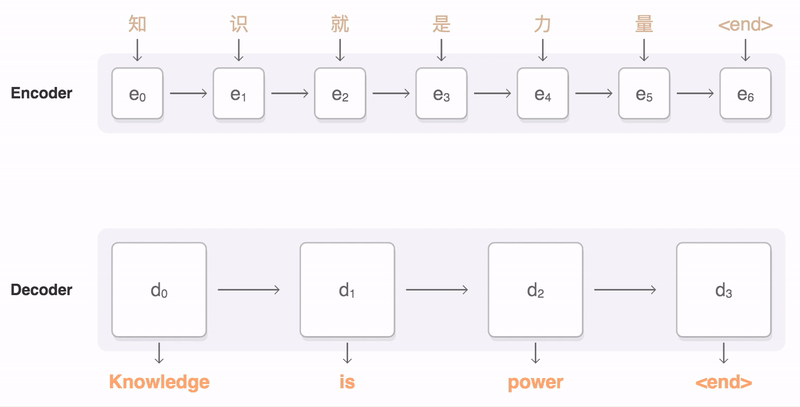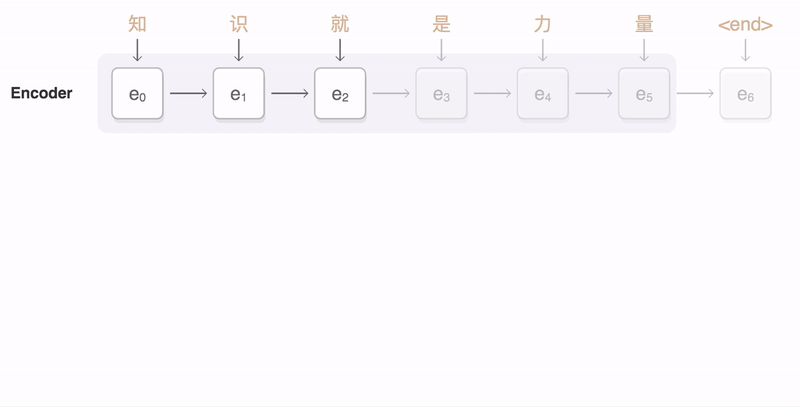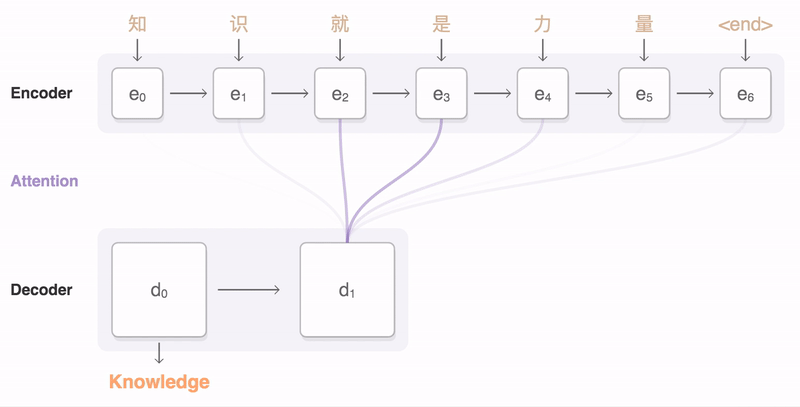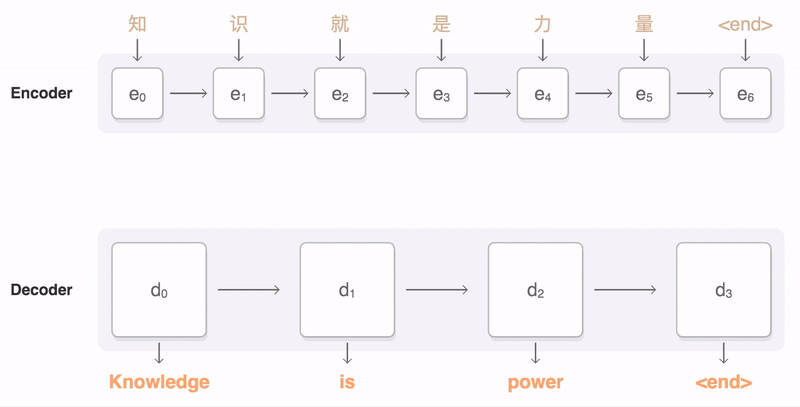
Machine Translation

ICLR2015: Neural Machine Translation by Jointly Learning to Align and Translate

这是ICLR2015提出的文章，机器翻译的典型方法。作者在RNN Encoder-Decoder框架上，引入了Attention机制来同时进行翻译和对齐。使用bidirectional RNN作为Encoder，Decoder会在翻译的过程中通过模拟搜索源句子focus到不同部位上来进行更准确的解码。模型示意图如下：

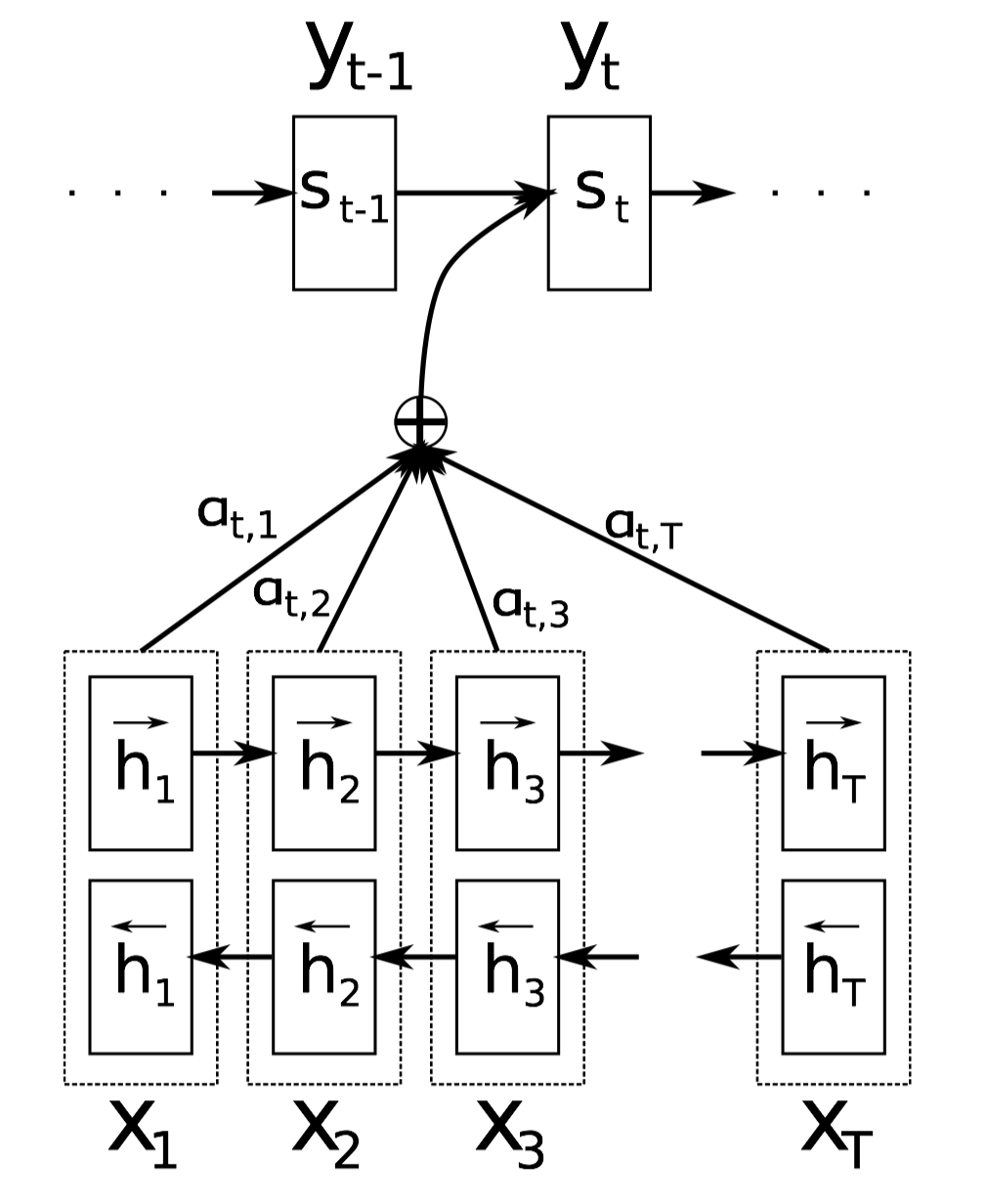
首先将Decoder中的条件概率写成下式：
$$
p(\boldsymbol{y}_t|\{\boldsymbol{y}_1,…,\boldsymbol{y}_{t-1}\}, \boldsymbol{x})=g(\boldsymbol{E}\boldsymbol{y}_{t-1},\boldsymbol{s}_t,\boldsymbol{c}_t)
$$
其中，$g$一般使用softmax全连接层（或多加几层，输入的3个向量concat到一起后进行Feed Forward），$\boldsymbol{s}_i$是Decoder中RNN在时间步$t$的隐状态，根据如下LSTM或GRU函数计算得到：
$$
\boldsymbol{s}_t=f(\boldsymbol{s}_{t-1},\boldsymbol{E} \boldsymbol{y}_{t-1}, \boldsymbol{c}_t)
$$
$\boldsymbol{s}_{t}$是关于前一时刻Decoder端隐状态$\boldsymbol{s}_{t-1}$，前一时刻已经预测的输出$\boldsymbol{y}_{t-1}$的embedding表示$\boldsymbol{E} \boldsymbol{y}_{t-1}$以及该时刻$t$的上下文向量$\boldsymbol{c}_t$的函数。$f$是LSTM或GRU。

注意，和已有的encoder-decoder不同，这里的条件概率对每一个目标单词$t$都需要有一个不同的上下文向量$\boldsymbol{c}_t$。

而上下文向量$\boldsymbol{c}_t$取决于Encoder端输入序列encode后的RNN隐状态$\boldsymbol{h}_s$(bidirectional RNN，因此$\boldsymbol{h}_s$包含了输入句子$s$位置周围的信息，有，$\boldsymbol{h}_s=[\overleftarrow{\boldsymbol{h}}_s^T; \overrightarrow{\boldsymbol{h}}_s^T]$)
$$
\boldsymbol{c}_t = \sum_{s=1}^{T_x} \alpha_{ts} \boldsymbol{h}_s
$$
而每一个权重$\alpha_{ts}$使用softmax转换为概率分布：
$$
\alpha_{ts} = \frac{\exp(e_{ts})}{\sum_{k=1}^{T_x} (e_{tk})}
$$
而$e_{ts}$是输出$t$和输入$s$的对齐模型(alignment model)，衡量了输入位置$s$周围的信息和输出位置$t$的匹配程度。
$$
e_{ts}=a(\boldsymbol{s}_{t-1}, \boldsymbol{h}_s)
$$
$e_{ts}$得分依赖于Decoder端$t$时刻的前一时刻的隐状态$s_{t-1}$和Encoder端$s$时刻的隐状态。文中使用前馈神经网络学习对齐模型，并且和其他组件联合学习，$a$实际上学到的是soft alignment，因此可以很容易应用梯度反向传播。

总之，$\alpha_{ts}$可以理解为衡量了输出单词$t$和输入单词$s$的对齐程度，而$\boldsymbol{c}_t$是$t$时刻，所有encode隐状态根据该对齐程度得到的期望上下文向量，是所有对齐情况下的期望。$\alpha_{ts}$衡量了在计算下一个decoder隐状态$s_t$和预测$y_t$过程中，相对于前一个decoder隐状态$\boldsymbol{s}_{t-1}$，不同$\boldsymbol{h}_s$的重要性程度。这一Decoder中的注意力机制使得只需要关注源句子部分的信息，而不是像此前工作中非要将源句子所有的信息都编码成固定长度的上下文向量来用。

Image Caption

ICML2015: Show, Attend and Tell- Neural Image Caption Generation with Visual Attention

Kelvin Xu等人在该论文中将Attention引入到Image Caption中。Image Caption是一种场景理解的问题，这是视觉领域重要的一个研究方向。场景理解的难点在于既要进行物体识别，又要理解物体之间的关系。这相当于要让机器拥有模仿人类将大量显著的视觉信息压缩为描述性语言的能力。

模型包括两个部分：Encoder和Decoder。其中，Encoder会使用CNN提取图片低层特征；Decoder会在RNN中引入注意力机制，将图片特征解码为自然语言语句。模型总的示意图如下：

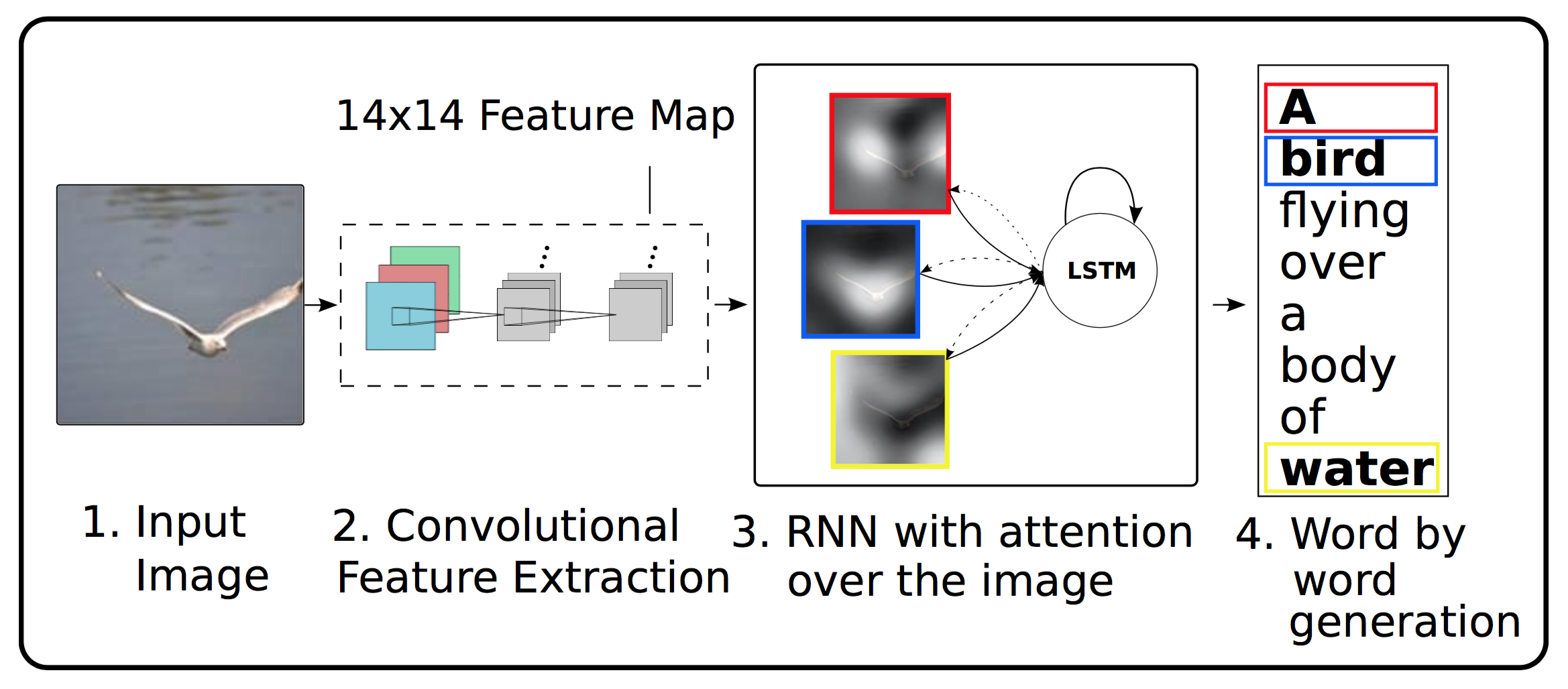
如上图，模型把图片经过CNN网络，变成特征图。 LSTM的RNN结构在此上运行Attention模型，最后得到描述。

目标：输入一个图像，输出该图像的描述$y=\{\boldsymbol{y}_1,…,\boldsymbol{y}_C \}, y_i \in \mathbb{R}^K$，其中$K$是词典词汇的数量，$\boldsymbol{y}_i$是词的one-hot表示向量，$C$是描述的长度。

Encoder:

在encoder端，模型使用CNN来提取L个D维vector，每一个都对应图像的一个区域(这里粗体表示向量)：
$$
a = \{ \boldsymbol{a}_1, \dots, \boldsymbol{a}_L \}, a_i \in \mathbb{R}^D
$$
在原论文中，原始图像先经过center cropped变为$224\times224$的图像，然后经过卷积和pooling操作，共4次max pooling，最后得到$14 \times 14$的feature map，feature map个数共512个，即512个通道。这里$L=14 \times 14=196$对应的就是196个区域数量，每个区域都是原始图像经过下采样得到的，因此可以通过4次上采样能够恢复原始图像中对应区域。而$D=512$，即每个区域的向量化表示是由所有的feature map相应位置数值构造而成。

与此前的工作使用Softmax层之前的那一层vector作为图像特征不同，本文所提取的这些vector来自于 low-level 的卷积层，这使得Decoder可以通过从所有提取到的特征集中，选择一个子集来聚焦于图像的某些部分。这样子就有点像NLP里的seq2seq任务了，这里的输入从词序列转变成了图像区域vector的序列。作为类比，图像上的$L$个区域($14 \times 14$平展开为196)就相当于句子的长度（单词的数量$T_x$）；每个区域的D维向量化表示是由D个Filter提取的该区域的特征concat在一起形成的向量，类比于句子每个单词的embedding经过RNN提取的隐状态向量。

上下文向量$\hat{\boldsymbol{z}}_t$计算如下：
$$
\hat{\boldsymbol{z}}_t = \phi(\{\boldsymbol{a}_i\},\{\alpha_i\})
$$
即，在给定一组提取到的图像不同区域的向量表示$\{\boldsymbol {a_i}\}$，以及不同区域相应的权重$\{\alpha_i\}$条件下，计算上下文向量，最简单的方式是使用上文所述的加权和来处理。本文使用了两种Attention Mechanisms，即Soft Attention和Hard Attention。我们之前所描述的传统的Attention Mechanism就是Soft Attention。Soft Attention是参数化的（Parameterization），因此可导，可以被嵌入到模型中去，直接训练，梯度可以经过Attention Mechanism模块，反向传播到模型其他部分。相反，Hard Attention是一个随机的过程，根据$\{\alpha_i\}$随机采样。Hard Attention不会选择整个encoder的输出做为其输入，Hard Attention会依概率来采样输入端的隐状态一部分来进行计算，而不是整个encoder的隐状态。为了实现梯度的反向传播，需要采用蒙特卡洛采样的方法来估计模块的梯度。

而权重$\alpha_i$的计算，作者引入了一个Attention模型，实际上就是上篇文章MT任务中的对齐模型。
$$
e_{ti}=f_{att}(\boldsymbol{a}_i, \boldsymbol{h}_{t-1})
$$
$t$是当前要预测的输出词的位置，$i$是输入词的位置。
$$
\alpha_{ti}=\frac{exp(e_{ti})}{\sum_{k=1}^{L} (e_{tk})}
$$
Decoder:

使用LSTM来解码并生成描述词序列，LSTM结构单元如下：

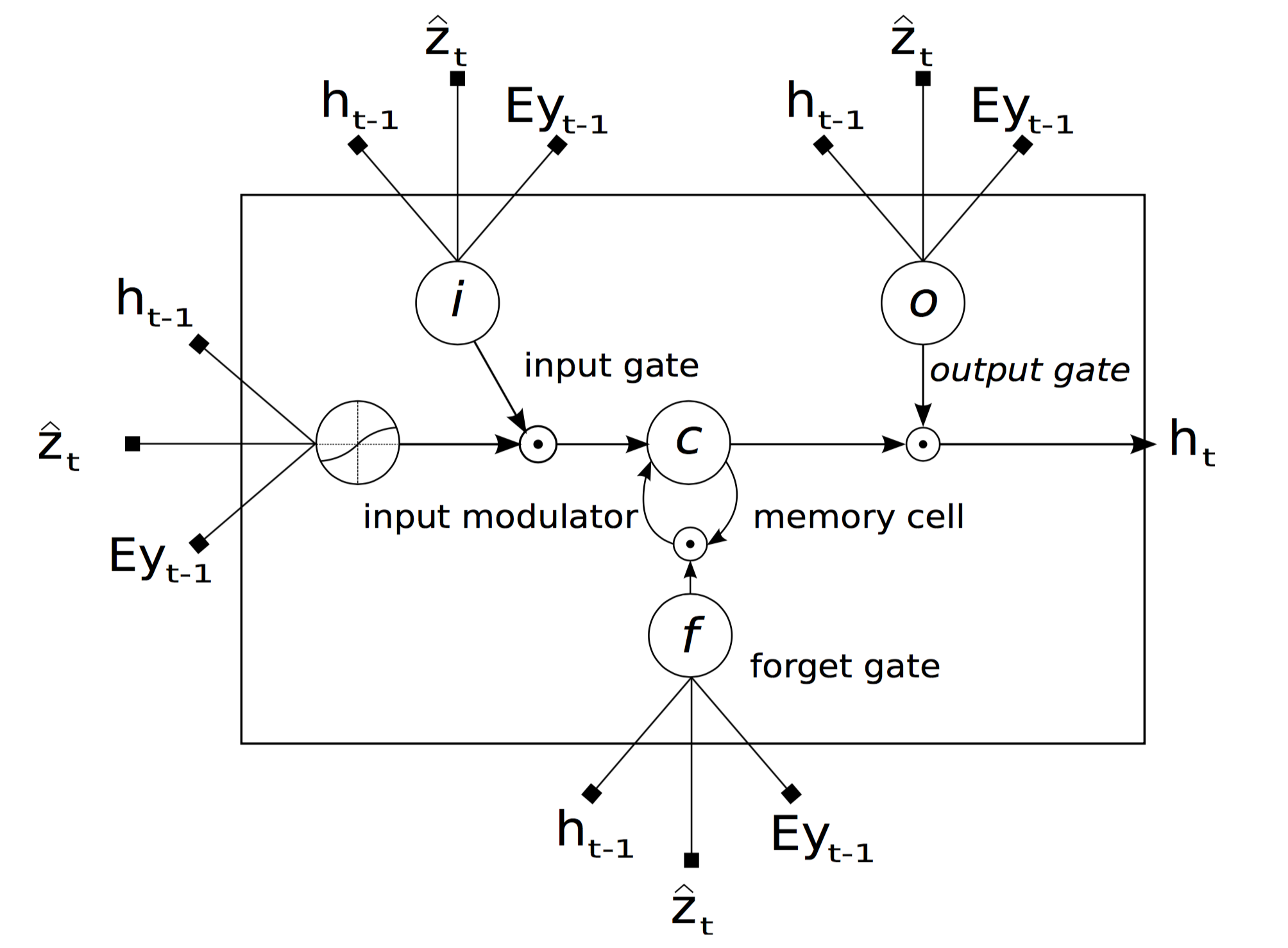
具体LSTM的计算：(可以发现如何将$\hat{z}_t$融入到LSTM中的，实际上就是多一个线性变换，再全部加起来)
$$
\begin{pmatrix}
\mathbf{i}_t \\
\mathbf{f}_t \\
\mathbf{o}_t \\
\mathbf{g}_t \\
\end{pmatrix}
=
\begin{pmatrix}
\sigma \\
\sigma \\
\sigma \\
\tanh \\
\end{pmatrix}
\mathbf{T}_{D+m+n, n}
\begin{pmatrix}
\mathbf{E} \mathbf{y}_{t-1} \\
\mathbf{h}_{t-1} \\
\hat{\mathbf{z}}_t \\
\end{pmatrix}
$$

$$
\mathbf{c}_t = \mathbf{f}_t \odot \mathbf{c}_{t-1} + \mathbf{i}_t \odot \mathbf{g}_t
$$

$$
\mathbf{h}_t = \mathbf{o}_t \odot \tanh(\mathbf{c}_t)
$$

第一个式子实际上是四个式子，分别得到输入门、遗忘门、输出门和被输入门控制的候选向量。其中，三个门控由sigmoid激活，得到的是元素值皆在 0 到 1 之间的向量，可以将门控的值视作保留概率；候选向量由tanh激活，得到的是元素值皆在－1到1之间的向量。$\boldsymbol{T}_{s,t}: \mathbb{R}^s \rightarrow \mathbb{R}^t$是仿射变换，在上式也就是要对最右边的三项进行加权求和，可以将T理解为分块矩阵。最右边的三个式子，其中$\boldsymbol{E} \in \mathbb{R}^{m\times K}$是输出词的embedding matrix，$\boldsymbol{y}_{t-1}$是one-hot词表示，$\boldsymbol{E}\boldsymbol{y}_{t-1}$用来lookup，得到dense词向量表示。$\boldsymbol{h}_{t-1} \in \mathbb{R}^n$是前一时刻的decoder状态，$\boldsymbol{\hat{z}}_t \in \mathbb{R}^D$是LSTM真正意义上的“输入”，代表的是捕捉了特定区域视觉信息的上下文向量，既然它和时刻$t$有关，就说明它是一个动态变化的量，在不同的时刻将会捕捉到与本时刻相对应的相关图像区域。这个量将由attention机制计算。

第二个式子是更新旧的记忆单元，element-wise 的运算表示三个门控将对各自控制的向量的每个元素做“取舍”：0 到 1 分别代表完全抛弃到完全保留。第三个式子是得到隐状态。

有了隐状态，就可以计算词表中各个词的概率值，那么取概率最大的那个作为当前时刻生成的词，并将作为下一时刻的输入。其实就是softmax全连接层(两层MLPs+softmax)。$K$是单词的数量。
$$
p(\mathbf{y}_t \mid \mathbf{a}, \mathbf{y}_{t-1}) \propto \exp (\mathbf{L}_o (\mathbf{E} \mathbf{y}_{t-1} + \mathbf{L}_h \mathbf{h}_t + \mathbf{L}_z \hat{\mathbf{z}}_t)) \\
\mathbf{L}_o \in \mathbb{R}^{K \times m} \\
\mathbf{L}_h \in \mathbb{R}^{m \times n} \\
\mathbf{L}_z \in \mathbb{R}^{m \times D}
$$
原论文中还有一些比较有意思的Trick。

解码的输出：

模型生成的一句caption被表示为各个词的one-hot编码所构成的集合，输出的caption y表示为：

$$
y = \{ \mathbf{y}_1, \dots, \mathbf{y}_C \}, y_i \in \mathbb{R}^K
$$

$K$是字典的单词个数，$C$是句子长度。 $\boldsymbol{y}_i$的形式为$(0,0,…,0,1,0,…,0,0)$，即只有第$i$处位置为1，其它位置为0。

RNN建模时，$\boldsymbol{y}_i$会用在embedding，将稀疏one-hot向量转成dense的embedding向量。模型的输出概率$p(\mathbf{y}_t \mid \mathbf{a}, \mathbf{y}_{t-1})$会用于拟合真实的$\boldsymbol{y}_t$。

LSTM初始输入：

LSTM中的记忆单元与隐藏单元的初始值，是两个不同的多层感知机，采用所有特征区域的平均值来进行预测的:
$$
\mathbf{c}_0 = f_{\mathbf{init,c}}({1 \over L} \sum_i^L \mathbf{a}_i) \\
\mathbf{h}_0 = f_{\mathbf{init,h}}({1 \over L} \sum_i^L \mathbf{a}_i)
$$

图像的encode：

文中使用VGGnet作为encoder进行编码，且不进行finetuning。encoder得到$14 \times 14 \times 512$的feature maps。因此decoder处理的是flattened$196 \times 512$ ($i.e. L \times D$)。
Caption的Decode：

在decode时，由于模型每次更新所需要的时间正比于最长的句子，如果随机采样句子进行解码，训练时间会很长。为了解决这个问题，文中会在预处理环节，将句子按照长度分组。每次更新时，随机采样一个长度，然后使用相应的分组内的句子进行训练，这样就能显著提高运行效率。

个人觉得输出词的embedding matrix也可以使用word2vec预训练好的词向量代替，文中没提到。

Speech Recognition

NIPS2015: Attention-Based Models for Speech Recognition

给定一个英文的语音片段作为输入，输出对应的音素序列。Attention机制被用于对输出序列的每个音素和输入语音序列中一些特定帧进行关联。

Entailment

ICLR2016: Reasoning about Entailment with Neural Attention

语义蕴含，句子关系推断方面的早期工作，也是采用了基本的Attention模型。给定一个用英文描述的前提和假设作为输入，输出假设与前提是否矛盾、是否相关或者是否成立。举个例子：前提：在一个婚礼派对上拍照；假设：有人结婚了。该例子中的假设是成立的。Attention机制被用于关联假设和前提描述文本之间词与词的关系。

Text Summarization

EMNLP2015: A Neural Attention Model for Sentence Summarization

给定一篇英文文章作为输入序列，输出一个对应的摘要序列。Attention机制被用于关联输出摘要中的每个词和输入中的一些特定词。

Attention Variants

本部分介绍Attention机制的各种变体。包括但不限于：

基于强化学习的注意力机制：选择性的Attend输入的某个部分
全局&局部注意力机制：其中，局部注意力机制可以选择性的Attend输入的某些部分
多维度注意力机制：捕获不同特征空间中的Attention特征。
多源注意力机制：Attend到多种源语言语句
层次化注意力机制：word->sentence->document
注意力之上嵌一个注意力：和层次化Attention有点像。
多跳注意力机制：和前面两种有点像，但是做法不太一样。且借助残差连接等机制，可以使用更深的网络构造多跳Attention。使得模型在得到下一个注意力时，能够考虑到之前的已经注意过的词。
使用拷贝机制的注意力机制：在生成式Attention基础上，添加具备拷贝输入源语句某部分子序列的能力。
基于记忆的注意力机制：把Attention抽象成Query，Key，Value三者之间的交互；引入先验构造记忆库。
自注意力机制：自己和自己做attention，使得每个位置的词都有全局的语义信息，有利于建立长依赖关系。

Reinforcement-learning based Attention

NIPS2014: Recurrent Models of Visual Attention

ICLR2015: Multiple Object Recognition with Visual Attention

NIPS2014论文应该是最早的Attention雏形，虽然和我们通常所说的、广泛应用于Seq2Seq的Attention机制不太一样，但是还是值得提一下。这是Google DeepMind2014年提出的一篇计算机视觉领域的文章，适用于处理图像序列或帧序列来进行场景感知或处理（例如Video Caption）。其动机在于随着分辨率提高，计算量不断增长，神经网络难以在实时应用场景中，快速处理这么大的计算量。借鉴人类视觉系统的特点，即，为了理解某个场景，并不是一下子处理整个场景，而是Focus到某些关键的位置上，然后联合起来构建出整个场景信息。故本篇论文利用RNN处理图像序列，并使用强化学习来训练模型，使得模型能够学习attention决策。即，针对实时的场景，基于过去的信息和任务的需要选择下一个要focus的感知区域。这个和人类的感知方式比较相似，也是我们最早理解的Attention机制。

但是，上文所述的广泛应用于Seq2Seq中的Attention不大一样。人类的注意力机制实际上是可以节省计算资源的，注意只需要集中到某些区域，可以忽略大部分区域。Recurrent Models of Visual Attention中的做法和这个是一样的。然而，下文即将要介绍的应用于Seq2Seq模型模型的Attention就不是这样的了。实际上，下文所述Attention模型，需要把每一个部分都观察的仔仔细细(每部分权重都要算一下)，才能进一步决策到底需要focus到哪些部分，这和人类的视觉系统不相符，更像是memory，而不是attention（实际上attention可以理解为一种短期记忆，即根据短期记忆在输入特征上分配attention；memory也是另外一种非常重要的机制），然而，这并不妨碍注意力机制的有效性。

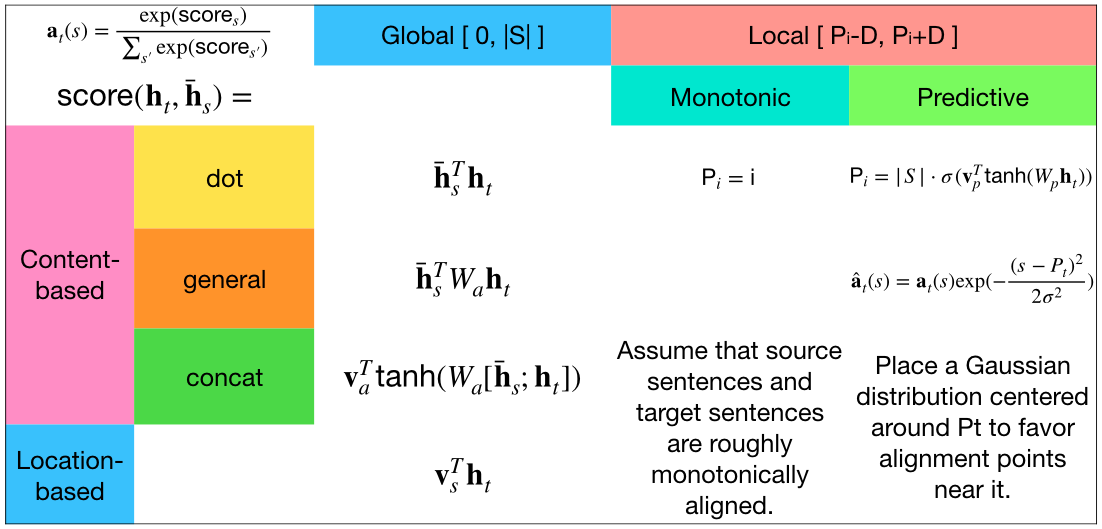
Global & Local Attention

EMNLP2015: Effective Approaches to Attention-based Neural Machine Translation

以往的文章，主要将attention应用于不同场景中，而这篇文章提出了新的attention架构，引入了Global Attention和Local Attention的概念。Global Attention和上文的Soft Attention几乎一样，即计算上下文向量时，和所有的encoder隐状态向量求alignment；而Local Attention是Soft Attention和Hard Attention的权衡，既拥有Soft Attention可微分，容易使用反向传播来优化的优点，又拥有Hard Attention复杂度低的优点，除此之外，还不需要强化学习方法进行训练。

首先定义，Encoder得到的源语句单词$s$的隐状态为：$\boldsymbol{\bar{h}}_s$；Decoder中目标语句单词$t$的隐状态为：$\boldsymbol{h}_t$；对每一个目标单词$t$，使用Attention机制计算的上下文向量为$\boldsymbol{c}_t$；Attention机制中的对齐模型为$\boldsymbol{a}_t=f(\{\boldsymbol{\bar{h}_s}\}, \boldsymbol{h_t})$（前面文章中都是使用$\boldsymbol{h}_{t-1}$, 即前一个时间步的Decoder隐状态和Encoder隐状态来计算对齐权重）。

首先是Global Attention，如下图所示：

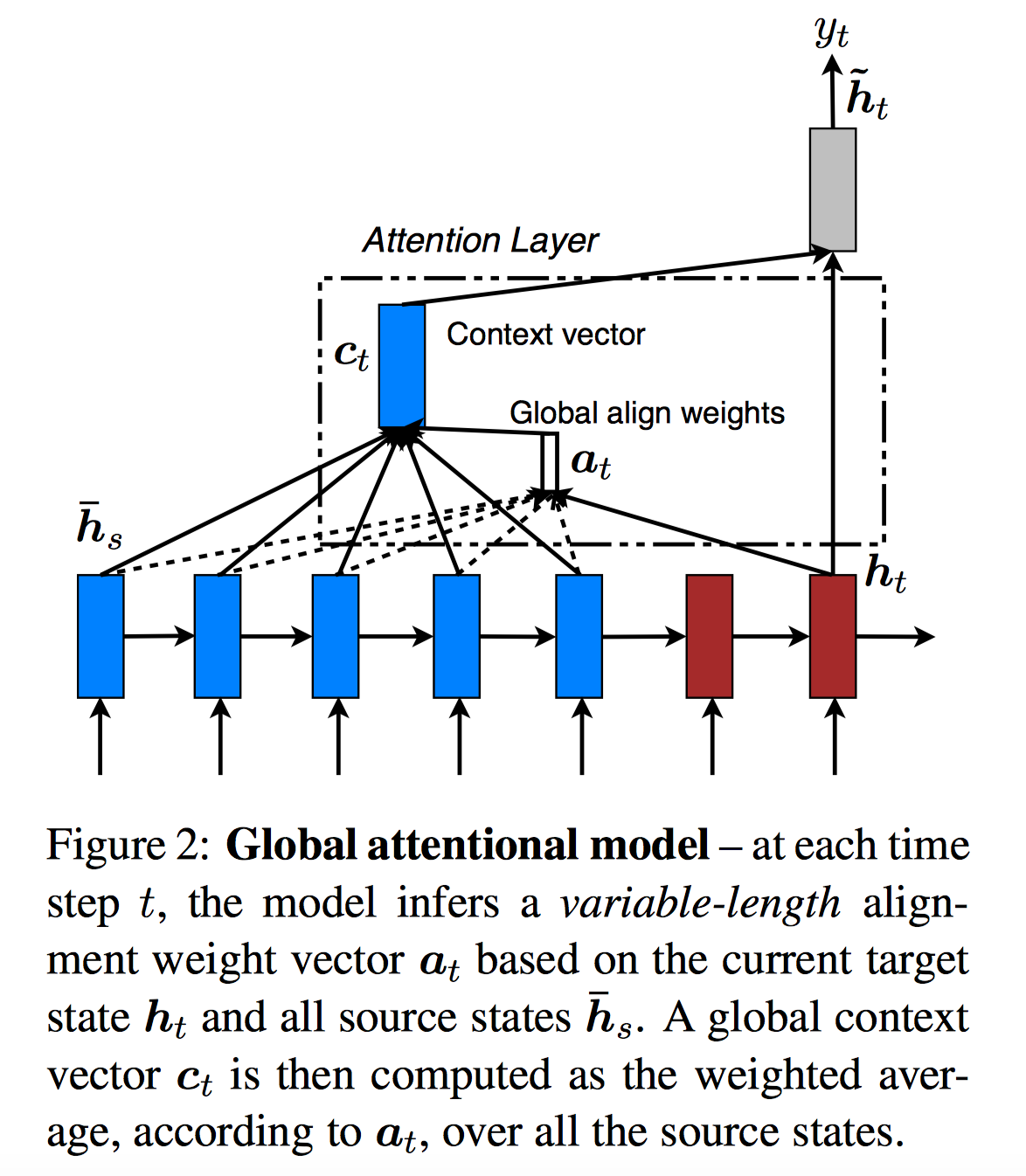
Global Attention中上下文向量$\boldsymbol{c}_t$的计算路径为：$\boldsymbol{h}_t \rightarrow \boldsymbol{a_t} \rightarrow \boldsymbol{c}_t$。

对齐模型计算：
$$
\boldsymbol{a}_t(s)=\text{align}(\boldsymbol{h}_t, \boldsymbol{\bar{h}_s})=\frac{\exp(\text{score}(\boldsymbol{h}_t, \boldsymbol{\bar{h}}_s))}{\sum_{s^{\prime}}\exp(\text{score}(\boldsymbol{h}_t, \boldsymbol{\bar{h}}_{s^{\prime}}))}
$$
$s$是源语句单词的位置。

$\text{score}$具体可以采用：
$$
\begin{equation}
\text{score}(\boldsymbol{h}_t, \boldsymbol{\bar{h}}_s) = \left\{
\begin{aligned}
\boldsymbol{h}_t^T \boldsymbol{\bar{h}}_s &, & \text{dot} \\
\boldsymbol{h_t}^T \boldsymbol{W}_{\alpha}\boldsymbol{\boldsymbol{\bar{h}}}_s &, & \text{general} \\
\boldsymbol{v_a}^T \tanh(\boldsymbol{W}_{\alpha}[\boldsymbol{h_t}; \boldsymbol{\bar{h}}_s]) &, & \text{concat}
\end{aligned}
\right.
\end{equation}
$$
上下文向量计算：
$$
\boldsymbol{c}_t = \sum_{s=1}^{S} a_{ts} \boldsymbol{\bar{h}}_s
$$
注意图中，框起来的部分作者称为Attention Layer。

接着是Local Attention，如下图所示：

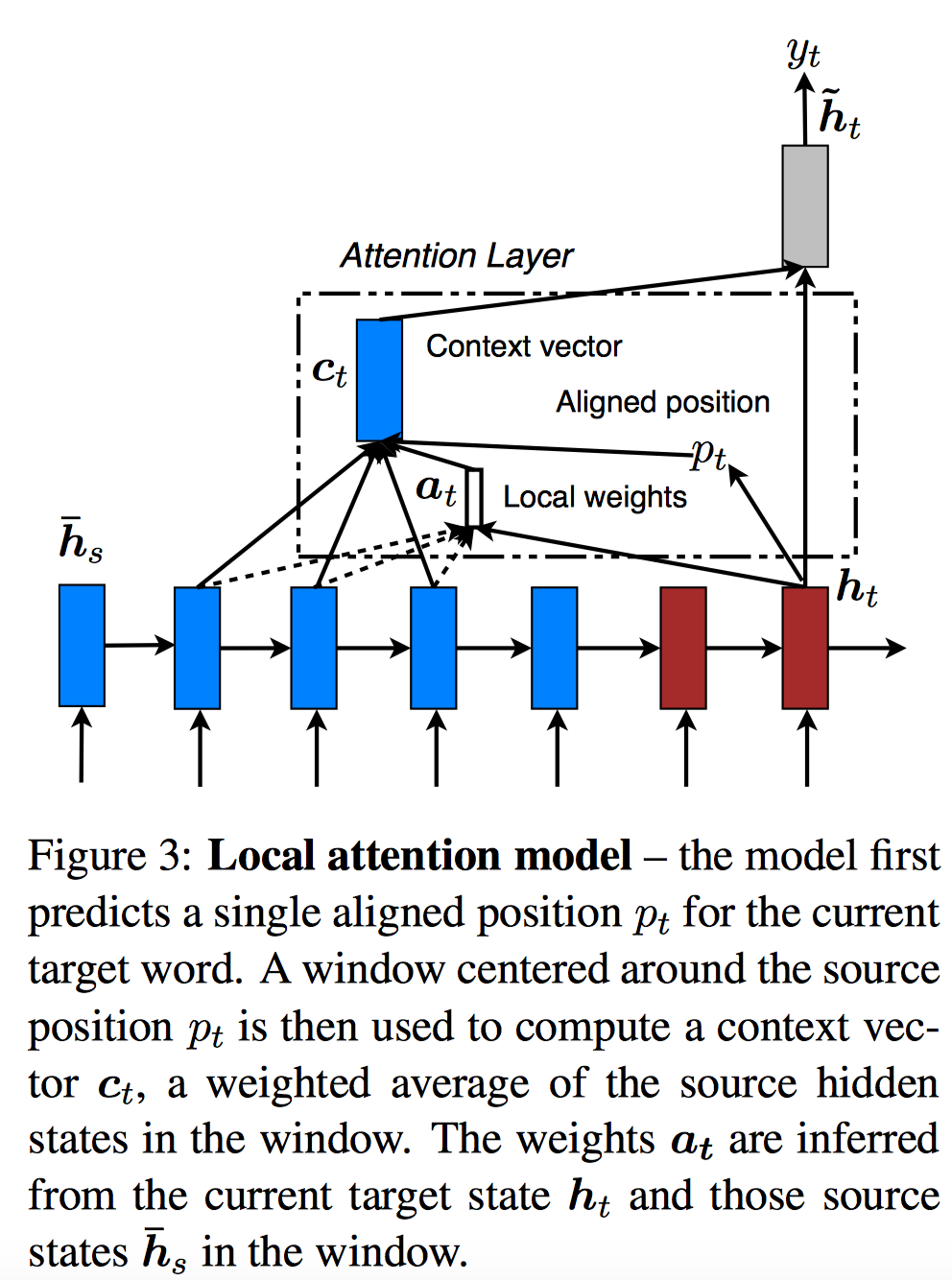
Local Attention的引入是为了解决Global Attention中Attend到源语句中所有的词，一方面复杂度高，另一方面很难翻译长序列语句。Local Attention首先根据目标词的隐状态$\boldsymbol{h}_t$计算源语句中的对齐位置（中心）$p_t$，然后使用以该位置为中心的窗口$[p_t-D, p_t+D]$内的源语句单词$\boldsymbol{\bar{h}_s}$，来计算Attention的权重，计算时使用以$p_t$为中心的高斯核函数进行衰减。具体如下：

对齐位置模型：$p_t = S \cdot \text{Sigmoid}(\boldsymbol{v}_p^T \tanh(\boldsymbol{W}_p \boldsymbol{h}_t))$， $p_t \in [0, S]$， $S$是源语句长度。只与t时刻Decoder状态$\boldsymbol{h}_t$有关。
对齐权重模型：$\boldsymbol{a}_t(s)=\text{align}(\boldsymbol{h}_t, \boldsymbol{\bar{h}}_s)\exp(-\frac{(s-p_t)^2}{2\sigma^2})$，也就是在global Attention对齐模型基础上加了高斯函数指数衰减。$s \in [p_t-D, p_t + D]$。

计算上下文向量时，同上文，即对窗口内的encoder隐向量进行加权，即$\boldsymbol{c}_t = \sum_{s=1}^{S} a_{ts} \boldsymbol{\bar{h}}_s$。

计算得到上下文向量后，本文直接将$\boldsymbol{c}_t$和$\boldsymbol{h}_t$ concat在一起，并计算经过attention后的隐状态$\boldsymbol{\tilde{h}}_t$：
$$
\boldsymbol{\tilde{h}}_t = \tanh(\boldsymbol{W}_c[\boldsymbol{c}_t, \boldsymbol{h}_t])
$$
再将上述attention后的隐状态输入到一个softmax全连接层，得到预测目标值：
$$
p(y_t |y_{<t}, x) = \text{softmax}(\boldsymbol{W}_s \boldsymbol{\tilde{h}}_t)
$$
按照上述方式来看，每个目标输出单词的预测值，没有利用已经预测的输出单词(embedding)作为输入，也没有利用目标词位置前一时刻的decoder隐状态$\boldsymbol{h}_{t-1}$；只利用了当前时刻Decoder隐状态$\boldsymbol{h}_t$（上下文向量计算中的权重也主要依据这个计算的）。也就是说，每个目标词位置的attention决策是独立的（只和$h_t$本身相关）。

然而在机器翻译当中，通常要维护一个覆盖集，即源语句中哪些单词被翻译过了；同理，在神经机器翻译中，我们在翻译一个目标词时，同样需要关注哪些源语句单词已经被翻译了。因此，作者提出了一个Input-feeding approach，把Decoder端前一时刻attention后的隐状态和前一时刻预测的输出单词的embedding连接起来，作为下一时刻的输入。（这个和传统Attention的几乎没差别）

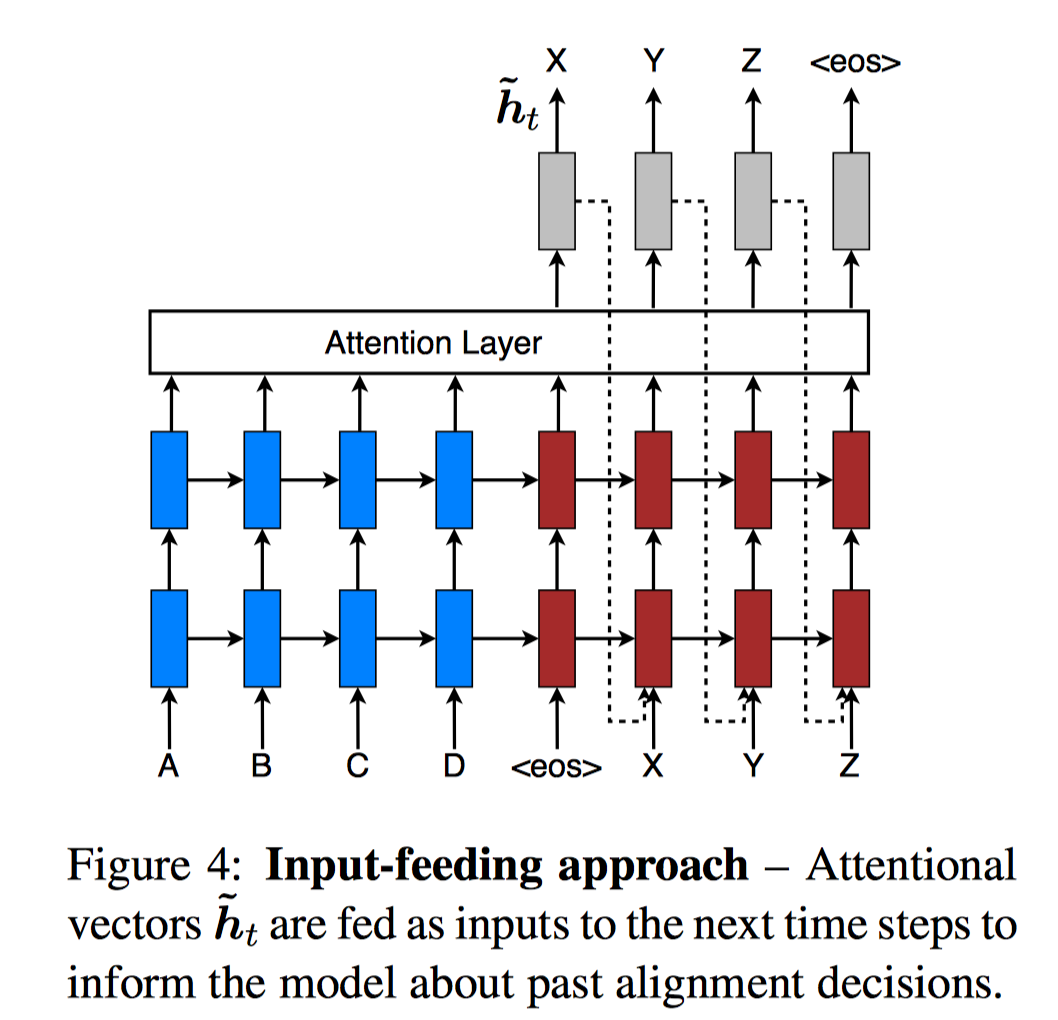
本文的贡献主要是Local Attention以及提出的各种各样的Alignment函数，其余都和前面的工作大同小异。现总结下Alignment函数如下图所示：

Multi-dimensional Attention

AAAI2018：DiSAN: Directional Self-Attention Network for RNN/CNN-Free Language Understanding

在Baisc Attention中，对于每个查询，每个key对应的value都有一个权重值，即每个查询会对应一个1-D的Attention weight向量。而Multi-dimensional Attention会产生更高维度的Attention矩阵，旨在捕获不同特征空间中的Attention特征。

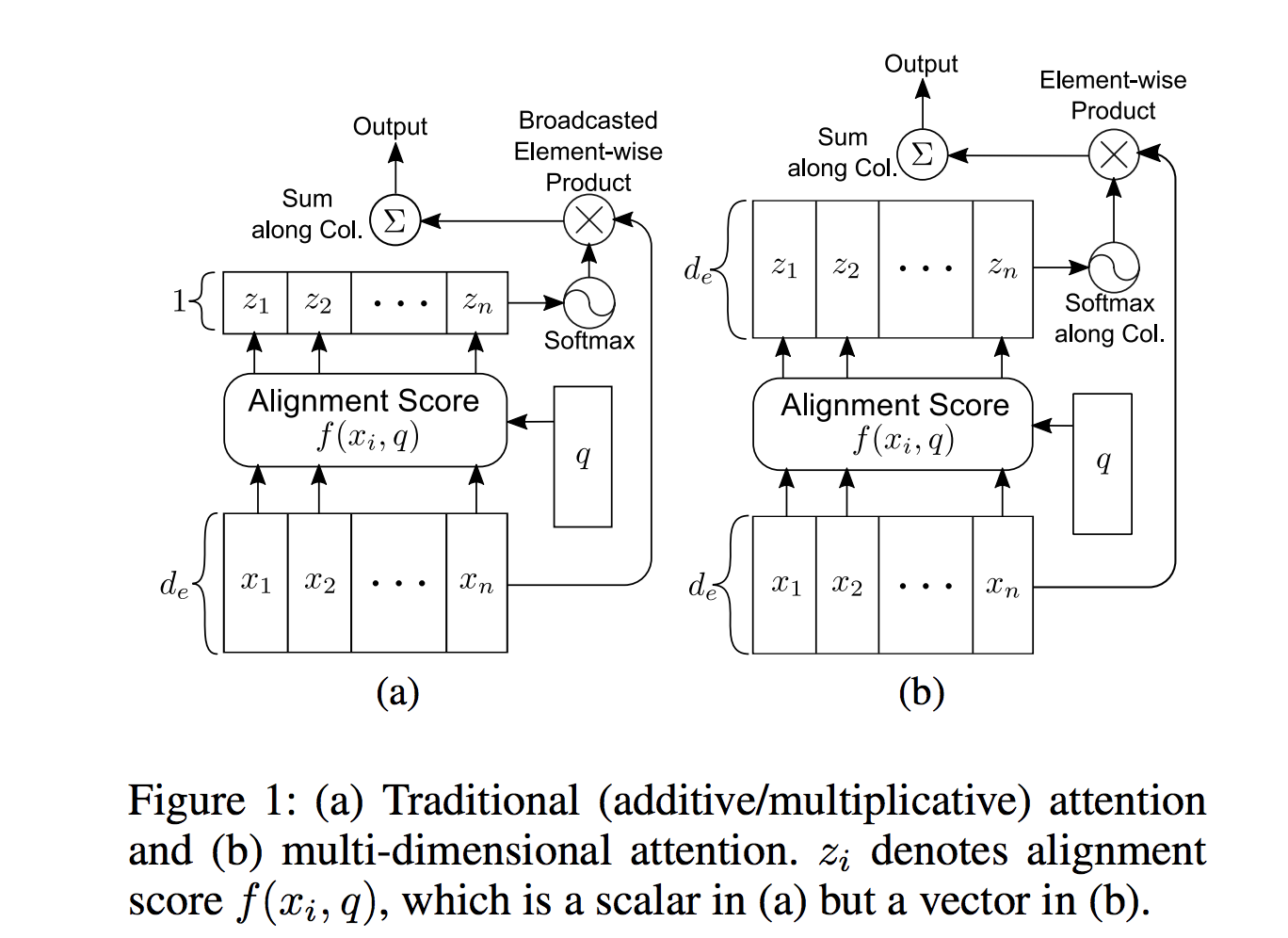
实际上主要区别在于，之前每个value向量对应一个权重Alignment Score，加权的时候实际上是利用了广播机制，value每个元素feature都乘上该权重；现在修改为在feature-level，每个元素特征都乘上不同的权重系数，因此Alignment Score是和Value同维度数的向量，即右图中的$\boldsymbol{z}_i$。做法很简单，使用MLP对齐的时候，MLP输出层神经元数量等于Value维度数即可，例如这篇文章中使用$f(x_i, q) = \boldsymbol{W}^T \sigma(\boldsymbol{W}^{(1)}\boldsymbol{x}_i + \boldsymbol{W}^{(2)} \boldsymbol{q} + \boldsymbol{b}^{(1)})+\boldsymbol{b}$

其他方式如下：($f(\boldsymbol{u}, \boldsymbol{v})$)

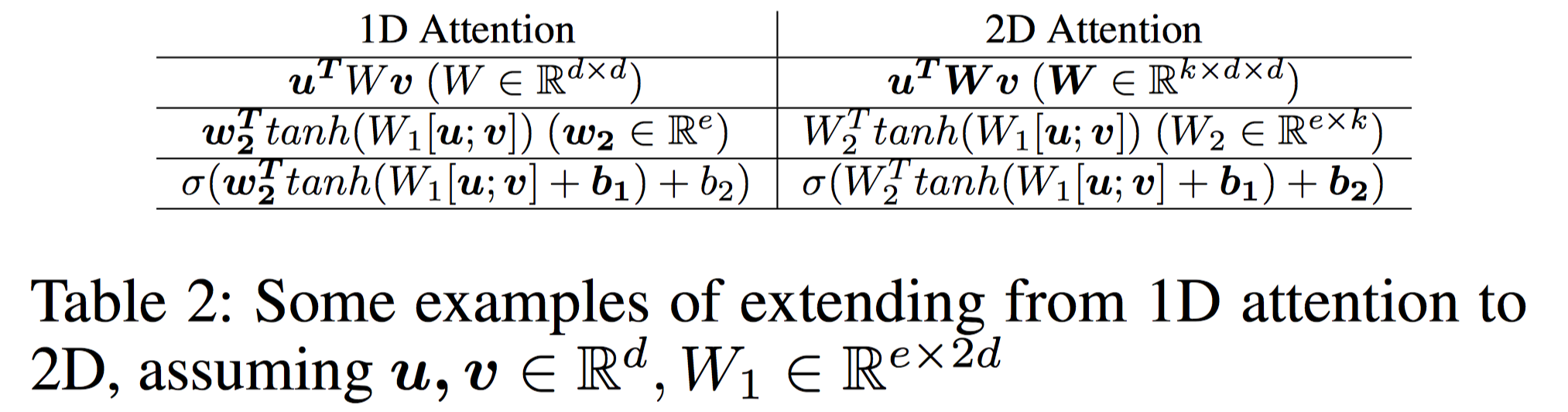
Multi-Source Attention

NAACL-HLT2016：Multi-Source Neural Translation

这是2016发表在NAACL-HLT的一篇文章。文章使用英语，德语，法语三种语言建立了一种多源（三语言）机器翻译模型。Intuition在于，如果一篇文章被翻译成了另一种语言，那么就更加倾向于被翻译成其他语言。这样的观点对机器翻译任务有一定的启发，将原本的单一源语言替换为多种源语言，应该可以取得更好的效果。如英语中的“bank”一词原本可以翻译为河岸或是银行，如果源语言中有德语词汇“Flussufer”（河岸）作为帮助，则自然可以精确得到法语中“Berge”（河岸）这样的翻译结果。基于这样的思想，作者在原有的seq2seq+attention模型的基础上做了修改，引入更多源语句，建立一种多源的翻译模型。模型结构如下：

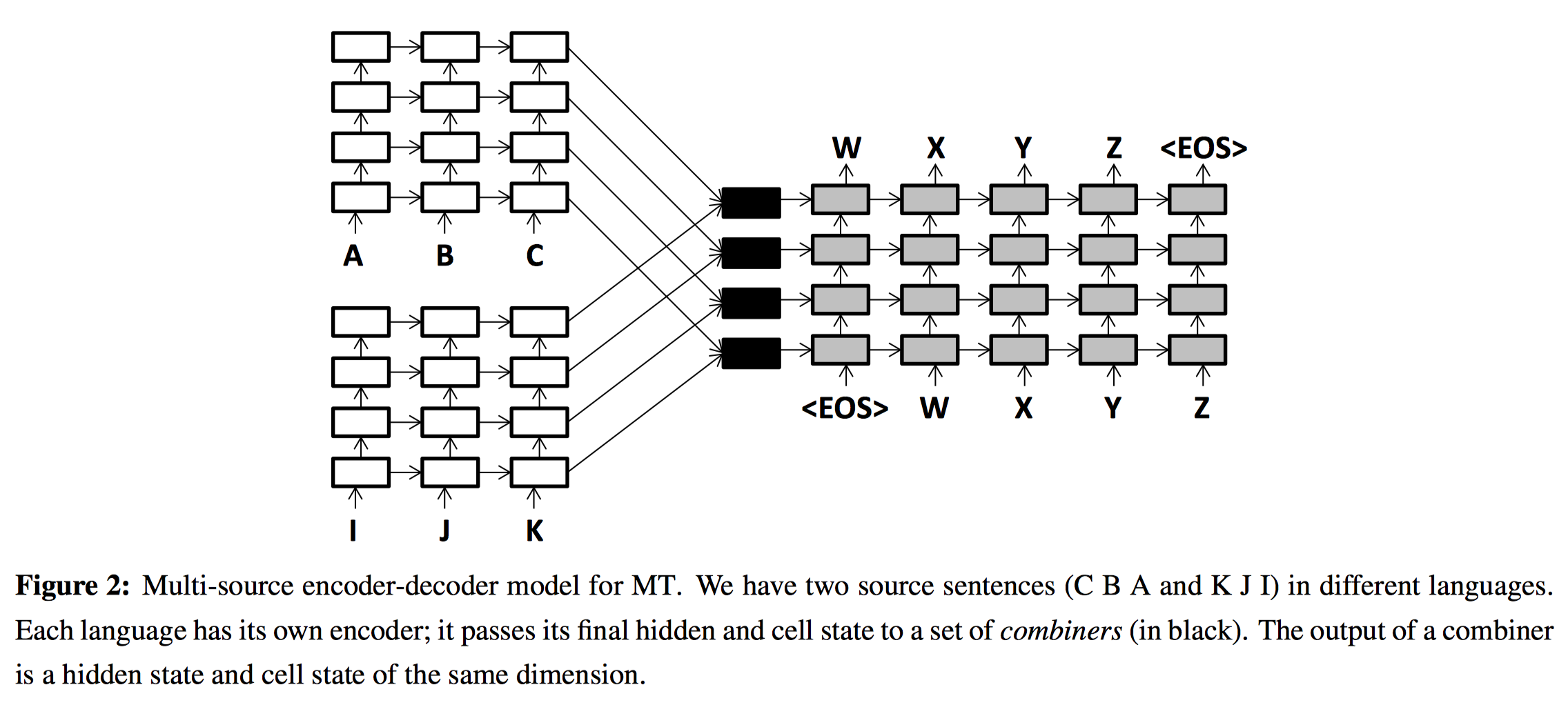
左侧是两种不同语言的源语句，每种语言的源语句都有一个自己的encoder，且结构一样。问题的关键在于如何将两种语言encoder的东西combine在一起，并和decoder的表示进行对齐求attention。由于作者采用了LSTM，因此同时考虑了hidden state和cell state的combination。核心工作就是图中黑色部分的combiners。combiners的输入是两个源语句最后时刻encoder得到的hidden state $\boldsymbol{h}_1, \boldsymbol{h}_2$和cell state $\boldsymbol{c}_1, \boldsymbol{c}_2$，输出是单个hidden state $\boldsymbol{h}$和单个cell state $\boldsymbol{c}$。（以往的工作似乎没有把encoder的cell state给decoder，从图中还可以看出，两个encoder中，每一层得到的两个源语句的hidden state和cell state都需要经过combiners）

最基本的combiner：对于hideen state，就是把两个encoder的隐状态concat起来，再做一个线性变换+tanh激活：$\boldsymbol{h} = tanh(\boldsymbol{W}_c [\boldsymbol{h}_1 ; \boldsymbol{h}_2 ])$。对于cell state，直接相加: $\boldsymbol{c}=\boldsymbol{c}_1+\boldsymbol{c}_2$。
LSTM variant combiner:
$$
\begin{aligned}
\boldsymbol{i} &= \text{sigmoid}(\boldsymbol{W}_1^{i} \boldsymbol{h}_1 + \boldsymbol{W}^{i}_2 \boldsymbol{h}_2) \\
\boldsymbol{f}_j &= \text{sigmoid}(\boldsymbol{W}_j^f \boldsymbol{h}_j), j=1,2 \\
\boldsymbol{o} &= \text{sigmoid}(\boldsymbol{W}_1^{o} \boldsymbol{h}_1 + \boldsymbol{W}^{o}_2 \boldsymbol{h}_2)\\
\boldsymbol{u} &= \text{tanh}(\boldsymbol{W}_1^{u}\boldsymbol{h}_1 + \boldsymbol{W}_2^{u}\boldsymbol{h}_2) \\
\boldsymbol{c} &= \boldsymbol{i} \odot \boldsymbol{u} + \boldsymbol{f}_1 \odot \boldsymbol{c}_1 + \boldsymbol{f}_2 \odot \boldsymbol{c}_2 \\
\boldsymbol{h} &= \boldsymbol{o} \odot \tanh(\boldsymbol{c})
\end{aligned}
$$
唯一要提的就是，$\boldsymbol{h}_1,\boldsymbol{h}_2$作为输入，每个encoder得到的cell state各自对应一个自己的遗忘门。

到目前为止，都不涉及到attention。上文得到的$\boldsymbol{c}$和$\boldsymbol{h}$只是作为decoder的初始输入（前一时刻的输入，以前的Seq2Seq模型，似乎cell state没有传给decoder）。

至于attention，作者做了很小的改动。采用的是EMNLP2015: Effective Approaches to Attention-based Neural Machine Translation中的Local Attention。在这个基础上，让decoder的隐状态同时和两个encoder得到的隐状态进行对齐，并各自计算得到一个上下文向量，$\boldsymbol{c}_t^1, \boldsymbol{c}_t^2$，注意这个c是上下文向量，跟上文所述cell state无关。最后计算Decoder的Attentional Hidden State时，使用$\boldsymbol{\tilde{h}}_t = \tanh(\boldsymbol{W}_c[\boldsymbol{h}_t,\boldsymbol{c}_t^1,\boldsymbol{c}_t^2])$。也就是之前只使用1个上下文向量，这里面使用两个上下文向量。

下面是实验的一个case:

Hierarchical Attention

NAACL-HLT2016：Hierarchical Attention Networks for Document Classification

文本分类是一项基础的NLP任务，在主题分类，情感分析，垃圾邮件检测等应用上有广泛地应用。其目标是给每篇文本分配一个类别标签。本文中模型的直觉是，不同的词和句子对文本信息的表达有不同的影响，词和句子的重要性是严重依赖于上下文的，即使是相同的词和句子，在不同的上下文中重要性也不一样。就像人在阅读一篇文本时，对文本不同的内容是有着不同的注意度的。而本文在attention机制的基础上，联想到文本是一个层次化的结构，提出用词向量来表示句子向量，再由句子向量表示文档向量，并且在词层次和句子层次分别引入attention操作的模型。

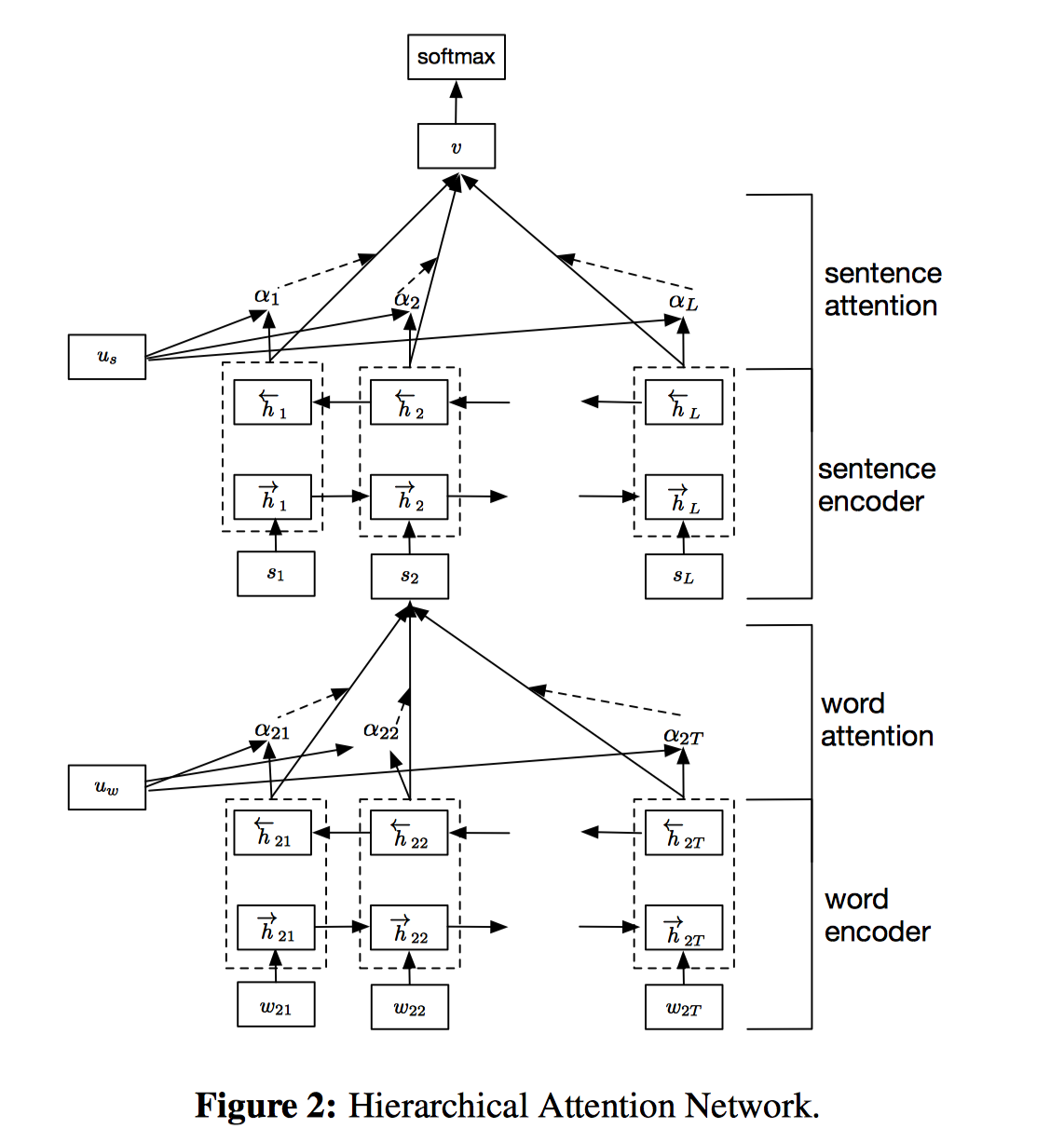
模型结构如上图所示，词先经过Bidirectional RNN(GRU)提取到word annotation，然后经过1个MLP得到word annotation对应的隐表示(这一步在Basic Attention中没有)，然后使用该隐表示和全局的word-level上下文隐向量$\boldsymbol{u}_w$进行对齐，计算相似性，得到softmax后的attention权重，最后对句子内的词的word annotation根据attention权重加权，得到每个句子的向量表示。接着，将得到的句子表示同样经过Bidirectional RNN(GRU)提取sentence annotation，再经过MLP得到对应的隐表示，接着将其和全局的sentence-level上下文隐向量$\boldsymbol{u}_s$进行对齐计算，得到句子的attention权重，最后加权sentence annotation得到文档级别的向量表示。得到文档表示后再接一个softmax全连接层用于分类。

这里最有趣的一点是，全局的word-level上下文隐向量$\boldsymbol{u}_w$和全局的的sentence-level上下文隐向量$\boldsymbol{u}_s$，是随机初始化的，且也是通过模型进行学习的。这二者就像专家一样，是高级咨询顾问。为了得到句子的向量表示，我们询问$\boldsymbol{u}_w $哪些词含有比较重要的信息？为了得到文档的向量表示，我们询问$\boldsymbol{u}_s$哪些句子含有比较重要的信息？

Attention over Attention

ACL2017：Attention-over-Attention Neural Networks for Reading Comprehension

比较巧妙，但很容易理解，直接上图：

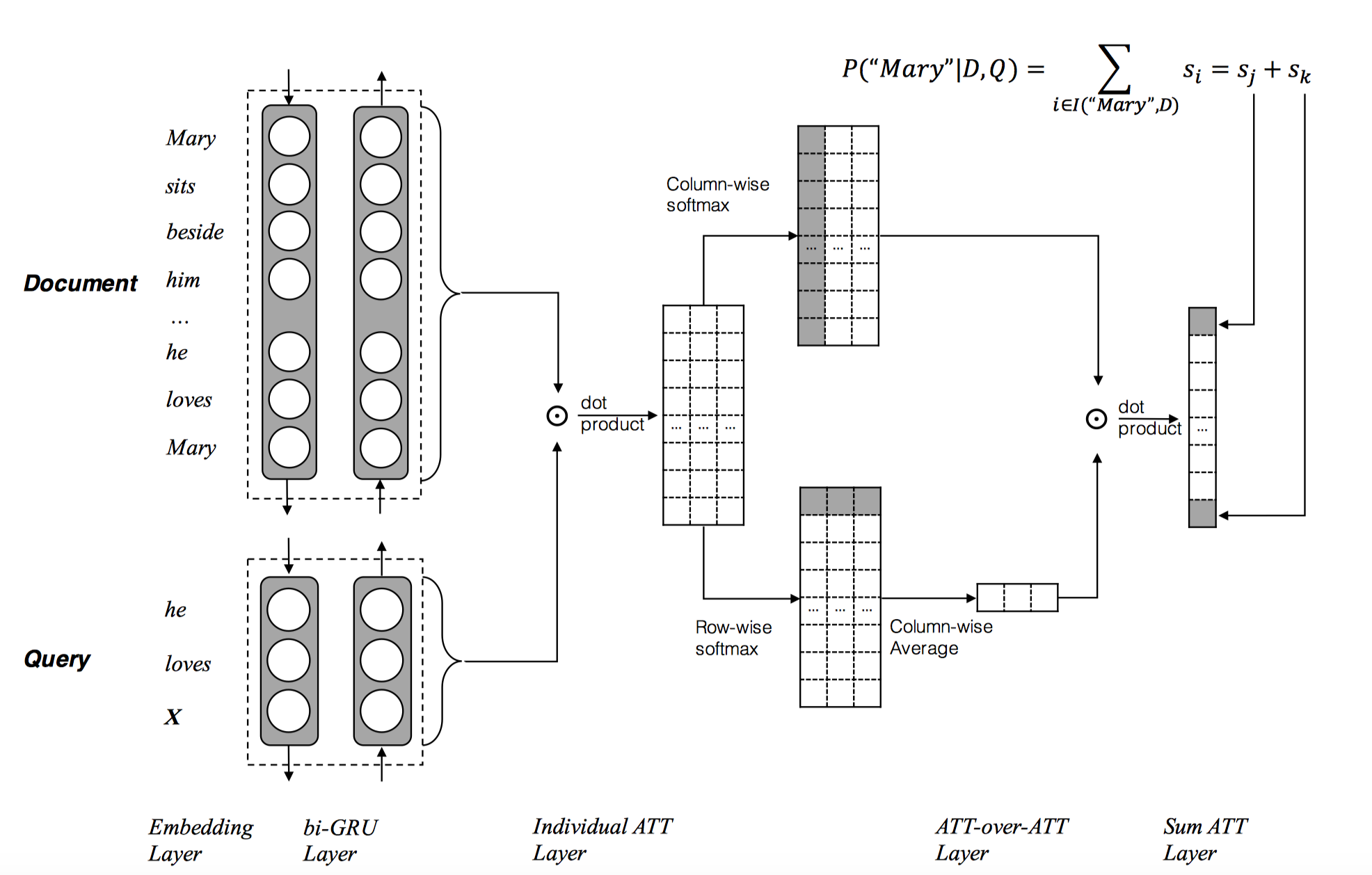
两个输入，一个Document和一个Query，分别用一个双向的RNN进行特征抽取，得到各自的隐状态$\boldsymbol{h}_{doc}$和$\boldsymbol{h}_{query}$。（Embedding Layer+Bi-GRU Layer）。接着要计算document和query之间每个词的相似性得分，

然后基于query和doc的隐状态进行dot product，得到doc和query的attention关联矩阵$M \in \mathbb{R}^{|D| \times |Q|}$（Document所有词和Query所有词和之间的关联矩阵，行是Document，列是Query）。然后按列（column）方向进行softmax操作，得到query-to-document的attention值$\alpha(t)$，表示t时刻的query word的document-level attention。按照行（row）方向进行softmax操作，得到document-to-query的attention值$\beta(t)$，表示t时刻的document word的query-level attention，再对$\beta(t)$按照列方向进行累加求平均得到averaged query-level attention值$\beta(t)$，(可以证明，按列对$\beta(t)$平均后仍然是概率分布)，这个求平均的操作可以理解为求query-level每个词和document所有词的平均关联性。

最后再基于上一步attention操作得到$\boldsymbol{\alpha}$和$\boldsymbol{\beta}$，再进行attention操作，即attention over attention得到最终的attended attention $\boldsymbol{s}=\boldsymbol{\alpha}^T \boldsymbol{\beta} \in \mathbb{R}^{|D|}$，即Document每个词都有一个attended attention score。

预测的时候，预测词典中每个词的概率，将词w在document中出现的位置上对应的attention值进行求和。例如图中Mary出现在Document首尾，故把这两个attention score相加，作为预测的概率。

文章的亮点在于，引入document和query所有词pair-wise的关联矩阵，分别计算query每个词document-level attention(传统的方法都只利用了这个attention)，和document每个词的query-level attention，对后者按列取平均得到的averaged query-level attention。进一步，二者点乘得到attended document-level attention，也即attention-over-attention。

这个和上文层次化Attention有点像。

Multi-step Attention

NIPS2017：Convolutional Sequence to Sequence Learning

2017年，FaceBook Research在论文《Convolutional Sequence to Sequence Learning》提出了完全基于CNN来构建Seq2Seq模型。Motivation在于，以往的自然语言处理领域，包括 seq2seq 任务中，大多数都是通过RNN来实现。这是因为RNN的链式结构，能够很好地应用于处理序列信息。但是，RNN也存在着劣势：一个是由于RNN运行时是将序列的信息逐个处理，不能实现并行操作，导致运行速度慢；另一个是传统的RNN并不能很好地处理句子中的结构化信息，或者说更复杂的关系信息，同时对于长语句中词依赖关系的捕捉不够好。相比之下，CNN的优势就凸显出来。最重要的一点就是，CNN能够并行处理数据，计算更加高效。此外，CNN是层级结构，与循环网络建模的链结构相比，层次结构提供了一种较短的路径来捕获词之间远程的依赖关系，因此也可以更好地捕捉更复杂的关系，具体而言低层的卷积网络可以捕获邻近的词之间的关系；高层的卷积网络以低层的卷积网络的输出作为输入，可以捕获远程的词之间的关系。另外，作者在Decoder中，使用了multi-step attention，即，在 decoder 的每一个卷积层都会进行 attention 操作，并将结果输入到下一层。有点类似于人做阅读理解时，会反复去原文中寻找是否有合适的答案（且每次寻找时，理解会加深，找的更准）。当然，这种多跳机制在下文所述的End-to-End Memory Networks中实际上已经有所体现了。

直接上模型图：(英文翻译成德文，从上到下看)

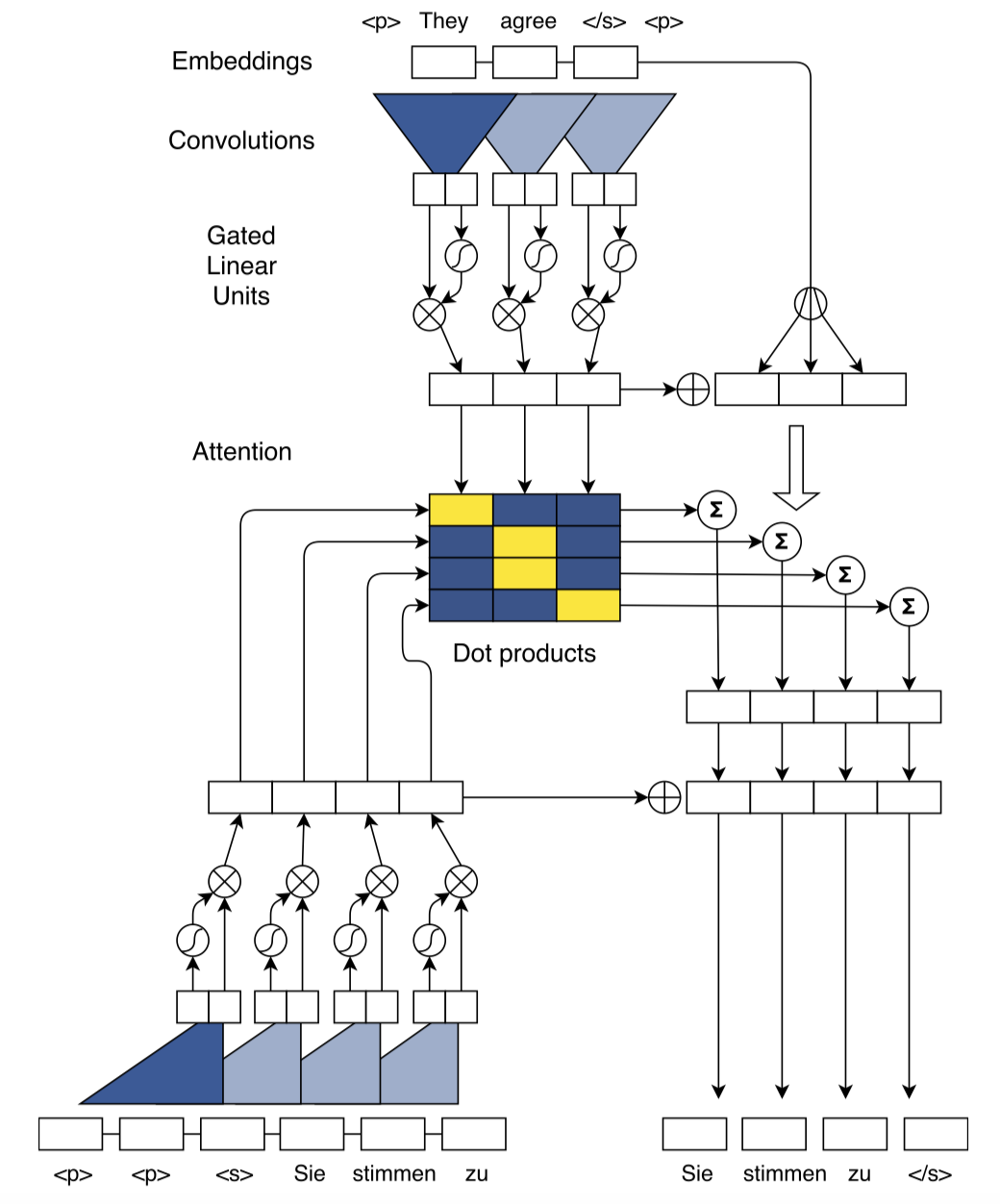
Embedding Layer：word embedding+position embedding。
Convolutional Block Structure：层级的卷积块结构，通过层级叠加能够得到远距离的两个词之间的关系信息，encoder和decoder都由多层的Convolutional Block叠加而成。每层由1个Block构成，且“卷积计算+非线性计算+残差连接”看作一个Convolutional Block。卷积计算时，以单词$i$为中心的窗口$[i-k/2, i+k/2]$内$k$个$d$维的embedding词全部concat在一起，得到输入$\boldsymbol{X} \in \mathbb{R}^{kd}$；卷积核矩阵为$\boldsymbol{W} \in \mathbb{R}^{kd \times 2d}$，可以理解为每个卷积核大小为$kd$，一共有2d个卷积核，卷积完的输出$\boldsymbol{Y}=[\boldsymbol{A}, \boldsymbol{B}] \in \mathbb{R}^{2d}$；非线性运算时，采用了门控结构（GLU），计算公式为: $v([\boldsymbol{A},\boldsymbol{B}])=\boldsymbol{A} \otimes \delta(\boldsymbol{B})$，其中$v$是非线性运算，$\delta$是门控函数。也就是说上述2d个卷积核，卷积得到的前d个元素构成的向量为A，后d个元素构成的向量为B，且B作为门控函数的输入。$v$的输出也是d维的。残差连接时(GLU的右侧），直接加上单词$i$的embedding得到一个Block的输出。作者为了保证卷积的输出长度和输入长度一致，添加了padding策略。这样多个Blocks可以叠加在一起。Decoder最后一层Block的输出经过softmax全连接层得到下一个词的概率。
Multi-step Attention：上面描述还未使用到Attention，只不过用多层卷积块分别提取了Encoder表示和Decoder表示，Decoder还未用到Encoder的信息。Multi-step意味着Decoder每一个卷积层都会进行Attention。首先将Decoder经过卷积层提取到的特征表示和前一个已经预测的输出词的embedding结合在一起，$\boldsymbol{d}_i^l = \boldsymbol{W}_d^l \boldsymbol{h}_i^l + \boldsymbol{b}_d^l + \boldsymbol{g}_i$，再和Encoder最后一个Block提取的特征表示$\boldsymbol{z}_j^u$（$u$是Encoder最后一个Block）求Attention（点乘+softmax），记做$a_{ij}^{l}$。接着计算上下文向量，除了利用$\boldsymbol{z}_j^u$，还利用了对应单词的embedding，则$\boldsymbol{c}_i^l =\sum_{j=1}^m a_{ij}^l(\boldsymbol{z}_j^u+ \boldsymbol{e}_j)$。最后将$\boldsymbol{c_i}^l$加到Decoder的特征表示上$\boldsymbol{h}_i^l$上($\boldsymbol{c_i}^l+\boldsymbol{h}_i^l$)，作为Block的输出，且是Decoder下一个Block的输入。如此，在Decoder每一个卷积层都会进行 attention 的操作，得到的结果输入到下一层卷积层，这就是多跳注意机制multi-hop attention。这样做的好处是使得模型在得到下一个注意力时，能够考虑到之前的已经注意过的词。

Attention with Pointer/Copying mechanism

NIPS2015：Pointer Networks

ACL2016：Incorporating Copying Mechanism in Sequence-to-Sequence Learning

ACL2017：Get To The Point: Summarization with Pointer-Generator Networks

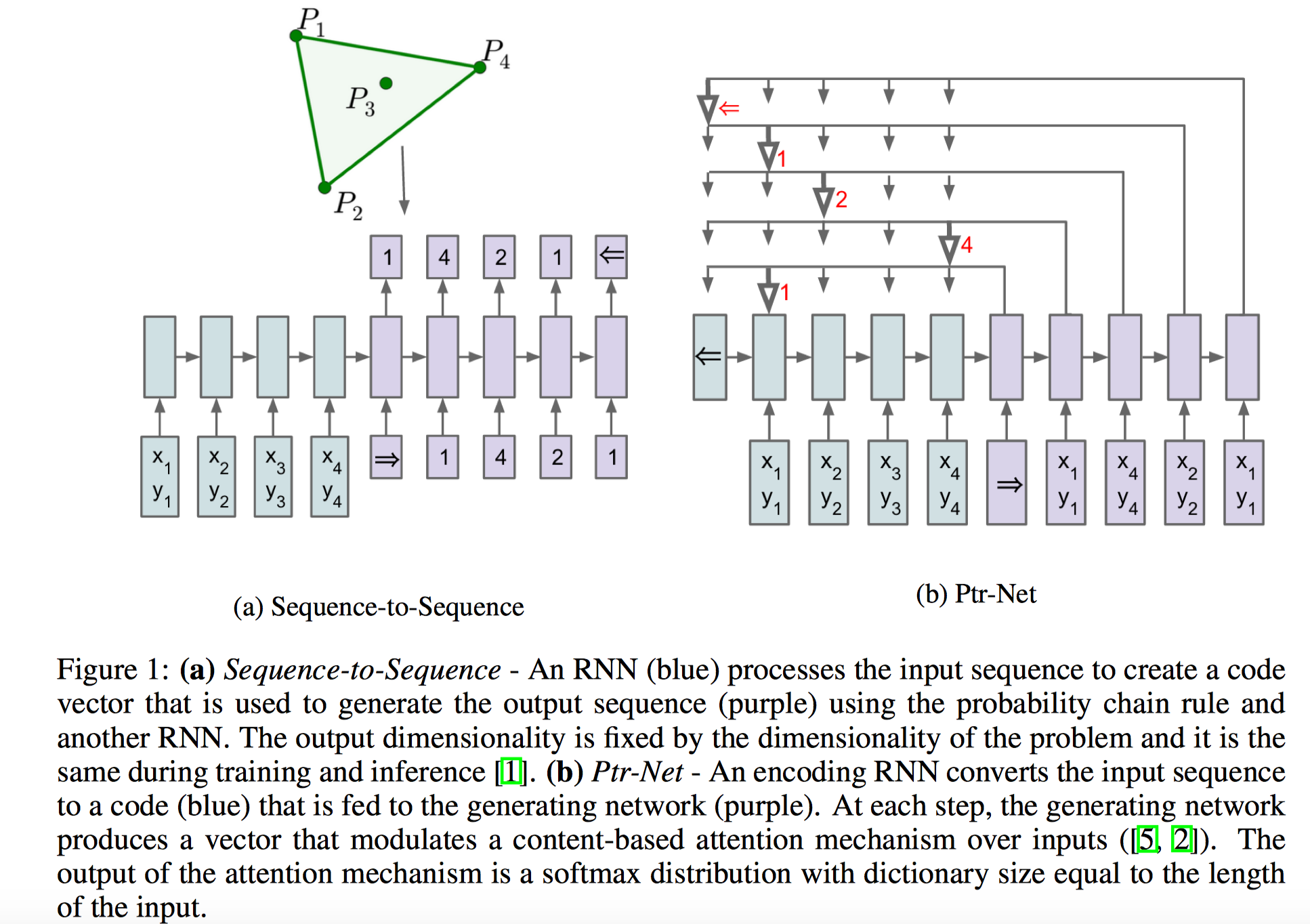
首先是“NIPS2015：Pointer Network“。作者想解决的是输出序列语句中每个元素是离散的单词，且该元素和输入序列语句中每个位置相对应的应用场景（an output sequence with elements that are discrete tokens corresponding to positions in an input sequence，说白了就是拷贝），如寻找凸包(比如训练的时候最多4个顶点，后来遇到10个顶点的几何图形就解决不了了)等。这种场景的特点是，输出序列的词汇表会随着输入序列长度的改变而改变，也就是说对很多样例而言，out-of-vocabulary现象是经常存在的。传统的seq2seq模型无法解决该问题，因为对于这类问题，输出往往是输入集合的子集，且输出的类别词汇表是可变的。基于这种特点，作者考虑能不能找到一种结构类似编程语言中的指针，每个指针对应输入序列的一个元素，从而我们可以直接操作输入序列而不需要特意设定输出词汇表。作者给出的答案是指针网络（Pointer Networks）。Pointer Networks的核心思想在于，直接将输入序列对应的Attention Score向量作为Pointer指针来选择输入序列的一部分作为输出，因为Attention可以衡量不同输入序列token的重要性程度（而先前的Attention Score用于加权encoder的隐状态并得到一个上下文向量用于Decoder阶段）。

总结一下，传统的带有注意力机制的seq2seq模型的运行过程是这样的，先使用encoder部分对输入序列进行编码，然后对编码后的向量做attention，最后使用decoder部分对attention后的向量进行解码从而得到预测结果。但是作为Pointer Networks，得到预测结果的方式便是输出一个概率分布，也即所谓的指针。换句话说，传统带有注意力机制的seq2seq模型输出的是针对输出词汇表的一个概率分布，而Pointer Networks输出的则是针对输入文本序列的概率分布。直接优化该概率分布的交叉熵损失即可。

接着我们先介绍下ACL2017应用Pointer Network的文章“Get To The Point: Summarization with Pointer-Generator Networks“，这篇文章略好懂一些。作者提出了Pointer-Generator模型，在传统的Attention Encoder-Decoder基础上加入了Pointer Network+Coverage技术来解决文本摘要的seq2seq模型存在的两大缺陷：1、模型容易不准确地再现事实细节，也就是说模型生成的摘要不准确；2、往往会重复，也就是会重复生成一些词或者句子。模型结构如下：

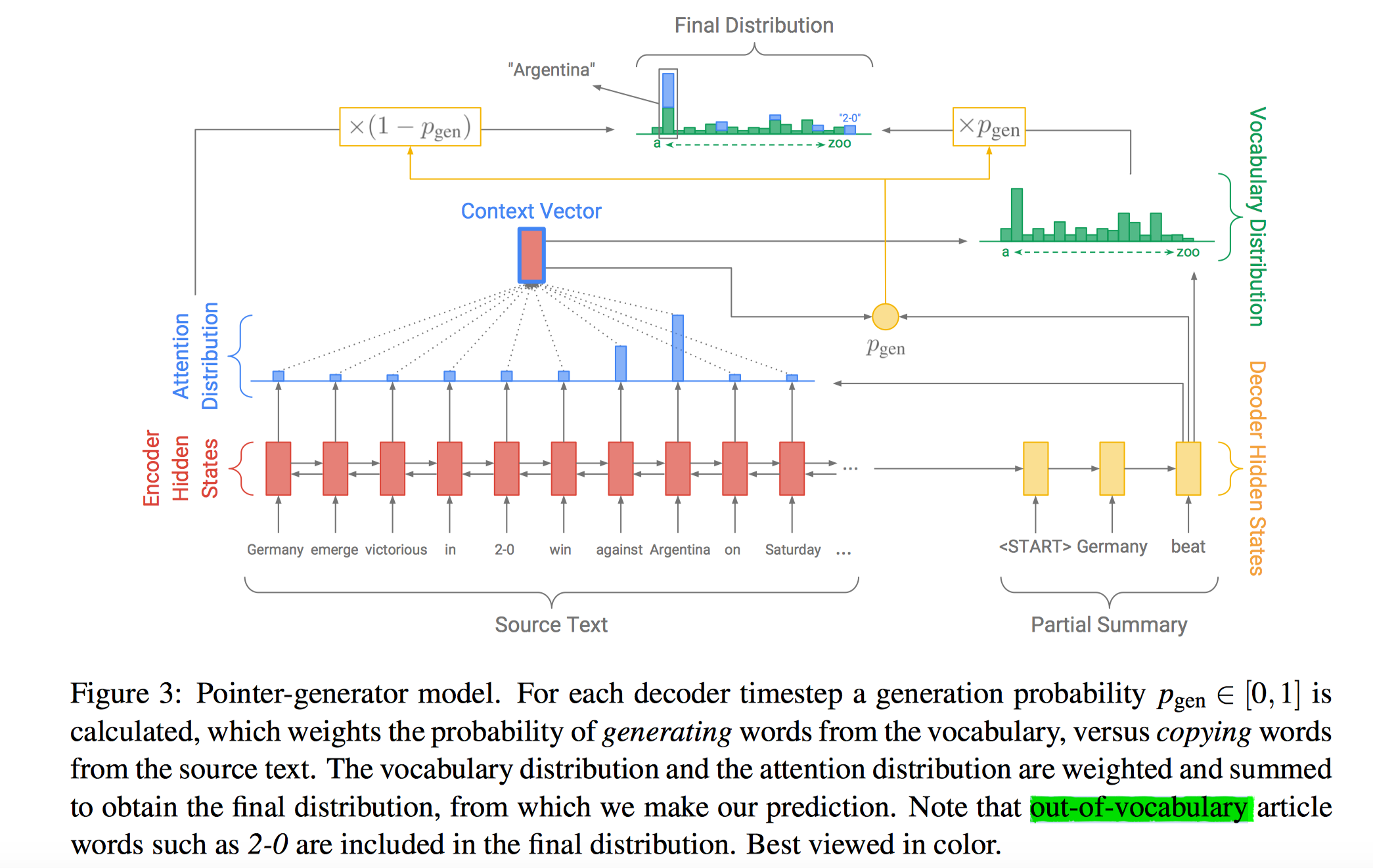
这里主要介绍Pointer Networks部分。作者对Pointer Networks应用的思想非常直观，就是用它来复制源文本中的单词。简单来说，在每一次预测的时候，通过传统seq2seq模型的预测（即softmax层的结果）可以得到针对词汇表的概率分布（图中绿色柱形图），然后通过Pointer Networks可以得到针对输入序列的概率分布（图中蓝色柱形图），对二者做并集就可以得到结合了输入文本中词汇和预测词汇表的一个概率分布（最终结果的柱形图中的“2-0”这个词不在预测词汇表中，它来自输入文本），这样一来模型就有可能直接从输入文本中复制一些词到输出结果中。当然，直接这样操作未必会有好的结果，因此作者又加入了一个$P_{gen}$来作为soft概率。Pgen的作用可以这样理解：决定当前预测是直接从源文本中复制一个词过来还是从词汇表中生成一个词出来，二者通过插值combine起来。
$$
p(w)=p_{gen}P_{\text{vocab}}(w)+(1-p_{gen})\sum_{i:w_i=w} a_{i}^t
$$
其中，$p_{gen}$根据上下文向量，decoder层隐状态，decoder输入，经过1层MLP+sigmoid得到。$P_{\text{vocab}}(w)$是Decoder输出层得到的词汇表中$w$的概率，$\sum_{i:w_i=w} a_{i}^t$则是对输入序列中，$w$词对应的attention值加起来(可能多次出现)。

最后是ACL2016的文章“Incorporating Copying Mechanism in Sequence-to-Sequence Learning”，几乎和ACL2017文章思想一样。文章创新点包括3个部分：

预测：基于两种模式的混合概率模型预测下一个词的概率分布。包括：Generation-Mode，用来根据词汇表生成词汇，计算词汇表词的生成概率；Copy-Mode，用来直接复制输入序列中的一些词，计算源语句序列词被拷贝的概率。最后预测时，二者概率相加（上一篇文章根据$p_{gen}$插值，这里直接相加）。因此，该模型具备解决OOV问题的能力。
Decoder隐状态的更新：传统的Seq2Seq模型在Decoder层计算下一个时刻的隐状态时，使用的信息包括前一时刻隐状态，attention后的上下文状态，前一时刻已经预测的输出词的embedding。而该模型中，还使用了前一时刻已经预测的输出词在源语句Encoder中对应的特定位置的隐状态（因为前一时刻的输出词可能是来自于源语句序列的拷贝，故在Encoder中有对应的隐状态）。
Encoder隐状态的使用方式：传统的Seq2Seq模型对于Encoder隐状态的使用只包括Attention Read，即转成attentional上下文向量在Decoder中使用，这可以看做是Content-based Addressing。而本文还加了一种使用方式Selective Read，也就是上述”Decoder隐状态更新”中所述，会使用前一时刻已经预测的输出词在源语句Encoder中对应的特定位置的隐状态，这种方式可以看做Location-based Addressing（伴随着信息的流动，下一个位置的信息在预测下一个Decoder隐状态时会被关注，因此Location-based Addressing使得模型具备拷贝源语句某个连续子序列的能力）。

模型结构如下：

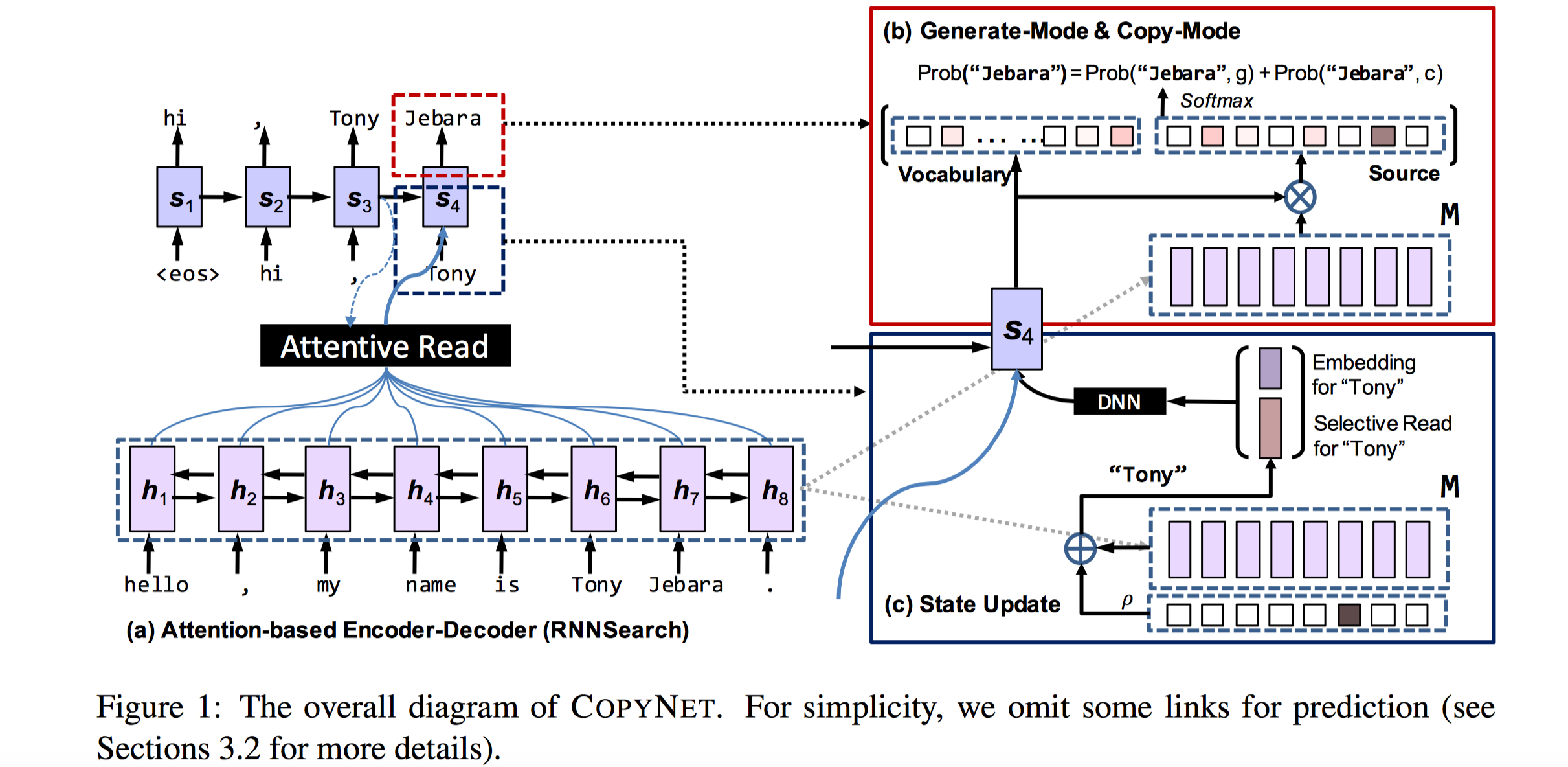
上图解读分成3部分，首先令Encoder得到的所有hidden state为矩阵$\boldsymbol{M}$。目前要预测当前时刻的输出词 Jebara。

左侧和常规的Attention模型一致，在预测此刻输出词”Jebara”时，使用前一时刻的Decoder隐状态$\boldsymbol{s}_3$和$\boldsymbol{M}$求Attention，该Attention得分向量作为源语句每个词的概率分布（文中好像用的是$\boldsymbol{s}_4$，那这个应该是未更新前的）。
右侧下半部分，根据$\boldsymbol{s}_{t-1}$，$\boldsymbol{y}_{t-1}$， $\boldsymbol{c}$，$\boldsymbol{M}$更新此刻的Decoder状态$\boldsymbol{s}_t$。重点是前一时刻输出词$\boldsymbol{y}_{t-1}$(Tony)除了它的embedding之外，作者还考虑了如果前一时刻的输出词是输入序列某个位置的词，例如Tony就是输入序列的词，那么利用Attention向量对这些输入词的Encoder hidden state进行加权作为对输入序列的Selective Read（此处是Tony，但是Tony可能出现多次；如果没有出现，那么这部分为空，退化为传统的方法）。然后将Tony的Embedding和Selective Read连接在一起作为$\boldsymbol{y}_{t-1}$。最后一起经过LSTM/GRU得到此刻的$\boldsymbol{s_t}$。
最后右侧上半部分，Decoder根据生成模式和拷贝模式计算下一个词的概率分布。词语分成3大部分，源序列输入词，词汇表词，未知词(统一设置成UNK)。下一个词概率分布：
$$
p(\boldsymbol{y}_t |\boldsymbol{s}_t , \boldsymbol{y}_{t−1}, \boldsymbol{c}_t, \boldsymbol{M}) = p(\boldsymbol{y}_t , \text{g} |\boldsymbol{s}_t , \boldsymbol{y}_{t−1}, \boldsymbol{c}_t ,\boldsymbol{M}) + p(\boldsymbol{y}_t ,\text{c}|\boldsymbol{s}_t , \boldsymbol{y}_{t−1}, \boldsymbol{c}_t, \boldsymbol{M})
$$
其中，第一个式子是生成模式（g），对应右上图左侧；第二个词时拷贝模式（c），对应右上图右侧。具体不同模式词汇的概率分布都是先根据得分模型(MLP)计算不同词的得分，再进行softmax得到分布；生成模式得分模型依赖于上一步计算的$\boldsymbol{s}_t$和输出词的embedding表示；拷贝模式得分模型依赖于$\boldsymbol{s}_t$和输入词的hidden state(M中某列)。$p(\boldsymbol{y}_t|\cdot)$所有计算情况如下图所示，图中$\varphi$就是得分模型。

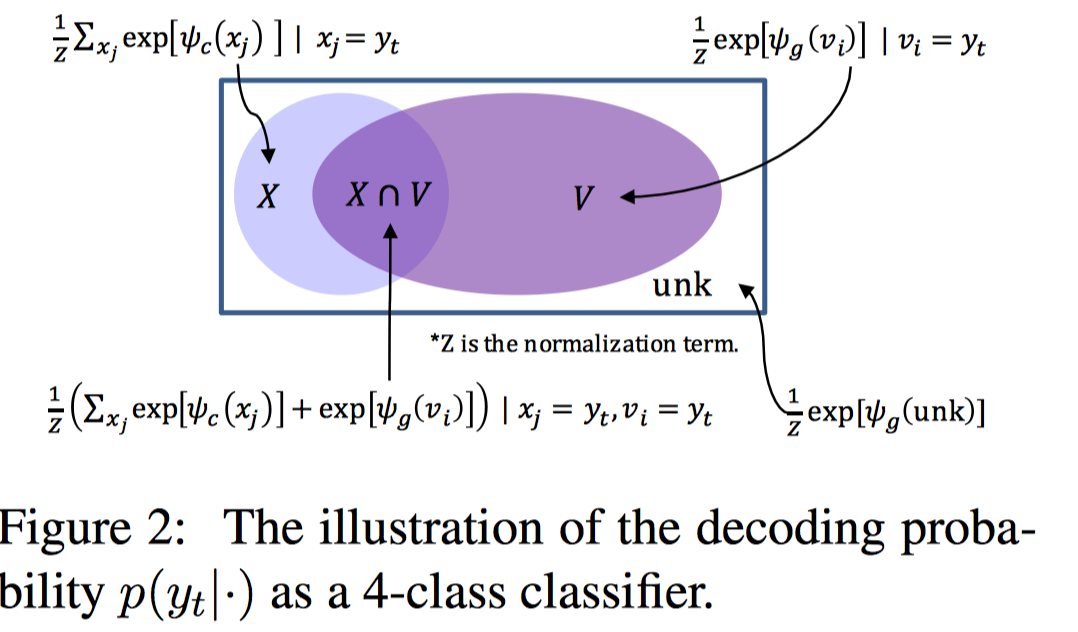
图中，$X$是源序列输入词；$V$是词汇表的词；unk是未知词。某个输出词可能属于上述4种情况中的一种。

Memory-based Attention

ICLR 2015：Memory Networks

NIPS2015：End-To-End Memory Networks

ACL2016：Key-Value Memory Networks for Directly Reading Documents

ICML2016：Ask Me Anything:Dynamic Memory Networks for Natural Language Processing

基于记忆的Attention机制将注意力分数的计算过程重新解释为根据查询/问题$q$进行soft memory addressing的过程，将编码视为从基于attention分值的memory中查询注意力分支的过程。从重用性的角度上，这种注意力机制能够通过迭代memory更新(也称为多跳)来模拟时间推理过程，逐步将注意力引导到正确的答案位置，对于答案和问题没有直接关系的复杂问答效果较好（需要多步推理）。从灵活性角度看，可以人工设计key的嵌入以更好的匹配问题，人工设计value的嵌入来更好的匹配答案。这种解耦的模块化设计，能够在不同组件中注入领域知识，使模块之间的通信更有效，并将模型推广到传统问答之外的更广泛的任务。

形式化来说，memory中存储的是key-value pairs，$\{(\boldsymbol{k}_i, \boldsymbol{v}_i)\}$，给定一个查询$\boldsymbol{q}$。定义上下文向量获取3步骤：

$e_i = a(\boldsymbol{q}, \boldsymbol{k}_i)$ (address memory)
$\alpha_i =\frac{exp(e_i)}{\sum_j exp(e_j)}$ (normalize)
$\boldsymbol{c} = \sum_i \alpha_i \boldsymbol{v}_i$ (read contents)

实际上memory存储的就是输入序列（更准确的说是外部记忆，输入序列是一种外部记忆，也可以引入其他领域先验知识，如知识库来构造外部记忆库），只不过可以设计key和value；如果key和value相等，那么上述就退化成了Basic Attention的操作了。

首先是ICLR2015文章”Memory Network”。该模型的出发点在于，传统的深度学习模型（RNN、LSTM、GRU等）使用hidden states或者Attention机制作为他们的记忆功能（实际上是短期的内部记忆），但是这种方法产生的记忆太小了，无法精确记录一段话中所表达的全部内容，也就是在将输入编码成dense vectors的时候丢失了很多信息。所以本文就提出了一种可读写的外部记忆模块（external memory），并将其和inference组件联合训练，最终得到一个可以被灵活操作的记忆模块。

这篇文章的贡献在于提出了一种普适性的模型架构memory networks。其核心组件包括4部分：

简单来说，就是输入的文本经过Input模块编码成向量，然后将其作为Generalization模块的输入，该模块根据输入的向量对memory进行读写操作，即对记忆进行更新(最基本的更新就是将memory划分为slots，以slot为单位进行读写，更新的时候，最简单的方法就是$\boldsymbol{m}_{H(x)}= I(x)$，即新根据输入x进行Hash索引，然后替换掉某个Slot为最新的input的内部特征表示)。然后Output模块会根据Question（也会进过Input模块进行编码）对memory的内容进行权重处理(Question会触发对memory的Attention)，将记忆按照与Question的相关程度进行组合得到输出向量，最终Response模块根据输出向量编码生成一个自然语言的答案出来。

接着是NIPS2015的文章“End-To-End Memory Networks”。作者的应用场景是问答系统（比较复杂的问答推理），包括3要素，input-question-answer。

首先介绍下语句表示组件（对应上篇论文的I组件）。语句表示组件的作用是将语句表示成一个向量。作者在bag-of-words(BoW)基础上添加位置序列信息。令某个语句为为$\boldsymbol{x}_{i} = \{\boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in}\}$。则语句向量化表示为：
$$
\boldsymbol{m}_i = \sum_j \boldsymbol{l}_j \cdot \boldsymbol{A} \boldsymbol{x}_{ij}
$$
其中，$\boldsymbol{A} \boldsymbol{x}_{ij}$看做是每个单词的embedding表示，$l_j$是根据位置计算的权重向量，称作position encoding。
$$
l_{kj} = (1 − j/J) − (k/d)(1 − 2j/J)
$$
$J$是语句长度，$j$是单词序号，$k$代表$\boldsymbol{l}_j$的第$k$个元素，$d$是Embedding的维度数($\boldsymbol{A} \boldsymbol{x}_{ij}$维度数)。

此外，语句之间也存在时序关系，作者对语句之间的时序也进行了encoding，但是一笔带过。坐在在计算$\boldsymbol{m}_i$ 和 $\boldsymbol{c}_i$ 时加了一个额外的叫做 temporal encoding的模型，$m_{i}=\sum_{j} \boldsymbol{A} \boldsymbol{x}_{ij} + T_{\boldsymbol{A}}(i)$。$T_{A}$是个矩阵，编码了时序信息，也是需要学习。当然，Position encoding和Temporal Encoding可以同时考虑。

下面要介绍的模型的memory input/output, question都需要利用该组件进行向量化表示，只不过Embedding矩阵不同。

首先给出模型架构图：

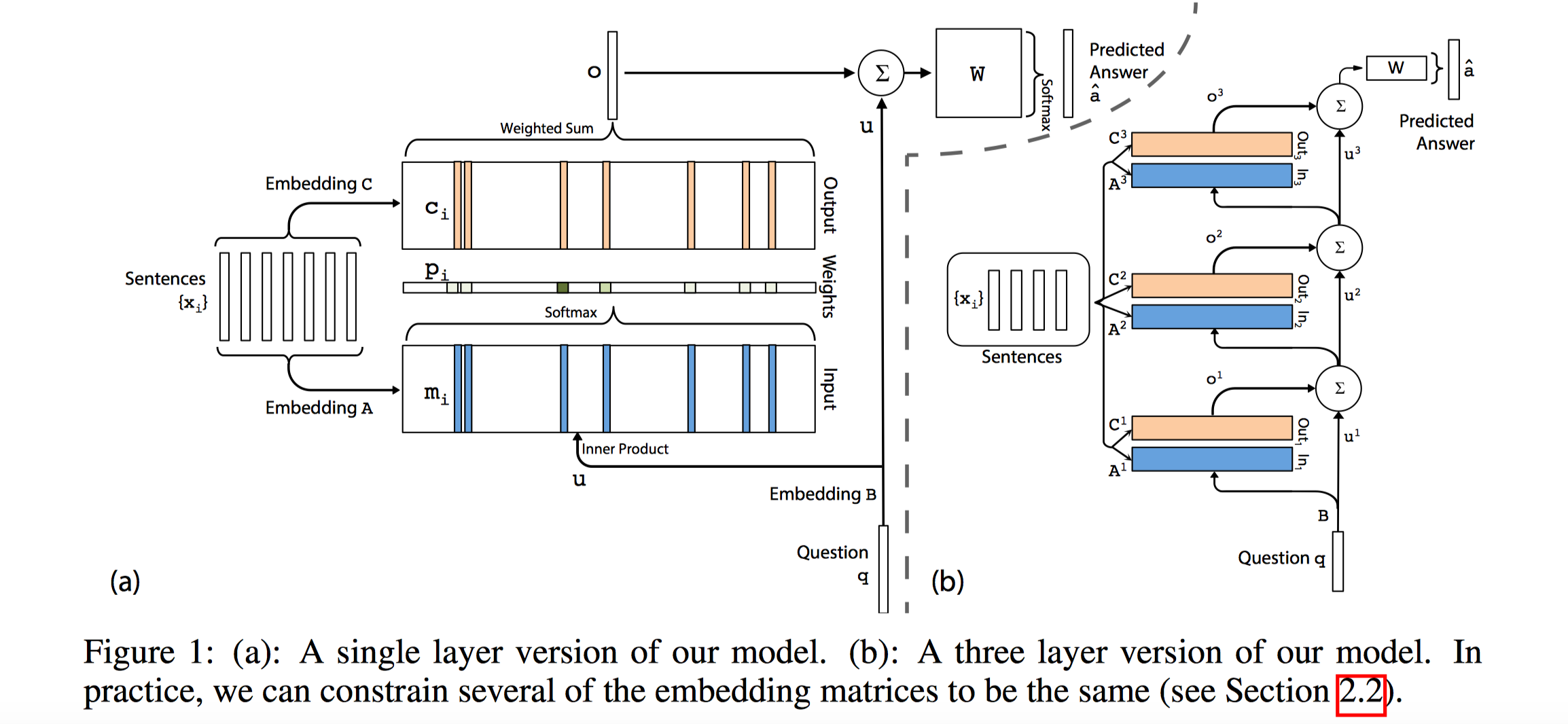
上图左侧(a)是单层的网络结构。最左边的就是memory，里面存储着输入集合$\{\boldsymbol{x}_i\}$，每个$\boldsymbol{x}_i=\{\boldsymbol{x}_{i1}, \boldsymbol{x}_{i2},…, \boldsymbol{x}_{in}\}$代表一个句子。memory的输入和输出不同，按照我的理解memory的输入是key，输出是value。输入key用于计算和查询的相似性，输出value用于计算上下文向量。

对于输入记忆(可以理解为Key memory，记忆的一种表现形式)，即图中下半部分蓝色线条，使用上述语句表示组件（Embedding A）将每个语句$\boldsymbol{x}_i$转成向量表示$\boldsymbol{m}_i$作为memory的输入（可以理解为$\boldsymbol{m}_i$存储在memory中，不断写入memory直到fixed buffer size），即key，memory input用于得到memory不同语句的attention得分向量。首先将问题语句$\boldsymbol{q}$也使用语句表示组件（Embedding B）转成向量化表示$\boldsymbol{u}$，即query，然后根据key和query和计算$p_i= Softmax(\boldsymbol{u}^T \boldsymbol{m}_i )$，这是address memory+normalize操作。

对于输出记忆(可以理解为Value memory，记忆的另一种表现形式)，即图中上半部分黄色线条，首先根据语句表示组件(Embedding C)将语句转成$\boldsymbol{c}_i$作为memory的输出，即value，然后利用该输出以及$p_i$，加权得到attentional上下文向量，即：$\boldsymbol{o} = \sum_i p_i \boldsymbol{c}_i$，这是read contents操作。

最后预测的时候，将问题表示$\boldsymbol{u}$和上下文向量$\boldsymbol{o}$相加，经过Softmax全连接层预测答案的概率分布（文中似乎只针对单个单词的答案。对于多个单词的答案，会把答案句子看成一个整体，从多个候选的答案句子中选择其中一个），$\hat{\boldsymbol{a}} = Softmax(\boldsymbol{W}(\boldsymbol{o} + \boldsymbol{u}))$，其中，$\boldsymbol{W} \in \mathbb{R}^{V \times d}$。$\hat{\boldsymbol{a}}$是词汇表所有词的概率，使用交叉熵损失进行训练。

上述是单层网络，作者将多个单层网络stack在一块，来解决多跳(Multi-Hop)操作(我的理解是每一跳都要和memory交互，形成更有用的记忆上下文向量$\boldsymbol{o}$，并不断更新查询语句表示$\boldsymbol{u}$，将注意力引导向正确的答案（查询表示向量基础上加上记忆上下文向量进行Transition，来引导到最佳答案位置），如上图(b)所示。从图中可以看出，每经过一层都要和memory交互，且后一层的问题语句表示为，$\boldsymbol{u}^{k+1}= \boldsymbol{u}^k + \boldsymbol{o}^k$。为了减少参数量，作者对$\boldsymbol{A}$，$\boldsymbol{C}$，$\boldsymbol{W}$矩阵做了限制，比如后一层的$\boldsymbol{A}$为前一层的$\boldsymbol{C}$；最后的$\boldsymbol{W}$是最后一层的$\boldsymbol{C}^{k}$。

对于这里面memory的理解，我个人认为memory会使用所有的问答系统的输入语句经过语句表示模块后提取的特征表示来初始化。后面训练的时候，如果遇到的输入语句已经在memory中了，那么就直接替换其旧值来更新memory(embedding A矩阵训练过程中在更新，因此$\boldsymbol{m_i}$也会相应的更新，同理memoy的输出$\boldsymbol{c}_i$也可以更新)。如果memory的容量有限，那么先随机初始化满，后面训练的时候遇到不在memory的语句，再根据一定策略替换掉某个值（例如使用Hash策略或FIFO策略，文章没细说）。

接着是ACL2016文章，”Key-Value Memory Networks for Directly Reading Documents”。这篇文章在key和value上进一步解耦，并引入先验知识分别来设计key embedding和value embedding，也就是人工设计key的嵌入以更好的匹配问题，人工设计value的嵌入来更好的匹配答案。模型结构如下：

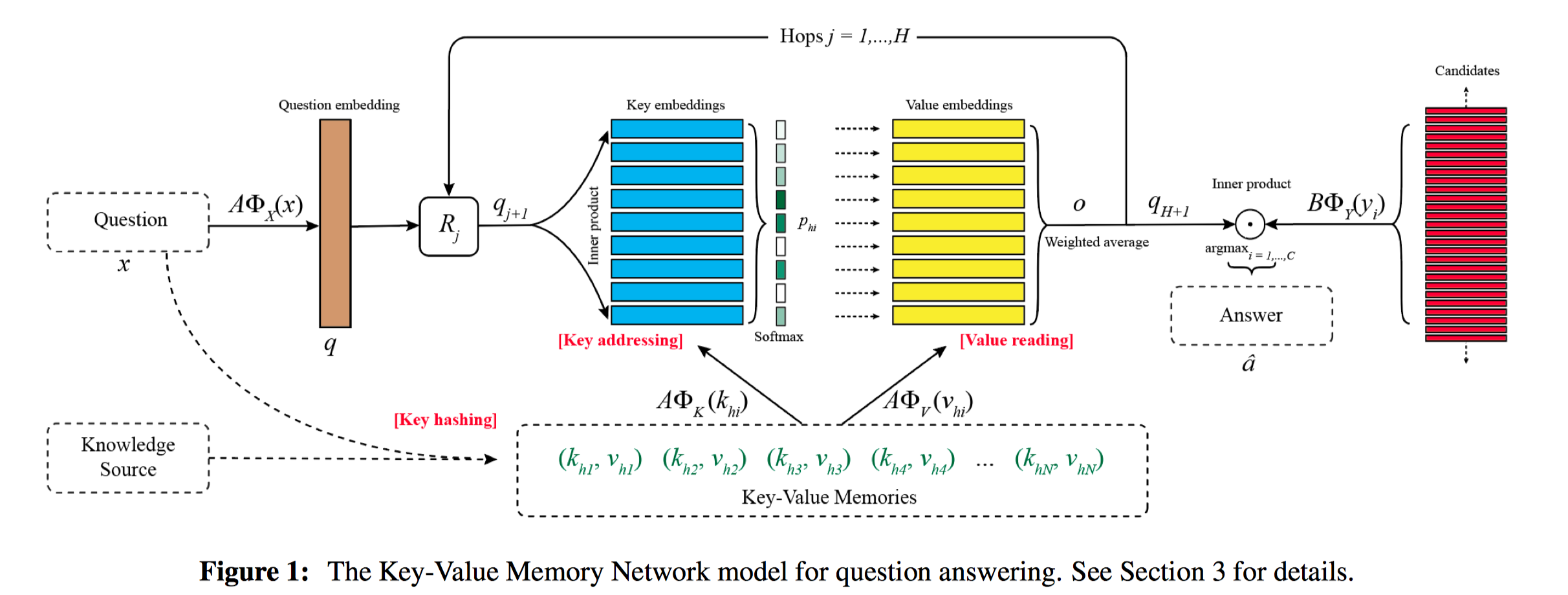
几乎一样，这里的Key Addressing就是Input Memory Addressing，Value Reading就是Output Memory Reading。核心的创新之处在于，

可以使用不同方式来映射不同的语句。Key， Value，Question，Answer，对应图中不同的$\Phi$。最简单的映射方式就是Bag-of-words，作者对Question，Answer的处理就是用BoW。而对Key和Value的处理不同。
- 使用Knowledge base引入先验，来构建记忆；作者使用知识库的结构化三元组，subject relation object，即主谓宾。然后可以使用主语和谓语作为Key，宾语作为Value。作者把三元组写成被动语句，这样一条三元组有2种形式的(key, value)。举个例子：Blade Runner directed_by Ridley Scott / Ridley Scott !directed_by Blade Runner，对于前者Key是Blade Runner directed_by，Value是Ridley Scott；对于后者Key是Ridley Scott !directed_by，Value是Blade Runner。
- Window-Level: 将文档切分成若干个windows，作者只保留中心位置是名词的windows，每个window由若干个词语构成。可以将整个window当做key来匹配问题，把中心位置名词当做value来匹配。

还有一个有趣的地方，之前的模型会限制记忆的大小，主要是因为不能保留所有的语句。这里为了解决大型记忆库的计算效率，提出了Key Hashing的概念。对于每个Question，Key Addressing过程中作者引入了Key Hashing，即可以从大型的记忆库中使用Hash索引检索出部分记忆，例如对应key里头至少有1个单词和Question相同的记忆，再根据部分记忆Address+Read。

最后是ICML2016的文章，“Ask Me Anything:Dynamic Memory Networks for Natural Language Processing“，采取了更复杂的动态记忆网络。前面两篇文章，都是使用Bag-of-Words提取语句向量化表示，这篇文章使用RNN来提取语句向量化表示。并且前面文章预测的答案一般只有1个单词，这里可以多个单词。

模型细分为Input Module，Question Module， Episodic Memory Module和Answer Module。模型结构如下：

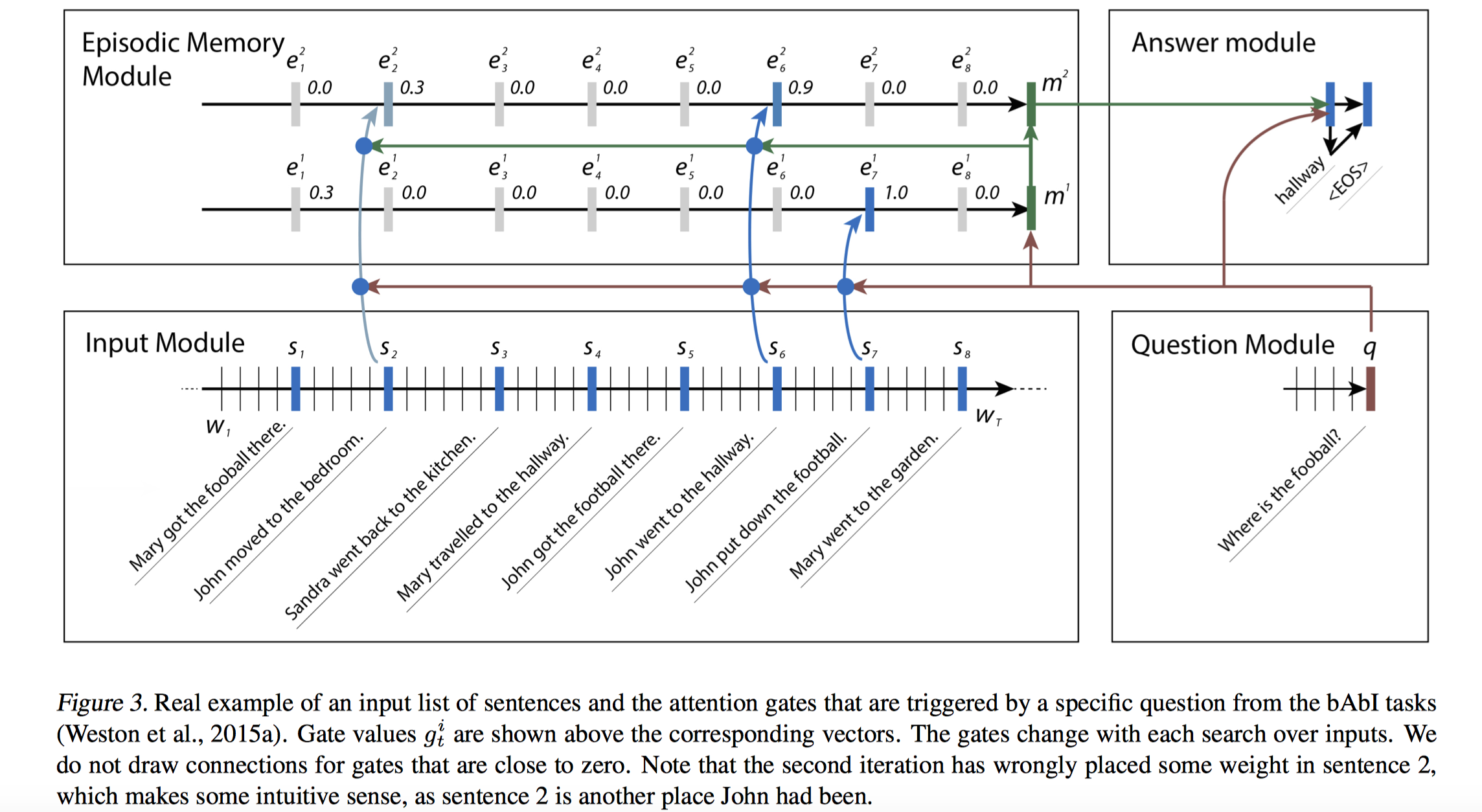
Input Module：对输入（语句，故事，文章，Wiki百科）使用GRU提取隐状态表示$\boldsymbol{c}_t$。如果输入是一句话，那么提取到的隐状态个数等于单词个数（每个单词对应一个）；如果输入是多个语句，那么提取的隐状态等于语句数（每个语句对应一个，训练时将所有语句concat在一起，语句之间添加特殊分割token，经过GRU后，保留每个token处提取到的隐状态表示，如图$\boldsymbol{c}_t=\boldsymbol{s}_t$, $t=1,2…,8$）。
Question Module：对问题使用GRU提取隐状态，不同的是只保留问题最后一个时刻得到的隐状态$\boldsymbol{q}$。
Episodic Memory Module：本模块和Input Module是对齐的，对齐的目的是要计算Input不同Token的Attention Score值。该模块主要包含Attention机制、Memory更新机制两部分组成，每次迭代都会通过Attention机制对输入向量进行权重计算，然后生成新的记忆。第$i$次迭代过程中，
- 计算Attention Score。attention mechanism使用一个门控函数作为Attention。为了计算输入序列某个时刻的attention score，门控函数的输入是该时刻的输入序列提取的表示$\boldsymbol{c}_t$，前一次迭代的记忆$\boldsymbol{m}^{i-1}$和问题$\boldsymbol{q}$，门控函数最终输出输入序列每个token(这里是每个句子)和该问题的相似性Attention score值$g_t^i$，所有时刻的score构成Attention向量，记做$\boldsymbol{g}^{i}$。
- 更新记忆（先计算新场景Episode，再计算新记忆Memory）：
$$
\boldsymbol{h}_t^i={g}_t^i \text{GRU}(\boldsymbol{c}_t , \boldsymbol{h}_{t−1}^i) + (1 − {g}_t^i)\boldsymbol{h}_{t−1}^i \\
\boldsymbol{e}^i = \boldsymbol{h}^i_{T_c} \\
\boldsymbol{m}^i = \text{GRU}(\boldsymbol{e}^i , \boldsymbol{m}^{i−1} )
$$

Episodic Memory Module场景向量$\boldsymbol{e}^{i}$用于压缩和抽象输入序列，相当于将输入序列状态集合压缩并抽象成一个场景描述向量$\boldsymbol{e}^{i}$，这个场景描述向量是和具体问题以及具体输入都是相关的。为了计算场景向量，该模块维护了自己的隐状态$\boldsymbol{h}_t^i$，根据融合了Attention机制的第一个公式来计算；第二个公式表明，最后一个时刻得到的隐状态作为提取到的新场景$\boldsymbol{e}^i$；第三个公式再根据提取到的新场景和前一次迭代得到的记忆更新记忆。

上述过程，一般会经过多次迭代（可以理解为多跳），将最后一次迭代得到的强化的记忆作为下一个Answer Module的输入。
Answer Module：采用GRU。将上述提取到的最后一次迭代的记忆$\boldsymbol{a}_0=\boldsymbol{m}^{T_M}$作为初始隐状态，问题$\boldsymbol{q}$和前一时刻预测的输出$\boldsymbol{y}_{t-1}$作为输入，得到当前时刻的隐状态$\boldsymbol{a_t}$，接一个softmax全连接层得到该时刻输出词的概率分布。
$$
\boldsymbol{y_t} = softmax(W^{(a)} \boldsymbol{a}_t) \\
\boldsymbol{a}_t = \text{GRU}(([\boldsymbol{y}_{t−1}, \boldsymbol{q}], \boldsymbol{a}_{t−1})
$$

这篇文章的动态性我个人理解为，每输入一句话，记忆就会产生和更新，且这种记忆是Input-Level的，有点像短期的记忆（和Attention比较像，Attention也是Input-Level的短期内部记忆）。而之前3篇文章的工作，记忆库是初始的一次性读取所有输入并产生memory库，这个记忆库是Task-Level的，跟这个任务相关的数据都能用于构造该记忆库，只不过受限于容量，记忆库也需要辞旧迎新。不管如何，二者的记忆表示都需要在训练过程中不断更新。

另外，这篇文章的优点就是将Memory机制更好的应用到了Seq2Seq模型。前面的3篇工作都不是标准的Seq2Seq模型，都只是利用简单的Bag-of-Words来处理序列，预测的时候，答案要么是单个单词；要么是看成一个整体的句子。而本文则用GRU在Answer Module建模答案序列。

Self Attention

NIPS2017: Attention Is All You Need

Google Brain团队在2017年提出了一种新的神经网络架构，称作Transformer。该架构只使用了attention机制（+MLPs），不需要RNN、CNN等复杂的神经网络架构，并行度高。

文章创新点包括：

提出了（Multi-Head Attention）机制，可以看成attention的ensemble版本，不同head学习不同位置不同的表示子空间的不同语义。
提出了Self-Attention，自己和自己做attention，使得每个位置的词都有全局的语义信息，有利于建立长依赖关系。这是因为Self-Attention是每个词和所有词都要计算 Attention，所以不管他们中间有多大距离，最大的路径长度也都只是 1，因此可以捕获长距离依赖关系。
Attention的抽象（应该也不算第一次在这篇文章中做的抽象）：文章将Attention抽象成q(query)、k(key)、v(value)三者的函数。即，首先根据q和k计算attention分配情况，然后根据分配的权重，对v进行加权，最后得到上下文向量。做个类比，q就是Decoder端$t$时刻的隐状态，k就是Encoder端$s$时刻的隐状态，v也是Encoder端s时刻的隐状态，但是这里的k和v只需要一一对应即可，不需要完全相等，因此一种变体的话，v可以是$\boldsymbol{x}_{\text{embedding}}+ \boldsymbol{h}_s$(加了个residual connection)

1. Encoder:

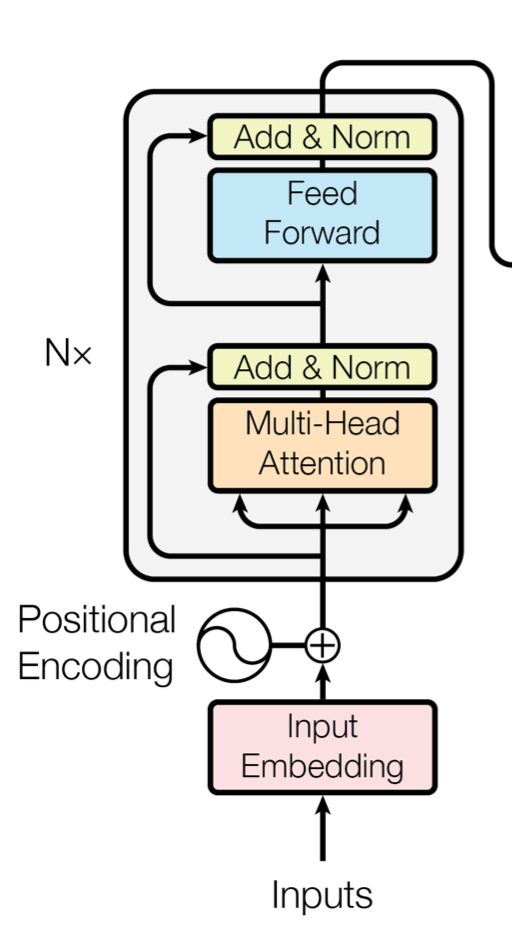
输入层：word embedding + position embedding。word embedding是常规操作。这里的position embedding是因为不使用RNN的话，位置信息就不能间接利用了，因此需要显示的对position进行embedding表示，即给每个位置一个向量化表达。作者使用正弦和余弦函数，使得位置编码具有周期性，并且有很好的表示相对位置的关系的特性（对于任意的偏移量$k$，$PE_{pos+k}$可以由$PE_{pos}$线性表示），同时模型可以拓展到那些比训练集中最大长度还大的未知句子的position表示（关于pos的函数）。
$$
PE(pos,2i)=sin(pos/10000^{2i/d_{\text{model}}}) \\
PE(pos, 2i+1)=cos(pos/10000^{2i/d_{\text{model}}})
$$
其中，pos是位置编号，$i$为embedding的第$i$维。记：$\boldsymbol{x}=\boldsymbol{x}_{\text{WE}}+\boldsymbol{x}_{PE} \in \mathbb{R}^{d_{model}}$，其中，${x}_{WE}$是输入词的word embedding，$\boldsymbol{x}_{PE}$是输入词的position embedding，$\boldsymbol{x}$是接下来Attention的输入。

输入的序列长度是$n$，embedding维度是$d_{model}$，所以输入是$n \times d_{model}$的矩阵$\boldsymbol{X}$。

Attention层：N=6，6个重复一样的结构(可以看出这里也是使用了多跳)，每种结构由两个子层组成：
- 子层1：Multi-Head self-attention
  
  源语句的self attention。Multi-Head Attention如下图右边所示，每个Multi-Head Attention包含了$h$个Scaled Dot-Product Attention组件，也就是每个Head就是一个Scaled Dot-Product Attention组件，如下图左边所示。
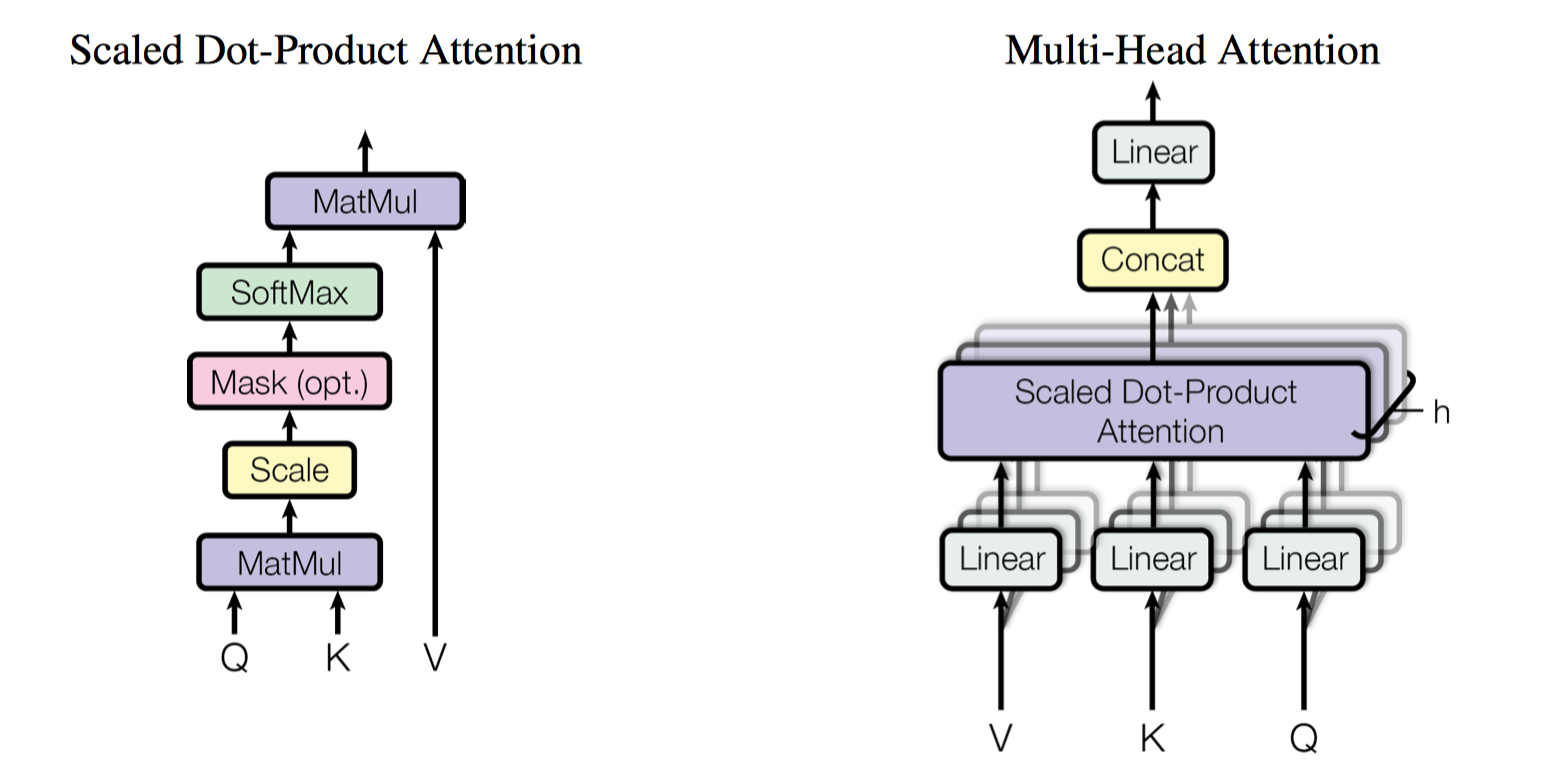
每个Head获取一种子空间的语义，多个Head可以看做是ensemble，且可以并行计算。对于一个Head，

a）首先，原始的$\boldsymbol{Q} \in \mathbb{R}^{n \times d_{model}}$、$\boldsymbol{K} \in \mathbb{R}^{n \times d_{model}}$、$\boldsymbol{V} \in \mathbb{R}^{n \times d_{model}}$先经过全连接进行线性变换映射成$\bar{\boldsymbol{Q}}=\boldsymbol{Q} \boldsymbol{W}_i^Q \in \mathbb{R}^{n \times d_k} , \bar{\boldsymbol{K}}=\boldsymbol{K} \boldsymbol{W}_i^{K} \in \mathbb{R}^{n \times d_k}, \bar{\boldsymbol{V}}=\boldsymbol{V} \boldsymbol{W}_i^{V} \in \mathbb{R}^{n \times d_v}$。

b) 接着，将映射后的$\bar{\boldsymbol{Q}}, \bar{\boldsymbol{K}}, \bar{\boldsymbol{V}}$输入到Scaled Dot-Product Attention，得到中间Attention值，记做，$\text{head}_i = \text{Attention}(\bar{\boldsymbol{Q}}, \bar{\boldsymbol{K}}, \bar{\boldsymbol{V}}) \in \mathbb{R}^{n \times d_v}$。对于$\text{Attention}$函数，先计算$\bar{\boldsymbol{Q}}$和$\bar{\boldsymbol{K}}$点乘相似性，并使用$1/\sqrt{d_k}$缩放，然后经过softmax激活后得到权重分布，最后再对$\bar{\boldsymbol{V}}$加权，即：$\text{Attention}(\bar{\boldsymbol{Q}}, \bar{\boldsymbol{K}}, \bar{\boldsymbol{V}})=\text{softmax}(\frac{\bar{\boldsymbol{Q}} \bar{\boldsymbol{K}}^T}{\sqrt{d_k}}) \bar{\boldsymbol{V}}$

c) 然后，将所有的中间Attention值concat在一起$\boldsymbol{C}=\text{Concat}(\text{head}_1, \text{head}_2,…, \text{head}_h) \in \mathbb{R}^{n \times hd_v}$，

d) 最后，再经过一个线性映射$\boldsymbol{W}^O \in \mathbb{R}^{hd_v \times d_{model}} $，得到最终输出的Multi-Head Attention值，$\text{Multi-Head}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})=\boldsymbol{C} \boldsymbol{W}^{O} \in \mathbb{R}^{n \times d_{model}}$，其捕获了不同表示子空间的语义。

综合起来，即：
$$
\text{Multi-Head}(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V})=\text{Concat}(\text{head}_1, \text{head}_2, …, \text{head}_h) \boldsymbol{W}^{O} \\
\text{where} \ \text{head}_i = \text{Attention}(\boldsymbol{Q} \boldsymbol{W}_i^Q , \boldsymbol{K} \boldsymbol{W}_i^K , \boldsymbol{V} \boldsymbol{W}_i^V) \\
\text{where} \ \text{Attention}(\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V})=\text{softmax}(\frac{\boldsymbol{Q} \boldsymbol{K}^T}{\sqrt{d_k}}) \boldsymbol{V}
$$
子层1的输出：$\text{O}^{\text{Encoder},1}=\text{LayerNorm}(X + \text{Multi-Head}(X))$，此时$\boldsymbol{Q}=\boldsymbol{K}=\boldsymbol{V}=\boldsymbol{X} \in \mathbb{R}^{n \times d_{model}}$。
- 子层2：
  
  position-wise 前馈神经网络。即上述输出的矩阵每一行代表相应位置的单词经过attention后的表示，每个位置的向量$\in \mathbb{R}^{d_{model}}$经过两层的前馈神经网络（中间接RELU激活）得到一个输出FFN。
  $$
  \text{FFN}(x) = max(0, xW_1+b_1)W_2+b_2, \forall x \in \{\text{O}^1_{1,*}, …,\text{O}^1_{n,*}\}
  $$
  上述参数所有位置共享，$F=\{\text{FFN}(x)\} \in \mathbb{R}^{n \times d_{model}}$。
  
  子层2的输出：$O^{\text{Encoder},2}=\text{LayerNorm}(O^{\text{Encoder},1}+F)$

Decoder：

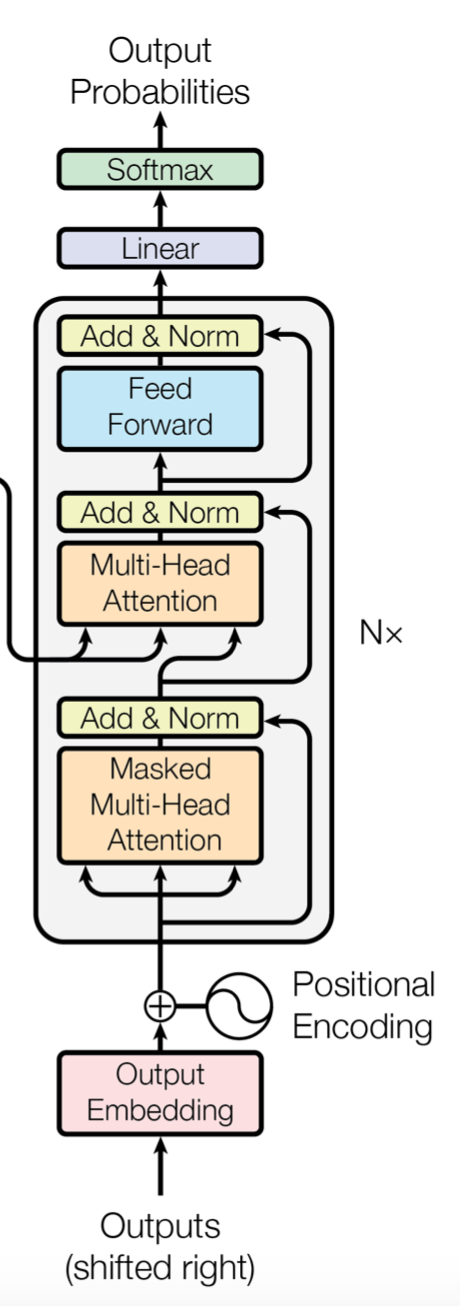
输入层：

已经翻译出的目标词word embedding+position embedding。结构同encoder中的输入层，每个单词embedding维度为$d_{model}$，假设已经翻译了$m$个词，则输入为矩阵$\boldsymbol{Y}\in \mathbb{R}^{m \times d_{model}}$。
Attention层：共6个。
- 子层1：Masked Multi-Head Self-Attention
  
  目标语句的self-attention，加了掩码的multi-head attention，防止目标语句中前面的单词attend到后面的单词，来维护自回归的性质。这和Encoder中不同，Encoder中没有加该限制。具体实现时，只需要在scaled dot-product Attention中，将softmax的输入中不合法的attend连接设置成无穷小即可(这样经过softmax后这些权重为0)。
  
  该层的输出同样采取Add和LayerNorm。
- 子层2：Multi-Head Attention
  
  前面两次用到的Multi-Head Attention都是源语句或目标语句各自内部的Attention。而该子层2是目标语句和源语句之间的Attention。此时，$\boldsymbol{Q}$是Decoder端的单词表示，即上述Masked Multi-Head Self-Attention得到的输出，$\boldsymbol{K}$， $\boldsymbol{V}$是Encoder端的输出，即前文所述的$O^{\text{Encoder},2}=\boldsymbol{K}=\boldsymbol{V}$。
  
  该子层允许目标语句每个词都能attend到源语句不同的单词上，且每个目标单词都能计算一个对应的上下文向量。该子层的输出$\in \mathbb{R}^{m \times d_{model}}$。
- 子层3：Position wise 前馈神经网络
  
  和Encoder中的一致。输出$\in \mathbb{R}^{m \times d_{model}}$。
输出层：

将上述依次经过6个Attention层的输出经过一个全连接层并softmax激活后得到下一个预测的单词的概率分布。

另外，Transformer比较好的文章可以参考以下两篇文章：一个是Jay Alammar可视化地介绍Transformer的博客文章The Illustrated Transformer ，非常容易理解整个机制；然后可以参考哈佛大学NLP研究组写的“The Annotated Transformer ”，代码原理双管齐下，很细致。

总之，这篇文章中提出的Transformer本质上是个叠加的自注意力机制够成的深度网络，是非常强大的特征提取器，尤其是在NLP领域。Transformer近几年也一跃成为踢开RNN和CNN传统特征提取器，荣升头牌，大红大紫。很多后续的NLP先进的研究工作都会基于Transformer展开。例如，词预训练工作上，18年OpenAI工作：Improving Language Understanding by Generative Pre-Training（GPT）和 18年Google AI Language工作：BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding （BERT），这两个重要工作都是基于Transformer特征提取器做的，其提出的两阶段训练方式（pre-training+fine-tuning）做迁移学习几乎刷爆了所有的NLP任务。

Summary

本文主要对基本的Attention机制以及Attention的变体方面的工作进行了梳理。我们不难发现Attention机制简单，优雅，效果好，沟通了输入和输出之间的联系，易于推广和应用到多种多样的任务和场景中，如计算机视觉，NLP，推荐系统，搜索引擎等等。除此之外，我们可以回顾下早期的一些奠基性的工作，注意力机制的好处在于很容易融入到其他早期的一些工作当中，来进一步提升早期成果，例如，将注意力机制引入到早期词预训练过程中，作为特征提取器，来提升预训练的效果，这在今年NLP工作中尤为突出（e.g.，BERT）。还比如，可以将注意力机制用于模型融合；或者将注意力机制引入到门限函数的设计中（e.g.，GRU中代替遗忘门等）。总之，Attention机制的易用性和有效性，使得很容易引入到现有的很多工作中，也很容易的应用到各种各样的实际业务或场景当中。另外Attention的改进工作包括了，覆盖率（解决重复或丢失信息的问题），引入马尔科夫性质（前一时刻Attention会影响下一时刻的Attention，实际上多跳注意力能够解决该问题），引入监督学习（例如手动对齐或引入预训练好的强有力的对齐模型来解决Attention未对齐问题）等等。