本文主要调研了两篇基于分离式表征(Disentangled Representation)的图神经网络文章。

ICML2019 | DisenGCN: Disentangled Graph Convolutional Networks：清华崔鹏老师团队的工作，基于分离式表征的图神经网络的奠基性工作。
SIGIR2020 | DGCF: Disentangled Graph Collaborative Filtering：中科大何向南团队的工作，分离式表征在推荐系统中的奠基性工作。

首先解释下Disentangled的概念。这个概念最早可以追溯到Bengio et al., 2013的文章 Representation Learning: A Review and New Perspectives，Disentangled可以翻译为分离式、解耦式或者解离式。与之对应的是Entangled，即：耦合式。参考ICML 2019 best paper中的论述：challenging common assumptions in the unsupervised learning of disentangled representations，目前非正式的定义如下：

分离式表征应当能够将蕴含在变化数据中的特定不变且有信息量的因子分离出来。 A disentangled representation should separate the distinct, informative factors of variations in the data.
表征向量中某些维度的取值只会随着与之对应的隐因子的变化而变化，而不会随着其它因子的变化而变化。Single latent units are sensitive to changes in single generative factors, while being relatively invariant to changes in other factors (Y. Bengio et al., 2013).
某个隐因子的变化应导致学习到的表征中该隐因子对应维度上的变化。A change in a single underlying factor of variation should lead to a change in a single factor in the learned representation (Locatello et al., 2019).

按照个人的理解来解读下上面三条非正式定义。第一条想表达的是变化的数据中总蕴含着一些不变的隐因子，是这些隐因子决定了真正的数据分布。即：真实数据实际上是由这些隐因子生成的，思想类似混合高斯分布，分离式表征目标是将这些隐因子解离出来。这一条实际上阐明了分离式表征的核心原理和假设，即：真实的观测数据是由两阶段的生成过程生成的。首先，会从一个分布$P(\boldsymbol{z})$随机抽取一个隐变量$\boldsymbol{z}$，该隐变量蕴含着原始数据中的某种语义；接着会基于该条件概率分布$P(\boldsymbol{x}|\boldsymbol{z})$采样生成真实的观测样本$\boldsymbol{x}$。这种生成模型的关键思想在于高维数据$\boldsymbol{x}$能够通过低维的隐语义因子$\boldsymbol{z}$来解释和映射生成。第二条想表达的是不同隐因子之间相互独立，表征向量中某些维度的取值只会受到对应的隐因子的变化的影响，对其它隐因子的变化鲁棒性高。第三条是对第二条的补充，分离式表征中的不同维度与不同隐因子之间有着映射关系，某个隐因子的变化会引起该分离式表征中对应的维度取值的变化。

总结一下，第一条指出了隐因子的重要性和分离式表征的核心原理和假设；第二条是隐因子的鲁棒性性质；第三条是隐因子和分离式表征之间的关系，隐因子应当能够各自独立地映射到分离式表征不同的维度上。

进一步阐述分离式表征的特点，仍然参考：ICML2019 Best Paper: Challenging Common Assumptions in the Unsupervised Learning of Disentangled Representations，

分离式表征必须以一种完备且可解释的结构来包含所有样本中的信息，这些信息是独立于手头的目标任务之外的。They should contain all the information present in $x$ in a compact and interpretable structure (Y. Bengio et al., 2013; X. Chen et al., 2016) while being independent from the task at hand.
分离式表征需要对下游的(半)监督任务，迁移学习任务，小样本学习任务等有效。They should be useful for (semi-)supervised learning of downstream tasks, transfer and few shot learning (Y. Bengio et al., 2013; Peters et al., 2017).
分离式表征能够挖掘出扰动因子，从而能够更好地进行人工干预和回答反事实问题。They should enable to integrate out nuisance factors (Kumar et al., 2017), to perform interventions, and to answer counterfactual questions (Peters et al., 2017).

总结一下，Distentangled的目的就是希望从低阶的观测数据中分离抽象出潜在(latent, underlying)、高阶的解释性因子 (explanatory factors)；而Disentangled Representation的目的是希望将分离出来的factors独立地映射到表征向量中不同维度的的latent units上。一方面，这样的表征能够融合多种的解释性因子，语义性和解释性更强；另一方面，不同因子之间独立性较强，某个因子的轻微扰动，不会对其它因子造成过多影响，鲁棒性较强；最后，如果某个task和某个factor高度相关，而与其它factor不相关时，分离式表征也能够更好地通过该相关的factor解决任务，适用性更强，有利于迁移学习和小样本学习。相反，Entangled Representation由于耦合了所有的factor，学习出来的Representation是高度依赖于特定任务的，且解释性不够强。

个人认为，目前主流的LDA，LSA，矩阵分解等方法，其实都是entangled representation，虽然不同隐维度能够表征一定的语义，但是不同维度之间实际上是耦合的，语义存在重叠，是目标任务导向的，在可解释性上比较牵强。Distentangled Representation希望能够将隐因子解耦开，学习到的表征中的不同部分能够反映不同隐因子，由于不同隐因子表达着不同的语义，因此学习到的表征的不同维度实际上蕴含着相互独立的语义，具备较强的可解释性，并且有利于迁移学习。

但是这里头值得强调的一点是，Disentangled Representation可以是任意形式的数据以及依赖于这个数据的问题抽象形式，它应该能够反映问题本身的一些内在结构。但是通常情况下，这样的抽象通常要建立在我们对数据的先验认知上，也即：具备归纳偏置(inductive bias)。比如graph图数据中，结点连边关系可能是受到某种潜在因子的约束，那么就可以用Distentangled Representation的方式来解离并表征这种潜在的因子。或者进一步通过监督信号来引导分离式表征的学习，此时才有可能学习到well-Disentangled的表征。这也是ICML2019 best paper的主要观点，数据或模型不具备归纳偏置时，无监督分离式表征是无法学习好的。下面要介绍的两篇文章都有引入监督信息，因此不在这个范畴里。

下面将展开介绍两篇在GNN领域应用分离式表征的文章。ICML 2019 DisenGCN 和 SIGIR 2020 DGCF。DisenGCN是基于分离式表征的图神经网络的奠基性工作；而DGCF借鉴了DisenGCN的思想，将分离式表征应用于图协同过滤中，也是分离式表征在推荐系统中的奠基性工作。

1. ICML 2019 | DisenGCN

1.1 Motivation

DisenGCN的动机主要是为了解决传统的GCN不能将潜在的因子解离开来进行节点表示学习的问题。也就是说传统的GCN方法都是Entangled，对邻居进行卷积形成耦合式表征，即：表征向量不同维度因子之间的语义是耦合的，忽略了不同维度对连边形成的影响程度可能是不同的，不仅容易模糊不同维度的语义边界，也很容易造成过平滑的表征。

为了将分离式表征用于图神经网络模型，作者认为图结构中的结点之间的连接方式是受到潜在的因子影响的，也就是说，不同的隐因子会造成不同的连边关系。在进行表征学习时，将造成节点连边的因子解离出来，并独立地映射到相对应的表征向量不同维度上，可以让模型更具有可解释性，学习到的表征对变化的适应性也更强，鲁棒性更强，泛化能力更好。

为了解决这样的问题，作者提出了一种创新的邻域路由机制 (neighborhood routing mechanism)，对某个结点，能够动态地识别出造成该结点与某邻域结点间连边关系的隐因子，并相应地将该邻居结点分配到该隐因子所属channel，通过该channel上的结点的卷积操作来形成与该隐因子相关的Distangled Representation。

1.2 Contribution

提出了DisenGCN，能够学习结点的Disentangled Representation。
提出了邻域路由机制，能够推断形成每条边的潜在因子，支持归纳式学习inductive learning。
理论上证明邻域路由机制的收敛性，并经验性地阐述Disentangled Representation的优势。

1.3 Solution

从总体上先梳理下整个方法。作者对于图数据的抽象和假设的点体现在，结点之间连边的形成可能受到多种潜在因子的影响。这个假设是符合我们对于图数据的先验认知的。现实世界中，各种各样的图，其连边拓扑结构是受到不同因素的影响而形成的。这种因素通常不容易显式地在数据中记录和表达出来，我们的目标是解离出这种潜在因子，并将这些潜在因子独立地映射到结点表征向量不同维度上，从而形成分离式表征，即表征的不同部分都对应着某种语义。

DisenGCN的输入是Graph $G=(V,E)$，每个结点$u \in V$有对应的特征向量$\boldsymbol{x}_u \in \mathbb{R}^{d_{in}}$。DisenGCN的目标是学习结点的分离式表征，即：
$$
\boldsymbol{y}_u=f(\boldsymbol{x}_u, {\boldsymbol{x}_v:(u,v) \in G })
$$
$f$看做是DisenGCN，输入是目标结点$u$的特征向量以及其邻域结点的特征向量，输出是$u$结点的分离式表征$\boldsymbol{y}_u \in \mathbb{R}^{d_{out}}$。其中，$\boldsymbol{y}_u$由$K$个独立的组件构成，即：$\boldsymbol{y}_u=[\boldsymbol{c}_1, \boldsymbol{c}_2,…,\boldsymbol{c}_K]$，$K$是要分离出来的隐因子数量，是超参数。$\boldsymbol{c}_k \in \mathbb{R}^{d_{out}/K}$是分离出来的第$k$个隐因子对应的表征组件，各组件的维度数假设相同。即：不同隐因子会各自独立地映射到表征向量的部分维度上，极端情况下，当$K=d_{out}$时，此时每个隐因子都映射到向量的一个维度上。可以看出，DisenGCN的核心目标就是学习出各个隐因子对应的表征，然后拼接在一起形成最终的分离式表征。

DisenGCN的核心组成：DisenConv layer的结构如下，DisenConv layer的输入为目标结点特征向量$\boldsymbol{x}_u$以及其邻域结点特征向量集合${\boldsymbol{x}_{v}}$，输出是该目标结点$u$的分离式表征。

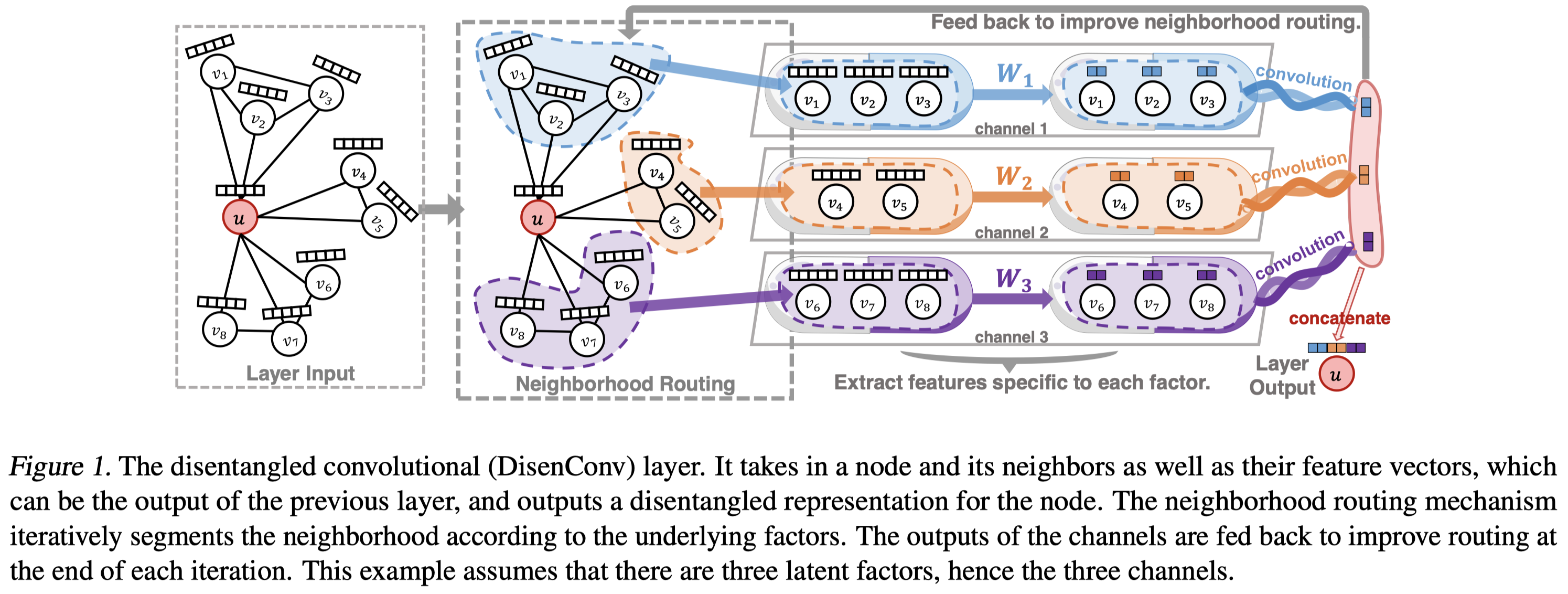
图中的隐因子数量超参数为3，即：3个通道。从隐因子的抽象语义来说，任意一个结点$u$可能是通过任意一种通道到达其邻居结点$v$的。因此，我们的目标是希望解离出形成每种连边关系的通道隐因子，将这种通道隐因子解离出来，并形成每个结点在每个通道下的分离式表征，最终的分离式表征是由这三种通道下的分离式表征拼接形成的，每段分离式表征衡量了结点在相应通道下的语义。

首先，每个邻居结点$v$对应的原始的特征向量会经过一个通道特定的参数映射矩阵$\boldsymbol{W}_k$映射到该通道$k$，并经过L2-norm，得到$v$结点该通道上的特征向量$\boldsymbol{z}_{v,k}$，称之为邻居结点$\boldsymbol{v}$在通道向量。
$$
\boldsymbol{z}_{v,k}= \text{norm}(\sigma(\boldsymbol{W}_k^T \boldsymbol{x}_v+ \boldsymbol{b}_k))
$$
每个结点都可以通过上述公式来得到初始的通道特定的向量。
接下来是卷积操作的迭代步骤，
- 计算映射后的【邻居结点$v$通道向量$\boldsymbol{z}_{v,k}$】和【我们要求的目标结点$u$通道向量$\boldsymbol{c}_k$】之间的亲和度，softmax转成一个定义在所有通道上的概率分布$p_{v,k}$，衡量了$u$结点通过$k$通道到达邻居结点$v$，从而形成该连边的概率。
$$
p_{v,k}^{(t-1)}=\text{softmax}(\boldsymbol{z}_{v,k}^T \boldsymbol{c}_k^{(t-1)}/\tau)= \frac{\exp(\boldsymbol{z}_{v,k}^T\boldsymbol{c}_k^{(t-1)}/\tau)}{\sum_{k^{\prime}=1}^K \exp(\boldsymbol{z}_{v,k^{\prime}}^T{\boldsymbol{c}_{k^{\prime}}}^{(t-1)}/\tau)}
$$

$\boldsymbol{c}_k^0$使用上述公式，即$\boldsymbol{z}_{u,k}$来初始化。
- 根据该概率分布来更新目标结点$u$的通道向量$\boldsymbol{c}_k^{(t)}$。
$$
\boldsymbol{c}_k^{(t)}=\text{norm}(\boldsymbol{z}_{u,k}+\sum_{v:(u,v) \in G} p_{v,k}^{(t-1)}\boldsymbol{z}_{v,k})
$$

$t$是迭代次数，上述两个步骤可以反复迭代多次。上述更新过程非常像EM算法。实际上，作者在证明上述路由机制的收敛性的时候就用到了EM算法来证明。做个类比，$\boldsymbol{c}_k^{(t)}$是$k$通道下的聚类中心$u$，与$u$结点相连的邻居结点是属于该聚类簇里的结点，需要根据这些结点来不断更新聚类中心向量，更新的方式是看这些邻居结点在$k$通道下与$u$结点的亲和度值，根据该亲和度值来加权更新。

另一方面，又很像GATs中的注意力机制，$p$就像是注意力分数的概率分布，只不过GATs中的注意力概率分布是定义在所有邻居结点上的；而此处的p是定义在所有通道上的概率分布。通过上述路由过程，能够把和连边相关的因子解离出来，并通过这种soft形式的亲和度来加权形成分离式表征。

对每个通道$k$，都执行上述过程，从而形成一阶的分离式表征，$\boldsymbol{y}^{(1)}_u=[\boldsymbol{c}_1^{(1)}, \boldsymbol{c}_2^{(1)},…,\boldsymbol{c}_K^{(1)}]$。这个过程是1层DisenConv layer输出的。

为了捕获多阶的结点关系，叠加多层DisenConv layer，从而形成多阶的分离式表征，递推公式即：
$$
\boldsymbol{y}_u^{(l)}= \text{dropout}(f^{(l)}(\boldsymbol{y}_u^{(l-1)}, {\boldsymbol{y}_v^{(l-1)}:(u,v) \in G }), 1 \leq l \leq L
$$
作者此处的下游任务是多分类，因此在$\boldsymbol{y}_{u}^{(L)}$后面接一层全连接层。即：$\boldsymbol{y}_{u}^{(L+1)}={\boldsymbol{W}^{(L+1)}}^T \boldsymbol{y}_u^{(L)}+\boldsymbol{b}^{(L+1)}$。

如果每个样本的分类标签只可能有1种，就使用多分类交叉熵损失来训练。即：
$$
-\frac{1}{C}\sum_{c=1}^C \boldsymbol{y}_u(c) \ln (\hat{\boldsymbol{y}}_u(c))
$$
其中，$\hat{\boldsymbol{y}}_u(c)=\text{softmax}(\boldsymbol{y}_{u}^{(L+1)})$。

如果每个样本的分类标签有可能多取值，就使用多个二分类损失来训练。即：
$$
-\frac{1}{C}\sum_{c=1}^C [\boldsymbol{y}_u(c) \text{sigmoid}(\boldsymbol{y}_{u}^{(L+1)}(c)) + (1-\boldsymbol{y}_u(c)) \text{sigmoid}(-\boldsymbol{y}_{u}^{(L+1)}(c))]
$$
注意，$\boldsymbol{y}_u(c)$和$\text{sigmoid}(\boldsymbol{y}_{u}^{(L+1)}(c)$都是向量。

1.4 Summarization

作者把要解离的因子定义和抽象在结点与结点之间的连边关系上，认为不同的因子对连边形成的影响程度是不同的。因此可以将邻居卷积分通道来卷积，这样可以分离出和通道相关的该隐因子对应的表征。想法挺巧妙的，实践中是否真正有效，有待验证。另外，不同连边因子稀疏性可能不太一样，有的可能过分稀疏，强行给每种连边关系都提高影响力可能会造成有些因子并不能很好地学习到。而这种情况下，感觉耦合式表征能更好地学习，因为其它因子也可以一定程度上迁移到稀疏因子上，所有因子之间是互帮互助的。最后，作者开篇提到不同因子之间是独立的，但是实际上该方法理论上无法保证不同因子是独立的，文中也没有通过某些独立性约束来达到该目的。因此，可能学习到的表征并不是weill-disentangled，不同因子间可能仍然存在着较大的联系。最后，对于语义直觉上的刻画和实验比较欠缺，这些隐因子具体对应于观测数据中的哪些语义，是什么样的映射关系，是需要探究的。

2. SIGIR2020 | DGCF

这篇文章是何向南老师的团队发表在SIGIR2020上的一篇关于分离式图协同过滤的推荐方法，将分离式表征和GNN结合在一起，应用于二分图建模和推荐上。

2.1 Motivation

用户对物品的交互意图是多种多样的，传统的图神经网络没有加以区分，假定了所有user和item之间的交互关系是无差别的。导致的问题是：学习到的嵌入表示是次优的，且无法建模多种多样的交互关系，发掘出细粒度的用户意图。disentangle纸面上含义是解开。也就是说，对于传统方法，学习到的表征只蕴含着粗粒度的user-item交互意图，也即意图是纠缠在一起，未解开的，因为模型并没有显式地去建模和挖掘这种细粒度的意图。disentangle的目的是希望去挖掘和解开用户的意图，使得学习到的表征能够表达出用户多种多样的意图，并且能够将该意图映射到用户的表征上。这样的表征称为：disentangled representations. 因此本文提出了DGCF (Disentangled Graph Collaborative Filtering) 方法，去建模每对user-item交互关系上用户的隐意图分布，并将该隐意图映射到表征上，从而形成分离式表征。可以看出，本文作者应用分离式表征在GNN上，其对图数据内在结构的抽象依然是建立在结点连边关系上，和DisenGCN类似，认为结点之间之所以能够形成连边，是受到一些潜在的因子影响的，具体的，在基于二分图的推荐系统上，这种因子从语义上反映了用户多种多样的交互意图。

2.2 Contribution

阐明了协同过滤中用户和物品之间多样的交互关系的重要性，建模这种多样的关系对于学习到更好的表征和提高模型的解释性都有很大的帮助。
提出了DGCF模型，细粒度地考虑了user-item间的交互意图并映射到最终的分离式表征disentangled representations。
做了广泛的实验，在各种benchmark数据上均胜出，推荐性能、对隐用户交互意图的发掘、解释性方面都表现出色。

2.3 Solution

先从整体上梳理DGCF。整个方法仍然遵循着基于消息传递机制的GNN那套框架，如NGCF。在NGCF中，任意user-item边的类型没有区分对待。而在DGCF中，我们的目标是从用户细粒度的意图角度来探索任意user-item连边关系形成的原因；并基于探索到的意图来生成分离式表征。从直觉上来举例，这种意图可能是用户为了消遣时间，才选择交互某个物品；也可能是为了给家人购物，才选择交互某个物品等等。不同的意图对用户交互行为产生的贡献度是不同的。挖掘出这种细粒度的意图，并独立地映射到最终的分离式表征向量上，使得表征向量的不同维度能够反映不同的用户意图，是本文的重点目标。当然，从本质上来说，本文所说的意图仍然是潜在、隐式的意图，刻画的真实语义需要通过实验来观察。

为了挖掘出细粒度的用户意图，作者首先将最终的表征向量划分成多个chunk，每个chunk独立地与某种待挖掘的意图关联起来，因此需要针对每种意图，来形成意图感知的chunk表征，最终的分离式表征则由所有的chunk表征拼接而成。那么问题的关键在于如何发掘潜在的意图以及如何基于挖掘的意图生成分离式表征。

1.首先，针对意图的挖掘，作者将意图隐因子抽象在图数据中的连边关系上，建模每条连边在所有$K$个意图上的概率分布：$\boldsymbol{A}(u,i)=(A_1(u,i), A_2(u,i), …, A_K(u,i))$。$A_k(u,i)$表示第$k$个意图促使用户$u$交互$i$的置信度，即连边$(u,i)$形成的置信度。$A$可以看作是邻接矩阵。邻接矩阵$A_k$的某个单元$(u,i)$取值非零，则代表用户$u$交互了物品$i$，其取值反映了意图$k$促成此次交互行为的置信度。因此，$K$个意图的话，就会有$K$个邻接矩阵，该邻接矩阵的取值会在训练的过程中不断调整，直至收敛，也即邻接矩阵是可变的。针对$K$个邻接矩阵的同一个单元$(u,i)$，最终的取值即为每种意图对该条连边形成的贡献度，通过横向比较所有邻接矩阵同一个单元取值大小就可以看出每种意图对同一个交互行为的影响力了。

2.其次，针对分离式表征的生成，每个邻接矩阵都对应着一个sub-graph，$A_k$则对应着意图$k$下的用户物品二分图，我们称之为意图感知的加权子图，即：intent-aware weighted sub-graph。所有$K$个sub-graph的结点以及连边拓扑结构完全一样，差异只在连边的权重不一样。因此，意图$k$对应的分离式表征可以通过在对应的intent-aware weighted sub-graph上，使用GNN来提取。由于所有意图子图的结点和连边关系都相同，为了体现差异性，关键点就在于连边权重如何纳入GNN卷积过程中 (下文会提到, 通过消息传递机制中的decay系数)。

上述两个步骤会纳入一个统一的迭代框架下，也是1层Graph Disentangling Layer的核心过程，

1.首先，通过$K$个邻接矩阵对应的意图sub-graph来提取$K$个意图下的chunk表征。

2.接着，每种意图sub-graph下，每条连边对应的两个结点使用步骤1提取到的chunk表征之间的亲和度来动态调整和提炼新的连边权重，即邻接矩阵的取值会发生变化。

上述两个步骤不断迭代 (类似EM算法)，比如，接着步骤2，基于改变了权重后的意图sub-graph，进一步来进行GNN卷积生成新的意图chunk表征，然后继续基于新的chunk表征来调整连边权重。周而复始。

当然，在表征学习的过程中，作者还施加了一些chunk表征之间的独立性约束等条件，从而使得学习到的表征更well-disentangled。

总之，我们应当先明确DGCF的输入：user-item 交互二分图；输出：目标产物，即user和item的分离式表征；随机初始化的0阶表征是唯一可训练参数，除此之外，在训练的过程中，中间产物，即每个意图对应的邻接矩阵也是可变的 (通过表征向量之间的亲和度来表示，即：邻接矩阵的取值是关于表征向量的函数，因此邻接矩阵并不是训练参数)。

2.3.1 Framework

了解了整个方法的大体思路后，DGCF方法整体上还是比较简洁的，我们先来看DGCF的框架图：

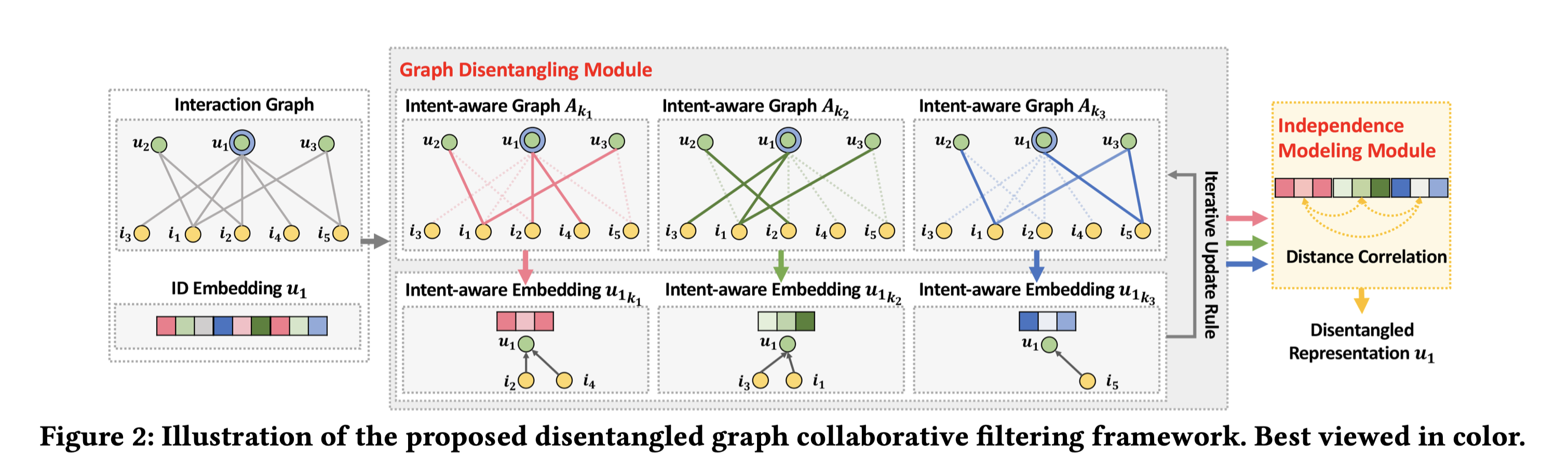
最左侧是原始的user-item交互二分图以及用户的ID embedding；ID embedding($d$维)根据latent intent factor的数量(e.g., $K$个)，平均切成$K$ chunk，每个chunk的embedding size为$d/K$，每个chunk embedding $\boldsymbol{e}_{ku} \in \mathbb{R}^{d/K}$对应一种意图$k$。所有的chunk embedding拼接形成最终的表征向量，即：$\boldsymbol{e}_u=(\boldsymbol{e}_{1u},\boldsymbol{e}_{2u},…,\boldsymbol{e}_{Ku})$。即：每个chunk embedding会各自独立地映射到最终的表征向量部分维度上。物品侧同理。

中间部分，每种意图$k$都对应一个intent-aware weighted sub-graph $\mathcal{G}_k$，也可用邻接矩阵$\boldsymbol{A}_k$来表示，该sub-graph用于提取用户和物品的chunk embedding，即 $\boldsymbol{e}_{ku}$和$\boldsymbol{e}_{ki}$。不同的sub-graph连边关系和原图一样，权重是可变的，在迭代中不断调整。在下文中的Graph Disentangling Module中会进一步介绍。

2.3.2 Graph Disentangling Module

意图是隐因子latent factor，每个意图对应一个intent-aware的带权交互子图，边的权重是动态调整的，会随着迭代的进行，来不断提炼(refine)。针对每个意图子图，迭代的过程大致如下：意图子图→基于消息传递的GNN邻域汇聚→形成子图对应的chunk表征→基于表征间的亲和度调整该子图连边权重→对调整后的子图继续使用基于消息传递的GNN邻域汇聚→形成新的子图对应的chunk表征→基于新的表征间的亲和度继续调整子图连边权重→……；周而复始，不断迭代直到收敛。

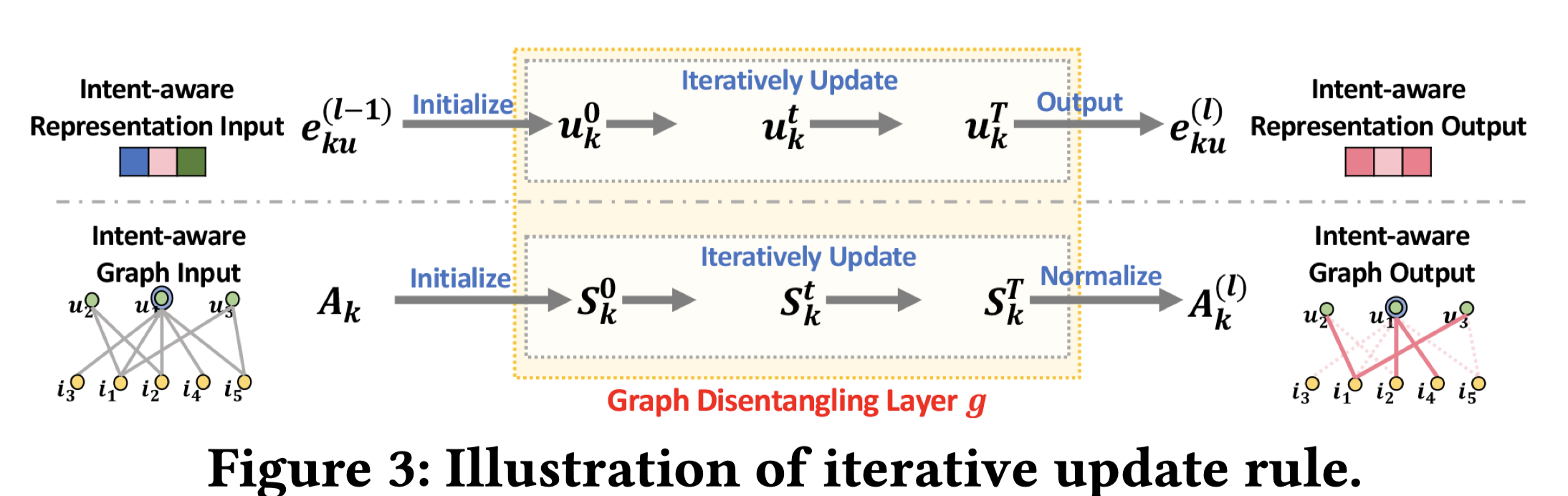
(1) Intent-Aware Initialization

前面Solution的开篇提到了，本文中唯一可训练对象是目标产物的分离式表征，但是中间产物意图邻接矩阵也是随着迭代的进行不断变化的。因此二者都要进行初始化。只不过意图邻接矩阵的初始化是用常数来初始化的，随着迭代的进行，其取值是关于表征向量的函数。

首先需要对用户的chunk embedding $\boldsymbol{e}_{ku}^{(0)}$进行初始化。记随机初始化的embedding向量为：$\boldsymbol{u}=(\boldsymbol{u}_1,…,\boldsymbol{u}_K)$。也即：$\boldsymbol{e}_{1u}^{(0)}=\boldsymbol{u_1},…,\boldsymbol{e}_{Ku}^{(0)}=\boldsymbol{u_K}$。$(0)$代表0阶。每个意图下的chunk embedding都是各自独立地进行随机初始化，这样能够保证不同的chunk embedding在开始训练的时候就存在比较大的差异。

同理，每个意图子图中的连边的权重或者说邻接矩阵的值，也要进行初始化。记连边$(u,i)$在所有$K$个意图子图下的权重构成的向量为：$\boldsymbol{S}(u,i)$，则初始时，默认所有子图下该连边的权重都为1，即：$\boldsymbol{S}{(u,i)=(S_1(u,i),…,S_K(u,i))=(1,…,1)}$，代表迭代开始的时候，所有的意图促成某个交互行为的贡献度是一样的，。

(2) Graph Disentangling Layer

下面都以用户为例，来介绍用户分离式表征提取的整个过程。物品侧是对称的，同理可得。首先来看单独一层Graph Disentangling Layer的输入与输出，
$$
\boldsymbol{e}_{ku}^{(1)}=g(\boldsymbol{u}_k, {\boldsymbol{i}_k| i \in \mathcal{N}_u})
$$
输入为用户$u$在意图$k$下的初始化表征 $\boldsymbol{u}_k$以及用户的邻域结点集合$\mathcal{N}_u$中物品的初始化表征$\boldsymbol{i}_k$，输出是一阶的用户分离式表征。

接下来是本文的重点和亮点，即：分离式表征提取的过程，涉及开篇提到的迭代过程。记迭代的总步数为$T$。此处要强调下，这里头涉及两个迭代的步数符号，一个是Graph Disentangling Layer层数，也即我们所熟悉的GNN的阶数，用带括号的$(l)$符号表示第$(l)$阶，总共的层数用$L$表示；另一个是，某一个Graph Disentangling Layer的内部，我们有一个迭代步数$t$，总共的步数为$T$（不带括号），代表提取某个意图$k$的分离式表征时所需要的迭代步数。下面介绍某个意图$k$的分离式表征的迭代过程。初始迭代时，分离式表征为：$\boldsymbol{u}_k^0, \boldsymbol{i}_k^0$，对第$t$步，

针对每条连边$(u,i)$，根据$K$个意图子图下的权重构成的向量$\boldsymbol{S}(u,i)$，进行跨意图的归一化，转成概率分布，来衡量不同意图对于该连边形成的贡献度，即：
$$
\hat{S}_k^t(u,i)= \text{softmax}(S_{k}^t(u,i))=\frac{\exp(S_{k}^t(u,i))}{\sum_{k^{\prime}=1}^K \exp S_{k^{\prime}}^t(u,i)}
$$
接着根据$\hat{S}_k^t(u,i)$计算消息传递时的decay系数，用于衡量在意图子图$\mathcal{G}$中，从$i$结点传递信息到$u$结点时的信息折扣比例，
$$
\mathcal{L}_k^t(u,i)=\frac{\hat{S}_k^t(u,i)}{\sqrt{D_k^t(u) \cdot D_{k}^t(i)}}
$$
其中，$D_k^t(u)=\sum_{i^{\prime} \in \mathcal{N}_u} \hat{S}_k^t(u,i^{\prime})$，$D_{k}^t(i)=\sum_{u^{\prime} \in \mathcal{N}_i} \hat{S}_k^t(u^{\prime},i)$。第一次迭代的时候，$D_k^t(u),D_k^t(i)$即分别为结点$u$和$i$的度。这个和NGCF论文中的衰减系数是类似的。
结点信息汇聚和更新：基于该系数来进行消息传递。值得注意的是，作者在做目标结点信息更新的时候，没有使用目标结点本身的信息，而只用了邻域汇聚到的信息来更新目标结点（结点0阶的表征在最后做layer combination有用到）。
$$
\boldsymbol{u}_k^t=\sum_{i \in \mathcal{N}_u} \mathcal{L}_k^t(u,i) \cdot \boldsymbol{i}_k^0
$$
使用$t=0$时的初始表征$\boldsymbol{i}_k^0$来表示要传递的信息。随着迭代步$t$的增加，要传递的信息保持不变。
意图$k$对应的邻接矩阵权重值的更新：基于更新后的表征，重新计算在意图$k$下，每条连边$(u,i)$中$u$和$i$结点之间的亲和度值，即：更新意图$k$对于这条连边形成的贡献值，这就是所谓的refine sub-graph的过程。
$$
S_{k}^{t+1}(u,i)=S_k^t(u,i)+{\boldsymbol{u}_k^t}^{\text{T}} \text{tanh}(\boldsymbol{i}_k^0)
$$

紧接着，基于更新后的邻接矩阵，继续重新开始迭代$t+1$步。上述4个步骤构成1个完整的迭代步，重复迭代至T步，就能够得到单层Graph Disentangling Layer输出的该意图$k$的分离式表征，也即1阶的分离式表征，即：
$$
\boldsymbol{e}_{ku}^{(1)}=\boldsymbol{u}_k^T
$$
作为副产物，一阶的邻接矩阵为：$\boldsymbol{A}_k^{(1)}=\hat{S}_k^T$，这个邻接矩阵蕴含着很丰富意图语义信息，能够用来做可解释性，在实验案例分析一节会用到。所有的$K$个意图都经过上述步骤，就能够形成一阶的分离式表征：$\boldsymbol{e}_u^{(1)}=(\boldsymbol{e}_{1u}^{(1)},\boldsymbol{e}_{2u}^{(1)},…,\boldsymbol{e}_{Ku}^{(1)})$

上述Graph Disentangling Layer叠加$L$层，就能够输出$L$阶的分离式表征，$\boldsymbol{e}_u^{(L)}$。层之间的递推式为：
$$
\boldsymbol{e}_{ku}^{(l)}=g(\boldsymbol{e}_{ku}^{(l-1)}, {\boldsymbol{e}_{ki}^{(l-1)}| i \in \mathcal{N}_u})
$$
按照我的理解，副产物$A_{k}^{(l)}$也会作为第$(l+1)$个卷积层的初始邻接矩阵来迭代，而不是对邻接矩阵重新赋值为全1来初始化。这一步文中没有强调，需要通过代码来佐证。

最终用户和物品的表征，作者采用了sum pooling的方式来对所有层输出的分离式表征做一个sum pooling，即：
$$
\begin{aligned}
\boldsymbol{e}_{ku}=\boldsymbol{e}_{ku}^{(0)}+…+\boldsymbol{e}_{ku}^{(L)} \\
\boldsymbol{e}_{ki}=\boldsymbol{e}_{ki}^{(0)}+…+\boldsymbol{e}_{ki}^{(L)}
\end{aligned}
$$

2.3.3 Independence Modeling Module

每个子图都会各自独立地提取对应的intent-aware representation；所有子图对应的chunk representation拼接在一起形成最终的disentangled representations. 为了使得每种意图之间互相独立，高度浓缩和蒸馏出和该意图最相关的信息，作者还提出了一种独立性建模模块。目标是希望不同意图子图得到的chunk representation之间相互独立。为此，作者采用了协方差相关性损失函数，称为independence loss：
$$
loss_{ind}=\sum_{k=1}^K \sum_{k^{\prime}=k+1}^K \text{dCor}(\boldsymbol{E}_k, \boldsymbol{E}_{k^{\prime}})
$$
$\boldsymbol{E}_k \in \mathbb{R}^{(M+N) \times (d/K)}$由意图$k$下的用户和物品表征拼接而成的矩阵。$dCor$为协方差，即：$\text{dCor}(\boldsymbol{E}_k, \boldsymbol{E}_{k^{\prime}})=\frac{\text{dCov}(\boldsymbol{E}_k, \boldsymbol{E}_{k^{\prime}})}{\text{dVar}(\boldsymbol{E}_k)\text{dVar}(\boldsymbol{E}_{k^{\prime}})}$。

最终，模型使用BPR Loss和independence loss这两个损失。且优化的时候，这两个损失是交替优化的。而不是相加起来同时优化。

2.4 Evaluation

2.4.1 对比实验

MF，GC-MC（KDD2019)，NGCF (SIGIR2019)，DisenGCN (ICML2019)，MacridVAE (NIPS 2019)。MF矩阵分解是最基本的baseline；GC-MC和NGCF是最近两年来比较流行的二分图协同推荐模型；DisenGCN和MacridVAE是基于分离式表征的方法。

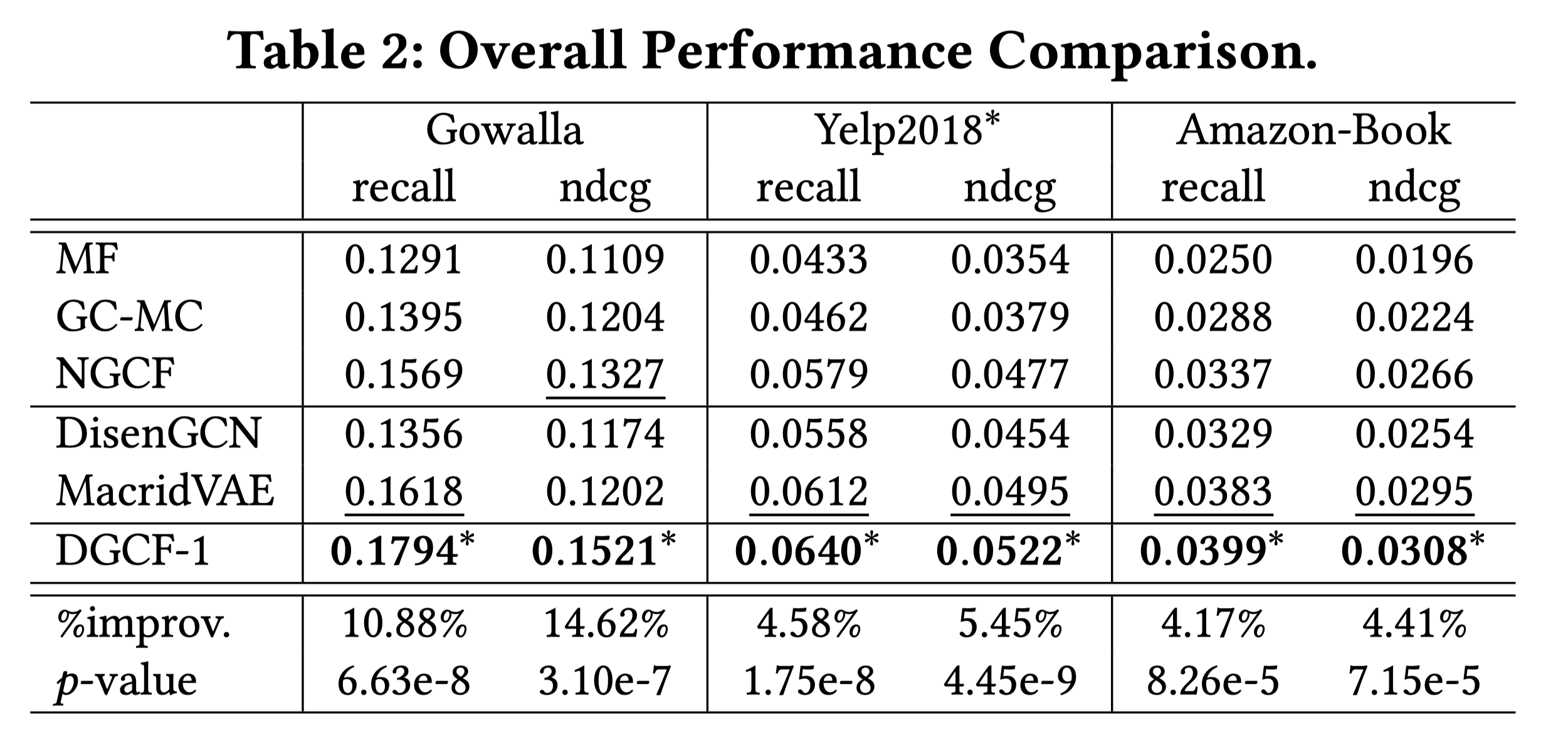
可以看出，在3个公开数据集上，模型简直完虐其它方法，还是很给力的。最大的亮点在于，DGCF相比于NGCF和LightGCN等，没有引入任何额外的参数（不同意图的chunk表征的维度是从完整表征维度中平均分配而来的），相当于在相同参数量的情况下，提升了模型的泛化能力。

2.4.2 参数实验

对于阶数，可以看出，DGCF叠加多层时，效果变好，说明对过度平滑的问题有一定的应对能力。

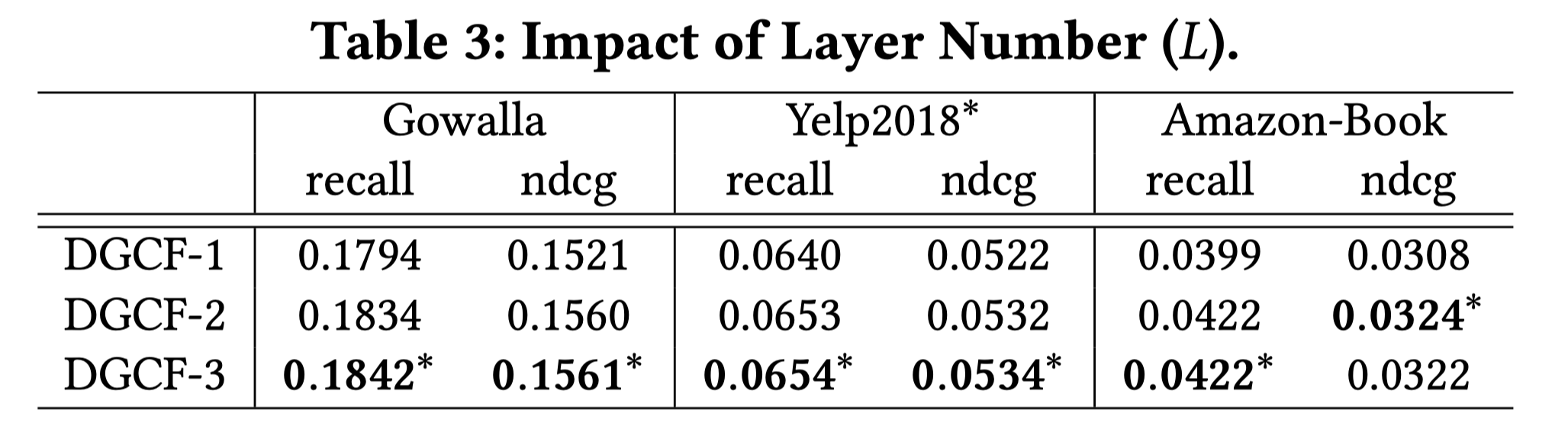
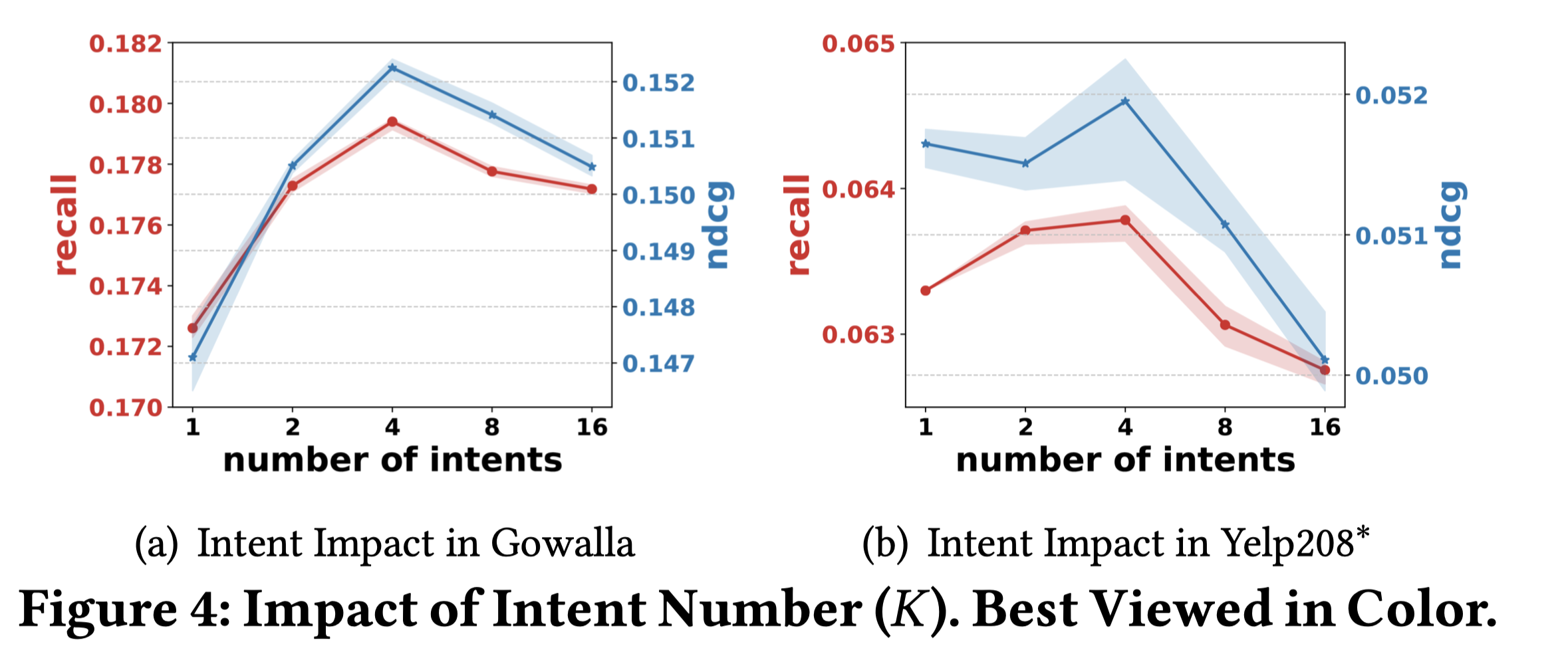
对于意图个数，可以看出，总体上意图在4个的时候最好。

对于独立建模模块，可以看出，有一定的影响，但是影响的程度其实很小。关键的提升在于Graph Disentangling Layer。

2.4.3 案例分析

案例分析主要的目的是希望观察学习到的分离式表征是否真正具备语义。采用了Yelp2018数据集，从其辅助信息review中来观察语义。

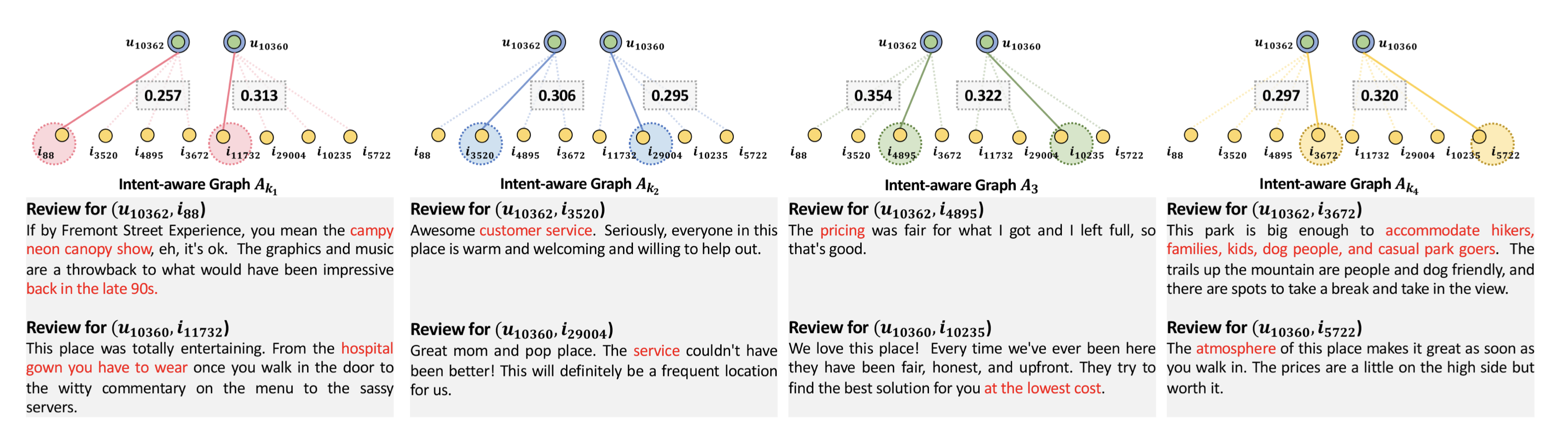
随机抽取了两个用户$u_{10362}$和$u_{10360}$，对最终学习到的意图邻接矩阵(对应意图子图)，观察某个用户的所有物品交互历史中，哪个分数最高，就用这个交互行为来代表这个意图的语义。比如在意图$k_1$对应的邻接矩阵中，用户$u_{10362}$交互物品$i_{88}$的意向分数最大，即邻接矩阵第10362行中，第88列的取值最大，就用第88列对应的物品的review来刻画这个意图$k_1$的语义；同理，用户$u_{10360}$ 交互的物品$i_{11732}$的review也可以用来刻画这个意图$k_1$的语义，通过纵向对比这两个物品的辅助信息，来观察意图对应的实际语义。例如：从图中可以看出，第一个交互意图的语义是用户独特的兴趣，第二个交互意图的语义是服务，第三个交互意图的语义是价格，第四个交互意图的语义是消遣。

这个案例分析还是比较有意思的，直观上来感受分离式表征的语义。

2.5 Summarization

这篇文章引入了分离式表征到GNN模型中，是对ICML 2019文章DisenGCN很好的拓展。在推荐任务中也表现的很好，是可解释性推荐系统重要工作之一。文章的code也相应地开源了，因此很值得借鉴和实践一下。不过也存在一些疑惑，比如：

参数量不变的情况下，引入了意图隐因子来建模意图，从而达到指标的提升，非常nice。问题是，这么多子图卷积操作，复杂度是不是会提高？
隐式的意图关系固然好；但是现实中，我们还可以收集到显式地意图关系，比如点击，收藏，购买等等，这些关系如何更好地融合和建模值得思考。

基于分离式表征的图神经网络调研