这篇文章主要介绍周国睿大佬的新工作：CAN: Revisiting Feature Co-Action for Click-Through Rate Prediction ^[1]。这个工作提供了一种新的特征交互思路，在特征工程上手动特征交叉和模型上自动特征交叉之间做了折衷，也是记忆性和泛化性的互补。可以认为是开创了特征交互的新路线。

欢迎关注我的公众号”蘑菇先生学习记”，更快更及时地获取关于推荐系统的前沿进展！

为了解释这两句话，我们不妨从一个简单的例子入手来理解。

假设我们的问题是预测用户是否会点击化妆品广告。显然，在这一场景下，根据我们的先验知识，年轻的女性更倾向于点击化妆品，因此：年龄和性别可以看做是一对Co-Action特征，对目标label的预测有显著的影响。

第一类迭代路线，很自然的想法，人工构造年龄和性别的交叉特征sex & age，比如：sex取值男性和女性，age分段。通过笛卡尔积，可以构造出很多组合交叉特征，如：”女性&18~25岁”，”男性&18~25岁”等。每个组合特征都单独进行嵌入表示，并独立地从数据中学习到这些嵌入。所谓的独立，可以从两个方面来理解。特征标识独立性上，”女性 &18~25岁”和”女性”以及”18~25岁”分别用三种不同的符号来唯一标识，在构造完特征后，三者之间是完全独立的；学习独立性上，只有同时满足”女性且18~25岁”的样本才能影响该交叉特征嵌入的学习，不会受到诸如”女性且30~40岁样本”或者”男性且18~25岁样本”的影响。

这种人工特征交叉拥有对数据的强记忆性优点。举个极端的例子，只要同时满足”女性”和”18~25岁”这两个条件的用户都会点击化妆品，不同时满足的用户都不会点击化妆品。那么就可以构造”女性&18~25岁”这个交叉特征，且只需要为该交叉特征设置1维的嵌入(等价于单变量线性模型$wx$中的$w$参数)，取值为正无穷大，那么sigmoid激活后预测交互概率肯定接近1，相当于通过1维的嵌入就能够记住整个数据中蕴含的规律。但是问题是，实际情况没有这么简单，通过这种方式会产生大量稀疏的特征，复杂度高，学习困难，迭代负担重，有大量组合特征的缺乏充足的样本来学习，导致学习过程不置信和不稳定。这也是传统逻辑回归用于手工特征交叉建模的主要问题所在。

第二类迭代路线，为了解决这一问题，涌现了FM/DeepFM/PNN等大量工作，通过模型来实现特征的自动交叉。即：两两交叉特征通过单一特征的嵌入之间的点积或外积等方式来间接表达。例如：”女性&18~25岁”这个交叉特征通过”女性“的嵌入和”18~25岁”的嵌入之间的点积来间接表达，并且这个交叉特征嵌入并不是直接且独立地从数据中学习来的，而是通过”女性”这一嵌入和”18~25岁”这一嵌入来间接表达和学习的，显然会受到单一的女性样本或者单一的18~25岁样本的影响，即不是独立学习的。虽然解决了稀疏性问题，带来了一定的泛化性，但是在一些Co-Action非常强烈的场景中，这样的泛化可能是过度的。比如在上面这个例子中，假设样本中有大量的”18~25岁男性样本”，根本不想点化妆品，但是在第二类迭代路线中，这类样本会影响”18~25岁”这一特征嵌入的学习，导致可能带偏”女性&18~25岁”这一交叉特征的表达。相反，在第一类迭代路线中，就不存在这样的影响。因此，模型层面的交叉，如果不涉及到独立交叉特征嵌入的学习，本质上都是伪交叉^[3]，可能学不好高阶的交叉信息。

那么如何在上述两大类迭代路线之间做一个折衷，做到既有很强的记忆性，又不会过度泛化呢？CAN提供了一种新的思路和迭代路线。核心目的是让Co-Action的建模过程中有相对比较稳定和独立的参数来维持对建模信息的学习记录，同时又想让不同的Co-Action间有一定的信息共享^[2]。个人认为，前者体现了记忆性，让交叉特征能够比较独立的学习，有效建模co-action特征；后者体现了泛化性，能够控制模型的参数复杂度，通过一定的信息共享来提高学习的泛化能力。

1. Motivations

首先介绍下Co-action特征的概念。Co-action指的是特征之间的协同效应，对于目标的预测有显著的影响。比如：在电商场景下，用户最近一次历史点击item和目标item就是一对很强的Co-action特征，对于预测用户是否会点击目标item非常有帮助。也可以从图的视角来理解Co-action特征。

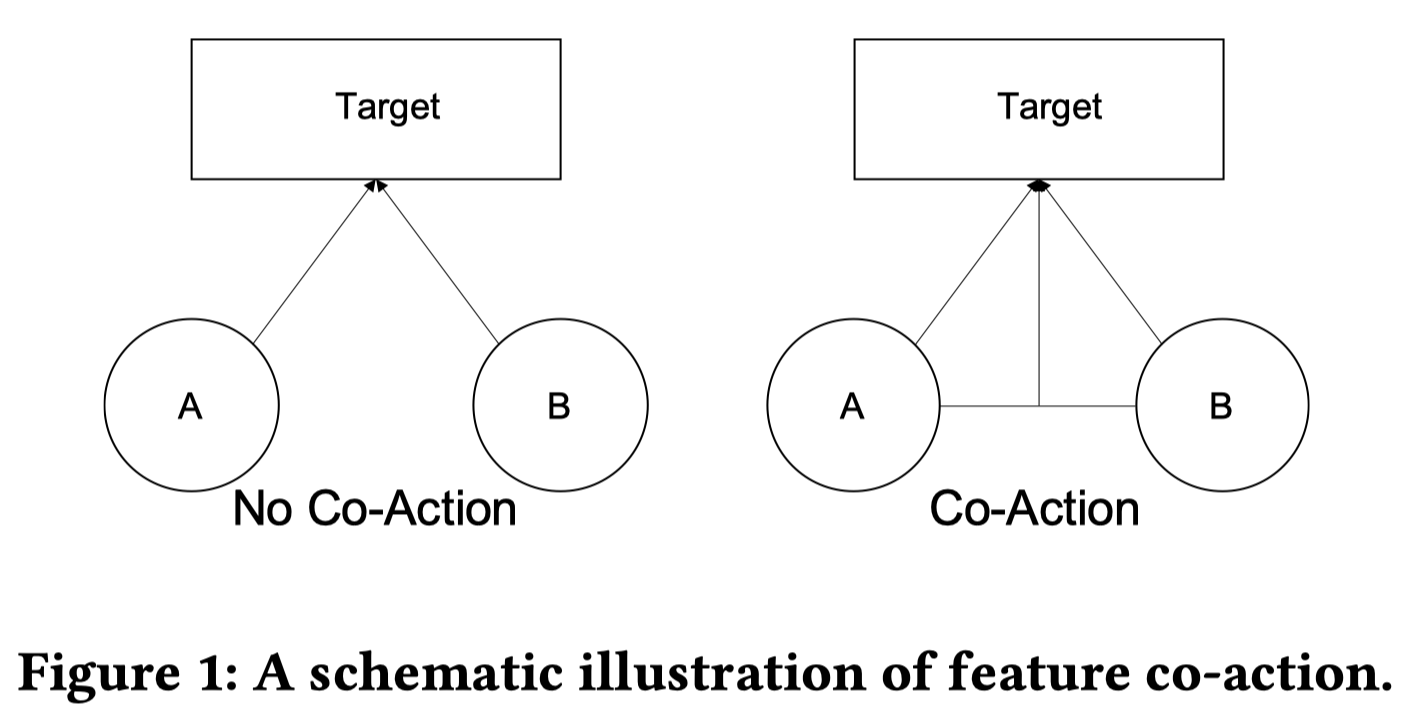
如上图右侧所示，假设只有2种特征A和B用于预测目标。那么特征A和B之间的co-action等价于建模A和B之间的连边，且该连边对于目标的预测也是有影响的，如图中右侧所示：A和B的连边也显式地与目标相连接，这种特征之间的协同效应能够显著影响目标的预测。而没有co-action的系统如图中左侧所示，不同特征之间是独立的，比如通过广义线性模型来预测点击率。

作者认为目前的CTR模型的工作并不能深入地探索到潜在的Co-action特征，并做了相应地实验论证了Co-action被很多模型忽视或低估了。为此，作者提出了一种建模Co-action特征建模网络CAN，即：Co-action Network来挖掘Co-action特征的潜力。CAN能够高效地捕获特征间的Co-action关系，提高模型的性能，并降低计算和存储消耗。实验表明了CAN能够大幅度超越现有的CTR模型。CAN模型已经被部署在阿里巴巴展示广告系统中，获得了12%的CTR提升和8%的RPM提升。

回顾整个研究历程，通过模型来建模co-action效应的方法可以大致分为三大类。

Aggregation based methods，基于汇聚的方法，DIN^[4]，DIEN^[5]，MIMN^[6]等都属于这类方法。基于汇聚的方法主要聚焦于如何从用户历史行为序列中汇聚得到比较有区分性的表征。为了进行有效的汇聚，这类方法通过建模目标item和历史序列item之间的co-action，并作为历史序列行为的权重从而实现加权汇聚。也就是说，co-action在这类方法中仅仅是作为历史行为的权重，并用于信息的汇聚(information aggregation)。
Graph based methods，基于图的方法，GCN^[7]，HINE^[8]等。这类方法将特征作为结点，并相互连接形成图。此时，特征的co-action是作为边的权重来指导信息的传递，即：作为权重系数用于加权汇聚邻域结点的信息。仍然是用于信息的汇聚(information aggregation)。
Combinatorial embedding methods，基于组合嵌入的方法，如FM^[9]，DeepFM^[10]，PNN^[11]等。这类方法通过显式地组合和交叉不同的特征来建模co-action效应。这实际上是一种信息的增强 (information augmentation)，而不是信息的汇聚。例如：PNN在两两特征之间使用内积或者外积来增强输入。但是这种方法的缺点在于，模型要同时负责单一特征的表征学习，又要负责两两特征之间的co-action建模，这二者之间实际上是会有矛盾的，会互相干扰和影响。即：特征co-action是通过单一特征的嵌入来间接表达的，单一特征的学习会影响特征co-action的学习。归根结底，主要是因为特征co-action的学习过程不是独立的。

为了证明如上三种方法在建模co-action方面效果不好，作者和最直接的笛卡尔积方法做比较。所谓的笛卡尔积，即：当特征A和B取值出现共现时，就构造一个新的特征，即A&B，e.g, sex和age特征，某个新特征为：”女性&18岁”，且这个新特征是独立更新的，不会受到诸如”男性&18岁”、”女性&20岁”等特征学习过程的影响。这种方式实际上就是笛卡尔积，也是建模co-action最直接的方式。但是这种方式参数量过大，存在大量低频的稀疏特征。但是作者表明，即便是这样，在实验中，大部分基于组合嵌入的方法都无法打败笛卡尔积方法，可能是因为组合嵌入的方法要同时权衡好单一原始特征的表示学习和多个特征的co-action建模是很困难的。

2. Contributions

为了解决这一问题，作者提出了Co-Action Network(CAN)。这个网络可以在输入阶段就能捕获原始特征的co-action效应，同时能够有效利用不同”co-action特征对”之间通用共享的信息。笛卡尔积的方式的参数量为$O(N^2 \times D)$，$N$为特征量，$D$为向量维度。CAN的参数量为$O(N \times T)$，其中 $T << N$，$D < T$。$CAN$能够将表征学习的嵌入空间和co-action建模的嵌入空间区分开，尽可能减少冲突。具体的，本文的主要贡献点。

阐明了co-action建模的重要性。这种特征co-action效应被大部分现有方法所忽略。通过和笛卡尔积方法做对比也可以观察到这点。
提出了特征Co-action效应建模网络，Co-Action Network(CAN)，这个网络可以在输入阶段就能捕获原始特征的co-action效应。相比于笛卡尔积，能够同时大幅降低模型的参数量。
在公开数据集和真实的工业环境下都做了广泛的实验。目前为止，CAN已经部署在阿里展示广告系统中，CTR提升了12%，RPM提升了8%。
展示了如何部署CAN在真实的工业环境中。CAN所探索的co-action方向以及本文中所提到的一些经验也能够拓展到其它领域中，启发学术界研究者和工业界实践者。

3. Solution

总体上概括下方法。CAN网络和正常的深度CTR网络几乎一样，所不同的是多了个CAN Unit结构。CAN Unit本质上是一种特征提取器，输入是要建模的co-action特征对，输出是建模后的co-action向量。这样，常规的embedding向量和co-action向量拼接起来经过多层MLP，就能输出点击率预估值。CAN Unit的特点是能够将要建模的”特征对”分为weight side和input side。weight side可以reshape成MLP的参数，input side作为MLP的输入，通过多层MLP来建模co-action。

首先回顾下深度CTR预估方法。如果不考虑Co-Action，则预估的label可以表示为：
$$
\hat{y} = \text{DNN}(E(u_1), …, E(u_i), E(m_1), …, E(m_j))
$$
$u$表示user，$m$表示item。$E(\cdot) \in \mathbb{R}^d$表示将稀疏特征映射到嵌入。

如果考虑Co-Action，则预估的label可以表示为：
$$
\hat{y} = \text{DNN}(E(u_1), …, E(u_i), E(m_1), …, E(m_j), {F(u_i, m_j)}_{i,j})
$$
${F(u_i, m_j)}_{i,j} \in \mathbb{R}^d$代表用户特征$u_i$和物品特征$m_j$的交互嵌入表示。构造这种组合特征的直觉来源在于，相比于单一的特征，特征组合可能和label更相关。比如：用户历史点击item和目标预测的item之间的特征组合。

如果$F$是独立的嵌入映射函数，即：和$E$不相关，那么相当于新造了一个特征并独立地映射到某个嵌入表示上，此时这种组合特征是独立地学习的，记忆性最好，对co-action的建模很有效，实际上就是笛卡尔积方法。但是这样的话，组合特征量很大，且大多是低频的，学习过程不稳定。因此不是合理的方法。

如果$F$完全是用$E$来表示的，比如$F(u_i,m_j)=E(u_i) \odot E(m_j)$，$\odot$是element-wise乘积。此时co-action建模不是很有效，因为会受到$E(u_i)$和$E(m_j)$各自单独的学习过程的影响，会导致过度泛化问题。

上述两种方式是两种极端，前者是强记忆性，后者是强泛化性，各有优劣，作者提出的CAN网络希望在二者中做一个折衷，既有记忆性，又有泛化性。

3.1 Co-Action Network

先从总体上介绍下CAN的结构，如下图所示。

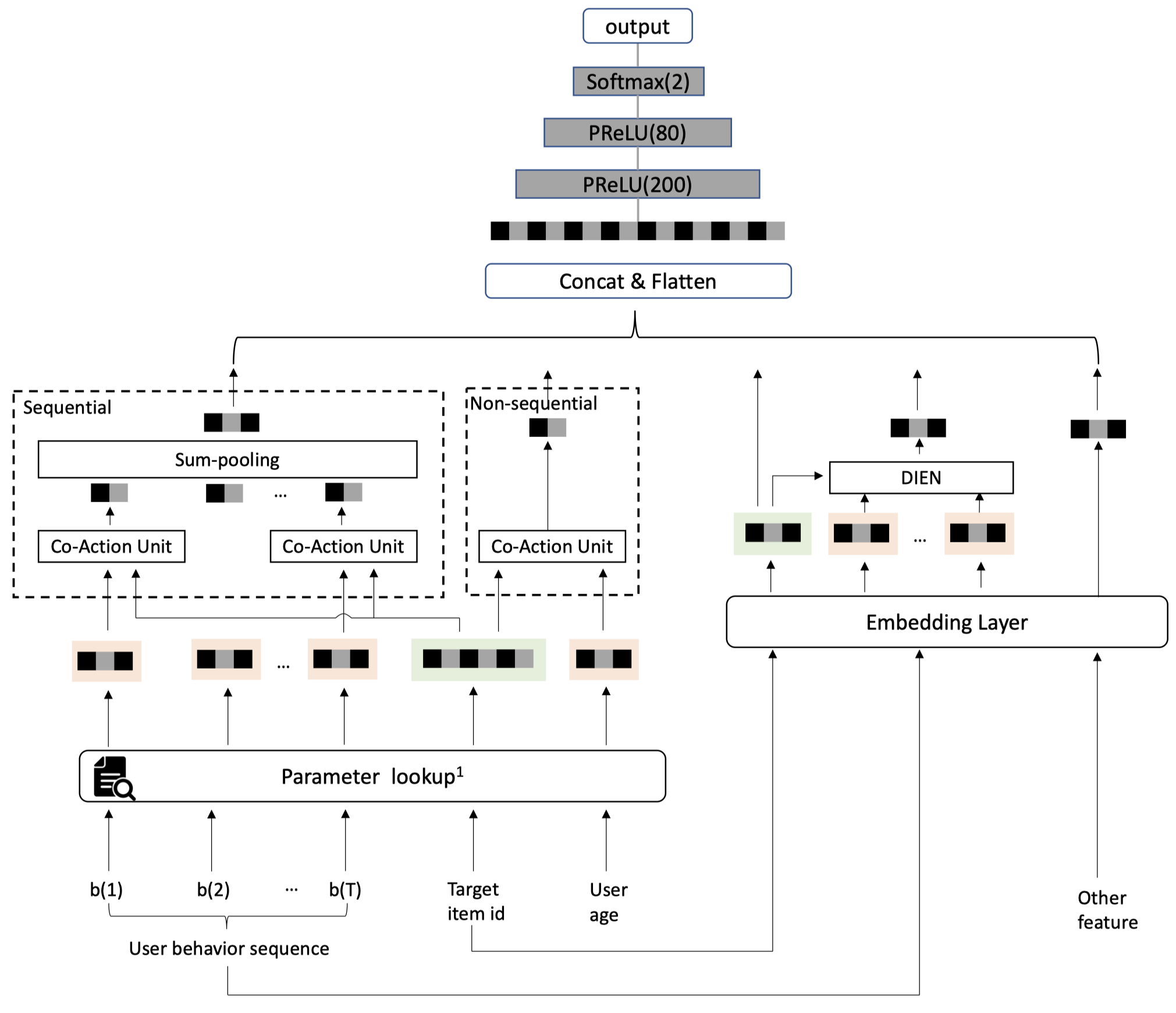
每种特征有两种方式作为CAN的输入。

所有特征经过Embedding Layer：用户侧和物品侧的稀疏特征$x_{user}, x_{item}$都通过emebdding的方式转成稠密向量，用户侧的所有稠密向量concat在一起形成用户向量$e_{user}$，物品侧$e_{item}$同理。即经过图中右侧Embedding layer后输出的向量。可以看到，作者用DIEN来建模user behavior sequence。
部分潜在强co-action效应的特征输入Co-action Unit：从$x_{user}, x_{item}$中选出部分特征作为Co-action Unit的输入来建模强Co-action效应。这部分用户和物品的特征会独立的映射到另一种向量 $p_{user}, p_{item}$上。$p_{user}$和$e_{user}$是独立的两种参数。物品侧同理。即经过图中左侧Paramter lookup后输出的向量。从画出的图可以看出，作者想建模的co-action特征包括两大类：sequence类，如：目标item id和用户历史行为item id；non-sequence类，如：用户年龄age和目标item id。对于序列特征user behavior sequence，每个历史行为item和目标item建模得到的co-action向量经过sum pooling得到最终的序列向量。

则：CAN网络可以形式化为：
$$
\hat{y}=DNN(e_{item}, e_{user}, H(x_{user}, x_{item}, \boldsymbol{\Theta}_{CAN}), \boldsymbol{\Theta}_{DNN})
$$
即：DNN的输入包括了原始特征的嵌入$e_{user}, e_{item}$以及CAN网络输出的co-action嵌入$H$。$\boldsymbol{\Theta}_{CAN}$实际上就是图中Parameter Lookup中的参数。可以看出上述最重要的结构为：Co-action Unit：$H(x_{user}, x_{item}, \boldsymbol{\Theta}_{CAN})$。我们不妨先看下CAN Unit的结构图。

3.2 Co-action Unit

Co-action Unit本质上也是一种特征提取器。输入是要建模的co-action特征对，输出是建模后的co-action向量。

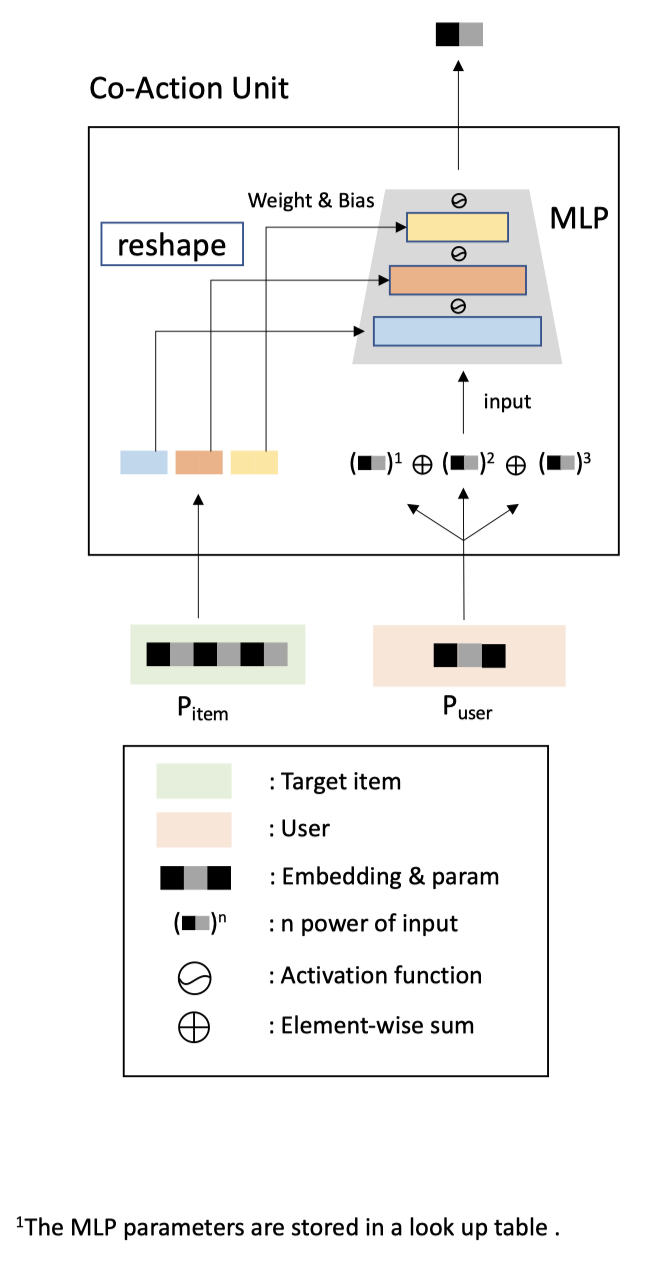
根据上文，想要做到既有记忆性又有泛化性。那么，相比于文章开头所述的第二条迭代路线，即：FM/DeepFM等通过原始单一特征来间接表达co-action的方法，肯定要在此基础上拓展参数空间的大小，并有效地使用这些参数来建模co-action，使得不同特征的学习相对独立，从而提高记忆性。而相比于文章开头所述的第一条迭代路线，即笛卡尔积手动构造组合特征的方法，肯定要在这个基础上一定程度上增加不同的co-action组合特征之间的信息共享，提高泛化性。

为了实现上述目的。作者将要建模co-action效应的两个特征分为了两端。一端拓展了特征的向量维度数，并切分成多个slot向量。不同slot向量可以通过reshape的方式来充当MLP网络不同层参数的角色，另一端则通过手动构造高阶的特征来作为MLP的输入。二者通过多层的MLP来实现co-action效应的建模。

为了符号的清晰，我会用加粗的符号表示矩阵，不加粗的表示向量或者常量。$\boldsymbol{P}_{item} \in \mathbb{R}^{M \times T}$作为MLP每层的权重和偏置参数；$\boldsymbol{P}_{user} \in \mathbb{R}^{N \times D}$作为MLP网络的输入，最终网络输出建模好的co-action向量$H$。

$M$表示item unique ID的数量，$N$是user unique ID的数量(个人认为应该用$N$表示，原文用$M$表示)。$T$是item端拓宽的向量维度数，$D$是user端的向量维度数，$D < T$。当然，user和item可以角色对调。之所以这么做，是因为广告系统中，候选的item数量很少，只占全部item的一小部分，比用户点击历史中的item少的多。（我推测，由于候选item被更多地共享了，所以要拓宽其参数空间，让其学习过程更独立)。

具体而言，MLP第1层每个神经元的连接数和某个user的向量$p_{user} \in \mathbb{R}^D$是一样的，都是$D$维；而$p_{item} \in \mathbb{R}^T$充当着多层MLP参数的容器，即：所有MLP层总共的维度为$T$。为了建模co-action，分为几个步骤：

$p_{item} \in \mathbb{R}^T$通过reshape的方式转成MLP层的权重矩阵和偏置向量参数。即：
$$
P_{item}=\text{concatenate}({\text{flatten}(\boldsymbol{w}^{(i)}), b^{(i)}}_{i=0,…,{K-1}})
$$
$\boldsymbol{w}^{(i)}$是MLP第$i$层的权重矩阵，而$b^{(i)}$是第$i$层的偏置向量。把$\boldsymbol{w}^{(i)}$矩阵拍扁成向量，并和$b^{(i)}$向量拼在一起，这样就形成了第$i$层网络的参数的向量化形式，所有$K$层网络的参数拼接在一起，则形成了所有$K$层网络参数的向量化形式，共T维度。这个过程反向执行，其实就是reshape操作，就能将$T$维向量转成MLP网络的各层参数。比如三层网络，每层参数量一样，即：三层网络的权重矩阵都为$D \times D$维，偏置都为$D$维，则$T=3 \times (D \times D+D)$。
$p_{user} \in \mathbb{R}^D$作为MLP的输入，进行多层MLP前向传播，不同层之间有激活函数。即：
$$
\begin{aligned}
&h^{(0)}=p_{user} \\
&h^{(i)}=\sigma(\boldsymbol{w}^{(i-1)} \otimes h^{(i-1)} + b^{(i-1)}), i=1,2,…,K-1 \\
&H(p_{user}, p_{item}) = h^{(K)}
\end{aligned}
$$
$\otimes$表示矩阵乘法。$H$代表最终输出的feature co-action向量。如果$p_{user}$是用户点击序列中的item，每个历史点击item都会和目标item建模co-action输出1个向量，那么最终的向量表示是这个序列所有item的co-action向量的sum-pooling结果。

那么为何通过这样的网络就能够实现记忆性和泛化性的折衷呢？如何保证Co-Action的建模过程中有相对比较稳定和独立的参数来维持对建模信息的学习记录，同时又想让不同的Co-Action间有一定的信息共享？作者在论文中没有做很直接的解释，下面是个人的一些理解，欢迎纠正。

参数空间的拓展。头部的item出现的次数多，因此通过拓宽其参数空间，并转成MLP的形式；而user作为MLP的输入，这样能够使得两侧特征的参数都能够得到比较好的学习和更新。而在传统的方式中，在提取高阶特征的时候，通常使用共享的MLP，这样不同特征最终的表征向量会受到共享MLP的影响，其梯度又会反向作用MLP的学习，进而又通过共享的MLP影响其他特征的表征向量的学习过程。不同特征之间的梯度信息是耦合在一起的，无法保证稳定且独立的学习。
DNN的计算能力。MLP的主要作用实际上是体现在不同层之间的激活函数，激活函数可以认为充当着门控的角色。reshape操作本质上相当于是对向量空间做了切分，划分为不同的slot，每个slot映射到某层MLP的参数上，且不同slot之间是有信息协同、过滤、递进的关系，通过MLP前向传播矩阵乘法和激活函数来实现的，保证不同slot各司其职，低层的slot负责低level的信息，通过激活函数过滤了噪声后，传到高层的slot来负责高level信息的提取。在梯度反传的时候，不同slot通过激活函数门控机制会接收到不同层次的信息，来保证各自的参数有相对比较独立的更新。进一步，由于激活函数的存在，item A和不同的user特征如B或C做co-action时，B提供给A的梯度信息和C提供给A的梯度信息都会不太一样，保证了参数更新的独立性。

如果不以MLP的视角来看，相当于第一个item slot和user特征做个交互，提取出低阶的信息，激活函数过滤掉无用信息后，再和第二个负责高阶信息提取的item slot做个交互，以此类推。
参数共享。笛卡尔积的话，要学习的co-action特征参数量为$O(N^2 \times D)$。用CAN网络参数量为$O(N \times T)$。而$T$远小于$N$。显然复杂度降低了不少。同时不同co-action之间是有参数共享的。比如，20~25岁 & 化妆品；40~50岁 & 化妆品。物品侧化妆品特征向量是会和多个用户侧年龄特征向量做co-action建模的，因此化妆品会被20~25岁和40~50岁的样本所共享。只不过通过拓宽参数向量为$T$，并通过MLP的门控机制，能够有效地保证这种共享不是过度泛化的，即：$T$维向量不同部分是相对比较独立的。当然，这种共享的程度是否是合适的，很大程度上是受到$T$的大小的影响，$T$太大就过度独立，$T$太小就过度共享。如果有一些参数独立性的措施来保证，可能更有效。后文会提到。

关于user端特征多阶提升的部分，我就不做解读，毕竟这不是文章的关键亮点所在。即：
$$
H(p_{user}, p_{item})=\sum_{c=1}^C MLP_{can}({(p_{user})}^c) \approx MLP_{can} (\sum_{c=1}^C((p_{user})^c)
$$
即：$C$是阶数。$MLP_{can}$是同一个。没有额外的参数量。只在user输入侧对特征做了个多项式变换和相加。

接下来我重点讲一下作者最后一部分提到的多层次独立性multi-level Independence。

参数独立：必须使用。即每个特征都有两种初始的向量，1种是用于表征学习的，即前文提到的$\boldsymbol{e}_{user}$；1种是用于co-action建模的，即前文提到的$p_{user}$。这两个参数是独立的。这一点实际上对我是有启发的。在日常使用DIN的过程中，我发现每个item本身的嵌入和在序列中的嵌入独立开，会比二者共享同一个嵌入的效果更好。可能是因为通过参数独立，可以更好地建模种记忆性的场景。还比如，目标item和序列item直接做笛卡尔积，即：目标item & 序列item1，目标item & 序列item2，依次类推，每一个交叉特征整体都单独作嵌入，这种方式在强记忆性场景也是有效的。
组合独立：推荐使用。前文我们提到，item(参数侧)的特征，会和多种user(输入侧)的特征做co-action建模，这样item是会被共享的，可能会影响学习的独立性。一种思路是，同一个item，对每个不同的user侧特征，用于建模其co-action的item侧特征参数都不一样；user侧同理。这种情况下，如果有N个user特征，M个item特征，那么item侧需要$O(M \times N \times T)$的参数量，user侧需要$O(M \times N \times D)$的参数量。这种方式的参数量和笛卡尔积是相同的，并没有降低参数量。那么其优势只剩下CAN Unit结构本身了。
阶数独立：可选。针对上述user端特征多阶提升做的独立性。即：不同阶对应不同的$MLP_{can}$网络参数。

4. Evaluation

4.1 数据集

Amazon和Taobao建模目标item和用户点击item序列之间的co-action；Avazu建模非序列、离散的特征的co-action。

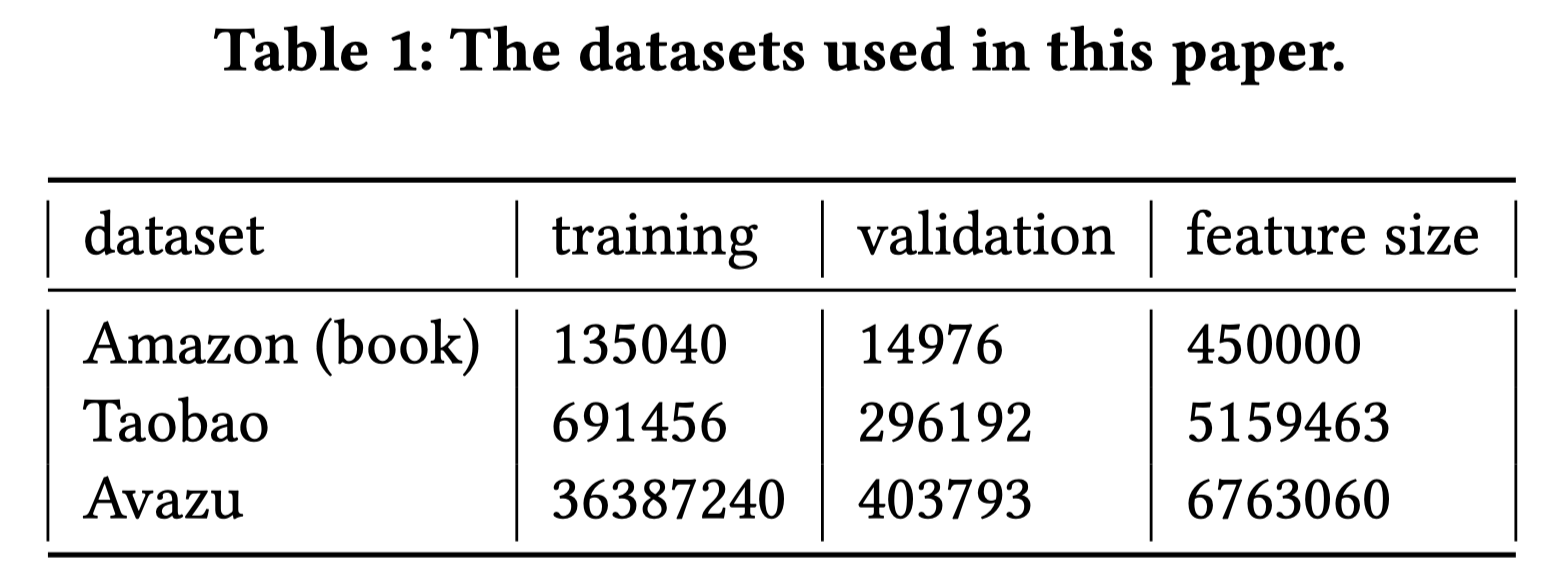
4.2 对比实验

对比模型，DIEN，笛卡尔积，PNN，NCF，DeepFM。
实现细节：$p_{item}$侧，即$MLP_{can}$的参数量：(4x4+4)x8=160维，即8层MLP，每层4个神经元。$p_{user}$的阶数设置为2；参数用零均值标准差为0.01的高斯分布初始化；Adam作为优化器；batchsize为128；学习率0.001；预测层用3层的MLP，尺寸为200x100x2。AUC指标来评估。
模型效果对比：

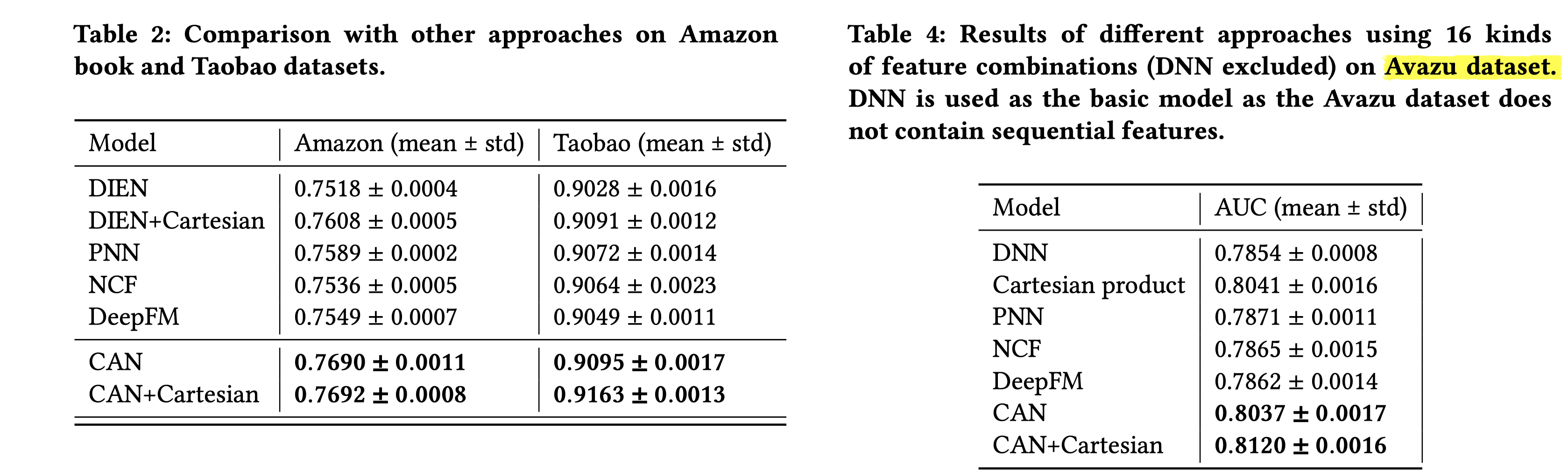
上述几种不同的方法是怎么实现的作者没有具体说明。DIEN，PNN，NCF，DeepFM和原始论文的工作应该是一样的。按照我的理解，这几种方法唯一不同就是co-action特征建模方式。比如对于目标item和点击item序列：DIEN中用attention的方式做加权汇聚；PNN中用内积+外积；NCF用concat+MLP；DeepFM用FM来做。DIEN+Cartesian我认为是先构造目标item和点击item序列的笛卡尔积序列，即：目标item&点击item1，item&点击item2，item&点击item3，..，得到新的序列后，新序列不同项都单独做嵌入，再用DIEN来建模。CAN用CAN-Unit来建模；CAN+Cartesian我个人的理解是multi-level Independence中第二种组合独立中提到的方法。否则，用笛卡尔积构造新序列后，就没必要用CAN来建模了吧。

4.3 消融实验

对比了user侧的阶数，MLP的层数，激活函数不同的差异，看实验结果，这个差异都很小。

4.4 模型通用性和泛化性

通用性：要证明CAN还适用于非序列特征的建模，通过上文表格4中的Avazu数据集上的表现可以看出。
泛化性：将测试集中出现过的组合特征从训练集中去掉。也就是说，训练集中只会出现测试集中的单一特征，而不会出现组合特征。比如：测试集中有”目标item iphone12” & “历史item iphone12 充电器” 这一组合特征，那么训练集中不会出现这种样本，只会出现诸如 “目标item iphone12” & “历史item iphone12 耳机”，或者 “iphone12 耳机” & “历史item iphone12 充电器”。

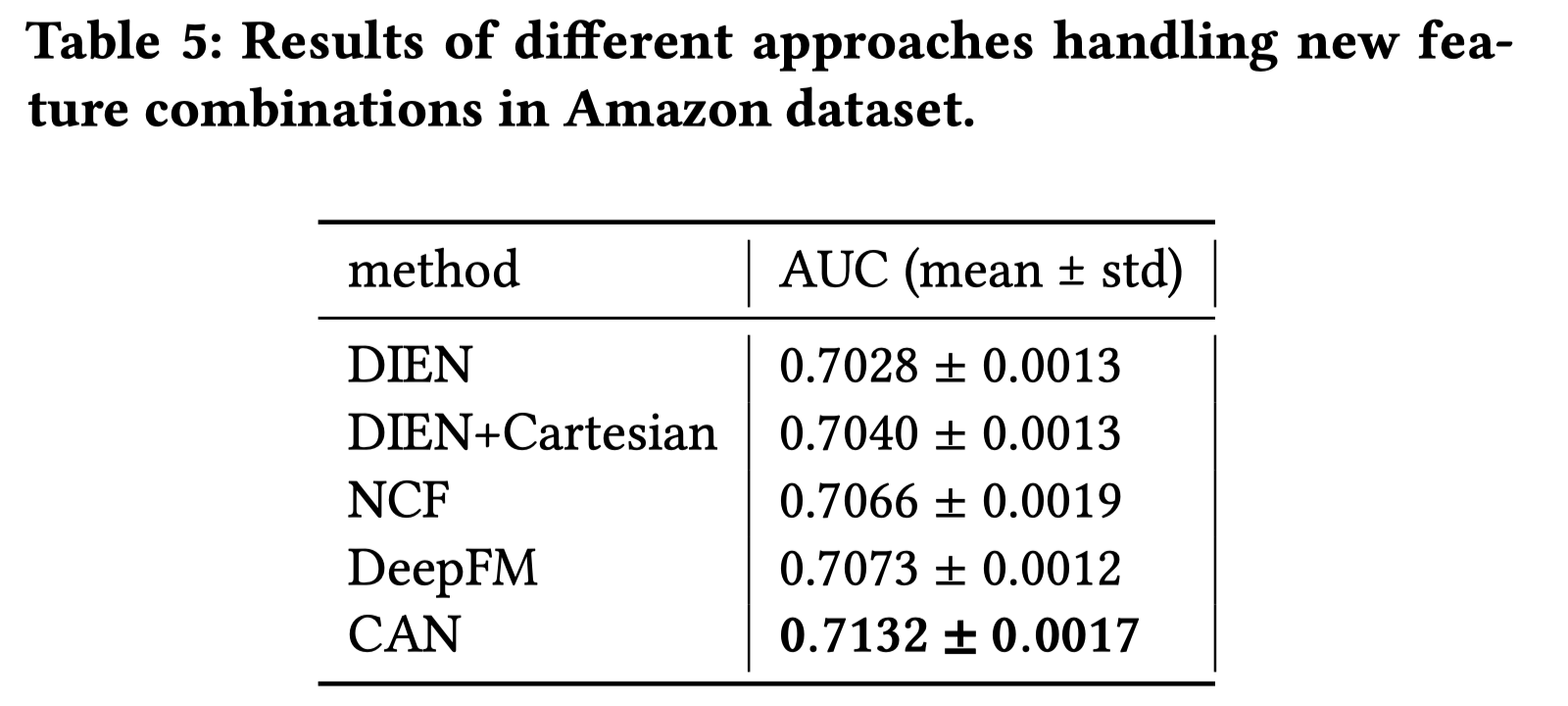
如上图，这种情况下，笛卡尔积还不如NCF，DeepFM等方法，因为笛卡尔积建模的记忆性发挥不了作用，测试集中有很多未看见的特征组合。只要$p_{item}, p_{user}$能够很好地训练，CAN就能表现得很好。我猜测这种情况下，CAN+Cartesian表现得也不好，但是作者没有提到。

4.5 线上部署和实验

最初使用笛卡尔积模型遇到了很多困难。即使做了频率过滤，仍然面临着$M \times N$量级的embedding查表操作。用CAN缓和了很多。CAN最终使用了21种特征来做特征组合，包括6种广告特征，15种用户特征。因此，根据参数独立性，有21种额外的参数空间被分配用于建模co-action。这种仍然无法忍受，因为用户特征很多是长序列特征，超过100，内容访问延迟增加了不少。解决思路：

序列长度裁剪。减少到50。QPS提高了20%，AUC降低了0.1%，可接受。
特征组合约减。6个广告特征+15种用户特征可以组合出90个新特征。但是不是所有的组合都是必要的。作者只针对相同类型的广告和用户特征做组合，比如item id和用户item id序列；item category id和用户item category id序列。组合特征从90降低到48，提高了30%的QPS。
计算内核优化。co-action主要耗时在于大矩阵乘法。item侧和user侧序列的计算参数量形式化为，[Batch_size × K × dim_in × dim_out] × [batch_size × K × seq_len × dim_in]。主要是因为dim_out和dim_in的不是常用的形状，导致BLAS库不能很好地优化计算，因此可以对底层进行重写。提高了60%的QPS。进一步，序列每个item进行co-action建模后，需要做sum-pooling，作者把这个sum pooling过程和矩阵乘法融合在一块了，好处是可以避免写矩阵乘法的结果到GPU中，这个又提高了47%的QPS。

最终，CAN的CTR预估的时间耗时是12ms，每块GPU可以处理1K的QPS。在两种场景下（没有说是什么场景）的提升如下表。

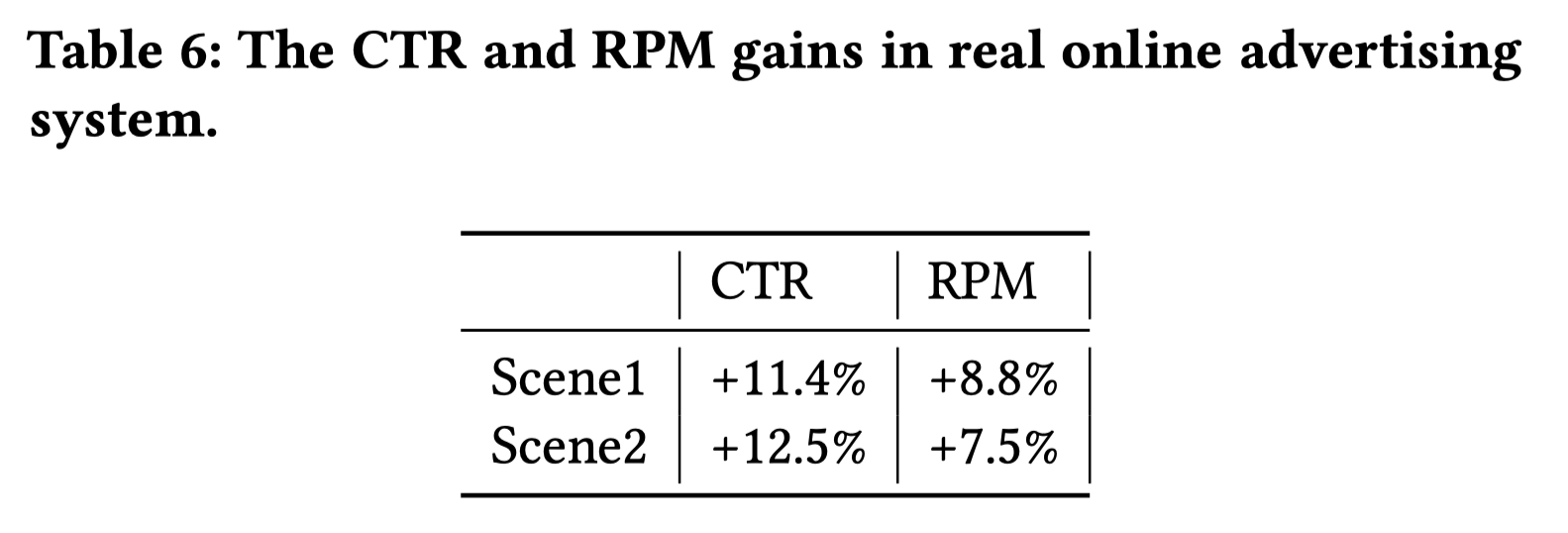
5. Summarization

本文作者提出了一种特征交互的新思路，在记忆性和泛化性之间做了折中。CAN网络能够将表征学习和Co-action建模二者区分开，并通过多层次的独立性等技巧来提升模型的表达能力。

总之，不管是DIN/DIEN还是CAN，其目的都是为了增强co-action特征的表达能力。DIN这类方法比较soft，而笛卡尔积又过于hard。CAN在二者之间做了个折中，通过网络参数化的方式能够增强co-action特征的表达能力，同时由于拓宽了co-action的参数空间、co-action的参数空间和表征学习的嵌入空间之间的独立性、激活函数门控机制等，就能够保证co-action参数不同的部分有相对比较稳定和独立的参数来维持对建模信息的学习记录，同时又能让不同的co-action间有一定的信息共享。

现在的研究工作通常将特征工程的工作转移到模型层面来做，更fancy，更简便，通用性更强。但是也值得强调的是，模型层面的很多工作可以由特征工程替代，且在实际场景中可能更快拿到收益。比如将用户的行为按时间周期做划分并分别统计，可以刻画周期时间与用户兴趣的关系；比如将目标Item特征和用户历史行为Item特征做手动交叉，可以直接刻画用户行为与Item的联系，将DIN或者DIEN想要达成的目标转化为手工特征作为信息输入是可行的。CAN这个工作虽然也是模型层面建模特征的工作，但是其核心思想融入了很多手工特征的思路，个人认为是一个很有启发性的工作。

References

[1] CAN: Revisiting Feature Co-Action for Click-Through Rate Prediction：https://arxiv.org/abs/2011.05625

[2] 想为特征交互走一条新的路： https://zhuanlan.zhihu.com/p/287898562

[3] 推荐系统之Co-action Network理解与实践：https://mp.weixin.qq.com/s/45fYiM2FK3ZwigIUrmCnmg

[4] DIN，KDD2018，Deep Interest Network for Click-Through Rate Prediction：https://arxiv.org/abs/1706.06978

[5] DIEN，AAAI2019，Deep Interest Evolution Network for Click-Through Rate Prediction：https://arxiv.org/abs/1809.03672

[6] MIMN，KDD2019，Practice on Long Sequential User Behavior Modeling for Click-through Rate Prediction：https://arxiv.org/abs/1905.09248

[7] GCN，ICLR 2017，Semi-Supervised Classification with Graph Convolutional Networks：https://arxiv.org/abs/1609.02907

[8] HINE，TKDE 2019 Heterogeneous Information Network Embedding for Recommendation：https://arxiv.org/pdf/1711.10730.pdf

[9] FM，ICDM 2010，Factorization machines：https://ieeexplore.ieee.org/document/5694074

[10] DeepFM，IJCAI 2017，DeepFM: a Factorization-Machine based Neural Network for CTR prediction：http://www.ijcai.org/Proceedings/2017/0239.pdf

[11] PNN，ICDM 2016，Product-based neural networks for user response prediction：https://arxiv.org/abs/1611.00144

最后，欢迎大家关注我的微信公众号，蘑菇先生学习记。会定期推送关于算法的前沿进展和学习实践感悟。