本文对Ng提到的关于机器学习应用实践上的建议进行整理总结。主要内容包括:诊断(Diagnostics for debugging learning algorithms)、误差分析(error enalysis)、销蚀分析(ablative analysis)、过早优化(premature optimization)。并结合“自动驾驶直升机”应用探讨如何对存在问题进行诊断。
ML算法诊断
考虑前面”生成算法”一文中讨论的垃圾邮件分类问题。前面我们使用50000+词语的词典作为特征向量集,本文将从中挑选100个词作为特征集。并使用”Learning Theory(2)”中提到的贝叶斯逻辑回归进行分类。代价函数如下,多了正则化项:
$$\max_{\theta} \sum_{i=1}^m log p(y^{(i)}|x^{(i)},\theta)-\lambda ||\theta||^2$$
使用梯度上升方法来进行极大似然估计,注意因为我们要最大化上述式子,故正则化项前为减号。(之前我们的目标是最小化,因为之前第一项对数似然取负号,故要加上正则化项,这里相当于对之前整个式子取负号,将最小化转成最大化,相应的变为减正则化项)。
目前研究状况是测试误差达到了20%, 这个结果显然不能接受,我们下一步要怎么做呢?
可能的方法包括:
- 尝试获取更多的训练数据(Try getting more training examples)
- 尝试减少特征(Try a smaller set of features)
- 尝试增加特征(Try a larger set of features)
- 尝试选择更好特征(Try changing the features)
- 尝试对梯度下降方法多迭代几次(Run gradient descent for more iterations)
- 尝试使用牛顿法,牛顿法收敛更快(Try Newton’s method)
- 修改正则化系数\(\lambda\)(Use a different value for \(\lambda\))
- 尝试其他算法,如SVM算法(Try using an SVM)
可能的方法数以百计,我们只列出这么多。对于上述8种改进方法,如果一一尝试的话非常耗时。比如第一条,增加数据一般会达到比较好的效果,但对于一些应用来说,收集数据是很困难耗时的事情,如果你花了三个月的时间来收集数据,但最后发现增加数据并没有使算法效果编号,那就悲催了!
更好的解决方法是,使用诊断法来发现问题所在。偏差/方差分析
第一个方法是判断问题是出在高方差还是高偏差。一般来说,高方差反映了过拟合问题,即训练误差很小但泛化误差却很大。而高偏差反映了模型本身存在问题或特征太少等问题,此时训练误差和泛化误差都很大。高方差诊断
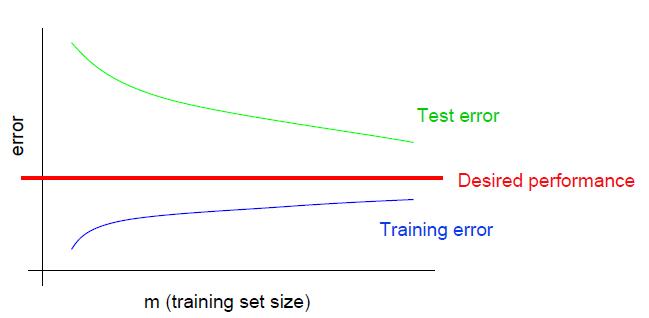
上图是高方差情况下,训练误差和泛化误差随样本数量变化的情况。该图有几个重要特征: - 泛化误差随样本m增大而降低。
Test error still decreasing as m increases,并且不断逼近期望误差,意味着增加数据可以起到作用。 - 训练误差和泛化误差之间差距很大。
Large gap between training and test error,训练误差一直比期望误差理想,意味着可能存在过拟合。
高偏差诊断
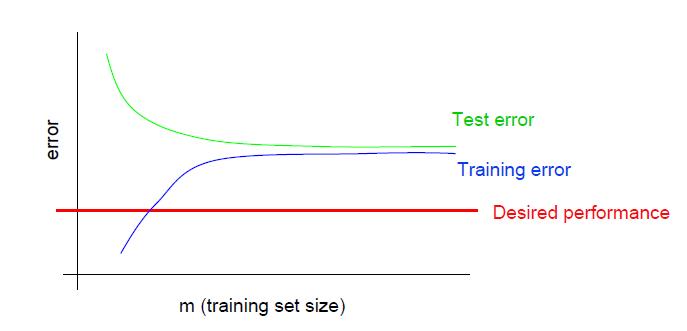
上图是高偏差的情况下,训练误差和泛化误差随样本数量变化的情况。该图有几个重要特征:
- 训练误差很大。
Even training error is unacceptably high, 比期望的误差还大。 - 训练误差和泛化误差之间差距很小。
Small gap between training and test error.
二者最明显的区别就在于,训练误差和泛化误差间的差距大小以及训练误差和理想误差的差距大小。
前者体现在,\(m\)较大的时候,高方差对应的训练误差和泛化误差的差距较大,高偏差对应的训练误差和泛化误差的差距较小。
后者体现在,在\(m\)较小的时候,高方差的训练误差比理想误差还小,或者说维持在一个较优的水平;而高偏差的训练误差一般比理想误差大,维持在一个较差的水平。
上述图片也称作学习曲线。根据上面的分析,我们可以对前面提到的8条解决思路前4条进行分类。
- 尝试获取更多的训练数据。———— 解决高方差
- 尝试减少特征。————解决高方差
- 尝试增加特征。————解决高偏差
- 尝试选择更好特征。———— 解决高偏差
收敛与目标函数分析
考虑下面的情景,仍然是针对垃圾邮件分类问题:
- 使用贝叶斯逻辑回归(BLR)可以达到垃圾邮件上的2%错误率,正常邮件上2%的错误率。
正常邮件上的如此高的错误率是无法接受的。 - 使用SVM模型可以达到垃圾邮件10%的错误率,正常邮件0.01%的错误率。
可以接受。 - 显然这个场景下SVM表现更好。但是因为计算效率上的考虑,你想使用逻辑回归,该如何解决?
对于这种情况,有如下两种分析。 - 算法是否收敛?(Is the algorithm(gradient descent for BLR) converging?)
算法收敛程度和训练优化算法以及迭代次数关系很大。训练优化算法包括梯度下降、牛顿法、SMO等 - 目标优化函数是否合适?(Are you optimizing the right function?)
目标函数是否正确包括目标函数里的参数设置,例如BLR中正则化项系数\(\lambda\),SVM对偶问题中的惩罚因子\(C\)。另外,不同模型使用的目标函数不同,例如SVM使用对偶问题目标函数,因此目标函数还和模型相关。
这两种情况都有可能造成上面的SVM优于BLR的问题。如果BLR没有收敛,SVM比BLR收敛的更好,所以SVM效果更好。如果模型的目标函数没有找对,也可能造成上述问题。
对于函数是否收敛来说,我们可以画出迭代次数与目标函数值的趋势图,但是这样的趋势图在通常情况下很难分辨出目标函数是否稳定的趋势,因为在训练的后期目标函数的每步优化往往都只提高一点。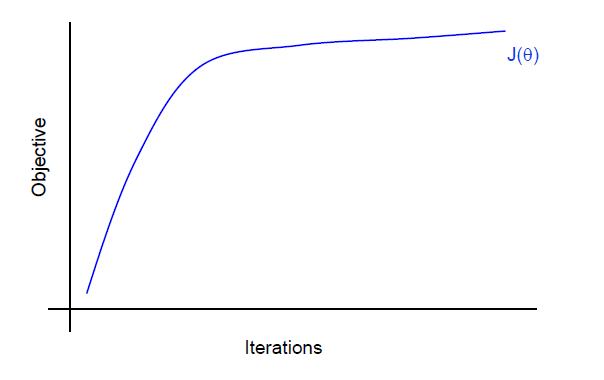
上图很难看出是否收敛,目标函数似乎还在增长.(注意本文使用的是最大化目标函数)
这里介绍一种更直观的方法。
首先我们关注的是分类的准确率,并且对于正常邮件应当给予更高的权重。
$$a(\theta)=\max_{\theta} \sum_{i} w^{(i)} I\{h_\theta(x^{(i)})=y^{(i)}\}$$
\(w^{(i)}\)代表权重,在正常邮件中权值更大。
我们令\(\theta_{SVM}\)为SVM模型学习到的参数结果,\(\theta_{BLR}\)为Bayesian logistic regression学习到的参数结果。
显然根据我们前面的假设,SVM效果比BLR好,则:
$$a((\theta_{SVM}) > a(\theta_{BLR})$$
再来观察目标函数值对比。
BLR尝试最大化如下目标函数:
$$J(\theta) = \sum_{i=1}^m log p(y^{(i)}|x^{(i)},\theta)-\lambda ||\theta||^2$$
SVM尝试最小化如下的原始目标函数为:
$$\min_{w,b} \frac{1}{2}||w||^2 + C\sum_{i=1}^m \zeta \\\\
使得, y^{(i)} (w^T x^{(i)}-b) \geq 1- \zeta
$$
转成对偶问题后,变成最大化对偶问题目标函数:
$$\max_{\alpha} W(\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j <x^{(i)},x^{(j)}> \\\ 使得, \alpha_i \geq 0, i=1,…,m \\\ \sum_{i=1}^m \alpha_i y^{(i)} = 0$$
我们将比较\(J(\theta_{SVM})和J(\theta_{BLR})\)
- 情况1
$$a(\theta_{SVM}) > a(\theta_{BLR})且J(\theta_{SVM})>J(\theta_{BLR})$$
我们注意到,BLR尝试最大化目标函数,SVM尝试最大化对偶目标函数。\(J(\theta_{SVM})>J(\theta_{BLR})\)表明SVM收敛得比BLR好。因此问题可能出在优化算法,应该改进训练优化算法,例如使用牛顿法替换梯度下降,使之收敛更快。 - 情况2
$$a(\theta_{SVM}) > a(\theta_{BLR})且J(\theta_{SVM}) \leq J(\theta_{BLR})$$
这种情况表明,BLR收敛没问题,SVM收敛性能比BLR更差,结果却更优。意味着目标函数\(J(\theta)\)存在问题,其不能真实反应人们在该问题上的需要(后面无人机诊断实例就能明白),应该改进目标函数。要么进行调参,要么考虑换模型,也就间接地更改了目标函数。
因此,我们可以对解决思路后四条进行分类。
- 尝试对梯度下降方法多迭代几次。————解决优化算法(optimization algorithm)
- 尝试使用牛顿法。———— 解决优化算法(optimization algorithm)
- 修改目标函数参数(\(\lambda,C\)等)。————解决目标函数(optimization objective)
- 尝试其他算法(SVM算法),相当于修改目标函数。————解决目标函数(optimization objective)
诊断实例
Ng和他的一些学生正在做一个自动驾驶直升机飞行的项目。本文以此为例子来分析Ng之前在遇到问题时是如何入手解决的。
首先对于一个能够自动驾驶直升机的程序来说,要经过如下步骤:
- 建立一个精确的模拟器(Build a simulator of helicopter)
- 选择一个代价函数。(Choose a cost function)
$$eg: J(\theta)=||x-x_{desired}||^2$$ - 使用强化学习算法在模拟器中飞行来对代价函数进行最小化优化。(Run reinforcement learning algorithm to fly helicoper in simulation)
$$得到输出参数:\theta_{RL}= arg \min_{\theta}{J(\theta)}$$
假设已经做了如上步骤。但是得到的控制参数\(\theta_{RL}\)驾驶的实际效果比真人驾驶的效果差很多。此时该如何入手解决呢?
可能的措施包括: - 提升模拟器性能。(使其更符合真实环境)
- 修改代价函数J(使最优化代价函数能够反映出飞行表现良好)
- 修改RL算法(优化算法,使代价函数更好得收敛)
我们假设在理想情况下,即上述步骤都很完美得完成了。 - 直升机模拟器是精确的。(能够很好模拟真实环境)
- 最小化代价函数意味着能够正确的自动驾驶。(该代价函数能够反映实际需求:完美飞行)
- RL算法在模拟器环境下正确得最小化了代价函数。(算法没问题:能求解问题)
如果上述条件都满足,那么毫无疑问,直升机会在实际环境中飞行得很好。
我们使用如下的诊断方法: - 如果算法求出的控制参数\(\theta_{RL}\)在模拟器中飞行得很好,但是在实际环境中却表现很差。问题很可能出在模拟器上。比如,模拟器无法真实模拟出现实环境的气压、风向等因素。
- 让真实的人来驾驶直升飞机,得到参数\(\theta_{human}\),如果\(J(\theta_{RL})>J(\theta_{human})\),即人操作得到的代价函数更小,也就说明算法收敛不够,那么需要考虑改进优化算法,使算法更加收敛,可以考虑修改强化模型的优化算法或改成其他模型。
- 如果\(J(\theta_{RL})<J(\theta_{human})\),则问题出在代价函数的设计上,代价函数已经很好得收敛了,结果却不好。即该代价函数最小化并不能代表飞行好。(Minimizing it doesn’t correspond to good autonomous flight)此时需要对代价函数重新设计。
因此我们需要为算法设计诊断方法来发现问题所在。即使你的算法表现良好,你也可以运用诊断方法来更加深入理解整个运行机制。这有助于理解问题的本质,有助于得到一个直观的感觉,什么样的改进能起作用,什么样的改进不起作用。同时运行诊断方法以及后面谈到的误差分析方法能够更好得对问题和观点进行阐述,从而写出更具有研究性的论文。误差分析
误差分析用来判读误差的来源。
实际过程中,一个系统可能由多个部件组成,比如一个基于人脸的性别识别系统,可能由如下几个部件组成,按流程处理的先后顺序如下: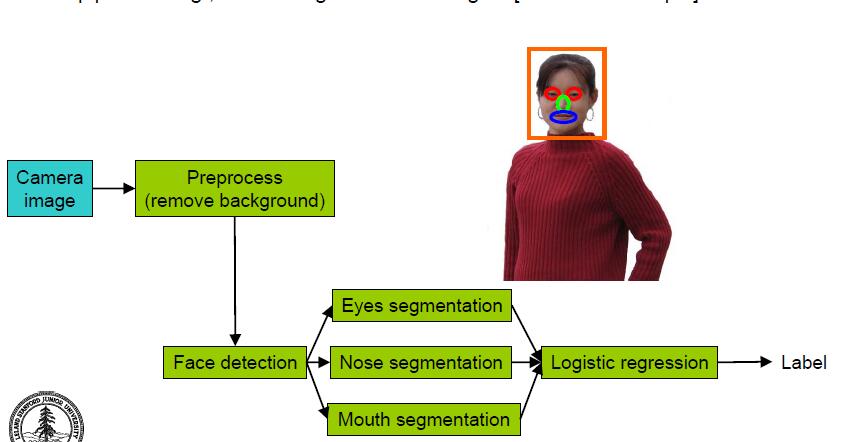
所谓的误差分析,做法就是对每个部件用基准值代替算法的输出,然后观察最后结果的变化,可能的误差分析结果如下: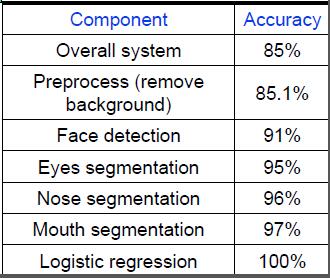
如上图,系统整体的性能是85%准确率。我们使用一个已经对背景进行消除的照片进行建模(相当于拍了一张不带背景的照片,即不需要我们模型进行预处理),此时得到的准确率是85.1%,显然只有0.1%的提升; 我们再在此基础上进行处理,固定其他因素不变,直接将人脸所在位置告诉模型(不需要模型进行人脸位置的检测),然后进行建模(注意此时是在第一步的基础上的,即用不带背景的照片进行人脸检测),发现性能为91%,相较于85.1%提升了5.9%。同理对于器官检测,我们可以告诉模型眼睛所在位置,得到95%的准确率,提升4%等等。如果最终将所有的处理都用基准值代替,即所有的步骤人工告知模型,那么最后Logistic得到的结果是100%.
经过这样的分析,我们可以得出,对于较多的部分是人脸识别和眼睛识别。当然,器官识别中不同的基准值代替顺序可能会有不同的分析结果,所以可以调整顺序不断进行比较,找到问题的瓶颈所在。销蚀分析
销蚀分析与误差分析不同,误差分析师一步步用基准值代替算法输出,比较的是系统当前性能与最高性能的差别。而销蚀分析考虑的是系统性能和底线性能(baseline)的差异。
比如,对于拉简邮件分类器来说,先构建一个初始分类器,然后考虑一些比较高级的特征,比如邮件的语法风格,主机信息,标题等。先将所有特征全部加入分类器,然后逐个剔除,观察性能的下降幅度,将那些性能下降少或者反而导致性能提升的特征去除。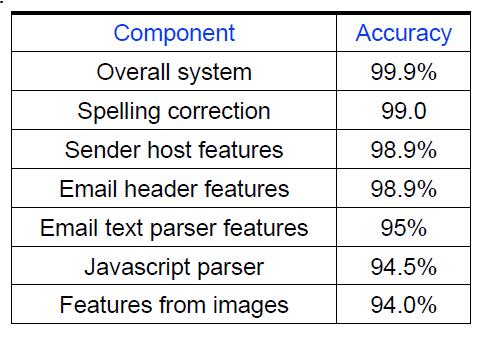
如上图,显然Email text parser features最重要。
如何开始ML问题的解决
途径1:精心设计法(Careful design)
对问题进行深入分析,提取正确的特征,收集正确的数据,设计正确的算法架构,最终实现它。好处在于能一次性能到可扩展的算法,甚至可能会创造一些新的算法。有点类似瀑布流开发模式。
途径2:构建修改法(Build-and-fix)
使用一些粗糙但是快速的方法进行初步构建。然后使用诊断法和误差分析法来分析问题所在,并修正误差。好处在于可以较快的构建应用,快速占领市场。因为互联网上的成功产品,很多往往不是做的最好的,而是最早占领市场的。
过早优化(Premature statistical optimiztion)
通常情况下,是很难发现系统哪个部分是比较容易或者比较难构建的,也很难发现系统哪部分需要花更多时间进行开发。也因此上述途径1的精心设计方法很容易陷入过早优化问题,即对系统的某个部分过早的进行精心设计,却不知这部分设计是否是真的对系统性能有很大影响。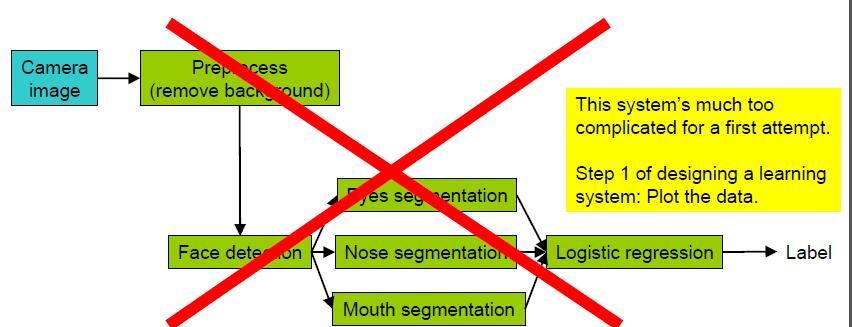
The only way to find out what needs work is to implement something quickly,and find out what parts break。即通过快速入手一些工作来发现哪部分是需要多花时间,哪部分不需要多花时间。一个较好的建议是先对数据进行分析,比如为什么数据中这些属性是负的,当找出数据中的规律或者数据中的错误时,往往会发现系统性能差不是需要更复杂的算法,而是更强大的预处理。
过度理论(over-theorizing)
在做研究时,要把注意力集中在关键问题上,不要轻易的相信某些理论对算法有用而花大量的时间在那些理论上。比如如果要检测出图片中的物体,可能有人会说三维微分几何对这个问题有用,但是在你确认这个确实有用前,不要浪费精力在这个上面。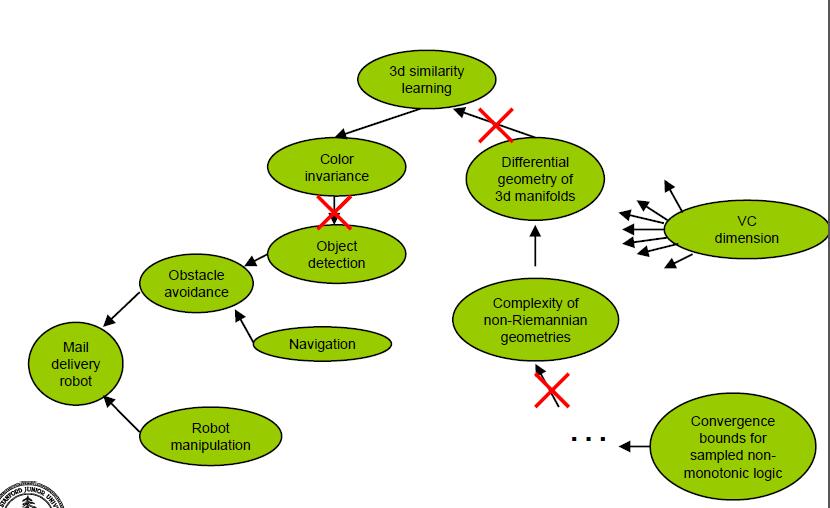
总结
- 花在设计诊断方法上的时间是值得的。
- 需要根据自己的直接和经验来来设计正确的诊断方法
- 误差分析和销蚀分析用于可以提供对问题的深入理解
- 两种途径入手机器学习问题:精心设计法(容易陷入过早优化)、构建修改法。

