本文主要介绍因子分析模型(Factor Analysis Model)。因子分析模型是对高斯混合模型存在的问题进行解决的一种途径。同时也是属于“空间映射”思想的一种算法。本文将对因子分析模型进行介绍,并使用EM算法进行求解。
引入
在上一篇笔记中混合高斯模型,对于混合高斯模型来说,当训练数据样本数据小于样本的维度时,因为协方差矩阵是奇异的,导致不能得到高斯概率密度函数的问题。(\(\Sigma\)出现在分母)
追本溯源,这个问题可以认为数据信息缺乏的问题,即从训练数据中得不到模型所需要的全部信息。解决方法就是减少模型所需要的信息。本文提到的手段有两个,第一个就是不改变现有模型,但是加强模型的假设,例如可以对协方差矩阵进行限制,使协方差矩阵为对角矩阵,或者进一步假设对角矩阵上的对角线数值都相等,此时只要样本大于1就可以估计出限定的协方差矩阵。第二个手段则是降低模型的复杂度,提出一个需要更少参数的模型,因子分析模型就属于此类方法。本文重点讨论该模型。
边缘和条件高斯分布
在讨论因子分析之前,先看看多元高斯分布中,条件和边缘高斯分布的求法,这个在后面因子分析的EM推导中有用。
假设x是有两个随机向量组成(可以看作将之前的\(x^{(i)}\)分成了两部分)
$$x=\begin{bmatrix}x_1 \\\ x_2 \end{bmatrix}$$
其中,\(x_1 \in \mathbb{R}^r, x_2 \in \mathbb{R}^s, 则x \in \mathbb{R}^{r+s}\)。假设x服从多元高斯分布\(x \sim N(\mu,\Sigma)\),其中:
$$\mu = \begin{bmatrix}\mu_1 \\\ \mu_2 \end{bmatrix}$$
$$\Sigma=\begin{bmatrix}\Sigma_{11} \ \Sigma_{12} \\\ \Sigma_{21} \ \Sigma_{22} \end{bmatrix}$$
其中,\(\mu_1 \in \mathbb{R}^r,\mu_2 \in \mathbb{R}^s,则\Sigma_{11} \in \mathbb{R}^{r*r},\Sigma_{12} \in \mathbb{R}^{r*s}\),由于协方差矩阵是对称的,故\(\Sigma_{12}=\Sigma_{21}^T \)。整体上看,\(x_1,x_2\)联合分布符合多元高斯分布。
那么只知道联合分布的情况下,如何求\(x_1\)的边缘分布呢?从上面\(\mu,\Sigma\)可以得出:
$$E[x_1]=\mu_1, \ Cov(x_1)=E[(x_1-\mu_1)(x_1-\mu_1)^T]=\Sigma_{11}$$
下面我们验证第二个结果:
$$Cov(x)=\Sigma \\\\
=\begin{bmatrix}\Sigma_{11} \ \Sigma_{12} \\\ \Sigma_{21} \ \Sigma_{22} \end{bmatrix} \\\\
=E[(x-\mu)(x-\mu)^T] \\\\
=E\left[\begin{bmatrix}x_1-\mu_1 \\\ x_2-\mu_2 \end{bmatrix} {\begin{bmatrix}x_1-\mu_1 \\\ x_2-\mu_2 \end{bmatrix}}^T \right] \\\\
=E \begin{bmatrix} (x_1-\mu_1)(x_1-\mu_1)^T \ (x_1-\mu_1)(x_2-\mu_2)^T \\\ (x_2-\mu_2)(x_1-\mu_1)^T \ (x_2-\mu_2)(x_2-\mu_2)^T \end{bmatrix}
$$
由此可见,多元高斯分布的边缘分布仍然是多元高斯分布。也就是说:
$$x_1 \sim N(\mu_1, \Sigma_{11})$$
上面求得是边缘分布,让我们考虑一下条件分布的问题,也就是\(x_1|x_2\)。根据多元高斯分布的定义:
$$x_1|x_2 \sim N(\mu_{1|2},\Sigma_{1|2})$$
且:
$$\mu_{1|2}=\mu_1 + \Sigma_{12} \Sigma_{22}^{-1}(x_2-\mu_2)$$
$$\Sigma_{1|2}=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1} \Sigma_{21}$$
这是接下来计算时需要的公式,这两个公式直接给出。
因子分析模型
形式化定义
在因子分析模型中,我们假设有如下关于(x,z)的联合分布,其中z是隐含随机变量,且\( z \in \mathbb{R}^k\)
$$z \sim N(0,I)$$
$$x|z \sim N(\mu+\Lambda z,\Psi)$$
其中,模型的参数是向量\(\mu \in \mathbb{R}^n\),矩阵\(\Lambda \in \mathbb{R}^{n*k}\)以及对角矩阵\(\Psi \in \mathbb{R}^{n*n}\)。\(k\)的值通常取小于\(n\)。
因子分析模型数据产生过程的假设如下:
- 1) 首先,在一个低维空间内用均值为0,协方差为单位矩阵的多元高斯分布生成m个隐含变量\(z^{(i)}\),\(z^{(i)}\)是k维向量,m是样本数目。
- 2) 然后使用变换矩阵\(\Lambda\)将z映射到n维空间\(\Lambda z\)。此时因为z的均值为0,映射后的均值仍然为0。
- 3) 再然后将n维向量\(\Lambda z\)再加上一个均值\(\mu\),对应的意义就是将变换后的z的均值在n维空间上平移。
- 4)由于真实样例x会有误差,在上述变换的基础上再加上误差\(\epsilon \in N(0,\Psi)\)
- 5) 最后的结果是认为训练样例生成公式为\(x=\mu+\Lambda z + \epsilon\)
因此,我们也可以等价地定义因子分析模型如下:
$$z \sim N(0,I) \\\ \epsilon \sim N(0,\Psi) \\\ x=\mu+\Lambda z + \epsilon$$
其中,\(\epsilon和z\)是独立的。
示例
让我们看一个样本生成的例子方便理解因子分析模型。假设:\(z \in \mathbb{R}^1, x \in \mathbb{R}^2\)。z是一维向量,x为二维向量,再假设\(\Lambda=[1 \ 2]^T, \Psi=\begin{bmatrix} 1 \ 0 \\\ 0 \ 2 \end{bmatrix} \mu=[3 \ 1]^T\)
假设我们有m=5个二维样本点\(x^{(i)}\),两个特征如下: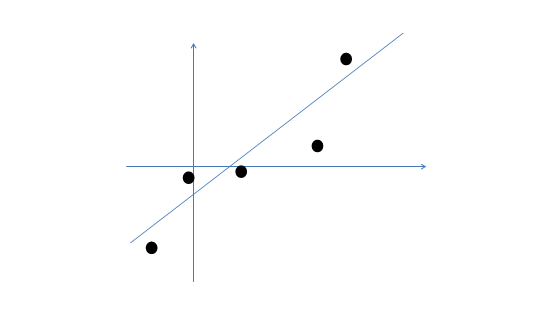
按照生成过程的5步。
1.第一步,我们首先认为在一维空间(这里k=1),存在着按高斯分布\(N(0,I)\)生成m个隐含变量\(z^{(i)}\)。如下: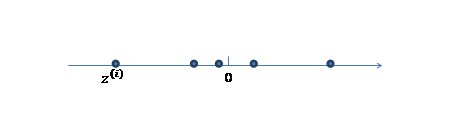
2. 然后使用某个\(\Lambda\)将一维的z映射到二维,图下: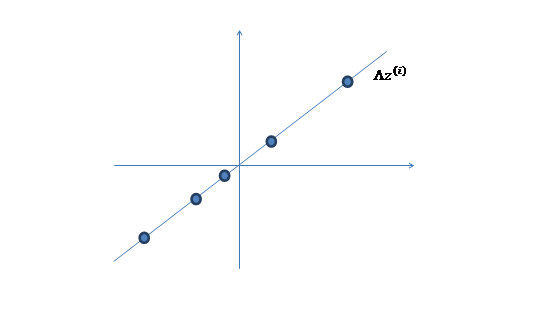
3. 之后加上\(\mu(\mu_1,\mu_2)^T\),即将所有点的横坐标移动\(\mu_1\),纵坐标移动\(\mu_2\),将直线移到一个位置,使得直线过点\(\mu\),原始左边轴的原点现在为\(\mu\)(红色点)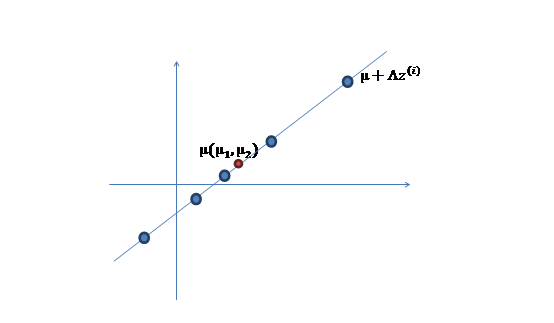
4. 然而,样本点不可能这么规则,在模型上会有一定偏差,因此我们需要将上步生成的店做一些扰动,扰动\(\epsilon \sim N(0,\Psi)\).加入扰动后,得到黑色样本\(x^{(i)}\),如下: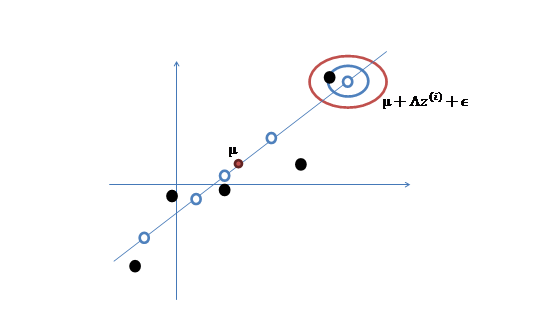
5.得到最终的训练样本,其中\(z,\epsilon\)均值均为0,因此\(\mu\)是原始样本点的均值。
为了方便大家理解,在此举一个实际中使用因子分析模型的例子。
在企业形象或品牌形象的研究中,消费者可以通过一个有24个指标构成的评价体系,评价百货商场24个方面的优劣。但消费者主要关心的是三个方面,即商店的环境、商店的服务和商品的价格。因子分析方法可以通过24个变量,找出反映商店环境、商店服务水平和商店价格的三个潜在因子,对商店进行综合评价。
由以上的直观分析,我们知道了因子分析其实就是认为高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的,因此高维数据可以使用低维来表示。
因子分析模型的推导
似然函数推导
上一节对因子分析模型进行了定义,以及从数据生成的角度对它进行了进一步阐述。本节则介绍上一节中定义的参数在模型中是如何被使用的。具体来讲,就是该模型对训练数据的似然函数是什么。
首先,重新列出模型的定义公式:
$$z \sim N(0,I) \\\ \epsilon \sim N(0,\Psi) \\\ x=\mu+\Lambda z + \epsilon$$
其中,误差\(\epsilon\)和隐含变量\(z\)是相互独立的。
使用高斯分布的矩阵表示法对模型进行分析。该方法认为z和x符合多元高斯分布,即:
$$\begin{bmatrix}z \\\ x \end{bmatrix} \sim N(\mu_{zx},\Sigma)$$
接下来就是求解\(\mu_{zx},\Sigma\)。
已知\(E[z]=0,E[\epsilon]=0\),则:
$$E[x]=E[\mu+\Lambda z + \epsilon]=\mu$$
故:
$$\mu_{zx}=\begin{bmatrix} \vec{0} \\\ \mu\end{bmatrix}$$
为了求解\(\Sigma\),需要计算:
$$\Sigma_{zz}=E[(z-E[z])(z-E[z])^T] \\\ \Sigma_{zx}=\Sigma_{xz}^T=E[(z-E[z])(x-E[x])^T] \\\ \Sigma_{xx}=E[(x-E[x])(x-E[x])^T]$$
根据定义,可知\(\Sigma_{zz}=Cov(z)=I\),另外:
$$\Sigma_{zx}=E[(z-E[z])(x-E[x])^T] \\\ =E[z(\mu+\Lambda z + \epsilon - \mu)^T] \\\ =E[zz^T]\Lambda^T+E[z \epsilon^T]=\Lambda^T$$
上述公式最后一步,\(E[zz^T]=Cov(z)=I\)。并且,\(z,\epsilon\)相互独立,有\(E[z\epsilon^T]=E[z]E[\epsilon^T]=0\)
$$\Sigma_{xx}=E[(x-E[x])(x-E[x])^T]=E[(\Lambda z+\epsilon)(\Lambda z + \epsilon)^T] \\\ =E[\Lambda z z^T \Lambda^T + \epsilon z^T \Lambda^T + \Lambda z \epsilon^T + \epsilon \epsilon^T] \\\ = \Lambda E[z z^T]\Lambda^T + E[\epsilon \epsilon^T]=\Lambda \Lambda^T + \Psi$$
将上述求解结果放在一起,得到:
$$\begin{bmatrix}z \\\ x \end{bmatrix} \sim N(\begin{bmatrix} \vec{0} \\\ \mu \end{bmatrix}, \begin{bmatrix}I \ \ \ \Lambda^T \\\ \Lambda \ \ \Lambda \Lambda^T + \Psi \end{bmatrix})$$
所以,得到x的边际分布为:
$$x \sim N(\mu, \Lambda \Lambda^T + \Psi)$$
因而,对于一个训练集\(\{x^{(i)};i=1,2…,m\}\),我们可以写出参数的似然函数:
$$\ell(\mu,\Lambda,\Psi)=log \prod_{i=1}^m \frac{1}{(2\pi)^{n/2}|\Lambda \Lambda^T + \Psi|^{\frac{1}{2}}} * \\\ exp \left(-\frac{1}{2}(x^{(i)}-\mu)(\Lambda \Lambda^T + \Psi)^{-1} (x^{(i)}-\mu)^T \right)$$
由上式,若是直接最大化似然函数的方法求解参数的话,你会发现很难,因而下一节会介绍使用EM算法求解因子分析的参数。
EM求解参数
因子分析模型的EM求解直接套EM一般化算法中的E-step和M-step公式,对于E-step来说:
$$Q_i(z^{(i)})=p(z^{(i)}|x^{(i)};\mu,\Lambda,\Psi)$$
前面我们已经得到条件分布的期望和方差:
$$\mu_{z^{(i)}|x^{(i)}}=\Lambda^T(\Lambda \Lambda^T +\Psi)^{-1} (x^{(i)}-\mu) \\\ \Sigma_{z^{(i)}|x^{(i)}}=I-\Lambda^T (\Lambda \Lambda^T + \Psi)^{-1} \Lambda$$
代入上面两个公式,可以得到\(Q_i(z^{(i)})\)的概率密度函数了,即:
$$Q_i(z^{(i)})=\frac{1}{(2\pi)^{k/2}|\Sigma_{z^{(i)}|x^{(i)}}|^{1/2}}exp \left(-\frac{1}{2}(z^{(i)}-\mu_{z^{(i)}}|x^{(i)})^T \Sigma^{-1}_{z^{(i)}|x^{(i)}}(z^{(i)})-\mu_{z^{(i)}|x^{(i)}}) \right) $$
在M-step中,需要最大化如下公式来求取参数\(\mu,\Lambda,\Psi\):
$$\sum_{i=1}^m \int_{z^{(i)}} Q_i(z^{(i)}) log \frac{p(x^{(i)},z^{(i)};\mu,\Lambda,\Psi)}{Q_i(z^{(i)})}dz^{(i)} \\\\
=\sum_{i=1}^m \int_{z^{(i)}} Q_i(z^{(i)}) [log \ p(x^{(i)}|z^{(i)};\mu,\Lambda,\Psi) +log \ p(z^{(i)}) - log \ Q_i(z^{(i)})] dz^{(i)} \\\\
=\sum_{i=1}^m E_{z^{(i)} \sim Q_i}[log \ p(x^{(i)}|z^{(i)};\mu,\Lambda,\Psi) +log \ p(z^{(i)}) - log \ Q_i(z^{(i)})]$$
具体求解只需要分别对上述式子参数求偏导,令偏导函数为0即可求解。

