　　本文主要介绍主成分分析算法(Principal Components Analysis,PCA)。该算法尝试搜寻数据所处的子空间，只需计算特征向量就可以进行降维。本文将尝试解释为什么通过特征向量计算能够实现降维。同时将介绍使用奇异值分解（SVD）方法来实现PCA求解。

引入

　　PCA解决了什么样的问题呢? 下面举一个例子来回答。
　　设想有一个数据集$\{x^{(i)};i=1,…,m\}$,其中$x^{(i)} \in \mathbb{R}^n $。比如每个$x$代表一辆车，$x$的属性可能是车的最高速度，每公里耗油量等。如果有这样两个属性，一个以千米为单位的最大速度，一个以英里为单位的最大速度。这两个速度很显然是线性关系，可能因为数字取整等缘故有一点点扰动，但不影响整体线性关系。因此实际上，数据的信息量是n-1维度的。多一维度并不包括更多信息。PCA解决的就是将多余的属性去掉的问题。
　　再考虑这样一个例子，直升飞机驾驶员。每个驾驶员都有两个属性，第一个表示驾驶员的技能评估，第二个表示驾驶员对驾驶的兴趣程度。由于驾驶直升机难度较大，所以一般只有对其有很大的兴趣，才能较好的掌握这项技能。因此这两个属性是强相关的。实际上，根据已有的数据，可以将这两个属性使用坐标图进行展示，如下：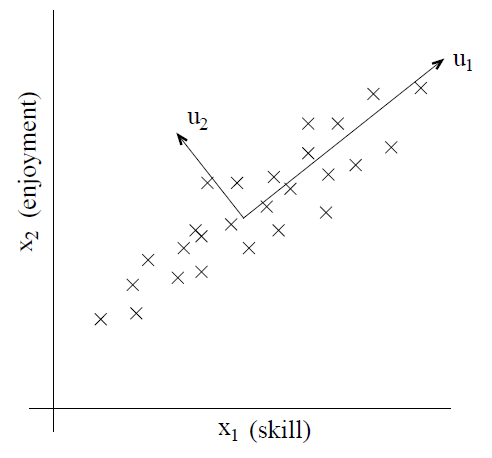

　　由图可知，$u_1$展示了数据的相关性，称为主方向；$u_2$则反映了主方向之外的噪声，那么如何计算出主方向呢？

预处理

　　运行PCA算法之前，数据一般需要预处理，预处理步骤如下：
1）令$\mu=\frac{1}{m}\sum_{i=1}^m x^{(i)}$
2) 使用$x^{(i)}-\mu替换x^{(i)}$
3）令$\sigma_j^2=\frac{1}{m} \sum_i (x_j^{(i)})^2$
4) 使用$\frac{x_j^{(i)}}{\sigma_j}替换x_j^{(i)}$
　　步骤1-2将数据的均值变成0，当已知数据的均值为0时，可以省略这两步。步骤3-4将数据的每个维度的方差变为1(此时均值已处理为0，故只需要求平方即可)，从而使得每个维度都在同一尺度都下被衡量，不会造成某些维度因数值较大而影响到。当预先知道数据处于同一尺度下时，可以忽略3-4步，比如图像处理中，已经预知了图像的每个像素都在0-255范围内，因而没有必要再进行归一化了。

PCA算法

直观理解

　　如何找到数据的主方向呢？在二维空间下可以这样理解，有一个单位向量u，若从原点出发，这样定义u以后就相当于定义了一条直线。每个数据点在该直线上都有一个投影点，寻找主方向的任务就是寻找一个u使得投影点的方差最大化。
　　那么问题来了。问题1，能不能不从原点出发？可以，但那样计算就复杂了，我们归一化时已经将均值变为0，就是为了在寻找方向的时候使向量可以从原点出发，便于计算。问题2，多维空间下，多个主方向时怎么办？那就是不止寻找一个单位向量了，找到一个主方向后，将该主方向的方差影响去掉，然后再找主方向。如何去掉前一个主方向的方差影响呢？对于二维数据来说，是将所有数据点在垂直于该主方向的另一个方向上做投影，比如上图，要去掉主方向$u_1$的方差影响，需要在$u_2$方向上进行投影，多维空间上也可以类推。
　　以方差最大化来理解寻找主方向的依据是什么？直观上看，数据初始时会有一个方差，我们把这个方差当作数据包含的信息，我们找主方向的时候尽量使方差在子空间中最大化，从而能保留更多的信息。
　　再举一个例子来说明如何寻找主方向。比如下面图中的五个点。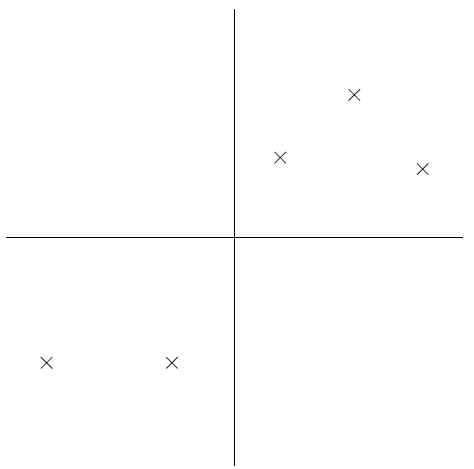

　　其中一个方向如下图所示: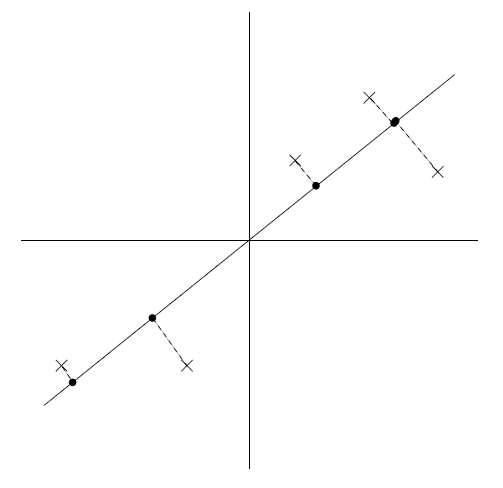

　　可以发现，上图中，直线上的黑点即原始数据在直线上的投影，投影的数据仍然保留着较大的方差。
　　相反如果取方向如下图所示：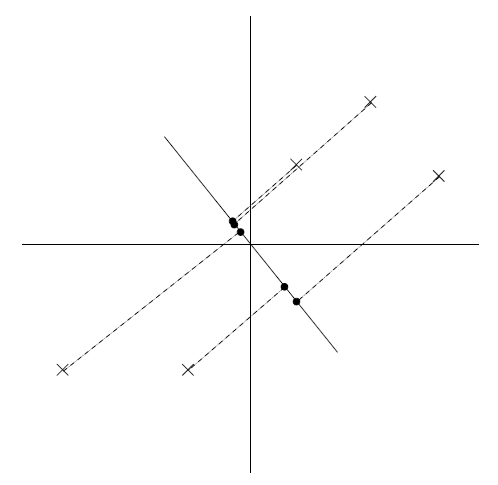

　　可以发现上图中，投影数据的方差很小。

形式化定义

　　下面给出求主方向的形式化定义。
　　假设给定一个单位向量$u$和点$x$,$x$到$u$的投影长度为$x^T u$,即点$x$在$u$上的投影点，到坐标原点的距离为$x^T u$.如下图所示: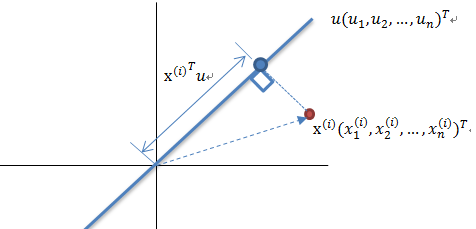

　　实际上就是向量内积。
　　因此，我们希望最大化投影方差，选择单位向量u使得下式最大化：
$$\frac{1}{m}\sum_{i=1}^m ({x^{(i)}}^T u)^2 = \frac{1}{m}\sum_{i=1}^m u^T x^{(i)} {x^{(i)}}^T u \\\\
=u^T \left(\frac{1}{m} \sum_{i=1}^m x^{(i)} {x^{(i)}}^T \right)u$$
　　上述平方展开可以根据$X^2=X^T X$得到，即$({x^{(i)}}^T u)^2=({x^{(i)}}^T u)^T ({x^{(i)}}^T u)=u^T x^{(i)} {x^{(i)}}^T u$
　　注意到，对于归一化后的数据，其投影点的均值也为0，因而才可以在方差的计算中直接平方。另外，该公式有一个约束条件,即$||u||_2=1$。
　　首先是协方差矩阵$\Sigma=\frac{1}{m}\sum_{i=1}^m x^{(i)} {x^{(i)}}^T$的理解。假设我们有两个特征a和b，有m个样本，则数据集表示为：
$$X^T=\begin{bmatrix} —-x^{(1)}—- \\\ —-x^{(2)}—- \\\ … \\\ —-x^{(m)}—- \end{bmatrix}=\begin{bmatrix} a_1 \ b_1 \\\\a_2 \ b_2 \\\ … \\\ a_m \ b_m \end{bmatrix}$$
　　则：
$$X=\begin{bmatrix}|　\ 　|　\ …　 \ | \\\\　 x^{(1)} \ x^{(2)}\ … \ x^{(m)} \\\\　 |　\ 　|　\ …　\ | \end{bmatrix}=\begin{bmatrix} a_1 \ a_2 \ … \ a_m \\\\b_1 \ b_2 \ … \ b_m \end{bmatrix}$$
　　则:
　　$$\Sigma=\frac{1}{m}\sum_{i=1}^m x^{(i)} {x^{(i)}}^T=\frac{1}{m}XX^T=\begin{bmatrix}\frac{1}{m} \sum_{i=1}^m a_i^2　\ \frac{1}{m} \sum_{i=1}^m a_i b_i \\\ \frac{1}{m} \sum_{i=1}^m a_i b_i　 \ \frac{1}{m} \sum_{i=1}^m b_i^2 \end{bmatrix}$$
　　这个最大化问题的解就是矩阵$\Sigma=\frac{1}{m}\sum_{i=1}^m x^{(i)} {x^{(i)}}^T$的特征向量。这是如何得到的呢？如下。
　　使用拉格朗日方程求解该最大化问题，则：
$$\ell=u^T \left(\frac{1}{m} \sum_{i=1}^m x^{(i)} {x^{(i)}}^T \right)u-\lambda(||u||_2-1)=u^T \Sigma u - \lambda(u^Tu-1)$$
　　对u求导：
$$\nabla_u \ell=\nabla_u(u^T \Sigma u -\lambda(u^Tu-1))=\nabla_u u^T\Sigma u-\lambda \nabla_u u^T u \\\\
=\nabla_u tr(u^T\Sigma u)-\lambda \nabla_u tr(u^T u)=(\nabla_{u^T}tr(u^T \Sigma u))^T-\lambda(\nabla_{u^T}tr(u^T u))^T \\\\
={(\Sigma u)^T}^T-\lambda{u^T}^T=\Sigma u-\lambda u$$
令倒数为0，可知u就是$\Sigma$特征向量。
　　因为$\Sigma$是对称矩阵，因而可以得到相互正交的n个特征向量$U^T=\{u^1,u^2,…,u^n\}$,那么如何达到降维的效果呢？选取最大的k个特征值所对应的特征向量即可。降维后的数据可以用如下式子来表达：
$$y^{(i)}=U^T x^{(i)}=\begin{bmatrix}u_1^T x^{(i)} \\\ u_2^T x^{(i)} \\\ … \\\ u_k^T x^{(i)}\end{bmatrix}$$
　　注意到，实际上通过特征向量来降维能够保证投影方差最大化，这也是我们的优化目标。

PCA的应用

　　压缩与可视化，如果将数据由高维降至2维和3维，那么可以使用一些可视化工具进行查看。同时数据的量也减少了。
　　预处理与降噪，很多监督算法在处理数据前都对数据进行降维，降维不仅使数据处理更快，还去除了数据中的噪声。是的数据的稀疏性变低，减少了模型假设的复杂度，从而降低了过拟合的概率。
　　具体的应用中，比如图片处理，对于一个100*100的图片，其原始特征长度为10000，，使用PCA降维后，大大减少了维度，形成了“特征脸”图片。而且还减少了噪声如光照等影响，使用PCA降维后的数据可以进行图片相似度计算，在图片检索中和人脸检测中都能达到很好的效果。

奇异值分解（SVD）

　　奇异值分解时PCA的一种实现。前面我们提到PCA的实现手段是通过计算协方差矩阵$\Sigma=\frac{1}{m} \sum_{i=1}^m x^{(i)} {x^{(i)}}^T$,然后对其特征值与特征向量进行求解。这样做的不好地方在于，协方差矩阵的维度是样本维度×样本维度。比如对于100×100的图片来说，如果以像素值作为特征，那么每张图片的特征维度是10000，则协方差矩阵的维度是10000×10000。在这样的协方差矩阵上求解特征值，耗费的计算量呈平方级增长。利用SVD可以求解出PCA的解，但是无需耗费大计算量，只需要耗费（样本量×样本维度）的计算量。下面介绍SVD:
　　SVD的基本公式如下：
$$A=UDV^T$$
　　即将$A$矩阵分解为$U,D,V^T$矩阵。其中，$A \in \mathbb{R}^{m*n}, U \in \mathbb{R}^{m*n}, D \in \mathbb{R}^{n*n}$，且$D$为对角矩阵，D对角线上的每个值都是特征值且已按照大小排好序，$V^T \in \mathbb{R}^{n*n}$。其中，U的列向量即是$AA^T$的特征向量，V的列向量是$A^TA$的特征向量。SVD的原理可以参见【参考】一节的知乎回答。令：
$$A=X=\begin{bmatrix}|　\ 　|　\ …　 \ | \\\\　 x^{(1)} \ x^{(2)}\ … \ x^{(m)} \\\\　 |　\ 　|　\ …　\ | \end{bmatrix}$$
　　因此计算量为X矩阵，即原始样本矩阵的大小。由前可知，协方差矩阵$\Sigma=\frac{1}{m}XX^T$,那么U矩阵恰好为PCA的解。将PCA转化为SVD求解问题后，就可以进行加速了。因为SVD的求解有其特定的加速方法。本文不涉及。
　　SVD可以理解为PCA的一种求解方法。SVD也可以用于降维，一般情况下，D对角线中的前10%或20%的特征值已占全部特征值之和的90%以上。因而可以对$UDV^T$三个矩阵各自进行裁剪，比如将特征由n维降为k维。那么$U \in \mathbb{R}^{m*k}, D \in \mathbb{R}^{k*k}, V^T \in \mathbb{R}^{k*n}$即可。
　　在SVD的最后，Ng总结出一张表如下：

　　表格中的内容很好理解，Ng特地强调的是这样的思考方式，寻找算法中的相同点和不同点有利于更好的理解算法。
　　最后给出两个参考，ZCA白化和PCA白化和PCA的数学原理。这两个资料对于理解PCA非常有帮助。

参考

斯坦福大学机器学习视频教程
 知乎：为什么PCA可以通过求解协方差矩阵计算，也可以通过分解内积矩阵计算？
ZCA白化和PCA白化
 PCA的数学原理