基于张量分解的POI协同过滤推荐算法

本文是对论文《Collaborative Location Recommendation by Integrating Multi-dimensional Contextual Information》的读书报告。这是一篇使用张量分解来推荐POI的论文笔记。

背景

本文研究的领域是Point-of-Interest(POI) Recommendation.这是一种新型的推荐任务，和目前流行的、基于位置的的社交网络（LBSN）相关联。借助于LBSN应用的爆发式增长和无线通信技术的提升，目前人们经常会通过LBSN服务和朋友交流、发现地点，共享信息。和传统的推荐任务不同的是，POI更关注于推荐的个性化和上下文感知能力，以此提升用户体验。最普遍的上下文信息包括地理和社交信息。目前主流的一些方法利用用户的社交约束、地理和时间影响进行建模，并且考虑的上下文信息越越周全，通常性能也越好。因此目前的研究主要集中在如何集成多种多样的上下文信息。但是，利用签到数据进行建模的方案不多。

动因

随着签到数据（check-in data）的增长，亟需开发出一种更有效的POI推荐应用，能够建模和集成多种类型的上下文信息，尤其是时间信息。本文基于此，提出了一种基于张量分解的协同过滤方案，能够建模多维度的上下文信息。比起传统的基于user-location的矩阵分解模型，本文提出的TenMF张量分解模型利用更高维度的张量，将签到数据的时间信息集成到上下文信息中，具体而言就是user-location-time三个维度的张量。基于这个模型，本文还创造性的引入了用户和地点内部的关系信息，即用户社交影响力和地点的空间相似性，作为隐变量的正则化项，提高模型的推荐准确性。

TenMF的优势包括：

建模用户的签到活动，将签到数据中的时间维度信息纳入user-location-time矩阵,使得数据的表示更加完备。
基于张量分解的方法是传统矩阵分解的扩展，因此沿袭了矩阵分解的诸多优势，如计算简便、对稀疏数据鲁棒等。
易于扩展，方便集成更多的上下文信息，形成更高阶的张量。

本文主要贡献包括：

本文会详尽阐述多维度的上下文信息是如何提高POI推荐系统的性能，并提出一种利用高阶统一张量来集成多维度的上下文信息的方法。上下文信息来自签到数据中的空间影响力、时序依赖性、用户社交约束。这种方法能够用来解决用户动态签到活动中的时序依赖性问题。
本文会系统的阐述张量分解目标函数的设计和生成过程。本文创新的引入辅助信息，社交和空间信息，作为目标函数的正则化项。并且，提出的方法能够很灵活的集成更多的辅助信息。
本文会使用真实的数据集对提出的模型进行评估。实验结果表明了模型的有效性。

主要思想

本文提出的TenMF模型，采用高阶的张量来表示签到数据中的Users、Locations、Time三者之间的关系，同时集成更丰富的上下文信息。最终建模成一个统一的、包含正则化项的张量分解方案，用于预测用户对某个地点的签到概率，从而解决POI推荐问题。另外，该方案中的正则化项采取图拉普拉斯矩阵解法，从用户社交约束和地点空间相似矩阵中推导而来。

【We specially present a unified, regularized tensor factorization method along with graph Laplacians induced from users’ social constraints and spatial proximity to predict the check-in probability of a location and to finally solve the POI recommendation problem.】

基于张量的签到数据表示

问题形式化定义

给定历史签到记录，$m$ users ${u_i}_{i=1}^m$ on $n$ locations ${v_j}_{j=1}^n$ and $q$ time frames ${t_k}_{k=1}^q$ , 给目标用户推荐其可能感兴趣的地点集合。
张量表示

使用张量$R \in \mathbb{R}^{m×n×p}$，$R_{ijk}$代表用户$u_i$在$t_k$时段访问地点$v_j$的次数。
优化目标

使用张量分解技术求解$R$的最佳估计$\hat{R}$。其中$\circ$是张量积（外积操作），$D$是隐变量的维度数，目标是找到原始张量R（可能是稀疏、有缺失值的）的最佳估计$\hat{R}$.
$$
\hat{R} = \sum_{d=1}^D u_d \circ v_d \circ t_d
$$
上述张量分解，可使用下述优化目标，迭代求解。如下：
$$
\ell(U,V,T) = \frac{1}{2} \mathop{min}_{U,V,T} ||R -\sum_{d}^D u_d \circ v_d \circ t_d ||^2_F \\
u_d \in \mathbb{R}^m, v_d \in \mathbb{R^n}, t_d \in \mathbb{R^q}
$$
加入防止过拟合的参数正则化项后：
$$
\ell(U,V,T) = ||R-\hat{R}||^2_F + \lambda(||U||^2_F + ||V||^2_F + ||T||^2_F) \\
U = [u_1, …u_D]\in \mathbb{R}^{m \times D}、V= [v_1, …v_D]\in \mathbb{R}^{n \times D}、T = [t_1, …t_D]\in \mathbb{R}^{q \times D}
$$

集成上下文正则化项

虽然上述3个正则化项对于低秩近似足够，但是这里仍然加入更多的先验假设。许多情况下，不仅仅是研究对象之间的关系信息很重要，而且对象本身的内部上下文信息也很重要。就我们的研究问题而言，不仅仅User、Location、Time三者之间的关系很重要，同时User内部的信息，如User mutual friendships，Location内部的信息，如Location proximity也很重要。加入这些自身内部信息到正则化项中，能够有效提高模型的性能。

User Mutual Friendship

朋友之间倾向于相似的行为，因为他们可能兴趣相同，签到数据中可能隐藏着较强的潜在“结伴签到“的关联信息。因此，借助于朋友可能能够提供很好的推荐。
Location Proximity

用户倾向于访问一个局部领域范围内的地点，因此借助相似地点可能能够提供好的推荐。

集成上述两个因子，可以借助“谱聚类“中的思想。对于互为朋友的用户或互为邻近点的地点，应当使得双方分解后的隐表示（Latent Representations）更为接近。因此这里的关键是构造相似矩阵。
$$
\mathop{min}_{U,V,T} \ell = ||R-\hat{R}||^2_F +\lambda_1\sum_{i=1}^m \sum_{j=1}^m A_{ij} ||U_{i*}-U_{j*}||^2 + \lambda_2 \sum_{i=1}^n \sum_{j=1}^n B_{ij} ||V_{i*}-V_{j*}||^2 \ + \lambda_3(||U||^2+ ||V||^2 + ||T||^2)
$$

$A_{ij}$是$u_i$和$u_j$的社交联系程度。$B_{ij}$是$v_i$和$v_j$的地点相似程度。
$$
A_{ij} \propto s_{ij}^f = \eta_s \frac{|F_i \cap F_j|}{|F_i \cup F_j|}+ (1-\eta_s)\frac{|L_i \cap L_j|}{|L_i \cup L_j|} \
s.t. j \in N_i
$$
$A_{ij}$的计算考察两个方面的影响因素，1是共同的好友，2是共同签到的地点。$\eta_s$是二者的比重.

注意上述，$N_i$是指$u_i$的领域Neighborhood。因此，相当于只考察和$u_i$邻近的用户$u_j$. 个人认为相当于需要设置一个阈值，$A_{ij}$小于阈值的属于领域，大于阈值的相似性直接设置为0。
$$
B_{ij} \propto \frac{1}{dis(v_i, v_j)} \\
dis(v_i, v_j) = r \times \Delta \hat{\sigma} \\
\Delta \hat{\sigma} = arccos(sin \phi_i sin \phi_j + cos \phi_i cos \phi_j cos(\Delta \lambda)) \\
s.t. j \in N_i
$$
$B_{ij}$的计算只需要考察地点的实际物理距离（考虑地球是圆球体，因此实际物理距离有别于两点之间的直线距离）。相似性正比于距离的倒数。

注意上述，$N_i$是指$v_i$的领域Neighborhood。因此，相当于只考察和$v_i$邻近的地点$v_j$。个人认为相当于需要设置一个阈值，$B_{ij}$小于阈值的属于领域，大于阈值的相似性为0。

优化目标改写成如下：（和谱聚类优化目标很像,从相似矩阵导出拉普拉斯矩阵，转成拉普拉斯矩阵的迹表达式）
$$
\mathop{min}_{U,V,T} \ell = ||R-\hat{R}||^2_F +\lambda_1\sum_{i=1}^m \sum_{j=1}^m A_{ij} ||U_{i*}-U_{j*}||^2 + \lambda_2 \sum_{i=1}^n \sum_{j=1}^n B_{ij} ||V_{i*}-V_{j*}||^2 \ + \lambda_3(||U||^2+ ||V||^2 + ||T||^2) \
= ||R-\hat{R}||^2_F + \frac{\lambda_1}{2}tr(U^T L_U U) + \frac{\lambda_2}{2} tr(V^T L_V V) + \lambda_3(||U||^2+ ||V||^2 + ||T||^2) \\
= ||R-\hat{R}||^2_F + tr[U^T (\lambda_3 I + \lambda_1L_U) U] + tr[V^T(\lambda_3 I + \lambda_2 L_V) V] + \frac{\lambda_3}{2}(TT^T)
$$
上述，$L_U$是$A$的拉普拉斯矩阵，$L_V$是$B$的拉普拉斯矩阵。

优化

上述目标函数是non-convex的，因此使用迭代算法能够找到最优解。共有3个要求解的矩阵$U,V,T$, 每次迭代时，固定其余两个，迭代其中一个。使用梯度下降法直到收敛。

更新$U$

此时，$V,T$可看成常数矩阵，目标重写为：

$$
\ell(U,V,T) = \frac{1}{2} (R_{(1)}-U(V \odot T)^T)^T (R_{(1)}-U(V \odot T)^T)\ + \frac{\lambda_1}{2} tr(U^TL_U U) + \lambda_3 ||U||_F^2 $$

其中，$R_{(1)}$是张量$R$的mode-1 matricization。$\odot $是矩阵的$Khatri-Rao$积。$*$是$Hadamard$积。

计算梯度：
$$
\nabla_U \ell(U,V,T) = -R_{(1)}(V\odot T) + U[(V^TV)*(T^TT)] + \lambda_1 L_U U+ \lambda_3 U \ = -U(V \odot T)^T(V\odot T) + U[(V^TV * (T^T T))] + \lambda_1 L_U U + \lambda_3 U $$

更新$V$

类似。
更新$T$

类似。

算法步骤：

上述学习率$\delta$，本文中采取每迭代步折扣$0.9$的策略进行动态改变。

实验验证

实验目的和指标

目的

评估模型对POIs的预测和推荐性能。

【Evaluate how well the proposed method can recover the POIs in the testing data for a given user at a given time.】

指标
- $Precision@x$
  
  对每个用户，评估推荐的前$x$个POIs中属于此前划分出来的测试集POIs的个数占所有推荐的POIs的比例。
- $Recall@x$
  
  对每个用户，评估推荐的前x个POIs中属于此前划分出来的测试集POIs的个数占测试集中所有POIs的比例。
上述指标需要先对每个时间slot进行评估。即$Precision@x(t)、Recall@x(t)$

总体的precision和recall对24个时间slot进行平均。即：
$$
Precision@x = \frac{1}{24}\sum_{t=1}^{24}Precision@x(t) \\
Recall@x = \frac{1}{24}\sum_{t=1}^{24}Recall@x(t)
$$

数据处理

数据集

两个著名的社交网站收集的数据。包括，用户在该平台上签到留下的位置痕迹；用户的关系数据。

1） Location-based social networking website where users share their locations by checking-in.

2） The friendship network is undirected and was collected using their public API.
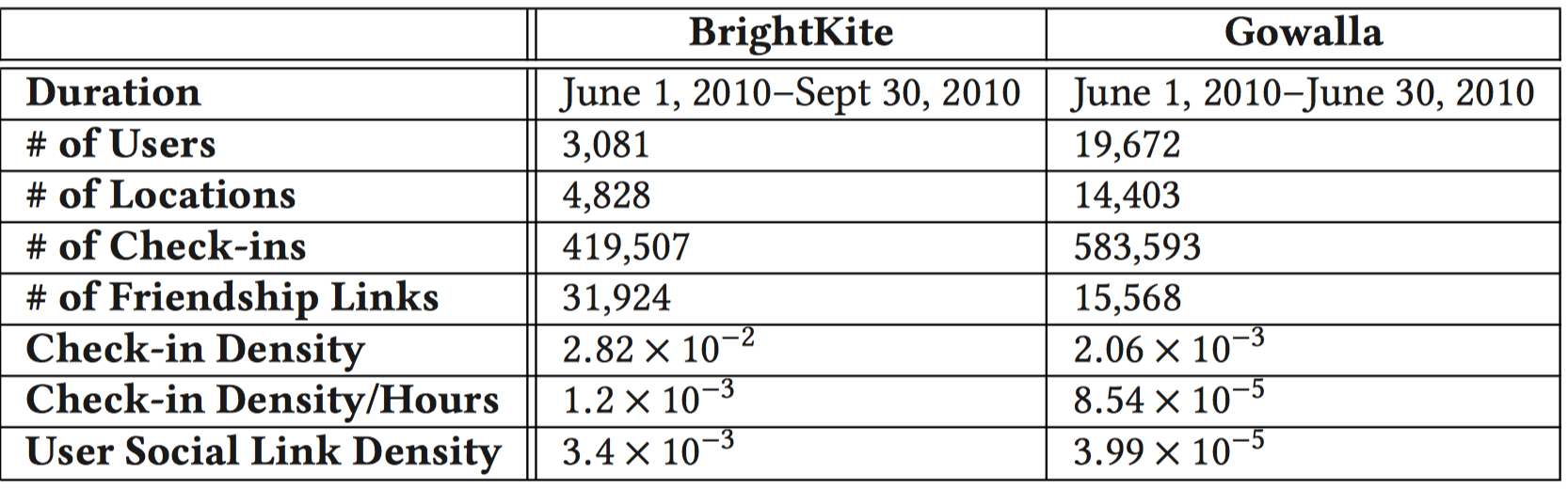
- Brightkite: 2010.6.1~2010.9.30。3081Users, 4828 Locations, 419507 Check-ins, 31924 Friendship links.
- Gowalla: 2010.6.1~2010.6.30。19672 Users, 14403 Locations， 583593 Check-ins, 15568 Friendship links.
数据预处理
- 剔除签到地点少于10个的用户。
- 剔除被签到次数少于10个的地点。
- 将数据按照”小时”分成24个slots。
- 某个地点的签到次数通常变化差异很大，因此进行区间缩放到$[0,1]$, 采取$\frac{1}{1+1/r}$，其中r是原始数据集的访问次数。
- 文中给出的模型是基于离散Location的。而数据集中给出的位置信息是连续型经纬度值。因此需要进行离散化处理。（这部分论文没有明说，个人认为可以进行分箱处理离散化，或者使用开源API库将经纬度转成某个具体粒度下的离散地点。不过数据集中也有location id字段，直接可以作为离散地点）
最终处理后的数据【疑惑1】
划分测试集
- 对每个用户，划分出该用户签到地点的20%出来作为测试集，评估模型的性能。

实验方法

对比实验。
将提出的模型Tensor Factorization-based location Recommendation(TenMF)和目前最先进的12种模型进行对比。
实验分成两组进行，第一组为不考察时间信息的模型；第二组为考察时间信息的模型。
第一组：不考察时间信息的模型包括：
- NMF: 非负矩阵分解模型
- User-CF：基于用户的协同过滤模型，推荐和该用户相似的人群的兴趣点。
- Item-CF：基于物品的协同过滤模型，推荐和用户去过的地点相似的地点。
- Friendship-aware：推荐用户的朋友所去过的地方。这个方法和User-CF类似，只不过这里参考的用户是用户真实的朋友集，考察了上下文信息；而User-CF参考的用户是根据User-Item矩阵计算出来的相似用户集，未考察上下文信息。
- Geographical-aware: 使用GMM建模，实际上是对地点进行聚类，发掘空间聚集现象。可把不同的地点中心看成不同的高斯分布，每个地点中心代表一种地区偏好。核心思想是，对不同用户建模，某个用户对某个单一地点的偏好，可能源自多个地区偏好的融合。目标是挖掘分离出这些用户的地区偏好。作者在GMM基础上引入Dirichlet先验，好处是不需要显示指定GMM中高斯分布的个数。
- Linear Model。线性加权上下文信息。社交、时间、空间影响力。
第二组：考察时间信息的模型包括：
- User-based Time: User-CF基础上加上时间。即在某个时间，给用户推荐POI，参考相似用户在该时间gap内的兴趣点。
- Item-based Time：Item-CF基础上加上时间。参考和该用户去过的地点中在该时间gap内，相似的其他兴趣点。
- Time-aware：Item-based Time的变种。加入用户对更细粒度的时间偏好。
- BasicTenMF：不考虑用户社交影响力和地点相似性的Tensor Factorization-based location Recommendation.
- TenMF+Social：BasicTenMF基础上，考虑用户社交影响力。
- TenMF+Spatial：BasicTenMF基础上，考虑地点相似性。

实验过程

首先进行不同模型的对比实验，包括：

对于第一组不考察时间的模型
- 将本文提出的TenMF和第一组模型进行对比。
- 由于第一组模型不考察时间信息，因此需要将原始的三维数据user-location-time张量进行处理，使其能够应用到这些模型中。具体而言，就是按照time维度切分成24份，每份代表该时间slot内的user-location matrix,这样就能应用模型进行预测。最后再平均所有slots的推荐性能。
- TenMF按照上述“实验目的和指标”提到的方法进行性能评估。
对于第二组考察时间的模型
- 直接应用模型和指标公式计算评价指标。对比性能。

接着进一步考察本文提出的模型TenMF的性能影响因素，包括：

考察TenMF不同时间粒度的性能（不同的Number of Time Slots）；
TenMF分解得到的隐矩阵不同维度数的性能（指分解得到的隐矩阵的维度或隐因子的数量）。
正则化参数选择。

上述实验在两个数据集上都进行对比。

实验结果和分析

不同模型的对比实验
- 第一组不考察时间的模型对比
  - 下图(a)、(b)是数据集BrightKite上的性能对比。下图(c)、(d)是数据集Gowalla上的性能对比。
  - TenMF模型几乎在所有指标上均超过其他模型的性能，包括考察上下文信息和不考察上下文信息的模型；另外，基于上下文信息的模型(FA、GA、LIM、TenMF)性能整体上好于不基于上下文信息的模型(NMF、UCF、ICF)。
  - 有趣的是，UCF和ICF也好于NMF，可能是因为NMF比较适合于User-Location矩阵，并且没考虑任何上下文信息、没考虑过拟合等。
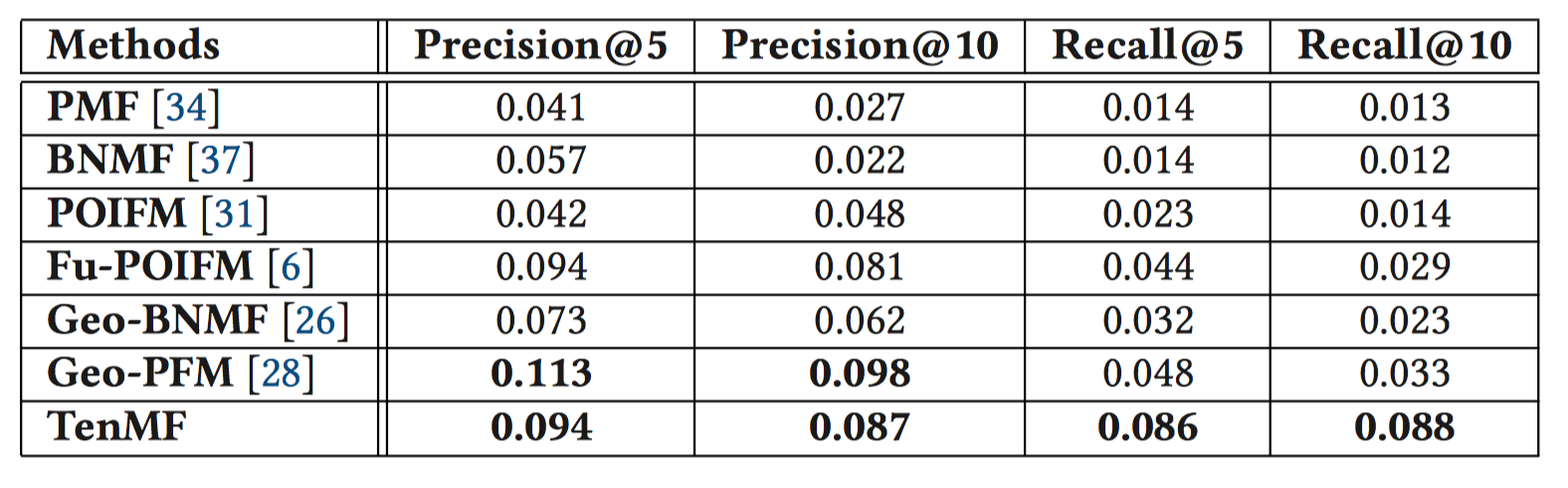
  - 另外，还在Gowalla上，将TenMF和目前最先进的概率模型进行对比。除了Geo-PFM在精确率上略胜于TenMF, TenMF比其他模型性能都好。【疑惑2】
- 第二组考察时间的模型对比
  - 下图(e)、(f)是BrightKite上的性能对比。下图(g)、(h)是Gowalla上的性能对比。
  - 基于张量分解的方法在BrightKite数据集上，大大超过了其他方法的性能，即使数据划分成不同的Time Slots后变稀疏了，模型的鲁棒性仍然很强。
  - 但是在Gowalla的Precision@15和@20上，TenMF的方法略微不如BasicTenMF。可能原因是，Gowalla数据集更加稀疏，导致社交影响力正则项不足以校正预测结果。另一方面,
    
    BasicTenMF+Spatial比BasicTenMF略好，意味着在该数据集上，空间影响力因子比社交影响力因子占更多主导地位。
不同时间粒度的对比实验
- 考察TenMF不同时间粒度下的性能，如(i)图所示。
- 可以看出，随着Time Frame的增大，Precision性能越好。可能由于随着Time Frame的增大，更多的判别信息和签到数据能够整合在一起，同时使得数据密度增大。这俩方面对预测精确度性能都有所帮助。然而，随着Time Frame的增大，Recall性能却变差了。同时，Time Frame增大会导致时间维度下降。然而从整体上而言，在某些例子中，Time Frame增大虽然导致Recall减小，但是总体性能是提高的【疑惑4】。
不同参数维度的对比实验
- 参数维度代表分解后得到的隐因子（Latent Factor）的数量。
- (k)、(l)展示了BrightKite上，不同参数维度的性能影响情况。
- 一开始随着参数维度的增加，性能有所提升，可能是由于参数维度的增加使得能更好得挖掘签到数据信息，提高性能。但是当超过35维度之后，性能开始下降，可能是由于过拟合造成的。

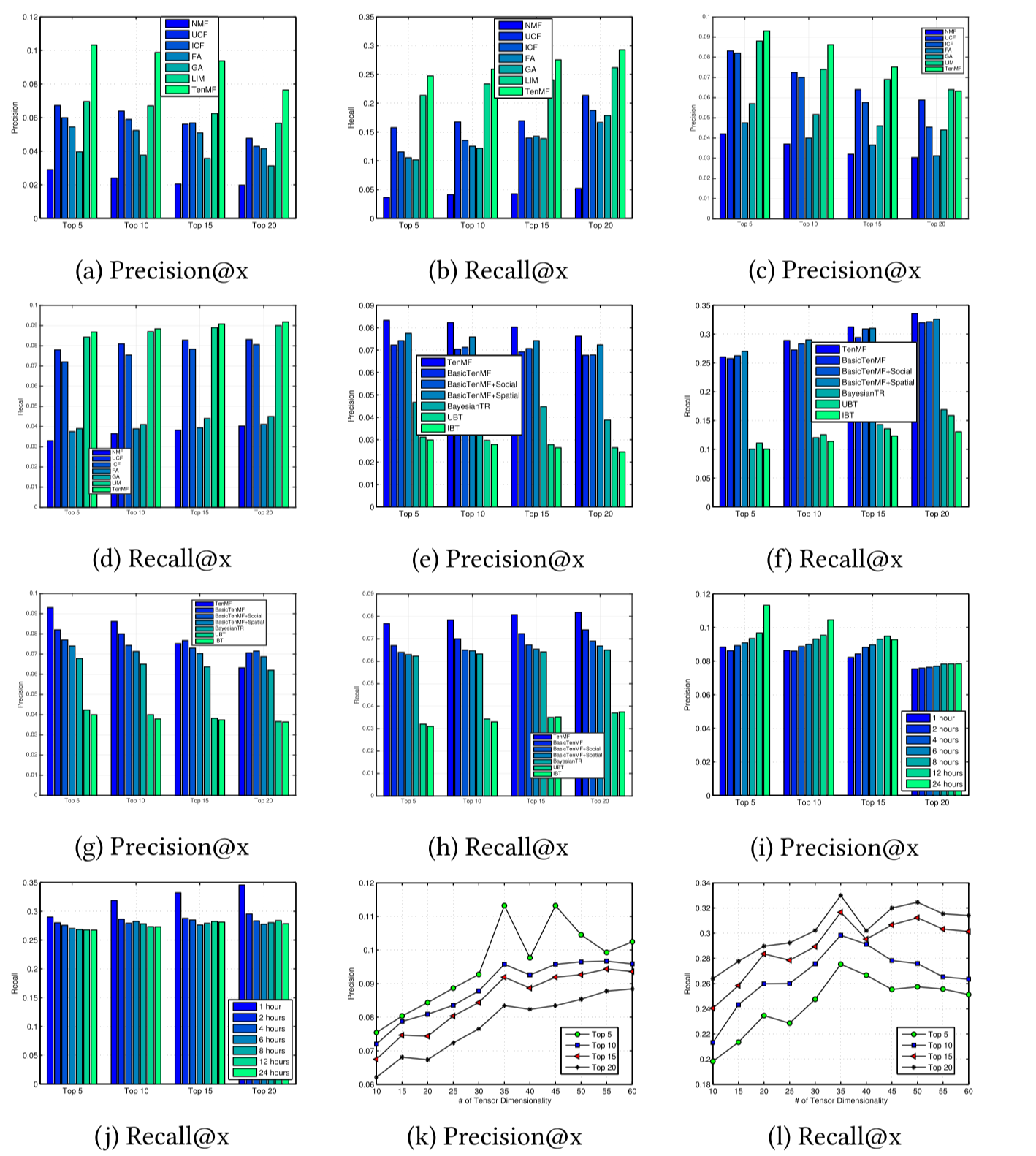
不同正则化参数的对比实验
- 作者最后还做了不同正则化参数$\lambda$下的模型性能，发现模型性能对$\lambda$还是比较敏感，因此需要进行调参，选择最佳的参数。
作者最后还讨论了TenMF的时间复杂度。TenMF的时间复杂度是$O(K(mnq))$, m,n,q分别是三个矩阵的维度，K是迭代的次数。作者引入alternating direction method of multipliers (ADMM)方法进行改进。除了计算效率有所改进，在性能上也有略微的提升。

结论

模型方案

本文提出了一种基于张量分解的POI推荐方案，该方案将用户社交约束和空间影响因素作为正则化项进行考虑。具体而言，将POI的签到数据作为第三维张量，并采用张量分解的方法来保证高维空间下POI推荐的有效性；同时还提出将上下文对象内部的关联信息作为张量分解优化目标中的正则化项，来提高推荐的准确性。

【We have proposed a novel POI recommendation approach based on tensor factorization with users’ social constraints and spatial influence as regularization terms.】

模型性能

本文提出的方案在两个真实数据集的实验中表现出了良好的性能，超过了目前主流的一些方法。

未来改进方向
- 优化算法改进：SGD的替代方法、并行张量分解。
- 考察更多的时间模式：如领域时间槽数据的相关性、签到数据中的周期性关系。
- 使用更多的数据集验证模型性能，同时和目前的POI推荐方案进行对比实验。

疑惑

数据点的密度是怎么计算的？

The densities of the BrightKite and Gowalla datasets after splitting are $1.2 × 10^{−3}$ and $8.54 × 10^{−5}$ ,

密度=数量/总面积吗？

作者将TenMF和概率模型进行对比时，只在Gowalla上进行比较，是不是说明有可能BrightKite上的性能不如概率模型？
上述Gowalla上的Precision和Recall量级大概不到10%。看来推荐系统性能提高只要超过1%，说明就有很大提升了。
既然上述不同时间粒度的模型对Precision和Recall性能有影响，那能不能做一个时间粒度动态变化的集成模型来满足对Precision和Recall的折中？
文章考察了User内部的关联信息User mutual Friendship，Location内部的关联信息Spatial Proximity. 但是没有考虑时间窗Time Frame内部的关联信息，如Temporal Correlations等。可以作为改进思路。
这篇文章涉及的张量分解知识，有别于矩阵分解。需要进一步学习研究。