LSTM+CRF NER

本文将借鉴论文《End-to-end Sequence Labeling via Bi-directional LSTM-CNNs-CRF》中的思路和方法实现命名实体识别。

目标

NER英文命名实体识别的目标是识别句子中每个词语的实体类型，包括5大类：PER(人名)、LOC(地名)、ORG(组织名)、MISC(其它类型实体)、O(非实体)。由于实体可能是由多个词语构成的，因此使用标注B、I来区分该词语是该实体的起始词(Begin)还是中间词(Inside)。示例如下：

1 2	John lives in New York and works for the European Union B-PER O O B-LOC I-LOC O O O O B-ORG I-ORG

命名实体识别最简单的实现方法就是查表法。也就是说，将所有的实体都标注好写进词典里，要识别句子中的实体时，直接查询词典，取出对应的词语的实体类型就可以了。但是问题在于，一方面实体数量太过于庞大，另一方面，会不断有新的实体出现，那么使用查表法就解决不了了。

通常，人类识别实体的方法是根据实体所处的上下文信息来判断的，因此为了模仿人类这种能力，此处主要使用神经网络的方法来进行实体识别。具体的方法是LSTM+CRF。LSTM用于建模、提取和利用上下文词语级别的信息，单个词内的字符级别的特征，CRF将利用提取到的特征以及标签信息，建模提取到的特征之间、标签之间、以及特征与标签之间的联系。二者结合起来实现命名实体任务。另外单个词内的字符级别的特征也可以采用论文中描述的CNN来提取，此处使用LSTM提取。

词语特征表示

神经网络的输入是句子，输出为句子中每个词的实体类型。为了使用神经网络建模，输入句子需要提取特征。特征包含两个方面，一方面是句子内词语级别的特征，另一方面是词语内字符级别的特征。前者是因为实体的识别依赖于上下文词语的特征；后者是因为实体的识别还依赖于自身的特征（如大小写等）。这两种特征都不需要手动设计，都使用神经网络来学习向量化表示。不过，对于词语的向量化表示，论文中会利用到预训练好的Glove词向量，不进行额外学习（最多Finetune一下）。对于字符的向量化表示，论文中使用CNN来提取特征，此处我们采用LSTM来提取特征。

下图是使用Bi-LSTM提取字符级别的特征。对于某个单词$w_i$(例如CAT)，$w = [c_1, \ldots, c_p]$，每个字符$c_i$都有一个向量化表示。使用Bi-LSTM建模单词字符词向量序列，并将Bi-LSTM最后输出的隐藏层$h_1、h_2$向量(前向、后向各一个)连接起来，作为该词$w_i$字符级别的特征，该特征能够捕获$w_i$形态学特点。

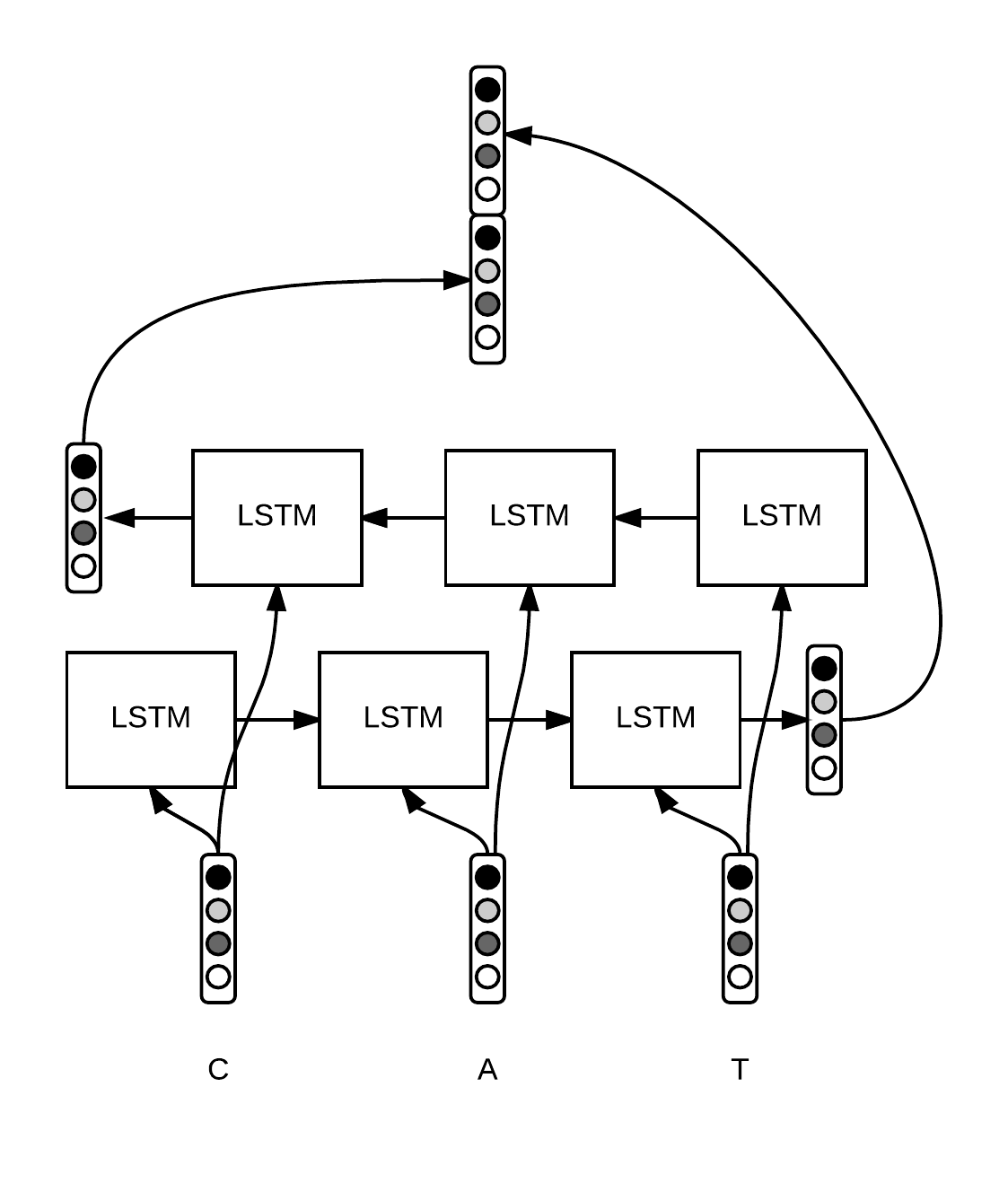
然后，再将提取到的字符级别的特征和Glove预训练好的词语级别的特征连接起来，作为该词最终的特征。

代码上，

下面针对的都是1个batch进行优化时，如何获取batch中的不同序列中的特征。

词向量：

将句子看成序列，序列由词语构成，词语看成序列不同时刻的观测输入。
- 为不同时刻的观测输入设置id，这里也就是为词语设置id。目的是查找观测的向量化表示。
  1
  2
  # shape = (batch size, max length of sentence in batch)
  word_ids = tf.placeholder(tf.int32, shape=[None, None])
  这里针对的是1个batch，batch由多个序列（句子）构成。要设置不同序列不同时刻的观测的id，也就是不同句子不同单词的id。因此word_ids的shape是二维的，$\text{Batch Size} \times \text{Sentence Length}$，Batch Size是这个Batch中序列的数量，Sentence Length是序列的最大长度，每个元素代表某个序列某个词语的id。
- 为不同序列设置有效长度，这里也就是句子的单词数目。目的是记录batch中不同序列的有效长度。
  1
  2
  # shape = (batch size)
  sequence_lengths = tf.placeholder(tf.int32, shape=[None])
  针对1个batch，记录batch中不同序列的有效长度。sequence_lengths一维数组记录了batch中不同句子的有效长度，即，每个元素记录了对应序列句子的单词真实数目。之所以称作有效长度，是因为word_ids中第二维是最大序列长度，而不同句子长度不一样，因此第二维不是全部填满的，末尾大部分为0，因此使用sequence_length记录一下每条序列的有效长度。
- 根据上述的id查询观测词语的向量化表示。
  1
  2
  3
  L = tf.Variable(embeddings, dtype=tf.float32, trainable=False)
  # shape = (batch size, sentence, word_vector_size)
  pretrained_embeddings = tf.nn.embedding_lookup(L, word_ids)
  $L$就是词向量矩阵，shape为$\text{Dictionary Size} \times \text{Word Vector Size}$, 即词语总数量乘以词的维数。注意trainable=False，我们不需要训练词向量，使用预训练好的Glove词向量，并借助Tensorflow自带的embedding_lookup来查找词向量。
  
  这里直接查询到每个batch每个句子中不同单词的词向量。pretrained_embeddings的最后一维就是词向量的维数，因此pretrained_embeddings是3维的（$\text{Batch} \times \text{Sequence} \times \text{Observation} $）。

字符向量：

将单词看成序列，序列由字符构成，字符看成序列不同时刻的观测输入。

下面同样针对的是1个batch，因此第一维都设置成batch。

为不同时刻的观测输入设置id，这里也就是为每个字符设置一个id。目的是查找观测的向量化表示。
1
2
# shape = (batch size, max length of sentence, max length of word)
char_ids = tf.placeholder(tf.int32, shape=[None, None, None])
这里也是针对1个batch，查询不同句子不同单词不同字符的词向量。因此是三维的。$\text{Batch Size} \times \text{Sentence Length} \times \text{Word Length}$。Batch Size是这个Batch中句子的数量，Sentence Length是句子的最大长度，Word Length是单词的最大长度。
为不同序列设置有效长度，这里的单词看做序列，因此也就是每个单词的字符数目。目的是记录batch不同序列的长度。
1
2
# shape = (batch_size, max_length of sentence)
word_lengths = tf.placeholder(tf.int32, shape=[None, None])
同样针对batch，记录不同句子的不同单词的有效长度。word_lengths二维数组shape为$\text{Batch Size} \times \text{Sentence Length}$，每个元素记录了单词(序列)的有效长度。将该二维数组reshape成一维后，就记录的是Batch中所有单词(序列)的有效长度。

查询字符向量

K = tf.get_variable(name="char_embeddings", dtype=tf.float32,
    shape=[nchars, dim_char])
    
# shape = (batch size, sentence, word, dim of char embeddings)
char_embeddings = tf.nn.embedding_lookup(K, char_ids)

K是字符向量矩阵，是需要进行学习的，shape为$\text{Char Dictionary Size} \times \text{Char Vector Size}$。$\text{Char Dictionary Size}$是所有的字符总数目，$\text{Char Vector Size}$是每个字符向量的维度。char_embeddings最后一维代表的就是字符的向量维数。另外，char_embeddings是四维的，$\text{Batch} \times \text{Sentence Length} \times \text{Word Length} \times \text{Char Vector Size}$。这个稍后需要reshape成3维才能适配LSTM接口。实际上前两维可以合并，因为此处我们的序列是单词，不同句子单词一视同仁，直接拼接在一起就行。

Bi-LSTM提取字符特征

# 1. get character embeddings
K = tf.get_variable(name="char_embeddings", dtype=tf.float32,
    shape=[nchars, dim_char]) 
# shape = (batch size, sentence, word, dim of char embeddings)
char_embeddings = tf.nn.embedding_lookup(K, char_ids)

# 2. put the time dimension on axis=1 for dynamic_rnn
s = tf.shape(char_embeddings) # store old shape
# shape = (batch x sentence, word, dim of char embeddings)
char_embeddings = tf.reshape(char_embeddings, shape=[-1, s[-2], s[-1]])
word_lengths = tf.reshape(self.word_lengths, shape=[-1])

# 3. bi lstm on chars
cell_fw = tf.contrib.rnn.LSTMCell(char_hidden_size, state_is_tuple=True)
cell_bw = tf.contrib.rnn.LSTMCell(char_hidden_size, state_is_tuple=True)

_, ((_, output_fw), (_, output_bw)) = tf.nn.bidirectional_dynamic_rnn(cell_fw,
    cell_bw, char_embeddings, sequence_length=word_lengths,
    dtype=tf.float32)
    
# 4. concat to form final word embedding
# shape = (batch x sentence, 2 x char_hidden_size)
output = tf.concat([output_fw, output_bw], axis=-1)

# shape = (batch, sentence, 2 x char_hidden_size)
char_rep = tf.reshape(output, shape=[-1, s[1], 2*char_hidden_size])

# shape = (batch, sentence, 2 x char_hidden_size + word_vector_size)
word_embeddings = tf.concat([pretrained_embeddings, char_rep], axis=-1)

第一步获取字符的词向量，注意char_embeddings维度是4维。
第二步，我们的输入序列是单个word的字符序列，因此不同句子不同单词不需要区分，直接连接起来，并指定不同序列的长度即可，即word的长度。一定要注意，我们此处的序列是单词！

这一步也是为了使用LSTM接口，将char_embeddings的reshape一下，前2维合并，即batch_size中句子、句子中单词2个维度摊平，也就是相当于把batch中所有的句子拼接起来，相应的word_lengths也修改，修改后的word_lengths一维数组每个元素记录了每个单词序列的长度，也就是LSTM需要建模的每条序列的长度。这样，word_lengths就能够把不同序列区分开。
第三步，前面得到了适配LSTM接口的3维数组，即$\text{Batch} \times \text{Sequence} \times \text {Observation}$。此处先构建前向LSTM单元和后向LSTM单元，并指定隐藏层单元的大小。接着将LSTM组件作为bidirectional dynamic rnn的参数传入（此处也可以使用GRU组件）。另外，注意此处要传入sequence_length参数，代表每个序列(单词)的有效长度。这个参数的作用是使得神经网络能够建模不同长度的序列样本。因为前面我们得到的第二维Senquence Length是最大单词序列的长度，但不同单词长度不一样，使用该参数能够让LSTM知道每个单词序列的有效长度，当隐藏神经元到达每个单词序列的有效长度处时，就停止继续前向传播，输出最后一个时刻的隐藏单元向量。如果不指定该参数，就默认每个序列长度一样了。bidirectional_dynamic_rnn返回值第一个参数是前向和后向序列上每个时刻的隐藏层单元输出，此处不需要；第二个参数是前向和后向最后1个时刻的状态输出。因为我们的LSTM指定了state_is_tuple=True,因此这个状态包含了记忆单元$\mathbf c$值以及隐藏层单元$\mathbf h$值。因此需要对上述第二个参数继续拆包，得到最后1个时刻的隐藏层单元$\mathbf h$值。这是我们需要的。这个作为整个单词序列提取到的字符特征，因此是1个单词对应1个字符特征。
第四步，拼接得到的字符向量和预训练好的单词向量，得到最终每个单词的向量化表示。首先将前向和后向得到的单词的字符级特征拼接在一起，axis=-1代表按照最后一维来拼接，拼接后得到的output的shape为 $(\text{batch * sentence}) \times (\text{2 * char_hidden_size})$。再reshape一下，变成$\text{batch} \times \text{sentence } \times (\text {2 * char_hidden_size})$。第二维每个句子的长度需要使用前面保存的参数s[1]。最后和pretrained_embeddings拼接起来。得到最终的，$\text{batch} \times \text{sentence} \times \text{observation}$。observation的维度数为$\text{word_vector_size} + (2 * \text{char_hidden_size})$。

提取了不同句子序列中不同单词的特征word_embeddings，接下来需要使用Bi-LSTM来建模句子序列，来提取句子上下文级别的特征（回顾一下，前面我们借助Bi-LSTM提取了单词级别的特征），句子每个时刻上下文级别的特征将作为CRF的输入特征（观测特征），并结合每个时刻的标签，来进行命名实体识别。

上下文词语特征表示

前面得到了单个词语的特征，此处将使用Bi-LSTM运行句子单词序列，来提取每个单词的上下文特征表示，并作为每个时刻的隐藏单元输出。示意图如下：

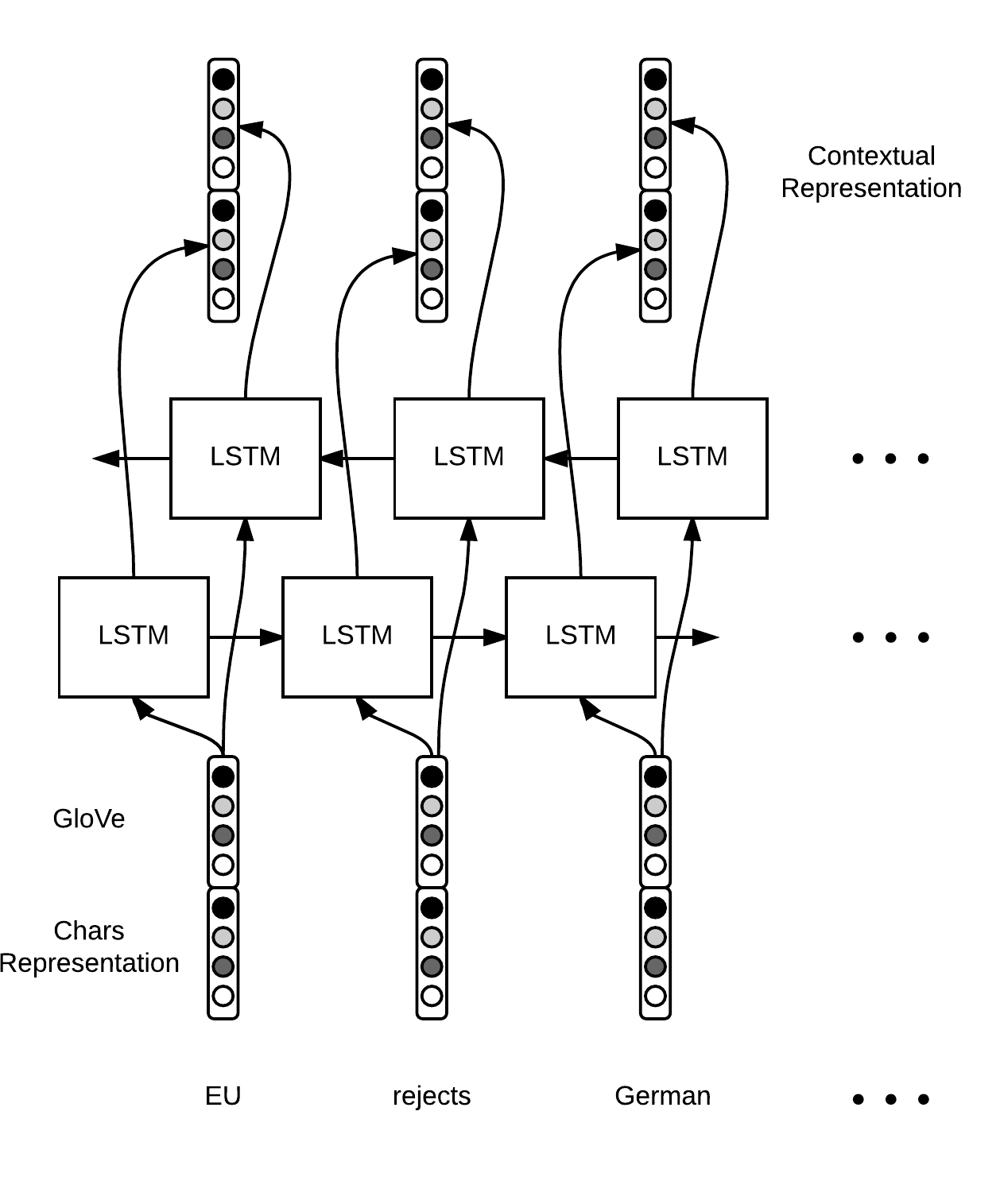
上述示意图以句子序列：EU rejuects German…作为输入。每个时刻的单词都会得到1个前向隐向量表示和1个后向隐向量表示，拼接起来作为该时刻的单词的上下文特征表示。此处我们需要保留每个时刻的特征，而不仅仅是最后一个时刻的特征。

cell_fw = tf.contrib.rnn.LSTMCell(hidden_size)
cell_bw = tf.contrib.rnn.LSTMCell(hidden_size)

(output_fw, output_bw), _ = tf.nn.bidirectional_dynamic_rnn(cell_fw,
    cell_bw, word_embeddings, sequence_length=sequence_lengths,
    dtype=tf.float32)

context_rep = tf.concat([output_fw, output_bw], axis=-1)

也就是说，我们要用的是bidirectional_dynamic_rnn返回值的第一个值。注意bidirectional_dynamic_rnn的输入是word_embeddings，shape为$\text{Batch} \times \text{Sentence} \times \text{Word}$。即输入序列是$m$个$n$维词向量，$w_1,w_2,…,w_m \in \mathbb{R}^n$，输出序列为$m$个$k$维上下文向量，$h_1,h_2,…,h_m \in \mathbb{R}^k$。$w_t$只捕捉了词语级别的特征（句法+语义），而$h_t$还捕捉了上下文特征。 context_rep维度为$\text{Batch} \times \text{Sentence} \times \text{2*hidden_size}$。因为我们传入了sequence_length，因此context_rep中无效的时间步对应的上下文特征使用0来填充。

解码

此步骤将利用上述词语的特征，来解码词语的命名实体类型。前面我们提取了词语的特征$h_t$, $h_t$涵盖了词语的语义特征(Glove)、字符级特征（Bi-LSTM）以及上下文特征（Bi-LSTM）。此处将使用一个全连接层，得到一个输出向量，向量的每个分量代表不同命名实体的得分。

我们一共有9个类别，B-PER、I-PER、B-LOC、I-LOC、B-ORG、I-ORG、B-MISC、I-MISC、O。令矩阵$W\in\mathbb{R}^{9 \times k}$,偏置$b \in \mathbb{R}^{9}$, 全连接层计算一个前向传播输出向量$s\in \mathbb{R}^{9} = W \cdot h + b$。$s$的第$i$个分量$s[i]$解释为该单词属于类别$i$的得分。

W = tf.get_variable("W", shape=[2*self.config.hidden_size, self.config.ntags],
                dtype=tf.float32)

b = tf.get_variable("b", shape=[self.config.ntags], dtype=tf.float32,
                initializer=tf.zeros_initializer())

ntime_steps = tf.shape(context_rep)[1]
context_rep_flat = tf.reshape(context_rep, [-1, 2*hidden_size])
pred = tf.matmul(context_rep_flat, W) + b
scores = tf.reshape(pred, [-1, ntime_steps, ntags])

将context_rep展平，每个时刻隐向量$h$看成1个输入样本。最后再reshape成$\text{Batch} \times \text{Sentence} \times \text{Tag}$。注意这里每个无效的时间步也进行了计算，后面解码的时候需要把这些无效时间步剔除掉即可。

接下来要根据得分预测命名实体的类别。

有2种方式来预测，1是使用softmax激活函数，直接输出每个时刻词语类别的概率分布。2是使用Linear-CRF来计算每个时刻词语类别的概率分布。第一种方法仍然只利用了局部的信息，即使捕捉了上下文特征。第二种方法会利用到邻近的词语的标签决策。比如对于New York实体，New实体的识别对York的识别有很大的作用。给定一个句子词语序列$w_1,w_2,…,w_m$，以及对应的得分向量序列$\mathbf s_1,\mathbf s_2,…, \mathbf s_m$和标签序列$y_1,y_2,…,y_m$，linear-chain CRF定义的全局得分$C \in \mathbb{R}$如下：
$$
\begin{align}
C(y_1, \ldots, y_m) &= \mathbf b[y_1] &+ \sum_{t=1}^{m} \mathbf s_t [y_t] &+ \sum_{t=1}^{m-1} \mathbf T[y_{t}, y_{t+1}] &+ \mathbf e[y_m]\\
&= \text{begin} &+ \text{scores} &+ \text{transitions} &+ \text{end}
\end{align}>
$$
$T \in \mathbb{R}^{9\times 9}$是转移矩阵，用于捕捉标签决策之间的线性依赖。$e、b$是得分向量，用于捕捉起始标签和终止标签代价。也就是说$C$定义了一个标签序列的得分。$\mathbf s_t$为全连接层输出的单词$w_t$的标签向量得分。

目标是找到$C$最大的一个标签序列$y_1,y_2,…,y_m$.

示例如下：Pierre loves Pairs。假定只有3种实体类型PER、O、LOC。${y_1,y_2,y_3}$的其中两种路径如下：

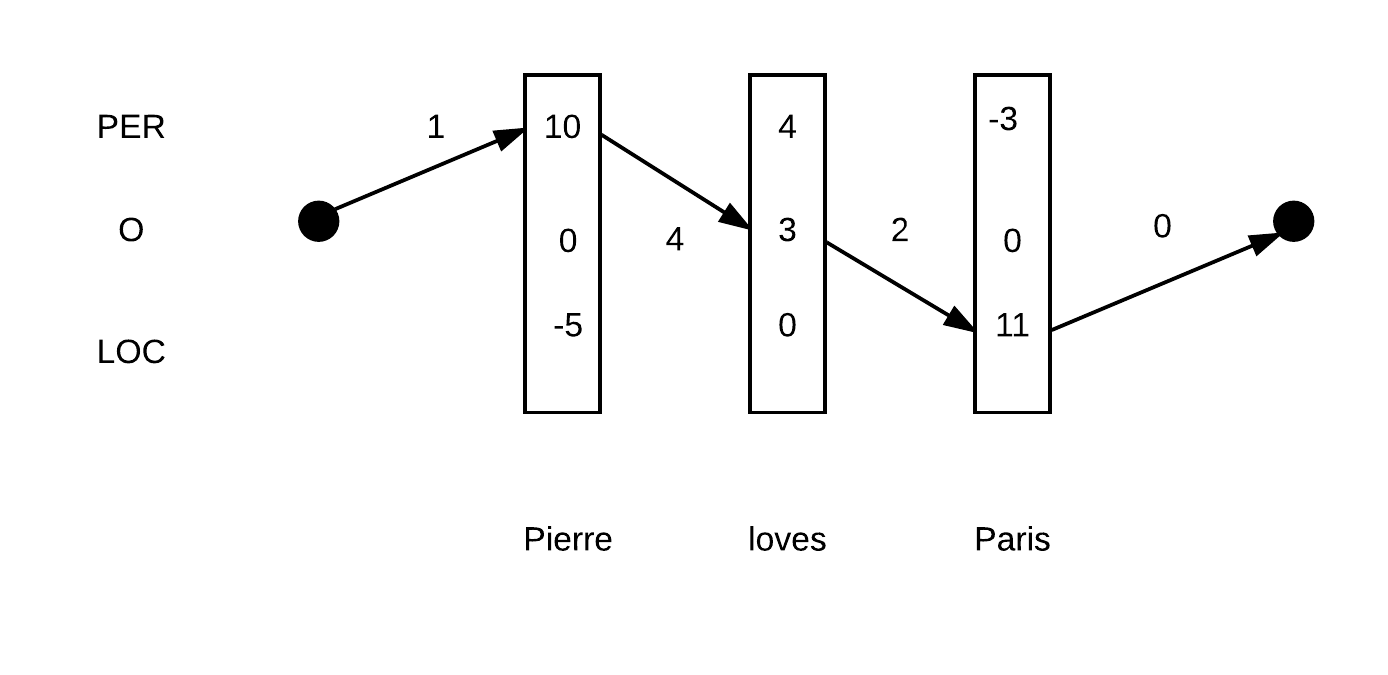
上图代表的路径：PER-O-LOC得分为：$ 1 + (10 +3+11) + (4 + 2) + 0= 31$

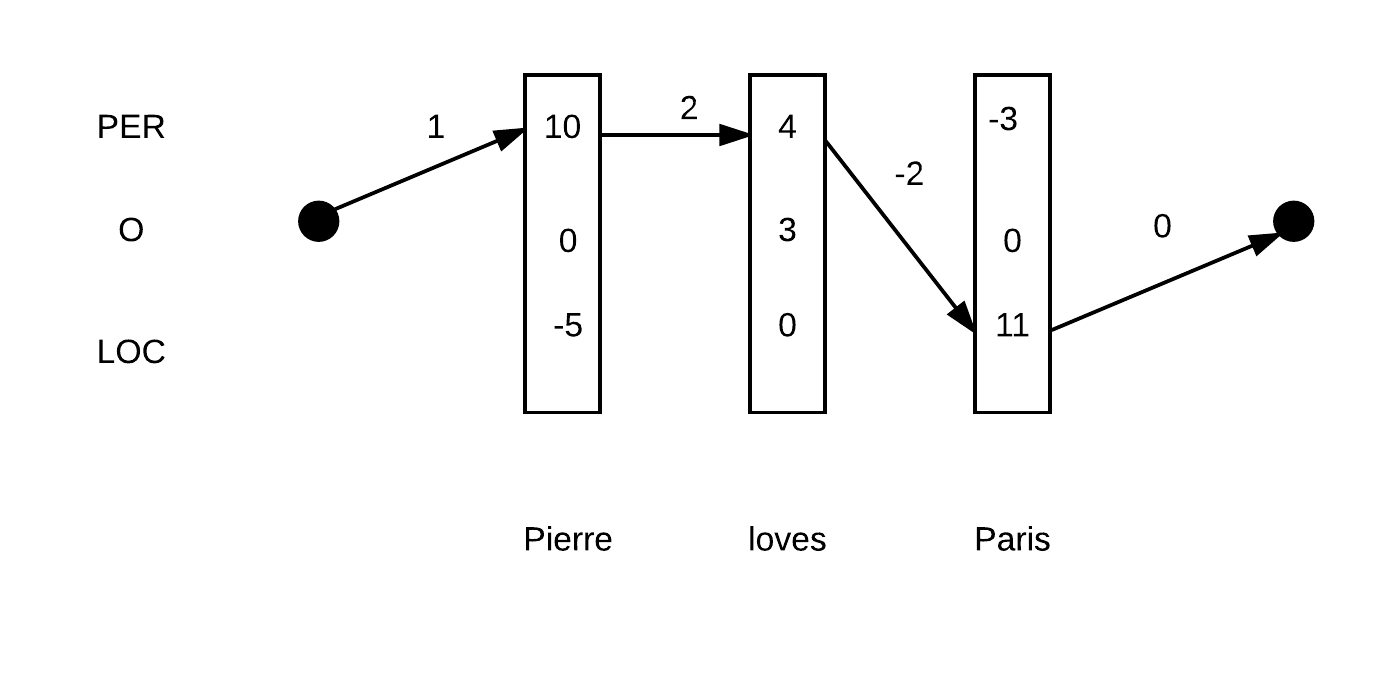
上图代表的路径：PER-PER-LOC得分为：$ 1+(10+4+11) + (2-2) + 0 = 26$

因此根据Linear-chain CRF的话，图1的序列得分更高。如果直接根据每个单词各自局部的得分最高项来决策的话，那么最终决策为PER-PER-LOC，即图2。显然没有图1好。

问题关键是如何找到最优的序列。除此之外，我们还需要计算所有序列的概率分布，这样才能使用CRF的训练方法进行优化。

查找最优序列

蛮力搜索的的话，对于一个长度为$m$的句子，标签序列共$9^m$种，穷举计算显然不可行。可以采取动态规划来解决。假设对于从时间步$y^{t+1}$开始、$y^{t+1}$取9种可能的值的每种序列$t+1,…,m$，已经得到最优的解$\tilde{s}_{t+1}(y^{t+1})$。那么：对于$t,…,m$时间步，某个$y^t$(共9种)的最优解$\tilde{s}_t(y^t)$满足：
$$
\tilde{s}_t(y_t) = arg max_{y_t,…,y_m}C(y_t,…,y_m) \\
= argmax_{y_{t+1}} s_t[y_t] + T[y_t,y_{t+1}] + \tilde{s}_{t+1}(y^{t+1})
$$
上述为动态规划状态转移方程。因此，对于每个时间步，需要按照上述计算该时间步9种标签的最大值，argmax复杂度$O(9)$，因此单个时间步复杂度为$O(9 \times 9)$。m个时间步复杂度为$O(9 \times 9 \times m)$。

计算序列概率值

计算序列的概率值，只需要在所有序列的得分上使用softmax即可。softmax分母需要计算配分函数，
$$
Z = \sum_{y_1, \ldots, y_m} e^{C(y_1, \ldots, y_m)}
$$
则：
$$
\mathbb{P}(y_1,…,y_m)=\frac{e^{C(y_1,…,y_m)}}{Z}
$$
另外，$Z$也具有动态规划状态转移方程。令，$Z_t(y_t)$是时间步t标签为$y_t$开始的所有序列的得分和。则：
$$
\begin{align}
Z_t(y_t) &=\sum_{y_{t+1},…,y_{m}} e^{s_t[y_t] + T[y_{t}, y_{t+1}]+C(y_{t+1},…,y_m)} \\
&= \sum_{y_{t+1}} e^{s_t[y_t] + T[y_{t}, y_{t+1}]} \sum_{y_{t+2}, \ldots, y_m} e^{C(y_{t+1}, \ldots, y_m)} \\
&= \sum_{y_{t+1}} e^{s_t[y_t] + T[y_{t}, y_{t+1}]} Z_{t+1}(y_{t+1})\\
\log Z_t(y_t) &= \log \sum_{y_{t+1}} e^{s_t [y_t] + T[y_{t}, y_{t+1}] + \log Z_{t+1}(y_{t+1})}
\end{align}
$$

训练

使用交叉熵损失训练：
$$
log (\mathbb{P} (\tilde{y}))
$$
$\tilde{y}$是真实的标注序列，其中：
$$
\mathbb{P}(\tilde{y}) = \frac{e^{C(\tilde{y})}}{Z}
$$
可以使用开源CRF损失实现：

# shape = (batch, sentence)
labels = tf.placeholder(tf.int32, shape=[None, None], name="labels")

log_likelihood, transition_params = tf.contrib.crf.crf_log_likelihood(
scores, labels, sequence_lengths)

loss = tf.reduce_mean(-log_likelihood)

labels记录了每个句子每个单词的真实标注。scores是神经网络全连接层的输出。crf_log_likelihood会自动计算$C(\tilde{y})$。具体公式可能与上述有些出路。