本篇文章主要介绍图表示学习在推荐系统中常见的user-item interaction数据上的建模。我们可以将user-item interaction data看做是关于user-item的二分图Bipartite,这样可以基于GNN的方法进行user和item embedding的学习。主要介绍三篇顶会文章,如下:
- KDD2018,GCMC:Graph Convolutional Matrix Completion,在movie-len上的state of the art模型。
- SIGIR2019,NGCF:Neural Graph Collaborative Filtering,首次提出图协同过滤的概念。
- MM2019,MMGCN:MMGCN: Multi-modal Graph Convolution Network for
Personalized Recommendation of Micro-video,多模态图卷积神经网络。
GCMC
KDD2018: Graph Convolutional Matrix Completion
Introduction
这是一篇发表在KDD2018(二作T.N.Kipf是著名的 GCN 的一作)的文章。将矩阵补全问题看做是关于user-item 二分图的链接预测问题(a bipartite user-item graph with labeled edges),每种链接边可以看做是一种label(例如多种交互行为:点击,收藏,喜欢,下载等;在评分中,1~5分可以分别看做一种label)。有点像multi-view bipartite graph。作者提出了一个信息传递(differentiable message passing)的概念,通过在bipartite interaction graph上进行信息传递来学习结点的嵌入,再通过一个bilinear decoder进行链接预测。
Formulation
给定关于用户-物品交互数据的二分图,$G=(\mathcal{W}, \mathcal{E}, \mathcal{R})$,其中$\mathcal{W}$是结点,包括用户结点$u_i \in \mathcal{W}_u, i=\{1,…,N_u\}$和物品结点$v_j \in \mathcal{W}_v, j=\{1,…,N_v\}$,$\mathcal{W}=\mathcal{W}_u \cup \mathcal{W}_v$. 边$(u_i ,r,v_j ) \in \mathcal{E}$代表了用户$u_i$和$v_j$的交互行为类型为$r$,$r \in \mathcal{R}=\{1,…,R\}$.其中$R$是总的交互类型种数。这里的交互行为原文中使用的是评分level来代表,如1~5分,则代表5种rating level,即:$R=5$。
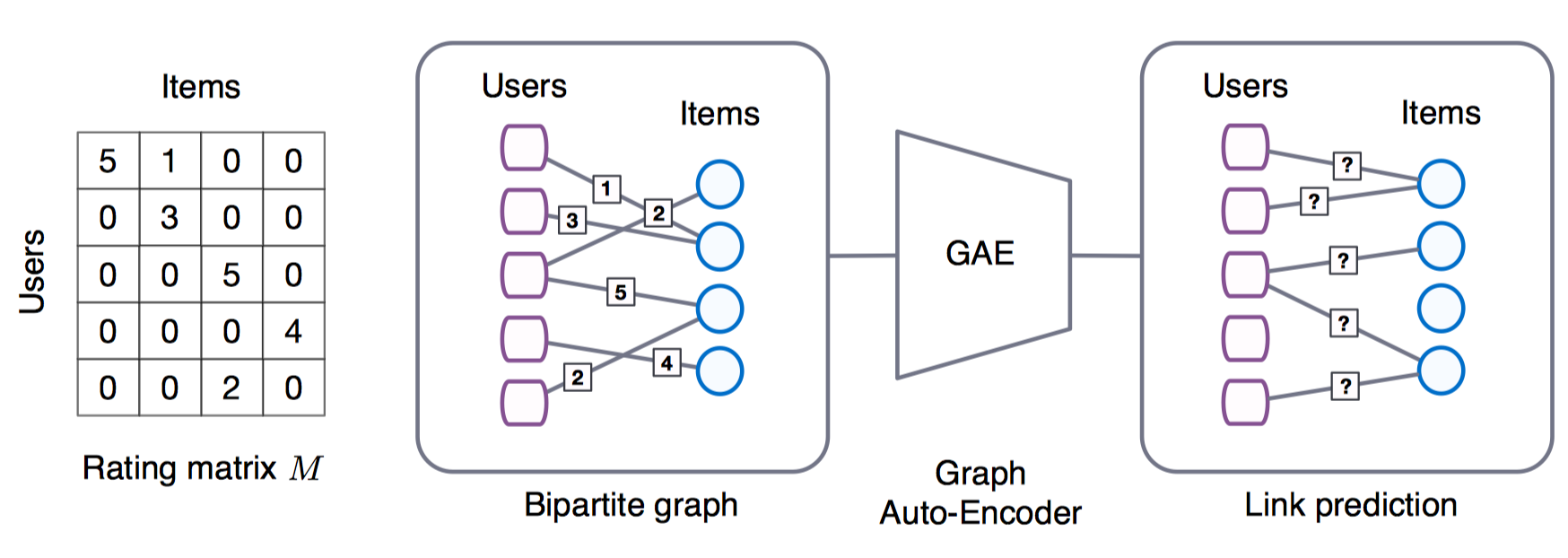
可以看做是一个graph auto-encoders。Graph Encoder Model形如:$[Z_u ,Z_v ] = f (X_u ,X_v , M_1 , . . . , M_R)$。其中,$X_u, X_v$是用户或物品的Feature矩阵。$M_r \in {0, 1}^{N_u \times N_v}$是和交互类型$r$相关的邻接矩阵。$Z_u, Z_v$是输出的结点嵌入。Decoder形如:$\hat{M} = (Z_u ,Z_v)$用于预测$u$和$v$的链接类型或评分矩阵的评分值。然后使用重构误差最小化来训练模型,如RMSE或交叉熵。
Models
Graph convolutional encoder
作者首先提出了一种针对不同rating level的sub-graph分别进行局部图卷积,再进行汇聚的encoder模型。这种局部图卷积可以看做是一种信息传递(message passing),即:向量化形式的message在图中不同的边上进行传递和转换。每种边特定的信息传递过程如下(edge-type specific message),以item $j$ 传递到 user $i$为例:
$$
\mu_{j \rightarrow i, r}= \frac{1}{c_{ij}} W_r x_j^v \tag{1}
$$
其中,$c_{ij}$是归一化常数因子,如$|\mathcal{N}(u_i)|$或$\sqrt{|\mathcal{N}(u_i) \mathcal{N}(v_j)|}$。$W_r$是 edge-type specific parameter matrix。$x_j^v$是item $j$初始的特征,作者采用的是unique one-hot vector作为特征。相当于把$x_j^v$这一信息传递到了用户结点$i$上。这样针对每种类型的边,可以把所有$i$的邻域节点传递过来的信息做个累加操作,$\sum_{j \in \mathcal{N}_r(u_i)}{\mu_{j \rightarrow i, r}}$, $\text{for } r = 1,2,…,R$.
接着需要将不同edge-type采集到的信息进行一个汇聚,
$$
h_i^v = \sigma \left[\text{accum}\left(\sum_{j \in \mathcal{N}_1(u_i)}{\mu_{j \rightarrow i, 1}},…,\sum_{j \in \mathcal{N}_r(u_i)}{\mu_{j \rightarrow i , r}},…, \sum_{j \in \mathcal{N}_R(u_i)}{\mu_{j \rightarrow i, R}}\right)\right] \tag{2}
$$
上式的$\text{accum}$是一个汇聚操作,例如可以采用连接操作或求和操作,$\sigma$ 是激活函数,例如Relu。 完整的式(2)称为
graph convolution layer,可以叠加多个graph convolution layer。
为了得到用户$u_i$最终的embedding,作者加了个全连接层做了个变换:
$$
z_{i}^u = \sigma(W h_i^u) \tag{3}
$$
物品$v_i$的embedding和用户$u_i$的求解是对称的,只不过使用的是两套参数。
作为拓展,值得一提的是,很多人忽略了归一化因子$c_{ij}$的重要性。一种观点是随着GCN层数的叠加,$c_{ij}$起着embedding平滑的作用(Embedding Smoothness)。我们以二层GCN为例,从协同过滤角度来阐述这一归一化因子的重要性(源自另一篇文章的观点LightGCN)。此处忽略多视图$r$以及非线性$\sigma$。令,$c_{ij}=\sqrt{|\mathcal{N}(u_i) \mathcal{N}(v_j)|}$为例,记$\boldsymbol{e}_j^{(1)}=W x_j^v$,当$x_j$为id one-hot vector时,可以认为就是item的嵌入;user同理。
根据式子2,neighbor aggregation操作。我们观察用户$u, v$是如何产生协同过滤效果的。
$$
\begin{aligned}
\boldsymbol{e}_u^{(2)} &= \sum_{j \in \mathcal{N}_u} \frac{1}{\sqrt{|\mathcal{N}_u| \cdot |\mathcal{N}_j}|} \boldsymbol{e}_j^{(1)}= \sum_{j \in \mathcal{N}_u} \frac{1}{\sqrt{|\mathcal{N}_u| \cdot |\mathcal{N}_j}|} (\sum_{v \in \mathcal{N}_j} \frac{1}{\sqrt{|\mathcal{N}_j| \cdot |\mathcal{N}_v|}}\boldsymbol{e}_v^{(0)}) \\
&=\sum_{j \in \mathcal{N_u}} \frac{1}{|\mathcal{N}_j|} \sum_{v \in \mathcal{N}_j} \frac{1}{\sqrt{|\mathcal{N}_u| \cdot |\mathcal{N}_v|}} \boldsymbol{e}_v^{(0)}
\end{aligned}
$$
可以看出如果$u$和$v$存在共同交互过的item $j$ (从公式看,$j$是$u$的邻居,$v$是$j$的邻居,故$j$ 是$u, v$的co-interacted item),则$v$对$u$的平滑强度可以使用下述系数来表示 (the smoothness strength of v on u is measured by the coefficient),
$$
c_{v \rightarrow u} = \frac{1}{\sqrt{|\mathcal{N}_u| \cdot |\mathcal{N}_v|}} \sum_{j \in \mathcal{N}_u \cap \mathcal{N}_v} \frac{1}{|\mathcal{N}_j|}
$$
非co-interacted items对上式不起作用,故可以直接去掉,重新整理得到该系数。这个系数具备很强的可解释性,可以从协同过滤角度来阐述second-order的近邻$v$对$u$嵌入表示的影响。
- co-interacted items越多,则$v$对$u$的协同影响越大,对应系数中的求和项。co-interacted items沟通了$u,v$,显然越多,协同影响的越大。
- co-interacted items本身越不流行,则$v$对$u$的影响越大,对应$1/|\mathcal{N}_j|$项。越不流行的items富含的信息量越大。一个item很不流行,而$u,v$却都交互过,那这个item产生的协同影响效果显然越大越好。
- $v$的交互行为越稀少,则$v$对$u$的影响越大,对应求和前的$1/\sqrt{|\mathcal{N}_v|}$。越不活跃的users提供的协同信号越重要。$u$和一个很不活跃的用户$v$共同交互过某个item,显然这个是很少见的情况,$v$能提供更多的协同信号。
上述系数从衡量user similarity的协同过滤角度提供了完美的可解释性。
Bilinear decoder
为了重构二分图上的链接,作者采用了bilinear decoder,把不同的rating level分别看做一个类别。bilinear operation后跟一个softmax输出每种类别的概率:
$$
p(\hat{M}_{ij}=r)=\text{softmax}((z_i^u)^T Q_r z_j^v) \tag{4}
$$
$Q_r$是可训练的edge-type r特定的参数。
则最终预测的评分是关于上述概率分布的期望:
$$
\hat{M_{ij}} = g(u_i ,v_j) = E_{p(\hat{M}_{ij}=r)}[r] = r p(\hat{M}_{ij}= r) \tag{5}
$$
Model Training
最小化 negative log likelihood of the predicted ratings $\hat{M}_{ij}$.
$$
\mathcal{L} = − \sum_{i,j;Ω_{ij}=1} \sum_{r=1}^R I[M_{ij}=r] \log p(\hat{M}_{ij}=r) \tag{6}
$$
作者在训练过程中,还使用了一些特殊的优化点。
Node dropout
对特定的某个节点,随机地将outgoing的信息随机drop掉。这能够有效的提高模型的鲁棒性。例如:去除掉某个结点时,模型性能不会有太大的变化。
Weight sharing
不是所有的用户或物品在不同rating level上都拥有相等的评分数量。这会导致在局部卷积时,$W_r$上某些列可能会比其他列更少地被优化。因此需要使用某种在不同的$r$之间进行参数共享的方法。
$$
W_r = \sum_{s=1}^r T_s \tag{7}
$$
$T_s$是基础矩阵。也就是说越高评分,$W_r$包含的$T_s$数量越多。
作者采用了一种基于基础参数矩阵的线性组合的参数共享方法:
$$
Q_r = \sum_{s=1}^{n_b} a_{rs} P_s \tag{8}
$$
其中,$n_b$是基础权重矩阵的个数,$P_s$是基础权重矩阵。$a_{rs}$是可学习的系数。
Side Information
为了建模结点的辅助信息,作者在对$h_i^u$做全连接层变换时,考虑了结点的辅助信息:
$$
z_{i}^u = \sigma(W h^u_i +W_2^{u,f} f_i^u), f_i^u = σ(W_1^{u,f} x_i^{u,f} + b^u) \tag{9}
$$
即:先对特征$x_i^{u,f}$做一个变换得到$f_i^u$。与$h^u_i$分别经过线性变换后加起来并激活,最终得到结点的嵌入表示。
Summary
总结一下整体的过程,模型的核心过程形式化如下:
$$
\boldsymbol{z}_i^u, \boldsymbol{z}_j^v = \text{GNN-Encoder}(\mathcal{G}_{u,i}) \tag{10}
$$
$$
p(\hat{M}_{ij}=r)= \text{softmax}\left(\text{Bilinear-Decoder}(\boldsymbol{z}_i^u, \boldsymbol{z}_j^v)\right) \tag{11}
$$
$$
\mathcal{L} = − \sum_{i,j;Ω_{ij}=1} \sum_{r=1}^R I[M_{ij}=r] \log p(\hat{M}_{ij}=r) \tag{12}
$$
$$
\hat{M_{ij}} = g(u_i ,v_j) = E_{p(\hat{M}_{ij}=r)}[r] = r p(\hat{M}_{ij}= r) \tag{13}
$$
先经过GNN-Encoder输出user和item的嵌入表示(公式10),再经过Bilinear Decoder输出属于不同评分值的概率(公式11),最后公式(12)是关于评分多分类问题的交叉熵损失。具体预测的时候使用公式(13)预测评分,进行topk推荐。
NGCF
SIGIR2019: Neural Graph Collaborative Filtering
Intuition
这是何向南教授团队在SIGIR2019发表的一篇文章,主要针对隐式反馈行为数据。为了解决传统的方法主要通过user或item的pre-existing fetures的映射得到user和item的embedding,而缺乏了user和item之间重要的协同信息(collaborative signal)这一问题,作者提出了一种新的推荐框架——神经图协同过滤。这篇文章核心的目标问题在于如何更好的将user-item之间的协同信息建模到user和item的emebdding表示中。1
2
3
4We develop a new recommendation framework Neural Graph Collaborative Filtering (NGCF),
which exploits the user-item graph structure by propagating embeddings on it.
This leads to the expressive modeling of high-order connectivity in user-item graph,
effectively injecting the collaborative signal into the embedding process in an explicit manner.
传统的方法无法学到很好的Embedding,归咎于缺乏对于重要的协同信息显示地进行编码过程,这个协同信息隐藏在user-item交互数据中,蕴含着users或者items之间的行为相似性。更具体地来说,传统的方法主要是对ID或者属性进行编码得到embedding,再基于user-item interaction定义重构损失函数并进行解码。可以看出,user-item interaction只用到了解码端,而没有用到编码端。这样会导致,学习到的embedding的信息量不够,为了更好的预测,只能依赖于复杂的interaction (decoder) function来弥补次优的embedding在预测上的不足。1
2
3
4
5
6
7The key reason is that the embedding function lacks an explicit encoding of the crucial collaborative signal,
which is latent in user-item interactions to reveal the behavioral similarity between users (or items)
To be more specific, most existing methods build the embedding function with the descriptive features only (e.g., ID and attributes),
without considering the user-item interactions which are only used to define the objective function for model training.
As a result, when the embeddings are insufficient in capturing CF,
the methods have to rely on the interaction function to make up for the deficiency of suboptimal embeddings.
难就难在如何将interaction中的collaboritive signals建模到embedding的表示中。由于原始的interaction数据规模通常比较庞大,使得难以发掘出期望的collaboritive signals(distill the desired collaborative signal)。
作者在这篇文章中提出基于user-item intractions中的high-order connectivity来解决collaboritive signals的发掘和embedding的建模,做法是在user-item interaction graph structure图结构中进行collaborative signal的编码。1
2we tackle the challenge by exploiting the high-order connectivity from useritem interactions,
a natural way that encodes collaborative signal in the interaction graph structure.
关于high-order connectivity含义的可视化如下,$u_1$的两种视角:二分图 和 树
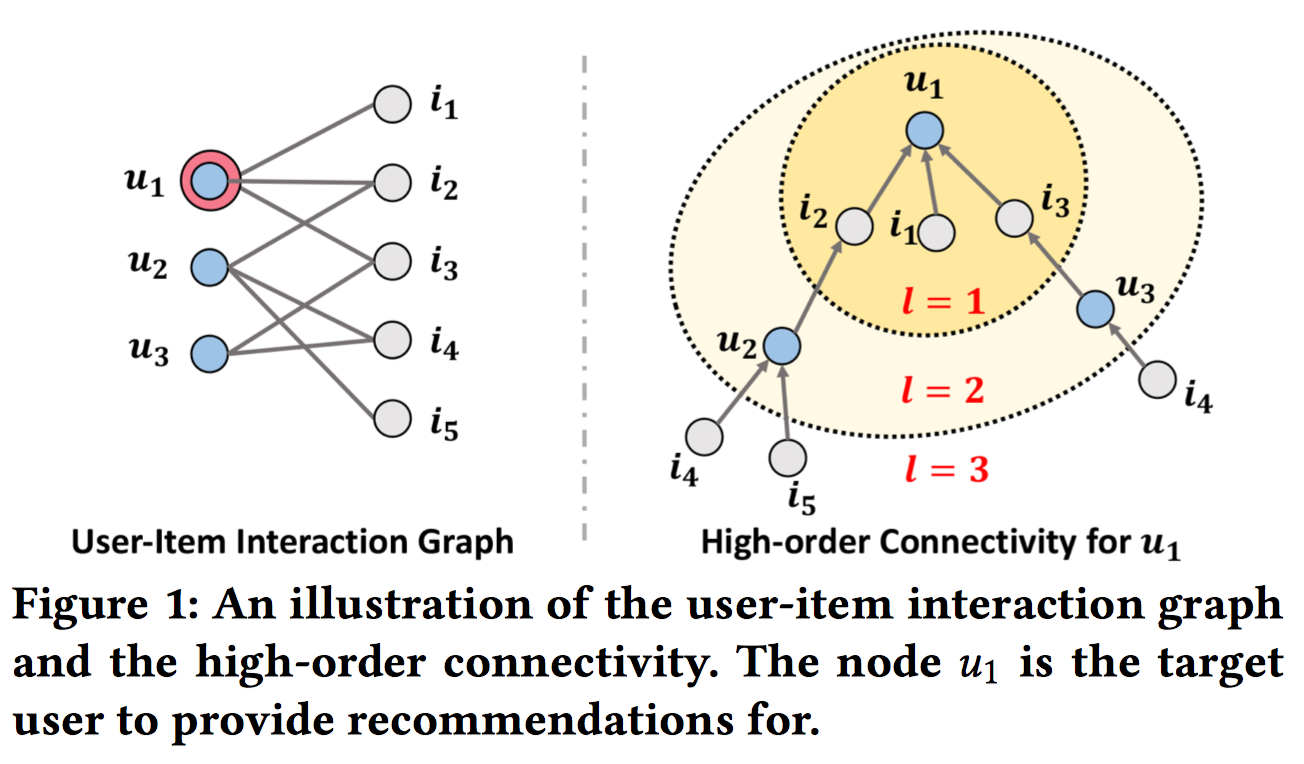
Keys
作者设计了一个神经网络来迭代地在二部图上进行embeddings的传播,这可以看做是在embedding空间构建信息流。1
2We design a neural network method to propagate embeddings recursively on the graph,
which can be seen as constructing information flows in the embedding space.
特别地,作者设计了一种embedding传播层(embedding propagation layer),通过汇聚交互过的items或users来提炼出users或items的embeddings。进一步,通过叠加多个embedding propagation layer,可以使得embeddings来捕获二部图中high-order connectivities所蕴含的协同信息。1
2
3Specifically, we devise an embedding propagation layer, which refines a user’s (or an item’s) embedding
by aggregating the embeddings of the interacted items (or users). By stacking multiple embedding propagation layers,
we can enforce the embeddings to capture the collaborative signal in high-order connectivities.
Models
模型的结构如下:
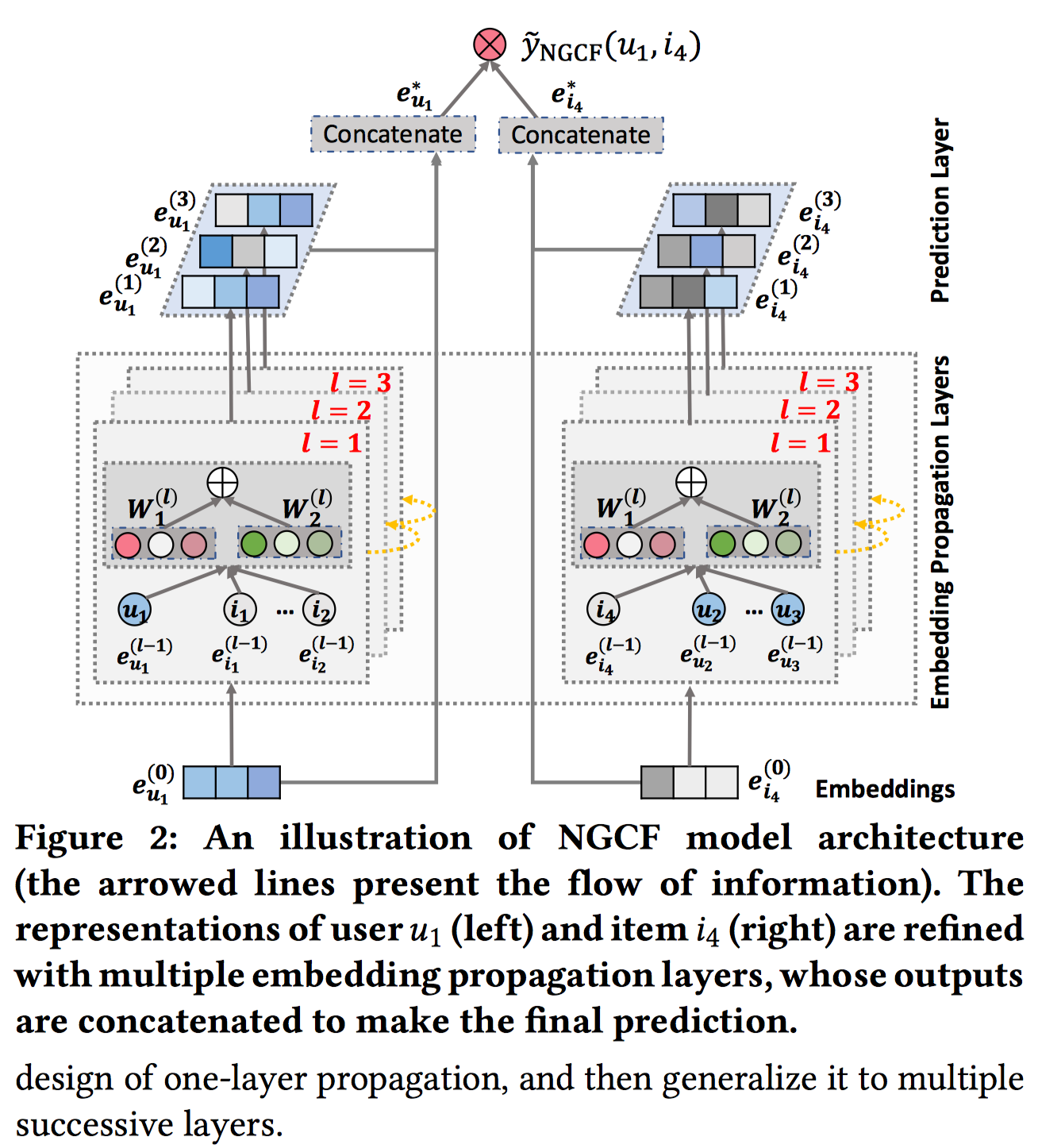
Embedding Layer
嵌入层,offers and initialization of user embeddings and item embeddings。
$$
\boldsymbol{E}=[\boldsymbol{e}_{u1},…,\boldsymbol{e}_{uN} , \boldsymbol{e}_{i1},…,\boldsymbol{e}_{iM}] \tag{1}
$$
传统的方法直接将$E$输入到交互层,进而输出预测值。而NGCF将$E$输入到多层嵌入传播层,通过在二部图上进行嵌入的传播来对嵌入进行精炼。
Embedding Propagation Layer
嵌入传播层,refine the embeddings by injecting high-order connectivity relations。
包括两个步骤,Message construction和Message aggregation。这个部分和KDD2018的GCMC那篇文章是类似的描述方式。
Message Construction
对于每个user-item pair $(u,i)$, 定义从$i$到$u$传递的message如下:
$$
\boldsymbol{m}_{u \leftarrow i}=f(\boldsymbol{e_i}, \boldsymbol{e_u}, p_{ui}) \tag{2}
$$
其中,$\boldsymbol{m}_{u \leftarrow i}$定义为message embedding。$f(\cdot)$是message encoding function,将user和item的 embedding $\boldsymbol{e}_u, \boldsymbol{e}_i$作为输入,并使用$p_{ui}$来控制每条边edge $(u,i)$在每次传播中的衰减系数。
具体的,作者使用如下message encoding function:
$$
\boldsymbol{m}_{u \leftarrow i} = \frac{1}{\sqrt{|\mathcal{N}_u||\mathcal{N}_i|}}(\boldsymbol{W}_1 \boldsymbol{e}_i + \boldsymbol{W}_2(\boldsymbol{e}_i \odot \boldsymbol{e}_u)) \tag{3}
$$
可以看出作者不仅考虑了message的来源$\boldsymbol{e}_i$(传统图卷积方法只考虑这个),还考虑了信息来源和信息目的地之间的关系,即$\boldsymbol{e}_i \odot \boldsymbol{e}_u$,这个element-wise product是典型的特征交互的一种方式,值得学习。$p _u=\frac{1}{\sqrt{|\mathcal{N}_u||\mathcal{N}_i|}}$,$\mathcal{N}_u$是用户$u$的1-hop neighbors。从表示学习角度:$p_{ui}$反映了历史交互item对用户偏好的贡献程度。从信息传递角度,$p_{ui}$可以看做是折扣系数,随着传播路径长度的增大,信息慢慢衰减(这个可以通过叠加多层,并代入到式子,会发现前面系数也是连乘在一起了,说明路径越长,衰减越大)。
Message Aggregation
这个阶段,我们将从用户$u$的邻居传递过来的信息进行汇聚来提炼用户$u$的嵌入表示。
$$
\boldsymbol{e}_u^{(1)} = \text{LeakyReLU}\left(\boldsymbol{m}_{u \leftarrow u} + \sum_{i \in \mathcal{N}_u} \boldsymbol{m}_{u \leftarrow i} \right) \tag{4}
$$
$\boldsymbol{e}_u^{(1)}$是经过一层嵌入传播层得到的提炼后的用户$u$嵌入表示。LeakyReLU允许对于正反馈信息和少部分负反馈信息的编码。$\boldsymbol{m}_{u \leftarrow u} = \boldsymbol{W}_1 \boldsymbol{e}_u$则考虑了self-connection,$\boldsymbol{W}_1$和Equation(2)中的$\boldsymbol{W}_1 $是共享的。
item的嵌入表示同理可得。embedding propagation layer的好处在于显示地挖掘 first-order connectivity信息来联系user和item的表示。
得到的$\boldsymbol{e}_u^{(1)}$可以作为下一个embedding propagation layer的输入,通过叠加多层,可以挖掘multi-hop的关联关系。迭代式如下:
$$
\boldsymbol{e}_u^{(l)} = \text{LeakyReLU}\left(\boldsymbol{m}^{(l)}_{u \leftarrow u} + \sum_{i \in \mathcal{N}_u} \boldsymbol{m}^{(l)}_{u \leftarrow i} \right) \tag{5}
$$
其中,
$$
\boldsymbol{m}^{(l)}_{u \leftarrow i} = p_{u,i}(\boldsymbol{W}^{(l)}_1 \boldsymbol{e}^{(l-1)}_i + \boldsymbol{W}_2^{(l)}(\boldsymbol{e}_i^{(l-1)} \odot \boldsymbol{e}_u^{(l-1)})) \tag{6}
$$
$$
\boldsymbol{m}^{(l)}_{u \leftarrow u} = \boldsymbol{W}^{l}_1 \boldsymbol{e}_u^{(l-1)}
$$
进一步,作者给出了上述Equation(5), (6) 过程的矩阵表示形式,有助于实现layer-wise propagation。
$$
\underbrace{\boldsymbol{E}^{(l)}}_{\mathbb{R}^{(N+M) \times d_l}} = \text{LeakyReLU} \left( \underbrace{(\boldsymbol{\mathcal{L}} + \boldsymbol{I})}_{\mathbb{R}^{(N+M)\times (N+M)}} \overbrace{\boldsymbol{E}^{(l−1)}}^{\mathbb{R}^{(N+M) \times d_{l-1}}} \underbrace{\boldsymbol{W}_1^{(l)}}_{\mathbb{R}^{d_{l-1} \times d_l}} + \boldsymbol{\mathcal{L}} \underbrace{\boldsymbol{E}^{(l−1)}}_{(N+M) \times d_{l-1}} \odot \overbrace{\boldsymbol{E}^{(l−1)}}^{(N+M) \times d_{l-1}} \underbrace{\boldsymbol{W}_2^{(l)}}_{\mathbb{R}^{d_{l-1} \times d_l}} \right) \tag{7}
$$
其中,$E^{(l)} \in \mathbb{R}^{(N +M)×d_l}$,即:把user, item的embeddings矩阵concat在一起,一起进行传播。也就是说,上述是user,item共同进行传播的表示形式,因此所有的矩阵都是concat在一起的形式。
作者说,$\boldsymbol{\mathcal{L}}$表示user-item interaction graph的拉普拉斯矩阵,$\boldsymbol{\mathcal{L}}=\boldsymbol{D}^{-1/2} \boldsymbol{A} \boldsymbol{D}^{-1/2}$,其中,$\boldsymbol{A} \in \mathbb{R}^{(N+M) \times (N+M)}$是邻接矩阵,是user-item 交互矩阵和item-user交互矩阵构成的,即:$\boldsymbol{A} = \left[ \begin{array}{ccc}
\boldsymbol{0} & \boldsymbol{R} \\
\boldsymbol{R}^T & \boldsymbol{0} \\
\end{array} \right] $。(但是我个人记得拉普拉斯矩阵三种方式都不是长这个样子的,有可能这些定义之间差异很小,可能特征根是一样的,故也叫拉普拉斯矩阵吧,虽然和标准的拉普拉斯矩阵之间有一丝差异。本质都是一种graph operator。可参考从 Graph Convolution Networks (GCN) 谈起,讲的非常到位!)
这个矩阵表示形式很好理解,主要点在于,和$\boldsymbol{\mathcal{L}}$的乘法就对应于公式(5)中$\sum_{i \in \mathcal{N}_u} \boldsymbol{m}^{(l)}_{u \leftarrow i}$对邻域节点的汇聚求和操作,其它的一目了然。
Prediction Layer
预测层,aggregates the refined embeddings from different propagation layers and outputs the affinity score of a user-item pair.
最终的嵌入表示是原始的embedding和所有嵌入传播层得到的embedding全部concat在一起的结果。即:
$$
\boldsymbol{e}_u^{*}= \text{concat}(\boldsymbol{e}_u^{(0)},\boldsymbol{e}_u^{(1)},…,\boldsymbol{e}_u^{(L)}) \tag{8}
$$
$\boldsymbol{e}_u^{(0)}$是初始化的embeddings。$\boldsymbol{e}_i^{*}$同理可得。
最后预测user-item交互的时候使用点乘:
$$
\hat{y}_{\text{NGCF}}(u,i) = {\boldsymbol{e}_u^{*}}^T \boldsymbol{e}_i^{*}
$$
Loss
最后作者采用的是pairwise BPR loss进行优化。
$$
Loss = − \sum_{(u,i,j) \in O}\ln \sigma(\hat{y}_{ui} − \hat{y}_{uj}) + \lambda||\Theta||_2^2
$$
其中,$O = \{(u,i, j)|(u,i) \in R^+ , (u, j) \in R^- \}$, $R^+$是观测数据,$R^-$是未观测数据,$\Theta= \{ \boldsymbol{E}, \{ {\boldsymbol{W}_1^{(l)} , \boldsymbol{W}_2^{(l)}\}}_{l=1}^L \}$是所有的可训练参数。
MMGCN
MM2019: MMGCN: Multi-modal Graph Convolution Network for
Personalized Recommendation of Micro-video
Intuition
这篇也是何向南团队(可能是co-author)在顶会ACM Multimedia 2019上发表的文章。为了给内容分享平台提供高质量的推荐,我们不仅要考虑用户和物品的交互 (user-item interactions),还要考虑内容本身多模态的特征 (various modalities (e.g., visual, acoustic, and textual)。目前的多模态推荐方法主要是利用物品本身的多模态内容来丰富item侧的表示;但是很少会利用到users和items之间的信息交互来提升 user侧的表示,进而捕获用户对不同模态特征的细粒度偏好。在这篇文章中,作者主要是想利用user-item interactions来引导每种模态下的表示学习,主要是利用了GNN的message-passing思想,来学习modal-specific representations of users and items。具体而言,作者将user-item interaction graph依据item的多模态特征:图像,文本,语音切分为三个子图,汇聚的时候不仅考虑了邻域的拓扑结构 (可以认为是item id来表征),还考虑了邻域的模态特征 (可以认为是item的feature id来表征)。作者没有将所有的特征一视同仁,而是每个子图对应一种模态特征。
对多模态特征的进行区分对于深入理解用户的preferences有帮助:
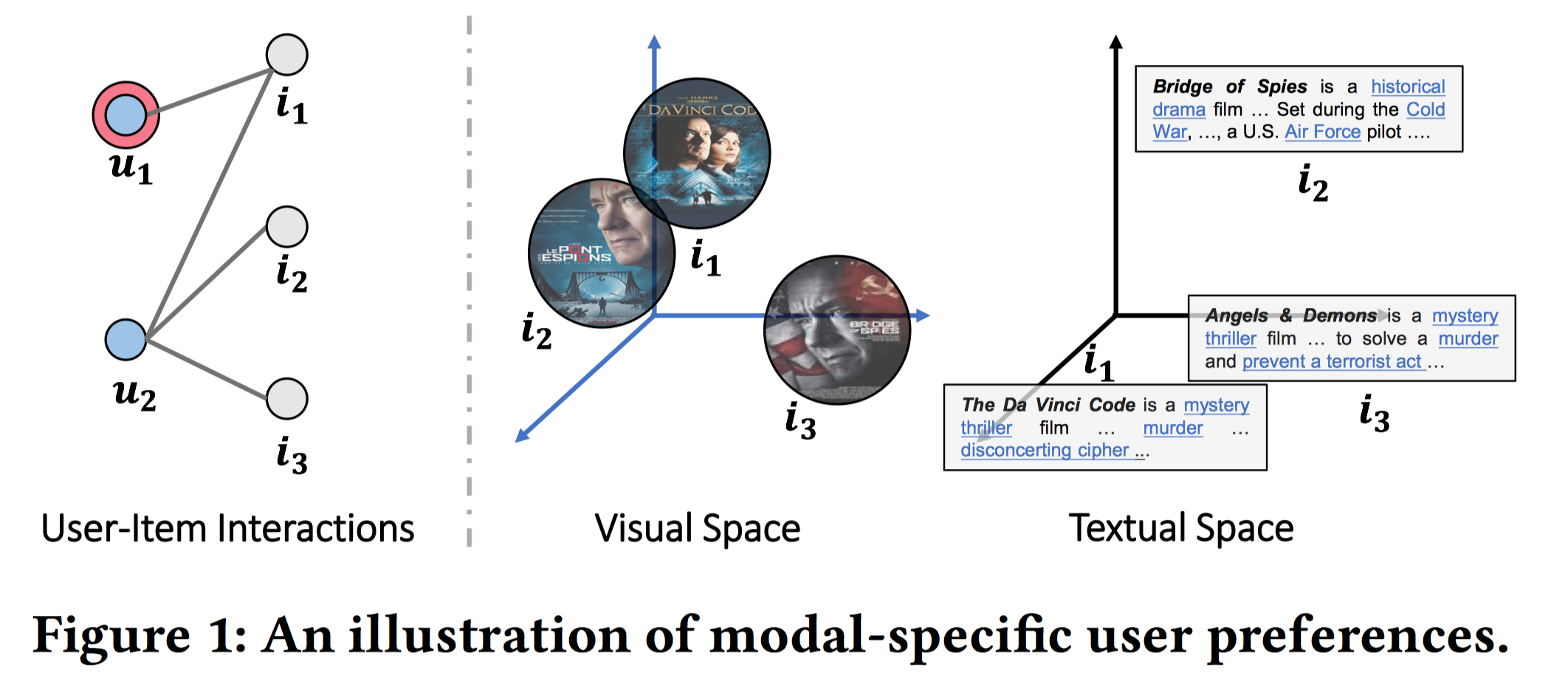
- 不同模态的特征之间存在语义差异。如图1,尽管$i_1$和$i_2$在视觉模态空间很相似,但是在文本模态空间却并不相似,一个是恐怖片、一个是战争片,主题并不一样。如果忽视了这样的模态差异,例如只使用视觉特征的话,会误导item representation。
- 同一个用户对不同模态可能有不同的品味。例如,一个用户可能对视频某些帧的画面感兴趣,但是却对糟糕的视频的背景音乐很失望。
- 不同的模态可以作为不同的角度、途径来发掘用户的兴趣。如图1,如果用户$u_1$更关注视频帧,则$i_2$更适合推荐给他,因为$i_1$和$i_2$在视觉模态更近似;如果$u_1$更关注文字描述,则,$i_3$更适合推荐给他,因为$i_1$和$i_3$在文字模态更近似。
遗憾的是,目前的工作都主要把不同的模态特征作为整体来统一对待 (multimodal features of each item are unified as a single representation, reflecting their content similarity),缺乏对特定模态的用户偏好的建模(modeling of modal-specific user preferences)。
作者希望能够通过关注users和items在不同模态空间下的信息交互 (focus on information interchange between users and items in multiple modalities),借鉴GNN的信息传播机制(information-propagation mechanism)来编码用户和短视频在不同模态下的high-order connectivity,进而捕获特定模态内容下用户的偏好 (user preference on modal-specific contents)。
Keys
为此,作者提出了a Multi-modal Graph Convolution Network (MMGCN),在不同模态下构造user-item二分图(modality-aware bipartite user-item graph)。
- 一方面,从用户角度,用户本身的历史交互行为items能够反映user的个性化兴趣,即从items中聚合特征到user representation是合理的;
- 另一方面,从物品角度,交互过某个item的user group能够追踪物品之间的相似性,因此从users中聚合特征到item presentation也是合理的。
具体而言,MMGCN各自地在不同的模态子图(e.g, visual)下,从交互过的items聚合相应的模态特征(e.g., frames)到user representation,同时利用user group来提升item representation。也就是说不同模态的aggregation操作是每个子图分开单独进行的。然后每个子图下,都会有个combination操作来combine不同模态下的user和item representation,也就是说每个子图下的combined representation都融合了所有模态的特征,combined representation又会作为该子图的下一个GNN aggregation层的输入,然后继续进行combination。总之,aggregation和combination操作迭代执行多次,就能捕获user和item之间多跳的邻居信息。最终,预测的时候可以分别concat user和item在所有子图下的representation,并计算concat后的user和item的representations之间相似性,并进行推荐。
Models
作者不是把所有模态的信息作为整体来统一对待,而是每种模态进行区分对待。首先基于user-item交互数据来构造二分图,$\mathcal{G} = \{(u,i)|u \in \mathcal{U},i \in \mathcal{I}\}$,每条边$y_{ui} = 1$对应一条user-item观测数据。除此之外,对于每个item $i$,都有多种模态特征,即:视觉 (visual) 、声觉 (acoustic)、文本 (textual)。具体的,使用$m \in M = \{v,a,t\}$作为模态的indicator,$v, a, t$分别表示视觉、声觉、文本。为了正确捕获特定模态下的用户偏好,作者将$\mathcal{G}$切分为三个子图$\mathcal{G}_m, m \in M$。相比于原图,子图只改变了每个item结点的属性特征,只保留其相对应的模态的特征,而整体的拓扑结构和原图$\mathcal{G}$是一致的。例如$\mathcal{G}_v$下,只有对应的视觉模态特征可以在该子图下使用。
整体的模型结构如下所示,不同模态域的aggregation和combination分别进行,最后相加不同模态域得到的表示作为最终的表示,并通过点乘进行预测。
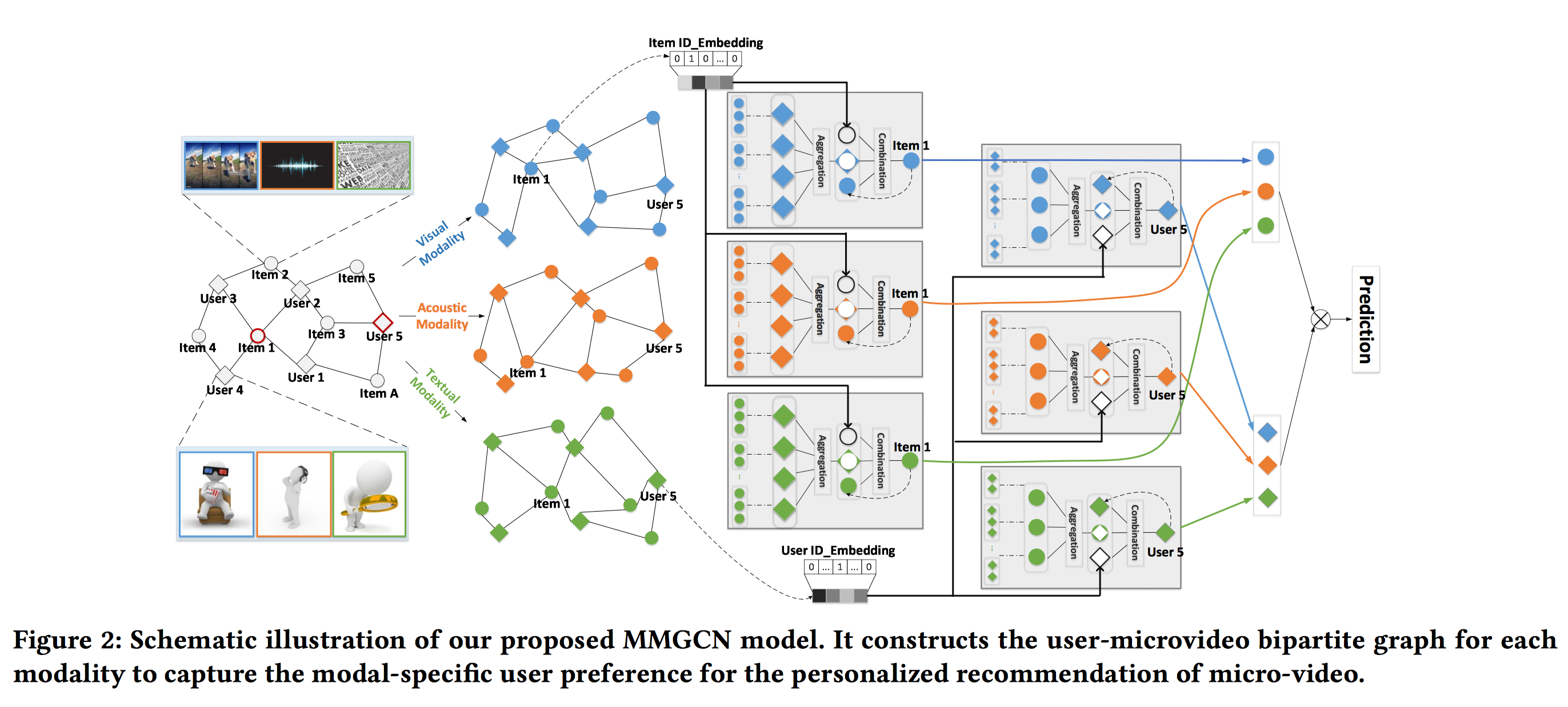
Aggregation Layer
对于用户来说,用户历史interacted item能够反映用户的兴趣,故可以对items进行aggregate操作来丰富user representation;对于物品来说,交互过item的user group可以作为item除自身模态特征之外的补充信息,故可以对users进行aggregate来提升item representation。
基于message-passing机制,对模态子图$\mathcal{G}_m$中,任意一个user或item结点,我们采用一个汇聚函数$f(\cdot)$来量化从邻域结点传播来的信息(representation being propagated)的影响。以user为例,汇聚得到的modal-specific表示如下:
$$
\boldsymbol{h}_m = f(\mathcal{N}_u) \tag{1}
$$
$\mathcal{N}_u = {j|(u, j) \in \mathcal{G}_m }$表示子图$\mathcal{G}_m$ user结点$u$的邻域item结点。$\boldsymbol{h}_m$捕获了结构化特征 (structural information)。
$f(\cdot)$作者采用了两种形式。
Mean Aggregation: 采用average pooling操作来汇聚modal-specific features,再加一个非线性变换。
$$
f_{avg}(\mathcal{N}_u)=\text{LeakyRelu}(\frac{1}{|\mathcal{N_u}|}\sum_{j \in \mathcal{N_u}} \boldsymbol{W}_{1, m} \boldsymbol{j}_m) \tag{2}
$$
$\boldsymbol{j}_m \in \mathbb{R}^{d_m}$ 是模态$m$下item $ j$ 的表示。$\boldsymbol{W}_{1,m} \in \mathbb{R}^{d_m^{\prime} \times d_m}$是线性变换矩阵 (下标1只是编号,代表本文中使用的第一个参数矩阵)。平均池化操作假设了所有邻域结点的影响是等价的。目前的问题是,item $j$在每种模态下都有一种初始表示,究竟是根据item的模态特征得到 (visual下根据帧图像卷积得到特征表示;text下根据文本描述提取特征表示),还是直接指定$|M|$个随机的modal-specific嵌入呢?
答案应该是前者。对于item侧,$\boldsymbol{j}_m$这个实际上就是后文提到的初始化的item intrinsic information $\boldsymbol{i}_m$,是modal pre-extracted feature。(后文实际上没有讲清楚,我是如何知道的?我是看开源的代码实现知道的。一开始我的理解是后者)
Max Aggregation: 使用max pooling操作来进行dimension-aware特征选择,
$$
f_{max}(\mathcal{N}_u) = \text{LeakyReLU}(max_{j \in \mathcal{N}_u} \boldsymbol{W}_{1,m} \boldsymbol{j}_m) \tag{3}
$$
这样的好处是不同的邻域结点的影响力不同。
item结点的aggregate操作同理。同样的,目前的问题是每个用户在每种模态下的初始表示是什么?是直接指定$|M|$个随机的modal-specific嵌入吗?答案是的,modal-specific嵌入,但是这里也是指后文提到的user intrinsic information $\boldsymbol{u}_m$,只不过作者用的随机初始化的向量来表示(可能是因为缺乏user profile信息)。
Combination Layer
这个层的目标是融合aggtegation layer得到的来自邻域结点的结构化信息 (structural information) $\boldsymbol{h}_m$,结点自身内在信息 (intrinsic information) $\boldsymbol{u}_m$ 以及沟通不同模态的联系信息 (modality connection information) $\boldsymbol{u}_{id}$。形式化为:
$$
\boldsymbol{u}_m^{(1)} = g(\boldsymbol{h}_m, \boldsymbol{u}_m, \boldsymbol{u}_{id}) \tag{4}
$$
$\boldsymbol{u}_m \in \mathbb{R}^{d_m}$和上述提到的$\boldsymbol{j}_m$同理,是user的初始modal-specific表示,只不过作者实际上采用的是随机初始化方式,而$\boldsymbol{j}_m$是pre-extracted item modal-features。$\boldsymbol{u}_{id} \in \mathbb{R}^d$是$d$维user ID的嵌入表示,是所有模态间共享的,作为沟通不同模态信息的桥梁。
对于$g$函数的设计,
作者首先将$\boldsymbol{u}_m$和$\boldsymbol{u}_{id}$融合起来,即将$\boldsymbol{u}_m$通过非线性变换映射到$d$维空间,再加上$\boldsymbol{u}_{id}$。
$$
\hat{\boldsymbol{u}}_m=\text{LeakyRelu}(\boldsymbol{W}_{2,m} \boldsymbol{u}_m) + \boldsymbol{u}_{id} \tag{5}
$$
$\boldsymbol{W}_{2,m} \in \mathbb{R}^{d \times d_m}$。这样子变换完后,不同的模态信息在同一个超平面上了,是可比的。$\boldsymbol{u}_{id}$的好处是沟通了不同模态表示之间的差距,同时在反向传播的过程中,信息可以跨模态进行传播(the ID embedding $\boldsymbol{u}_{id}$ essentially bridges the gap between modal-specific representations, and propagates information across modalities during the gradient back-propagation process.)。形象的说,例如,视觉模态$v$下的反向传播误差能影响$\boldsymbol{u}_{id}$,$\boldsymbol{u}_{id}$又能进一步影响模态$t$下的modal-specific参数。这样就达到了不同模态之间互相联系。接着将$\hat{\boldsymbol{u}}_m$和$\boldsymbol{h}_m$融合起来,进一步分为了两种:
Concatenation Combination:
$$
g_{co} (\boldsymbol{h}_m , \boldsymbol{u}_m , \boldsymbol{u}_{id}) = \text{LeakyReLU} \left(\boldsymbol{W}_{3,m} (\boldsymbol{h}_m || \hat{\boldsymbol{u}}_m)\right) \tag{6}
$$
$||$是concat操作,$\boldsymbol{W}_{3,m} \in \mathbb{R}^{d_m^{\prime} \times (d_{m}^{\prime} +d)}$。Element-wise Combination:
$$
g_{ele}(\boldsymbol{h}_m , \boldsymbol{u}_m , \boldsymbol{u}_{id}) = \text{LeakyReLU}(\boldsymbol{W}_{3,m} \boldsymbol{h}_m + \hat{\boldsymbol{u}}_m) \tag{7}
$$
$\boldsymbol{W}_{3,m} \in \mathbb{R}^{d \times d^{\prime}_m}$。加法即element-wise feature interaction between two representation。而concat中两种表示之间独立。
第$l$层的combination layer的输出,即$g$的输出,对于user,作者用$\boldsymbol{u}_m^{(l)}$表示;对于item,作者用$\boldsymbol{i}_m^{(l)}$表示。
Recursion Formula
叠加多层aggregation layer和combination layer,递推式子如下:
$$
\boldsymbol{h}_m^{(l)}=f(\mathcal{N}_u), \boldsymbol{u}_m^{(l)} = g(\boldsymbol{h}_m^{(l)} , \boldsymbol{u}_m^{(l-1)} , \boldsymbol{u}_{id}) \tag{8}
$$
此处有个关键性的描述段落,指明了每个变量的含义,尤其是$\boldsymbol{u}_m$,原文讲的比较清楚,由于很重要,先摘录下来。
where $\boldsymbol{u}_m$ is the representation generated from the previous layer, memorizing the information from her $(l − 1)$-hop neighbors. $\boldsymbol{u}_m^{(0)}$ is set as $\boldsymbol{u}_m$ at the initial iteration. Wherein, user $u$ is associated with trainable vectors $\boldsymbol{u}_m$ , $\forall m \in M$, which are randomly initialized; whereas, item $i$ is associated with pre-extracted features $\boldsymbol{i}_m$ , $\forall m \in M$. As a result, $\boldsymbol{u}_m^{(l-1)}$ characterizes the user preferences on item features in modality $m$, and considers the influence of modality interactions that reflect the underlying relationships between modalities.
注意上述加粗的部分,对于user来说,初始化的intrinsic information $\boldsymbol{u}_m^{(0)}$使用随机初始化的modal-specific $\boldsymbol{u}_m$;对于item来说,初始化的intrinsic information $\boldsymbol{i}_m^{(0)}$使用预先提取的模态特征$\boldsymbol{j_m}$(原文写的是$\boldsymbol{i_m}$,我结合了开源代码,个人认为是笔误)。
$\boldsymbol{u}_m^{(l)}$构成:
- 融合了从item侧汇聚到的modal m-specific模态信息$\boldsymbol{h}^{(l)}$。
- 自身的modal-specific信息$\boldsymbol{u}_m^{(l-1)}$(第$l-1$的combination layer的输出,类似self-connection操作)
- 跨模态的联系信息$\boldsymbol{u}_{id}$。
因此作者说$\boldsymbol{u}_m^{(l-1)}$不仅刻画了用户对于模态$m$下item特征的偏好,还考虑了跨模态之间的交互信息的影响力。
以user为例,可以看出,随着GNN层数的增加,$\boldsymbol{h}_m^{(l)} , \boldsymbol{u}_m^{(l-1)}$是迭代的形式,$\boldsymbol{u}_{id}$是共享不变的。$\boldsymbol{u}_m^{(l)}$的迭代形式公式8交代的很清楚。而$\boldsymbol{m}^{(l)}$的迭代形式,作者没有说明清楚,实际上$\boldsymbol{h}_m^{(l)}$是关于$\boldsymbol{i}_m^{(l-1)}$的函数,即item侧第$l-1$的combination layer的输出,更准确的递推式,$\boldsymbol{h}_m^{(l)}=f(\mathcal{N}_u, \boldsymbol{i}_m^{(l-1)})$。
进一步可以观察下作者在github的代码实现,核心forward,
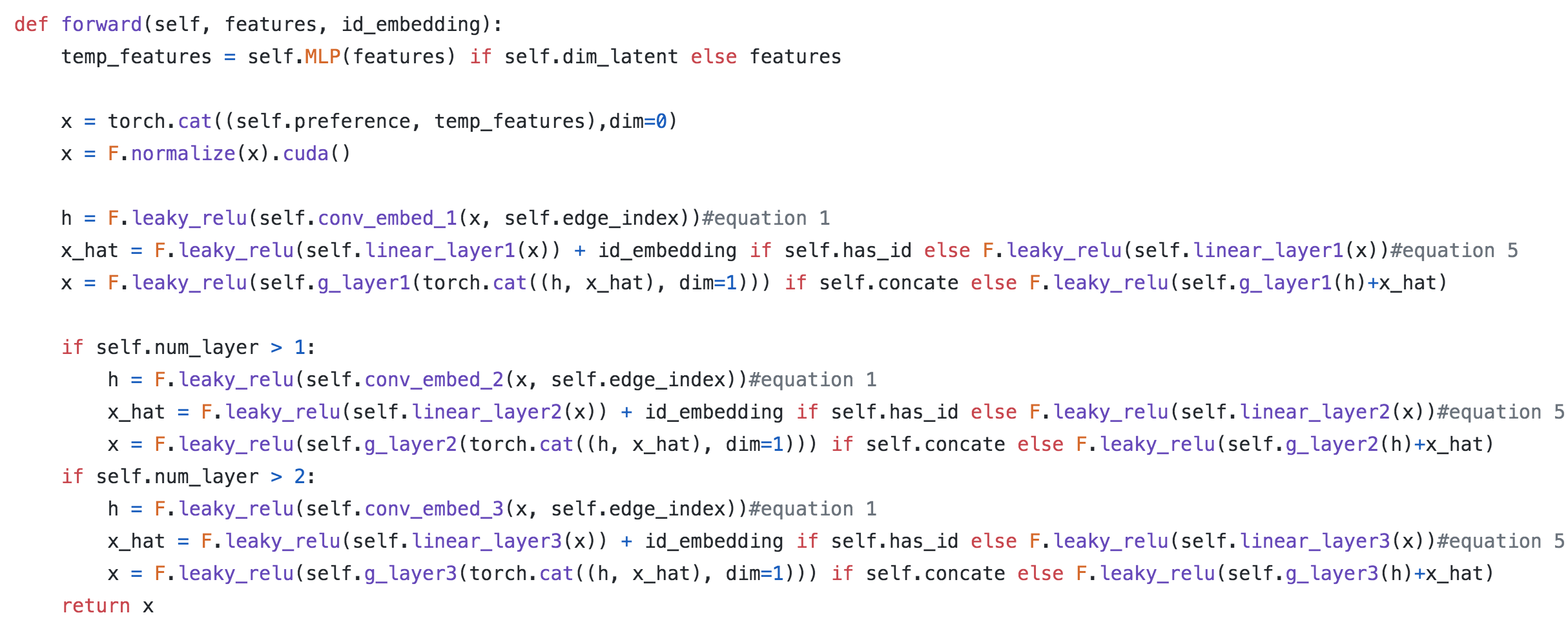
可以重点关注下$x$,初始是features;第一层输出的$x$作为第二层的输入,以此类推。
Model Prediction
上述总共叠加了$L$层。最后,作者累加了所有模态下最后一个GNN层的输出,作为user或item最终的表示,
$$
\boldsymbol{u}^{\star} = \sum_{m \in M}\boldsymbol{u}_m^{(L)}, \boldsymbol{i}^{\star} = \sum_{m \in M}\boldsymbol{i}_m^{(L)} \tag{9}
$$
预测user-item pair的话,使用二者点乘形式进行预测,${\boldsymbol{u}^{\star}}^T \boldsymbol{i}^{\star}$。
最后作者使用和NGCF一样的BPR Loss进行优化。不再累赘。
Experiment
在实验部分作者使用了头条数据集tiktok,快手数据集Kwai,movie-lens进行实验。头条数据集3种模态都有,快手只有文本和图像。movie-lens作者手动爬取了youtube的预告片,并用resnet50提取关键帧的特征,使用FFmpeg抓取声音片断并用VGGish提起声音特征,使用Sentence2Vector从文本描述中提取特征。这个工作量是真大。
另外,作者评估的时候,对于测试集中每个正样本observed user-item pair,随机抽了1000个unobserved user-item pairs作为负样本,然后用precision@k, recall@k, ndcg@k进行评估。这个是可取的,但是很多方法都是在全域进行评估,即,所有的unobserved user-item pairs全部作为负样本,这样的评估显然更客观,也更有说服力。
作者可视化用户对同1个item的不同模态的特征的偏好不一致性也值得学习。通过分析学习到的item的多模态降维表示,并抽取部分用户交互过的item,看交互过的item的降维表示的分布情况,例如,在视觉模态下,交互过的item比较分散,说明这些items的封面/帧/图像差异较大;而文本模态下,交互过的item表示向量点比较集中。则说明了用户对视觉模态没有太多的偏好,不是对其兴趣起决定性作用;而对文本域的模态有典型的偏好,例如喜欢看浪漫主题的电影。如下图中的user 1,左图视觉域点分布很分散;右图文本域集中在war和romance主题。相反,有的人可能很关注视觉模态,比如爱看封面美女的电影,那么其视觉模态下的表示就很集中;而可能这些电影主题差异很大,即文本模态下很分散。
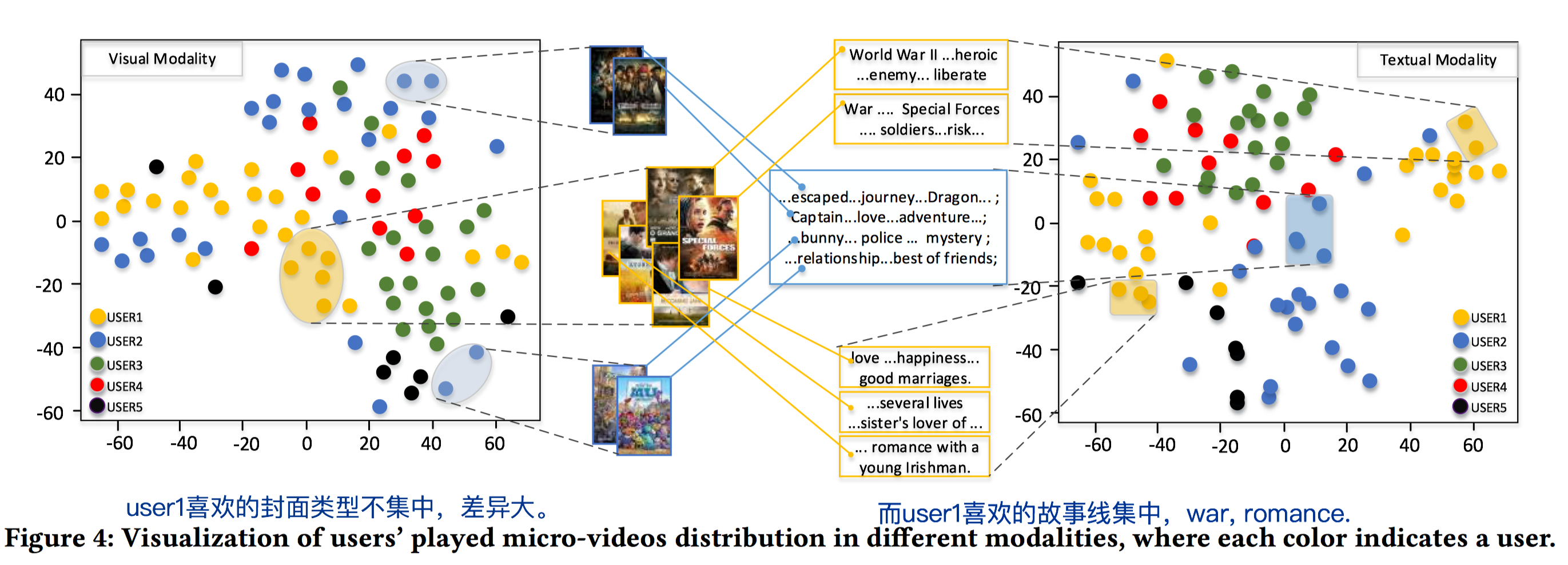
Discussion
作者没有讨论参数复杂度。这里面有非常多的参数。尤其是针对每个user和item的modal-specific参数,即带$m$下标的参数,尤其是user侧,如$\boldsymbol{u}_m^{0}$,全局的$\boldsymbol{u}_{id}$ 。我个人对此保持疑惑,因为在大规模的推荐系统中,user的数量非常多,而交互数据又非常稀疏。给每个user都分配如此多的参数,很多参数估计都得不到很好的学习,同时训练速度也很慢。可能user侧也需要引入profile信息比较好。另外,不是所有的items都有丰富的模态特征,大部分items可能缺乏模态特征,即,不同子图的拓扑结构可能会因为结点缺失相应的特征而导致不相同,这种情况下如何处理呢?
Extensions
除了上述三个工作,关于二分图表示学习的最新工作还包括:
- LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation,将non-linear和feature transformation去掉,只增加一组权重系数来weighted aggregate不同gcn层输出的嵌入为最终的嵌入,大大简化了模型,反而在推荐性能上有提升。这个工作虽然简单,但挺有意思的,有很多intuition和Interpretability的观点,对于理解GCN如何更好的应用于推荐系统挺有帮助的。
- AAAI2020, Revisiting Graph based Collaborative Filtering: A Linear Residual Graph Convolutional Network Approach,同样讨论了去掉non-linear的好处,使用多层的gcn时,通过代入迭代式,可以将不同层的多个feature transformation matrices约减为1个feature transformation matirx,大大减少了参数量。同时讨论了残差方法,传统的方法一般只使用最后一层GCN层输出的user 和 item embedding进行点乘预测评分。而使用残差方法,预测评分的时候,所有的gcn层都一起预测评分,下一个gcn层去预测前一个层剩余的评分残差。这种方式等价于将所有层输出的embedding concat在一起作为final embedding后,再进行点乘预测,也就是NGCF中的预测方法满足了残差预测。直觉来源在于,一方面,叠加gcn layer等价于使用拉普拉斯平滑 (graph operator),故传统方法叠加太多的层的时候,会导致over smoothness问题,故不宜叠加太多,一般1~2层最优。另一方面,0层的时候等价于BPR方法(使用BPR Loss时),也能够得到非常好的预测结果,所以层数低已经具备非常强的能力了。因此可以让后面的gcn层只去预测前面层的残差,这样可以使得层数更深时效果不减。通过观察发现使用残差预测时,深层输出的embedding不会过于平滑,因此预测效果更好。
这两个工作主要借鉴了ICML2019: Simplifying Graph Convolutional Networks,讨论了如何简化GCN,使得更好的应用在推荐系统中二分图的表示学习。
Summary
关于图二分图的挖掘,是推荐系统中的核心问题之一。传统的图表示学习直接对二部图进行挖掘是有问题的。个人认为传统的graph embedding在建模时实际上很依赖于graph的手动构造,连边权重的合理设置,且没有把二分图中的collaborative signals直接建模到结点的embedding表示中,而只是通过目标函数来间接引导。而二分图的构建是基于原始数据的,没有连边权重,且数据过于稀疏,蕴含在二分图中的协同信息是非常隐晦的和难以挖掘的,故传统的图表示学习方法很难处理。本篇文章中介绍的三个工作基于message passing范式的GNN来挖掘二分图,将collaborative signals直接建模到embedding中,这是非常值得借鉴的。另外,这几篇文章的github都有源码,值得学习和实践。
References
KDD2018,GCMC:Graph Convolutional Matrix Completion
SIGIR2019,NGCF:Neural Graph Collaborative Filtering
MM2019,MMGCN: Multi-modal Graph Convolution Network for
Personalized Recommendation of Micro-video
Github, GCMC, Source Code
Github, NGCF, Source Code
从 Graph Convolution Networks (GCN) 谈起
LightGCN: Simplifying and Powering Graph Convolution Network for Recommendation

