前文提到的PCA是一个信息提取的过程,将原始数据进行降维。而本文提到的独立成分分析ICA(Independent Components Analysis)是一个信息解混过程,ICA认为观测信号是若干个统计独立的分量的线性组合。即假设观察到的随机信号x服从模型\(x=As\),其中s为未知源信号,其分量(代表不同信号源)相互独立,A为一未知混合矩阵(As实现不同信号源的线性组合)。ICA的目的是通过且仅通过观察x来估计混合矩阵A以及源信号s。
引入
让我们从经典的鸡尾酒宴会问题(cocktail party problem)谈起。假设在宴会中有n个人,他们可以同时说话,我们也在房间中的一些角落共放置了n个声音接收器(microphone)用来记录声音。宴会过后,我们从n个麦克风中得到了一组数据\(\{x^{(i)}\left(x_1^{(i)},x_2^{(i)},…,x_n^{(i)}\right),i=1,2,…m\}\),上标i代表采样的时间顺序,每个时刻n个声音组合得到1组样本,并且在每个时刻,每个麦克风都会得到一种n个声音的线性组合,也就是说每组样本包含了n种线性组合,m个时刻共得到了m组采样,并且每一组采样都是n维的。我们的目标是单单从这m组采样数据中分辨出每个人说话的信号。
将问题细化一下,有n个信号源\(s(s_1,s_2,…,s_n)^T,s \in \mathbb{R}^n\),每一维都是一个人的声音信号,每个人发出的声音信号独立。s是一个矩阵,假设m组样本,则s规格为\(n*m\),每一行代表一个人m个时刻的声音序列,总共有n行,即n个人的声音序列。A是一个未知的混合矩阵(mixing matrix),用来组合叠加信号s,矩阵计算相当于s进行了线性组合,线性组合的系数由混合矩阵A来决定的。则:
$$x=As$$
x的意义在上文解释过,这里的x不是一个向量,是一个矩阵,其中每个列向量是\(x^{(i)},x^{(i)}=As^{(i)}\),\(x^{(i)}\)列向量是n维的,即n个接收器在i时刻接收到的序列,\(x^{(i)}\)每个分量代表i时刻不同接收器得到的所有n个声音的线性组合。例如第一个分量代表第一个接收器在第i时刻接收到的所有声音的线性组合,第n个分量代表第n个接收器在i时刻接收到的所有声音的线性组合。
表示成图如下: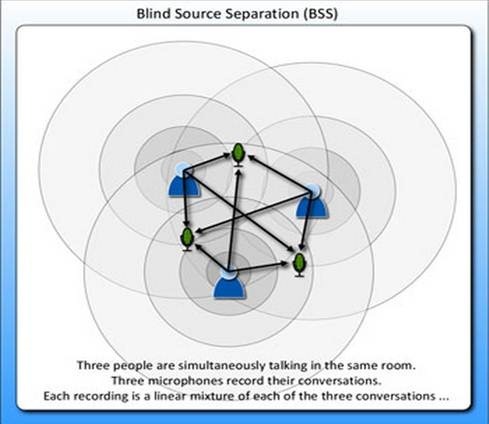
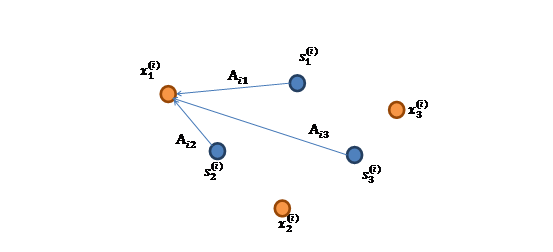
\(x^{(i)}\)的每个分量都由\(s^{(i)}\)的分量线性表示。A和s都是未知的,x是已知的,我们要想办法根据x来推出s。这个过程也称作盲信号分离。
令\(W=A^{-1}\),那么\(s^{(i)}=A^{-1}x^{(i)}=Wx^{(i)}\),则可将W表示成:
$$W=\begin{bmatrix}——w_1^T—— \\\ … \\\ ——w_n^T—— \end{bmatrix}$$
其中,\(w_i \in \mathbb{R}^n\),显然W是\(n*n\)规格的。得到:
$$s_j^{(i)}=w_j^{T}x^{(i)}$$
ICA的不确定性
由于w和s都不确定,那么在没有先验知识的情况下,无法同时确定这两个相关参数。比如上面的公式s=wx。当w扩大两倍时,s只需要同时扩大两倍即可,等式仍然满足,因此无法得到唯一的s。同时如果将人的编号打乱,变成另外一个顺序,如上图的蓝色节点的编号变为3,2,1,那么只需要调换A的列向量顺序即可,因此也无法单独确定s。这两种情况称为原信号不确定。
还有一种ICA不适用的情况,那就是信号不能是高斯分布的。假设只有两个人发出的声音信号符合多元正态分布\(s \sim N(0,I)\),I是\(2*2\)的单位矩阵,s的概率密度函数以均值0为中心,投影面是椭圆的山峰状,因为\(x=As\),因此x也是高斯分布的,均值为0,协方差为\(E[xx^T]=E[Ass^TA^T]=AA^T\)。
令R是正交阵(\(RR^T=R^TR=I\)),令\(A’=AR\),如果将\(A\)替换成\(A’\)。那么\(x’=A’s\),s的分布仍然是多元高斯分布,则\(x’\)的均值仍然为0,协方差为:
$$E[x’(x’)^T]=E[A’ss^T(A’)^T]=E[ARss^T(AR)^T]=ARR^TA^T=AA^T$$
因此,不管混合矩阵是\(A\)还是\(A’\),x的分布情况是一样的,此时混合矩阵不是唯一的,因此无法确定原信号。
密度函数与线性变换
在讨论ICA算法之前,我们先来回顾一下概率和线性代数里的知识。
假设我们的随机变量s有概率密度函数\(p_s(s)\)(连续值是概率密度函数,离散值是概率)。为了简单,我们再假设s是实数,有一个随机变量\(x=As\),A和x都是实数。令\(p_x\)是x的概率密度,那么怎么求\(p_x\)呢?
令\(W=A^{-1}\),首先将式子变幻成\(s=Wx\),然后得到\(P_x(x)=p_s(Ws)\),求解完毕。可惜这种方法是错误的。比如s符合均匀分布的话,即\(s \sim Uniform[0,1]\),那么s的概率密度\(P_s(s)=1\{0 \leq s \leq 1\}\),现在令A=2,即\(x=2s\),也就是说x在[0,2]上均匀分布,则\(p_x(x)=0.5\),因此,按照前面的推导会得到\(p_x(x)=p_s(0.5s)=1\),显然是不对的。正确的公式是:\(p_x=p_s(Wx)|w|\)
推导方法如下:
$$F_X(a)=P(X \leq a)=P(AS \leq a)= p(s \leq Wa)=F_s(Wa) \\\\
p_x(a)=F_X’(a)=F_S’(Wa)=p_s(Wa)|W|$$
更一般地,如果s是向量,A是可逆的方阵,那么上式仍成立。
ICA算法
ICA算法归功于Bell和Sejnowski,这里使用最大似然估计来解释算法,原始的论文中使用的是一个复杂的方法Infomax principal。
我们假定每个\(s_i\)有概率密度\(p_s\),那么给定时刻原信号的联合分布是:
$$p(s)=\prod_{i=1}^n p_s(s_i)$$
这个公式有一个假设前提:每个人发出的声音信号各自独立。有了p(s),我们可以求得p(x):
$$p(x) = p_s(Wx)|W|=|W|\prod_{i=1}^n p_s(w_i^T x)$$
左边是每个采样信号x(n维向量)的概率,右边是每个原信号概率乘积的|W|倍。
前面提到过,如果没有先验知识,我们无法求得W和s。因此我们需要知道\(p_s(s_i)\),我们打算选取一个概率密度函数赋给s,但是我们不能选取高斯分布的密度函数。在概率论里面,我们知道密度函数p(x)由累积分布函数(CDF)F(x)求导得到。F(x)要满足两个性质是,单调递增和取值范围在[0,1]。我们发现sigmoid函数很适合,定义域为负无穷到正无穷,值域为0到1,缓慢递增。我们假定s的累积分布函数符合sigmoid函数:
$$g(s)=\frac{1}{1+e^{-s}}$$
求导后:
$$P_s(s)=g’(s)=\frac{e^s}{(1+e^s)^2}$$
这就是s的密度函数,这里s是实数。
如果我们预先知道s的分布函数,那就不用假设了。但是在缺失的情况下,sigmoid函数能够在大多数问题上取得不错的效果。由于上式中P_s(s)是个对称函数,因此E[s]=0,那么\(E[x]=E[As]=0\),x的均值也为0.
知道了\(p_s(s)\),就剩下W了。给定采样后的训练样本\(\{x^{(i)}(x_1^{(i)},x_2^{(i)},…,x_n^{(i)},i=1,2…,m\}\),样本对数似然估计如下,使用前面得到的x的概率密度函数:
$$\ell(W)=\sum_{i=1}^m \left(\sum_{j=1}^n log \ g’(w_j^T x^{(i)}) + log |W| \right)$$
接下来就是对W球到了,这里牵涉一个问题就是对行列式|W|进行求导的方法,属于矩阵微积分。这里先给出结果:
$$\nabla_w|W|=|W|(W^{(-1)})^T$$
最终得到的求导公式如下,\(log g’(s)\)的导数是\(1-2g(s)\)(可以自己验证):
$$W:=W+\alpha \left(\begin{bmatrix}1-2g(w_1^T x^{(i)}) \\\ 1-2g(w_2^T x^{(i)}) \\\ … \\\ 1-2g(w_n^T x^{(i)})\end{bmatrix} {x^{(i)}}^T+(W^T)^{-1} \right)$$
其中\(\alpha\)是梯度上升速率,人为指定。
当迭代求出W后,便可得到\(s^{(i)}=Wx^{(i)}\)来还原出原始信号。
注意:我们计算最大似然估计时,假设了\(x^{(i)}和x^{(j)}\)之间是独立的,然而对于语音信号或者其他具有时间连续依赖特性(如温度),这个假设不成立。但是在数据足够多时,假设独立对效果影响不大,同时如果事先打乱样例,并运行随机梯度上升算法,那么就能够加快收敛速度。
回顾鸡尾酒宴会问题,s是人发出的信号,是连续值,不同时间点的s不同,每个人发出的信号之间独立(\(s_i和s_j\)之间独立)。s的累积概率分布韩式sigmoid函数,但是所有人发出声音信号都符合这个分布。A(W的逆矩阵)代表了s相对于x的位置变化,x是s和A变化后的结果。
实例
当n=3时,原始信号正弦、余弦、随机信号。如下图所示,也就相当于S矩阵: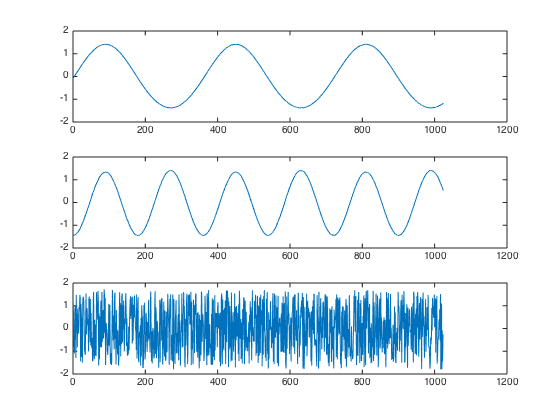
经过随机混合,由6个麦克风录制下来,观察到的x信号如下,相当于X矩阵: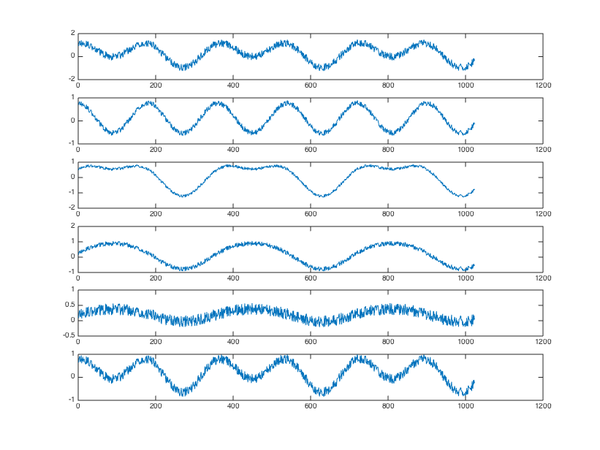
在使用ICA算法之前,需要对数据进行预处理,可使用PCA和白化。PCA、白化处理后,可以看到6路信号减少为3路,ICA仅需要这3路混合信号即可还原源信号。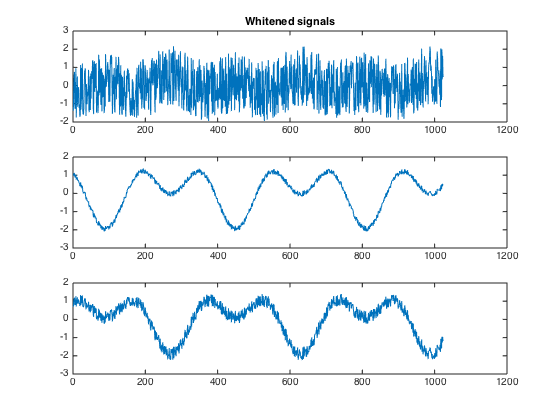
使用ICA算法,进行多步迭代优化,就会按照信号之间独立最大的假设,将信号解混输出。得到原始S信号如下图所示: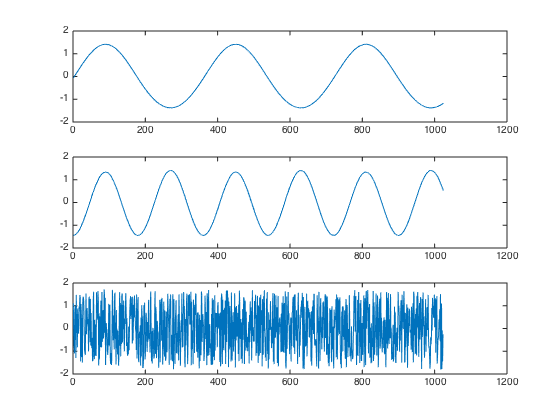
PCA和ICA的联系和区别
不管是PCA还是ICA,都不需要你对源信号的分布做具体的假设;如果观察到的信号为高斯,那么源信号也为高斯,此时PCA和ICA等价。下面稍作展开。
假设你观察到的信号是n维随机变量\(x=(x_1,\ldots,x_n)^T\).主成分分析(PCA)和独立成分分析(ICA)的目的都是找到一个方向,即一个n维向量\(w=(w_1,\ldots,w_n)^T\)使得线性组合\(\sum_{i=1}^nw_ix_i=w^Tx\)的某种特征最大化。
PCA
PCA认为一个随机信号最有用的信息体包含在方差里。为此我们需要找到一个方向\(\mathbf{w}_1\),使得随机信号x在该方向上的投影\(w_1^Tx\)的方差最大化。接下来,我们在与\(w_1\)正交的空间里到方向\(w_2\),使得\(w_2^Tx\)的方差最大,以此类推直到找到所有的n个方向\(w_1,\ldots,w_n\). 用这种方法我们最终可以得到一列不相关的随机变量:\(w_1^Tx,\ldots,w_n^Tx\)。
如果用矩阵的形式,记\(W=(w_1,\ldots, w_n)\),那么本质上PCA是把原随机信号x变换成了\(y=Wx\),其中y满足,y的各分量不相关以及\(y_1,\ldots,y_n\)的方差递减。
特别地,当原随机信号x为高斯随机向量的时候,得到的y仍为高斯随机向量,此时它的各个分量不仅仅是线性无关的,它们还是独立的。
通过PCA,我们可以得到一列不相关的随机变量。至于这些随机变量是不是真的有意义,那必须根据具体情况具体分析。最常见的例子是,如果x的各分量的单位(量纲)不同,那么一般不能直接套用PCA。比如,若x的几个分量分别代表某国GDP, 人口,失业率,政府清廉指数,这些分量的单位全都不同,而且可以自行随意选取:GDP的单位可以是美元或者日元;人口单位可以是人或者千人或者百万人;失业率可以是百分比或者千分比,等等。对同一个对象(如GDP)选用不同的单位将会改变其数值,从而改变PCA的结果;而依赖“单位选择”的结果显然是没有意义的。
ICA
ICA又称盲源分离(Blind source separation, BSS),它假设观察到的随机信号x服从模型,其中s为未知源信号,其分量相互独立,A为一未知混合矩阵。ICA的目的是通过且仅通过观察x来估计混合矩阵A以及源信号s。大多数ICA的算法需要进行“数据预处理”(data preprocessing):先用PCA得到y,再把y的各个分量标准化(即让各分量除以自身的标准差)得到z。预处理后得到的z满足下面性质:z的各个分量不相关;z的各个分量的方差都为1。
有许多不同的ICA算法可以通过z把A和s估计出来。以著名的FastICA算法为例,该算法寻找方向使得随机变量\(w^Tz\)的某种“非高斯性”(non-Gaussianity)的度量最大化。一种常用的非高斯性的度量是四阶矩\(\mathbb{E}[(w^Tx)^4]\)。类似PCA的流程,我们首先找\(w_1\)使得\(\mathbb{E}[(w_1^Tx)^4]\)最大;然后在与\(w_1\)正交的空间里找\(w_2\),使得\(\mathbb{E}[(w_2^Tx)^4]\)最大,以此类推直到找到所有的\(w_1,w_2…,w_n\). 可以证明,用这种方法得到的\(w_1^T z,…,w_n^T z\)是相互独立的。
ICA认为一个信号可以被分解成若干个统计独立的分量的线性组合,而后者携带更多的信息。我们可以证明,只要源信号非高斯,那么这种分解是唯一的。若源信号为高斯的话,那么显然可能有无穷多这样的分解。

