图表示学习Encoder-Decoder框架介绍和拓展

本篇文章主要从一篇关于Graphs的表示学习的调研文章出发，介绍基于Graph表示学习的一个Encoder-Decoder框架，该框架可以启发关于Graph表示学习的研究切入点以及良好的编程实践。此外，本文还围绕目前主流的一些Graph Embedding或Graph Neural Networks方法，来探讨如何使用Encoder-Decoder框架来重新组织和提炼方法中的核心思想和核心步骤，这对于改进模型和编程实践有非常好的借鉴意义。

Survey

2017: Representation learning on graphs: Methods and applications

下面主要围绕graph表示学习的问题定义，主流方法分类，encoder-decoder框架展开来介绍这篇调研paper.

Problem Definition

Graph机器学习的核心问题：如何把Graph结构信息纳入机器学习模型中。常用的Graph结构信息包括：节点的全局位置 (Global Position) 和节点的局部近邻结构 (The structure of the node’s local graph neighborhood) 等。
Graph Embedding的目标：学习node或entire(sub)graph的低维embedding，使得embedding space中的几何关系能够反映原始Graph的结构信息，如两个node节点在embedding space中的距离能够反映原始高维空间Graph中二者的相似性。（Learn embeddings that encode graph structure）

Method Categories

目前主流的Graph Embedding方向是Node Embedding，包含了3大类主流方法：Matrix Factorization、Random Walk、Graph Convolution Networks。

Matrix Factorization：矩阵分解。将Graph结构信息使用矩阵来刻画，例如Graph邻接矩阵或节点的共现矩阵，衡量了所有节点之间的相似性，对该矩阵进行分解，学习节点的低维向量表示。例如：Graph Laplacian Eigenmaps、Graph Factorization。
Random Walk：随机游走。构建Graph中Node的随机游走序列，构建游走序列内部节点之间的上下文共现对，再使用Word2Vec方法进行学习。例如：DeepWalk、Node2Vec。
Graph Convolutional Networks：Graph卷积网络。将卷积从Image/Sentence拓展到Graph。基于节点local Neighborhoods的汇聚。例如：GCN、GraphSAGE。

Encoder-Decoder Framework

作者针对Node Embedding，提出了一个统一的Encoder-Decoder编程框架来设计和实现Graph Embedding算法，上述所述目前主流的Graph Embedding算法都可以使用该框架来重新组织代码结构。

Encoder：目标是将每个Node映射编码成低维的向量表示，或embedding。
Decoder：目标是利用Encoder输出的Embedding，来解码关于图的结构信息。

这一框架的核心思想在于，如果我们能够基于编码得到的低维embeddings，来学习高维Graph结构信息的解码，这些信息包括节点的全局位置或节点的局部近邻结构等，那么，原则上，这些低维emebdding包含了所有下游机器学习任务所需要的全部信息。

形式化地，Encoder是如下映射函数：
$$
ENC: \mathcal{V} \rightarrow \mathbb{R}^d
$$
即，将节点 $i \in \mathcal{V}$ 映射成embedding $\boldsymbol{z}_i \in \mathbb{R}^d$。

Decoder是这样一个函数，函数的输入是上述node emebddings集合，输出是要解码的、用户自定义的Graph结构信息。例如：Decoder目标可能是预测在给定节点embedding条件下，节点之间的连边是否存在；或给定embeddings下，预测节点所属的社区类别。Decoder的形式是多样化的，但是最常用的是pairwise decoder，
$$
DEC: \mathbb{R}^d \times \mathbb{R}^d \rightarrow \mathbb{R}^+
$$
即，Decoder的输入是Node Pair的embeddings，输出是一个实数，衡量了这两个Node在原始Graph中的相似性。

为了学习emebdding，我们的目标是重构节点低维emebddings的相似性，以反映二者在原始Graph中的相似性。即给定Node Pair $(v_i,v_j)$,
$$
DEC(ENC(v_i), ENC(v_j)) = DEC(\boldsymbol{z}_i,\boldsymbol{z}_j) \approx s_{\mathcal{G}}(v_i, v_j)
$$
其中，$DEC(\boldsymbol{z}_i,\boldsymbol{z}_j)$是模型基于编码的embedding，解码得到的二者的相似性（Estimated）；而$s_{\mathcal{G}}$是用于定义的、原始图中，顶点之间的相似性（Ground Truth），例如可以使用邻接矩阵$A$来表示。那么，学习的目标就是所有训练集Node Pairs上，上述重构误差最小化，
$$
\mathcal{L} = \sum_{(v_i,v_j) \in \mathcal{D}} \ell (DEC(\boldsymbol{z_i}, \boldsymbol{z_j}), s_{\mathcal{G}}(v_i,v_j))
$$
$\ell: \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}$是用于定义的损失函数，衡量了两个输入之间的差异。例如可以使用平方损失或交叉熵损失等。其中，$DEC(z_i, z_j)$可以看做是估计的(相似)值；$s_{\mathcal{G}}(v_i,v_j)$可以看做是真实的(相似)值。

上述框架涉及到4大组件：

Pairwise Similarity Function $s_{\mathcal{G}}: \mathcal{V} \times \mathcal{V} \rightarrow \mathbb{R}^+$，定义在原始Graph上，衡量了节点之间的相似性。可以看做是pairwise “ground truth” label在Loss中使用，只不过这个ground truth通常是无监督的，反映了原始图的拓扑结构。
Encoder Function，$ENC$，产生节点的embedding。这个函数包含了训练参数，最常使用的是embedding lookup操作，即每个节点学习一个自己的embedding表示，不同节点之间不存在参数共享。在decoder中使用。
Decoder Function，$DEC$，基于embeddings，重构Node相似性。通常不包含训练参数。例如使用点乘、欧式距离等来表示相似性。可以看做是estimated label在Loss中使用，定义了node pair在embedding空间的相似性。
Loss Function，$\ell$，评判重构好坏，即对比$DEC(\boldsymbol{z_i}, \boldsymbol{z_j})$和$s_{\mathcal{G}}(v_i,v_j)$。融合了decoder的estimated label和pairwise similarity function的ground truth label来构造损失，指导学习。

目前基于矩阵分解，随机游走的方法都可以使用上述框架来抽象，并且其encoder都是浅层的embedding，即，使用embedding lookup，每个节点学习一个自己的emebdding，不同节点不进行参数共享，如下表：

例如：Laplacian Eigenmaps（谱聚类用的方法）的Decoder使用的是欧式距离，相似性度量可以使用任何方法（例如邻接矩阵，每个元素为$w_{ij}$），损失函数形如$\ell=w_{ij}(z_i-z_j)^2$，即两个节点相似性越大，施加大的权重，使得模型学习到的二者embedding更近。再比如DeepWalk使用$\text{softmax}(z_i^T z_j)$作为Decoder，而相似性度量是基于条件概率分布$P_{\mathcal{G}}(v_j|v_i)$，这个分布是指以$v_i$为起点，访问到$v_j$的概率，通过采样节点序列并构造共现对来近似的，而损失函数使用的是交叉熵损失。具体实现时，通常使用$\mathcal{L}=\sum_{(v_i, v_j) \in \mathcal{D}} -\log(\text{DEC}(\boldsymbol{z}_i, \boldsymbol{z}_j))$，其中， $(v_i,v_j) \sim P_{\mathcal{G}}(v_j|v_i)$，是通过随机游走在Graph采样得到的。

此外，GNN的方法实际上也能用上述框架来抽象，将在拓展一节介绍。

上述浅层的embedding的缺点：

节点的encoder没有参数共享，当Graph很大、节点很多时，每个节点学习一个embedding，会导致参数过多，即$O(|\mathcal{V}|)$的参数量。
不能建模Node的Attribute。但是有时候Node的Attribute很重要。目前使用到的方法可以认为只使用了节点的ID或节点的one-hot表示，而其他属性都没有使用。
不能拓展到Graph动态变化的场景（Transductive），例如新节点。说白了就是类似冷启动的场景。

为了解决上述问题，目前有几种方案：

Structural Deep Network Embeddings (SDNE) 把graph的structure在节点encoder的时候使用到。使用的是AutoEncoder，节点的原始输入经过encoder后再decoder，decoder的结果与原始输入越接近越好，原始输入通常使用某个节点和其邻居节点的相似度值集合来表示。此时SDNE的解码器是unary decoder，即不是上文提到的pairwise decoder。$DEC ( ENC (s _i )) = DEC (z_i ) ≈ s_i$。$s_i$即节点$i$和邻居节点的相似值。Loss为：$\mathcal{L}=\sum_{v_i \in \mathcal{V}} ||DEC(z_i) - s_i||_2^2$。该Loss的目标其实就是为了压缩节点的邻居结构信息($O(|V|)$)到低维空间$z_i$。
目前广泛使用的方法是Graph Convolutional Networks（GCN）。GCN中，每个节点单独encoder，但encode的时候，会利用卷积操作来汇聚Local Neighborhoods的节点的属性信息，并叠加多层网络，形成节点的embedding表示。而卷积核参数或网络的参数是所有之间之间共享的，因此能够有效减少参数量，同时能够泛化到新的节点，只要新的节点有属性信息以及节点的Local Neighborhoods结构化信息即可。而Decoder和Loss可以使用前面提到的任意方法。关于GCN的介绍参见我的另一篇博客。
引入特定任务的监督信息。上述方法都是无监督学习目标。我们可以使用监督学习目标。例如针对一个二分类问题，将embedding经过一层MLP（$\boldsymbol{\theta}$）参数为输出一个预测值，即逻辑回归的损失函数。即：

$\mathcal{L} =\sum_{v_i \in \mathcal{V}} y_i \log(\sigma(ENC(v_i)^T\boldsymbol{\theta})) + (1-y_i)\log(1-\sigma(ENC(v_i)^T \boldsymbol{\theta}))$

从上述框架可以看出，Decoder，Loss，Similarity通常情况下是可以复用的。近年来的文章其实落脚点都主要在Encoder的改进上。如：如何融入节点的辅助信息；如何建模graph的structure；如何建模结点的local neighborhoods等。然后再通过Decoder和Loss来学习出结点的embedding。

Extension：Representative Approaches on Graphs

本节将作为上述survey的拓展。我将引入Encoder-Decoder框架，围绕现有的代表性的Graph表示学习工作，总结和抽象出不同方法中的各大组件的具体表现形式。注，读本节前，请详细阅读上述关于Encoder-Decoder框架的介绍。

DeepWalk

KDD 2014: DeepWalk: Online Learning of Social Representations

Encoder

每个节点根据id进行embedding，节点的encoder就是Embedding Lookup操作。记做：$\boldsymbol{z}_i=\text{ENC}(v_i) = \text{Embedding-Lookup}(v_i, \boldsymbol{W})$，$\boldsymbol{W} \in \mathbb{R}^{N \times k}$是所有节点的Embedding矩阵，$N$是节点数量，$k$是向量维数。

Similarity function

如何衡量原始图空间中的Ground Truth结构信息呢？DeepWalk采用的是随机游走策略。观察某个节点$v_j$出现在以$v_i$为起始节点的游走路径上的概率。$s_{\mathcal{G}}(v_i, v_j) = P_{\mathcal{G}}(v_j | v_i)$。这个概率通过在带权图上进行随机游走采样路径序列，并在序列上使用滑动窗口来构造共现节点pair来近似。$(v_i, v_j) \sim P_{\mathcal{G}}(v_j | v_i)$。

Decoder

如何衡量低维嵌入空间中的Estimated Information？DeepWalk希望上述采样到的共现节点pair的embedding越相近越好。采用的是点乘操作接softmax，即：$\text{DEC}(\boldsymbol{z_i}, \boldsymbol{z_j})=\text{softmax}(\boldsymbol{z}_i^T \boldsymbol{z}_j)$。

Loss Function

DeepWalk真正意义上的损失是交叉熵损失函数，即所有节点对上的交叉熵损失，$s_{\mathcal{G}}(v_i,v_j)$是ground truth，$\mathcal{L}(\boldsymbol{W}) = -\sum_{(v_i, v_j) \in \mathcal{R}^{|V| \times |V|}}s_{\mathcal{G}}(v_i,v_j) \log(\text{DEC}(\boldsymbol{z_i}, \boldsymbol{z_j}))$。具体实现时，无法把所有的节点对都配对，故基于采样的方式，$(v_i,v_j) \sim P_{\mathcal{G}}(v_j|v_i)$，优化目标转化为负对数似然损失函数，即：$\mathcal{L}(\boldsymbol{W})=\sum_{(v_i, v_j) \in \mathcal{D}} -\log(\text{DEC}(\boldsymbol{z}_i, \boldsymbol{z}_j))$。进一步，为了加速softmax配分函数的计算，使用层次softmax来优化。

Node2Vec

KDD 2016: node2vec: Scalable Feature Learning for Networks

和DeepWalk唯一不同点在于Similarity Function，更准确的说，是衡量哪些node pair是相似的方法不同，体现在随机游走的规则上。

Similarity Function

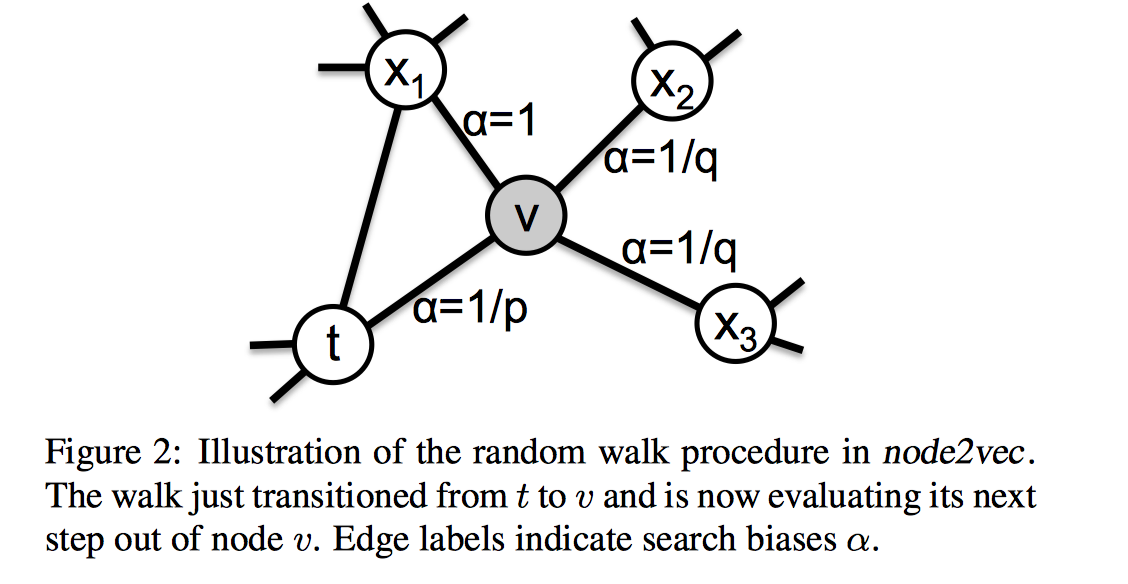
设计了有偏的游走策略来采样共现pair。考虑目前刚从节点$t$游走到某个节点$v$，准备从$v$游走到下一个节点$x$，Node2Vec会考虑$t$和$x$的关系，来约束$v$的游走规则。DeepWalk中，$P_{\mathcal{G}}(x | v) \propto w_{vx}$，即：游走概率正比于从$v$到$x$的连边权重，和怎么到达$v$的上一步$t$无关。但是在Node2Vec中，会判断下一步$x$和$t$的关系，设置一个系数$\alpha_{p,q}(x,t)$，则：

$$
P_{\mathcal{G}}(x | v) \propto \alpha_{p,q}(x,t) \cdot w_{vx}, \text{其中t是到达v的上一步节点}
$$

其中，
$$
\alpha_{p,q}(x,t) =
\begin{cases}
\frac{1}{p} & , & d_{tx}=0 \\
1 & , & d_{tx}=1 \\
\frac{1}{q} & , & d_{tx}=2
\end{cases}
$$

$d_{tx}=0$ 代表下一步$x$又回到了上一个点$t$，即同一个点。代表了回溯到上一个节点的概率。

$d_{tx}=1$代表下一步$x$和当前节点$v$同属于节点$t$的邻居节点，代表了BFS宽度优先遍历，作者认为BFS通过发现节点的局部近邻相似性能够在全图上探索出结构等价性节点。也就是说，BFS将某个节点游走限制在邻居节点，能够使得该节点获取到微观的邻居结构view。这样若在全图上存在某两个相似的、但距离较远的节点，说明这两个节点的邻居很相似，这进一步能够表明这两个节点存在结构等价性。

$d_{tx}=2$代表下一步$x$和上一步节点$t$没有直接连边，代表了DFS深度优先遍历。某个节点通过DFS游走到的节点，更多的是反映该节点在全图上的宏观view下的其邻居结构特点。即：虽然没有直接连边，但是存在潜在的相似性。这很适合用于进行社区发现。

$p$和$q$是超参数，代表了DFS和BFS之间的权衡，当都等于1时，Node2Vec退化成DeepWalk。

示意图如下：

Loss Function

和DeepWalk一样，只不过在优化softmax时，采用的是负采样方法。
$$
J_{\mathcal{G}}(\boldsymbol{z}_i)=-\log \left(\sigma(\boldsymbol{z}_i^T \boldsymbol{z}_j)\right) - \sum_{v_{j_n} \in W_j^{‘}} \log\left(\sigma(-\boldsymbol{z}_i^T \boldsymbol{z}_{j_n})\right)
$$

Line

WWW 2015: LINE: Large-scale Information Network Embedding

和Deepwalk的不同点主要体现在Similarity Function，Decoder，Loss上，即如何定义哪些node pair是在原始空间是相似的？如何定义embedding空间中node pair之间的相似性？

Similarity Function

Line定义了两种相似性node pair，一阶相似性(First-order Proximity)和二阶相似性(Second-order Proximity)。其中，

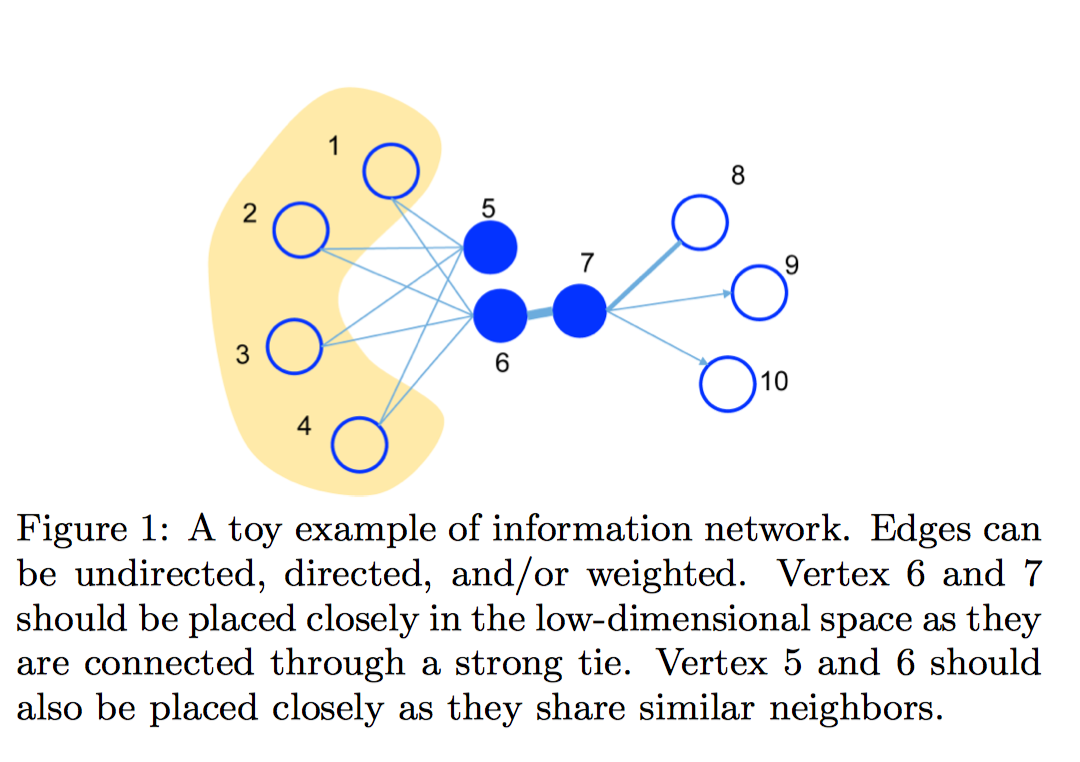
一阶相似性只针对无向图而言，是图中每一条边所对应的两个顶点之间存在相似性。即：对于每条无向边，$(i, j)$，其similarity function是$s_{\mathcal{G}}(v_i,v_j)=\hat{w}_{ij}$，其中归一化边权重$\hat{w}_{ij}=\frac{w_{ij}}{\sum_{(i,j) \in E}w_{ij}}$，即：使用所有边的权重和来归一化。如下图，6，7之间属于一阶相似性。
二阶相似性和deepwalk中类似，$s_{\mathcal{G}}(v_i, v_j) = P_{\mathcal{G}}(v_j | v_i)$。只不过Line中把每个节点的两个角色说的更清楚一些，即：target角色和context角色（deepwalk中也是有的）。context角色的意义在于，如果两个节点各自的上下文邻居很相似，那么这两个节点也相似，所以能够学习到Graph上远距离的结构相似性，如下图所示，节点5，6之间属于二阶相似性，因为5，6的上下文节点相似性（1，2，3，4）。在我看来，从生成概率角度而言，整个graph是通过若干个target节点(如社区)不断生成context节点；context节点再充当target节点，生成新的context节点而产生的。

DeepWalk中，$P_{\mathcal{G}}(v_j | v_i)$是通过随机游走+构造滑动窗口来近似，一次性能够采样到multi-hop多跳距离的节点；而在Line中，$P_{\mathcal{G}}(v_j | v_i)=\frac{w_{ij}}{d_i}$，$d_i$是节点的出度和，一次只能采样到相连接的上下文顶点$v_j$。通过context的桥梁作用(5和1相似，6和1相似，则5和6会慢慢相似；5和6相似了，因为7和6相似，则5和7可能也会慢慢相似)，在不断迭代过程中，节点’感受野’会慢慢在graph中拓展开，因此会学习到这种多跳的节点之间的相似性。所以相比于DeepWalk，Line的收敛速度可能相对比较慢(作者提到，一般迭代步数正比于$O(E)$，In practice, we ﬁnd that the number of steps used for optimization is usually proportional to the number of edges $O(|E|)$. 很多人忽视这一点，导致实际使用时性能很差)。

Decoder

对于一阶相似性，节点$(v_i, v_j)$在embedding空间的解码相似性定义为，$DEC(v_i, v_j)=\text{sigmoid}(z_i^Tz_j)=\frac{1}{1+\exp(-\boldsymbol{z}_i^T \boldsymbol{z}_j)}$，其中，$\boldsymbol{z}_i, \boldsymbol{z}_j$分别是节点$v_i,v_j$的encoder。
对于二阶相似性，节点$(v_i, v_j)$在embedding空间的解码相似性定义为，

$DEC(v_i,v_j)=p(v_j|v_i)=\text{softmax}(\boldsymbol{z}_i^T \boldsymbol{z}_j))$。如上图，$v_i$为目标结点5时，$p(\cdot |v_i)$定义了$v_i$产生上下文节点1, 2, 3, 4的概率。

Loss Function

对于一阶相似性，基于KL散度，实际上去掉常数，化简完就是交叉熵，$\mathcal{L}(\boldsymbol{W}) = -\sum_{(v_i, v_j) \in E} s_{\mathcal{G}}(v_i,v_j) \log(\text{DEC}(\boldsymbol{z_i}, \boldsymbol{z_j}))= -\sum_{(v_i, v_j) \in E} w_{ij} \log(\text{DEC}(\boldsymbol{z_i}, \boldsymbol{z_j}))$。
对于二阶相似性，基于KL散度，实际上化简完也是交叉熵。为了化简完的形式更优雅，作者引入了每个target node的重要性$\lambda_i$，得到加权的KL散度损失，即$\mathcal{L}(W)=\sum_{(i,j) \in E} \lambda_i \text {KL}(s_{\mathcal{G}}(v_i, v_j), \text{DEC}(v_i,v_j))$；使用的是节点的度$d_i$来衡量，把这几个代入并去掉常数项，很容易得到：
$$
\mathcal{L}(\boldsymbol{W}) = -\sum_{(i,j) \in E} w_{ij} \log(\text{DEC}(v_i, v_j))
$$
注意到，和DeepWalk不同的是，不管是一阶还是二阶，这里头的node pair样本对只使用每条边对应的两个顶点；而DeepWalk实际上是任意两个顶点对（全图随机游走采样，只要游走距离够长，窗口够大，任意两个节点都有可能成为相似节点对）。具体实现时，使用alias sampling，每个迭代步依$w_{ij}$分布采样节点$i$的若干个邻居$j$，优化负对数似然$ -\sum_{(i,j) \in E} \log(\text{DEC}(v_i, v_j))$。（实际上，作者实现时，是采用边采样的策略，相当于把边的权重拍扁，然后随机采边，为了更好的收敛，迭代步数要正比于边的数量（paper里头说的）；如果按照deepwalk那种方式，以点为主的话，也是可以的，只不过迭代步数要够，才好收敛，因为通常情况下，边的数量是大于点的）。

metapath2vec

KDD2017: metapath2vec: Scalable Representation Learning for Heterogeneous Networks

这篇文章将DeepWalk拓展到异构图场景。主要的改进包括：引入了meta-path based random walk，Heterogeneous Skip-Gram和Heterogeneous negative sampling。其中，meta-path based random walk属于similarity function的范畴；Heterogeneous Skip-Gram和Heterogeneous negative sampling属于Loss Function的范畴。

Similarity Function

meta-path based random walk制定一个游走规则，好处是能把节点之间的语义关系纳入到随机游走中。比如：U-I-U，I-U-I。通过该游走规则采样到的样本，可以认为是：$p(v_j |v_i, \mathcal{P})$的近似。其中，$\mathcal{P}$即为meta-path。实际上就是通过meta-path来限定转移概率分布。

注意，作者还提到，一般meta-paths都是对称的。

Loss Function

Loss形式如下：
$$
\arg \max_{\theta} \sum_{v \in V} \sum_{t \in T_V} \sum_{c_t \in N_t(v)} \log p(c_t|v;\theta)
$$
实际上就是把结点的类型纳入到损失中。$T_V$是所有的节点类型。$N_t(v)$是$v$的类型为$t$的邻居节点，即要为$v$节点采样所有类型的上下文节点$c_t, t \in T_V$。

$p$是softmax的形式的，故为了优化，作者引入了Heterogeneous Skip-Gram和Heterogeneous negative sampling。引入Skip Gram With negative sampling方法对上述Loss进行近似，即可得到：Heterogeneous Skip-Gram with negative sampling Loss：
$$
\log \sigma(\boldsymbol{z}_{c_t} \boldsymbol{z}_v) + \sum_{m=1}^M \mathbb{E}_{u^m \sim P(u)}[\log \sigma(-\boldsymbol{z}_{u^m} \cdot \boldsymbol{z}_v)]
$$
实际上和常规的Skip Gram是一样的，只不过上下文节点的类型$c_t$是基于meta-path random walk得到的。

同理，heterogeneous negative sampling也没有什么大的改动，对softmax分母的配分函数使用属于类型$t$的所有节点，而不是全部类型的节点：
$$
p(c_t|v;\theta) = \frac{\exp(\boldsymbol{z}_v^T \boldsymbol{z}_{c_t})}{\sum_{u_t \in V_t} \exp(\boldsymbol{z}_{u_t}^T\boldsymbol{z}_v)}
$$
上式重点在分母的求和项$\sum_{u_t \in V_t}$。则相应的，heterogeneous negative sampling改成使用该类型的节点上的分布$P_t(u)$即可。则对应的最终loss如下：
$$
\log \sigma(\boldsymbol{z}_{c_t} \boldsymbol{z}_v) + \sum_{m=1}^M \mathbb{E}_{u_t^m \sim P_t(u)}[\log \sigma(-\boldsymbol{z}_{u_t^m} \cdot \boldsymbol{z}_v)]
$$

Alibaba: EGES

KDD 2018: Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba

阿里KDD2018的文章，也是最早将graph embedding应用于推荐系统的工作之一。这篇文章主要是在DeepWalk基础上改进了节点的Encoder结构。

Encoder

除了节点的id的embedding之外，还融入了节点的稀疏特征的embedding。
$$
\boldsymbol{H}_v =\frac{\sum_{j=0}^n e^{a_v^{j}}\boldsymbol{w}_v^j}{\sum_{j=0}^{n}e^{a_v^{j}}}
$$
上述，$v$代表结点，$\boldsymbol{a}_{v} \in \mathbb{R}^{n+1}$，$n$是稀疏特征的数量，+1代表的是id特征(j=0是id的索引)。对于每个结点$v$，有1个$n+1$维的向量$\boldsymbol{a}_v$，向量的每个取值$a_v^j$代表第$j$个特征的权重。若结点有$N$个，则有N个$\boldsymbol{a}_{v} \in \mathbb{R}^{n+1}$向量。

$\boldsymbol{w}_v^{j}$是该结点$v$第$j$个特征的embedding，可以看出结点最终的embedding就是每个特征embedding的指数加权和，权重系数向量$\boldsymbol{a}_v$也是要学习的。上式重写一下：
$$
\boldsymbol{H}_v =\sum_{j=0}^n \frac{e^{a_v^{j}}}{\sum_{j=0}^{n}e^{a_v^{j}}} \boldsymbol{w}_v^j = \sum_{j=0}^n \text{softmax}(a_v^j) \cdot \boldsymbol{w_v^j}
$$

GraphSAGE

NIPS 2017: Inductive Representation Learning on Large Graphs

Encoder

基于邻域节点的特征汇聚。单个节点的Encoder过程如下图所示：

形式化表示为：$\boldsymbol{z}_i=\text{ENC}(v_i, \mathcal{N}(v_i))$，即：每个节点的encoder除了融入了自身节点的信息以外，还汇聚了局部的邻域节点的特征信息。汇聚的过程是个多层的网络。

初始的时候，节点使用辅助信息来表示(节点特征；节点本身的id embedding；graph上的节点拓扑结构信息，如：度)。接着对第$k$层网络，首先使用AGGREGATE函数汇聚节点$i$的邻居$\mathcal{N}(v)$的$k-1$层的表示，得到汇聚后的邻域 hidden vector，然后和自身的vector连接在一起，经过一个全连接层，再sigmoid激活，得到该节点$v_i$第$k$层的表示，可以认为该表示融入了节点$v_i$的k-hop范围内的节点的特征信息，例如：第1层的时候，融入了1-hop，即邻域节点的特征信息；同理，在第$k+1$层时，AGGREGATE函数的输入变为了第$k$层的输出表示，$k+1$层的节点表示融入了节点k+1 hop范围内的节点信息，重复该过程$K$次，就能够学习到节点在graph上K-hop的拓扑结构信息，节点的”感受野”随着迭代的进行不断扩大。注意，每次迭代完，作者还进行了一个范数归一化的操作（这个操作在层数比较大的时候应该还是必要的，还可以使用layer normalization替代）。

具体实现的时候，3~6行不需要使用所有的顶点进行更新。对于某个min-batch节点集合，只需要依次采样节点1-hop 邻居; 1-hop 邻居的邻居，即节点的2-hop 邻居；依次类推，采样到K-hop 邻居。则3~6行，只需要对这些采样到的K-hop执行操作即可，即：只要从1-hop~K-hop依次向外aggregate迭代执行即可。3~6的时间复杂度为：$O(\prod_{i=1}^K S_i)$，其中$S_i$为第$k$层采样的邻居的个数。作者在paper中使用的$K=2$，且$S1*S2 \leq 500$就能达到很好的性能。也就是说平均每个节点大概采样20个邻居。

这里头最主要的是AGGREGATE汇聚函数的设计：

Mean Aggregator: $\text{MEAN}(\boldsymbol{h}_u^{k-1}, \forall u \in \mathcal{N}(v))$， element-wise mean of the vectors.
GCN Aggregator: 4-5步合并起来，并用如下式子替换
$$
\boldsymbol{h}_v^k \leftarrow \sigma \left(\boldsymbol{W} \cdot \text{MEAN}\left({\boldsymbol{h}_v^{k-1}} \cup {\boldsymbol{h}_u^{k-1}, \forall u \in \mathcal{N}(v)}\right)\right)
$$
这个怎么理解呢？此处实际上是第三代的GCN(参考我的另一篇博客)。第三代GCN形式化：
$$
\underbrace{\boldsymbol{Z}}_{\mathbb{R}^{N \times F}} = \underbrace{\tilde{\boldsymbol{D}}^{-1/2}\tilde{\boldsymbol{W}} \tilde{\boldsymbol{D}}^{-1/2}}_{\mathbb{R}^{N \times N}} \underbrace{\boldsymbol{X}}_{\mathbb{R}^{N \times C}} \ \ \underbrace{\boldsymbol{\Theta}}_{\mathbb{R}^{C \times F}} \\\\
\boldsymbol{I_n} + \boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2} \rightarrow \tilde{\boldsymbol{D}}^{-1/2}\tilde{\boldsymbol{W}} \tilde{\boldsymbol{D}}^{-1/2}
$$

$\boldsymbol{\Theta}$类比于此处的$\boldsymbol{W}$，$X$类比于$\boldsymbol{h}$。第二个式子指的是加了skip-connection（原本W的对角元素为0），是一个renormalization trick，即：把结点自身的信息也考虑了。那么代入2式，并乘上常数$\boldsymbol{D}^{-1/2}$，可得：
$$
\boldsymbol{Z} = (\boldsymbol{I}_n + \boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2})\boldsymbol{X} \boldsymbol{\Theta} = (\boldsymbol{X}+ \boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2} \boldsymbol{X})\boldsymbol{\Theta} \\
\leftrightarrow \\
\boldsymbol{D}^{-1/2} \boldsymbol{Z} = (\boldsymbol{D}^{-1/2} \boldsymbol{X} + (\boldsymbol{D}^{-1} \boldsymbol{W}) (\boldsymbol{D}^{-1/2} \boldsymbol{X}))\boldsymbol{\Theta} \\
= (\tilde{\boldsymbol{X}} + \tilde{\boldsymbol{W}} \tilde{\boldsymbol{X}}) \boldsymbol{\Theta}
$$
$\boldsymbol{W}$是对角为0的邻接矩阵，故$\tilde{\boldsymbol{W}} \tilde{\boldsymbol{X}}$实际上获取的就是节点的邻居的特征，因此，实际上也是对节点的邻居做了汇聚操作，再加上自身的节点特征（通过skip-connection实现的，和concat是异曲同工！）。故，GCN Aggregator 和 Mean Aggregator+Concat实际上异曲同工，二者是线性近似的关系。
LSTM aggregator: 直接对邻域节点随机扰动permutation，然后将扰动后的序列使用LSTM来聚合。感觉有点简单粗暴了。
Pooling aggregator：
$$
\text{AGGREGATE}_k^{pool}=\max({\sigma(\boldsymbol{W}_{pool}\boldsymbol{h}_{u_i}^k + \boldsymbol{b}), \forall u_i \in \mathcal{N}(v)})
$$
即：每个邻居节点的表示先经过一个MLP，然后进行sigmoid激活；最后应用element-wise max pooling策略，此处的max pooling，作者提到用mean pooling也是可以的。内部的MLP也可以改成多层的MLP。

另外，similarity function作者采用的相似性函数和deepwalk一样，$s_{\mathcal{G}}(v_i, v_j) = P_{\mathcal{G}}(v_j | v_i)$，并通过基于graph的随机游走来构造共现对来近似（原paper: where $v$ is a node that co-occurs near $u$ on ﬁxed-length random walk）。为了佐证这点，笔者特地读了原作者实现的代码，其中：

# link: https://github.com/williamleif/GraphSAGE/blob/a0fdef95dca7b456dab01cb35034717c8b6dd017/graphsage/unsupervised_train.py#L143

context_pairs = train_data[3] if FLAGS.random_context else None
placeholders = construct_placeholders()
minibatch = EdgeMinibatchIterator(G, 
                                  id_map,
                                  placeholders, batch_size=FLAGS.batch_size,
                                  max_degree=FLAGS.max_degree, 
                                  num_neg_samples=FLAGS.neg_sample_size,
                                  context_pairs = context_pairs)
# 可以看出，如果FLAGS.random_context为True，则使用random walk得到的上下文节点对构造正样本对；
# 其中train_data[3]即为walks构造得到的上下文边。
# 如果FLAGS.random_context为False, 则直接使用连边来构造正样本对
# 默认取值为True，故默认用的是random walk。

除此之外，Loss Function中，无监督的损失函数和Node2Vec一样，采用的是skip-gram with negative sampling。Decoder和DeepWalk/Node2Vec也一样。

GATs

ICLR 2018：Graph Attention Networks

ICLR 2018的文章，在GraphSAGE基础上，引入了self-attention机制对aggregator进行了改进。

Encoder

基于邻域节点的特征汇聚。只不过引入了self-attention机制，每个节点attend到自身的邻域节点上。不同于GraphSAGE采用Mean/Pooling Aggregator，GATs采用了基于self-attention机制的Aggregator。也就是说，把目标节点的表示和邻域节点的表示通过一个attention网络，计算注意力值，再依据该注意力值来aggregate邻域节点。对于节点$i$及其邻域节点$j$。我们要计算$i$节点attend到$j$的注意力值，attention score计算如下：

先对$i$和$j$的node feature分别做一个线性变换 (即multi-head attention的特例，1-head attention)，$\boldsymbol{W} \boldsymbol{h}_i$
再把变换后的表示送到attention网络并进行softmax得到注意力值，$\alpha_{ij} = \text{softmax}(\text{attention}(\boldsymbol{W} \boldsymbol{h}_i, \boldsymbol{W} \boldsymbol{h}_j))=\text{softmax}(e_{ij})$，这个attention网络就可以随便设计和尝试了。作者使用的是：
$$
e_{ij}=\text{LeakyReLU}(\boldsymbol{a}[\boldsymbol{W}\boldsymbol{h}_i ,\boldsymbol{W}\boldsymbol{h_j}])
$$
即：二者Concat到一起后，经过一个线性变换$\boldsymbol{a}$ (attention网络的参数)，再LeakyReLU激活。另外，对于节点$i$和自身的attention score，作者提到直接代入$j=i$即可。

则Aggregator直接依注意力值对线性变换后的vector加权并激活即可：
$$
\boldsymbol{h}^{\prime}_i = \sigma(\sum_{j \in \mathcal{N}_i}\alpha_{ij} \boldsymbol{W} \boldsymbol{h}_j)
$$
另外，作者提到，可以采用multi-head attention来拓展，即：attention score计算的第一步中，将node feature变换到不同的语义子空间，再进行attention score计算并aggregate。每个head输出一个$\boldsymbol{h}_i^{\prime}$，将所有的输出concat到一起；或者做mean pooling，作为节点的最终表示。

示意图如下：

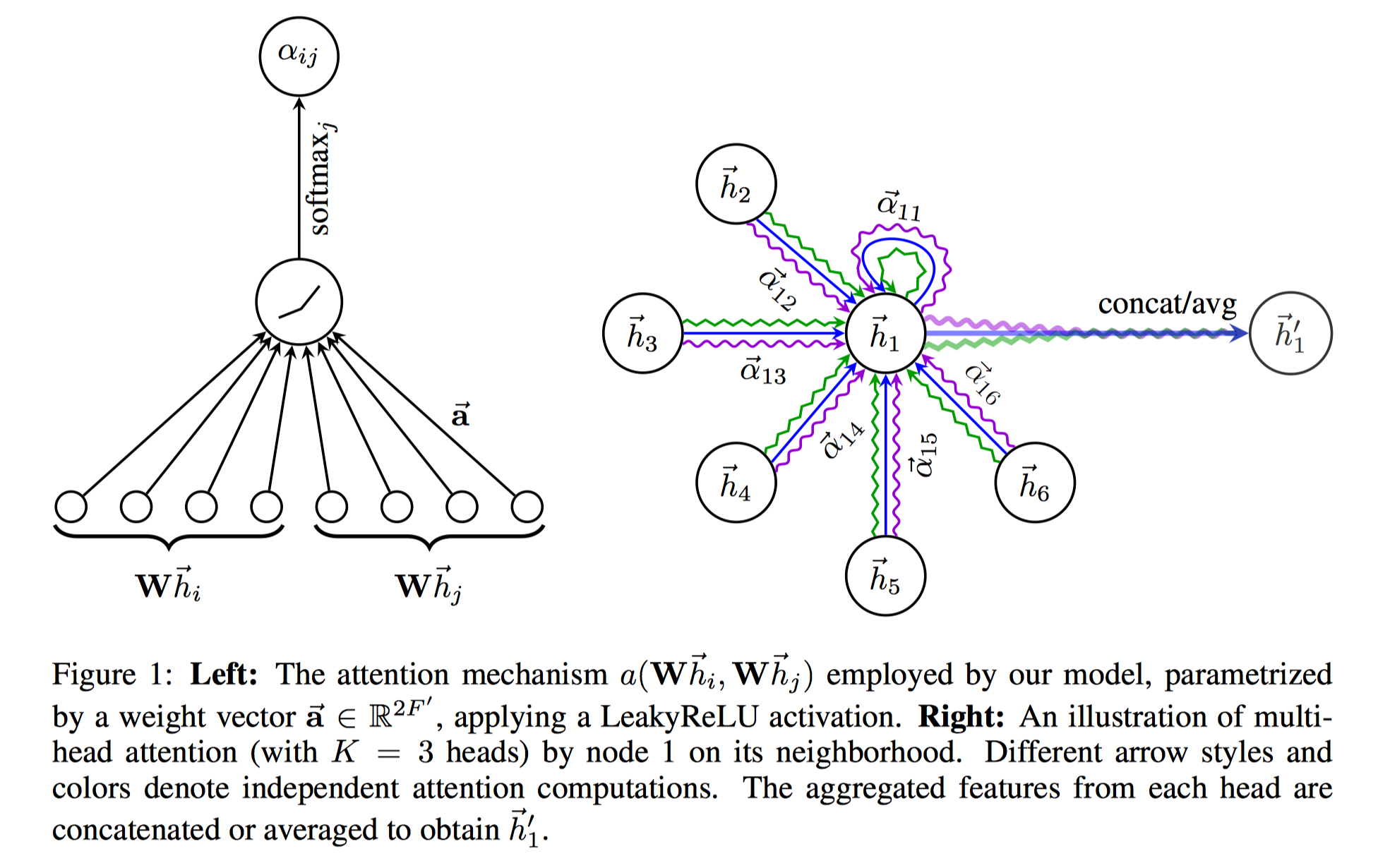
上述描述的是单层的GAT。实际上，可以像GraphSAGE那样，设置多层。作者在实验中，采取的是2层以及3层的GAT。

PinSAGE

KDD2018: Graph Convolutional Neural Networks for Web-Scale Recommender Systems

Encoder

encoder结构非常简单，伪代码如下：

主要步骤和GraphSAGE几乎是一样的。$\gamma$就是Aggregation Function。作者提到，步骤2中的concat操作比average操作效果要好很多；步骤3中的归一化操作使得训练更稳定，且对后面基于embedding的相似性搜索更加高效。实际上，作者采用的$\gamma$是weighted mean pooling aggregator（important pooling aggregator）。其中，weight根据下面介绍的基于重要性的领域节点采样方法。

关键点在于，

基于重要性的邻域节点的采样：Importance-based neighborhoods.

传统的方法从目标结点$u$开始采样K-hop的邻居。作者采用了从$u$起始的随机游走的方式，并计算随机游走过程中每一个路径上的节点的L1-normalized visit count；则邻域节点定义为：最大的Top $T$ L1-normlized visit count。则每个邻域节点的weight也根据L1-normalized visit count来计算。作者称这种方法为important pooling。

层叠式卷积层：Stacking convolutions

实际上指的就是使用多层的卷积操作，前一层的结果作为下一层的输入。跟GraphSAGE中也是一样的，只不过作者换了个名字。

作者接着将卷积得到的结果通过2个全连接层得到最终节点的embedding。

Loss Function

作者采用了最大间隔损失函数（类似pairwise SVM Loss)。对某个正样本对$(q, i)$，其损失为：
$$
J_{\mathcal{G}}(\boldsymbol{z}_q \boldsymbol{z}_i) = \mathbb{E}_{n_k \sim P_n(q)}\max \{0, \boldsymbol{z}_q \cdot \boldsymbol{z}_{n_k} - \boldsymbol{z}_q \boldsymbol{z}_i + \Delta \}
$$
其中，$n_k$是采样的负样本，即，和$q$不相关的样本。$\Delta$是间隔参数，例如一般设置为1。

多说几句，个人认为这个文章的亮点主要在工程实现，作者提到了很多部署模型的细节，例如多GPU训练；生产消费者模式来产生训练样本等。尤其是生产消费者模式这个值得借鉴：由于graph图数据和节点的特征数据非常大，只能存储在CPU中，训练的时候如果让TF把数据从CPU搬到GPU来计算的话，代价是非常庞大的。作者的思路是，使用re-indexing技术，构造包括节点以及其邻域的子图，并把其纳入到mini-batch数据产生器中，使得子图在每次mini-batch 迭代开始前就已经送到GPU中了。个人认为就是利用了TF自带的喂数据的接口，并封装了一下generator。CPU中提取节点特征，re-indexing，负采样产生训练样本的操作可以认为是生产者；GPU中消费数据来训练样本可以认为是消费者。

对于负采样，作者为每个子图一次性采样了500个共享的负样本，可以有效的减少训练时间。如果每个节点都采样本的话，训练的时候，需要为每个负样本都计算embedding，非常耗时（感同身受）。

对于负样本采样个数，作者也有比较深入的讨论（非常值得学习）。Pinterest需要从20亿多个Item中，为每个Item找到最相关的1000个Item（1：2,000,000，相当于200万个Item中得找到1个相关Item）；如果使用均匀分布随机采样500个负样本的话，相当于从500个Item中找到1个相关Item，显然是不够的。为了解决这个问题，作者引入了hard negative samples的概念，除了负采样easy negative samples，作者还采样了hard negative samples。用的是相对于正样本$q$，Personalized PageRank取值最高的若干负样本。具体训练时，交替执行，1轮不用hard samples，1轮使用hard samples（作者称这种方式为：curriculum training scheme）。

最后，作者还提到对于重复计算embedding的问题。每个节点的邻居可能存在交叉，即：某个节点是多个其他目标结点的邻居，此时这个节点只需要计算一次embedding即可。作者采用了Map-Reduce架构来防止重复的计算问题。

GATNE

KDD 2019: Representation Learning for Attributed Multiplex Heterogeneous Network

作者在这篇文章中想要解决的是一种多类型节点，多类型连边关系的异构图网络的表示学习。这种网络称作AMHEN（Attributed Multiplex Heterogeneous Network），可以翻译做复合异构属性网络。

Heterogeneous Network: 多种类型节点/边的异构网络。
Attributed：节点的属性。
Multiplex：节点与节点之间的连边关系可以是多种。例如：电商邻域的user-item的交互关系包括了：click, conversion, add-to-cart, add-to-preference等。

作者提出了一种叫做GATNE（General Attributed Multiplex HeTerogeneous Network Embedding）的模型，能够建模丰富的属性信息，并从不同类型的节点中捕捉复合拓扑结构（capture both rich attributed information and to utilize multiplex topological structures from different node types）。

看到这里，我们对作者的思路其实已经略知一二了。作者主要的创新点在于把节点之间多种多样的连边关系融入到节点的Encoder中。Multiplex在其他文章可能叫做Multi-View，即多视图。直觉上而言，节点之间的连边关系的层次是不同的，例如U-I交互中的click和conversion关系，显然是不等的。把这种交互关系的层次区分开，确实值得借鉴。下面就要看作何如何设计Encoder架构来建模多种连边关系，区分开不同level的interaction关系，并统一到Encoder中。

Encoder

首先给出AMHEN的形式化表述：

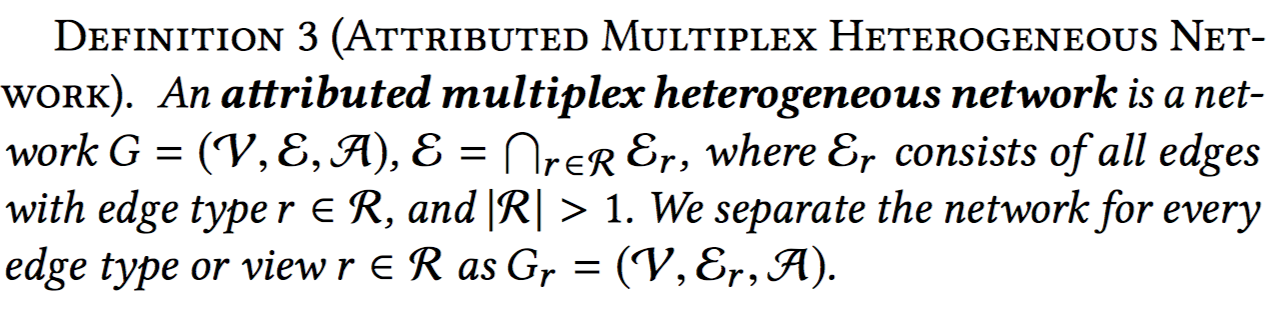
作者实际上仍然是把Multi-View Graph拆分开为多个1-View Sub-Graph。

Step 1: 首先对每个节点在每个View Graph下各自进行Encoder，记做：$\boldsymbol{u}_{i,r}$，即节点$i$在View $r$下的Embedding (作者称作Edge Embedding，但实际上是更准确的是，在某种edge-view下的Node Embedding)。对于$\boldsymbol{u}_{i,r}$，作者采用了GraphSAGE的方法，基于邻域节点的特征汇聚。对于第$k$层的edge embedding：

$$
\boldsymbol{u}_{i,r}^k=\text{aggregator}(\{\boldsymbol{u_{j,r}}^{k-1}, \forall v_j \in \mathcal{N}_{i,r} \})
$$

即：使用r-view sub-graph下，$i$的邻域节点汇聚得到$u_{i,r}$。对于transductive learning，初始化的$\boldsymbol{u}_{i,r}^0$随机初始化（也就是每个节点在每种view下都有唯一的 id embedding）。最终$\boldsymbol{u}_{i,r}^K$作为$\boldsymbol{u}_{i,r}$。此处，只用到r-view下，邻域节点的edge embeddings，未用到自身的edge embedding。aggregator可以使用mean pooling或者max pooling。

Step 2: 接着，把每个view下得到的edge embedding，concat到一起，

$$
\boldsymbol{U}_i = (\boldsymbol{u}_{i,1}, \boldsymbol{u}_{i,2},…,\boldsymbol{u}_{i,m})
$$

$\boldsymbol{U_i} \in \mathbb{R}^{s \times m}$矩阵，$s$是$\boldsymbol{u}_{i,r}$的维度数，$m$是连边类型的数量。

Step 3: 接着，作者会对$\boldsymbol{U}_i$使用self-attention网络。目标是：某个节点$i$在edge type $r$下的overall embedding，融入$i$在所有edge type的关联关系，再依据该关联关系的强度对$\boldsymbol{U}_i$做一个线性组合，得到r-view下的，节点的overall embedding。

为此，引入了self-attention网络，可以把$\boldsymbol{U}_i$类比作word序列，每个word都要focus到句子的每个word上。同理，每个edge embedding都要focus到所有的edge embeddings上。对于某个edge type $r$，首先计算focus到所有edge embedding上的权重向量：
$$
\boldsymbol{a}_{i,r}=\text{softmax}(\boldsymbol{w}_r^T \text{tanh}(\boldsymbol{W}_r \boldsymbol{U}_i))^T
$$
其中，$\boldsymbol{a}_{i,r} \in \mathbb{R}^m$，$W_r \in \mathbb{R}^{d_a \times s}, \boldsymbol{w}_r \in \mathbb{R}^{d_a}$。衡量了r-view下，节点$i$和所有edge emebddings的关联程度。怎么从直觉上，或者从attention的范式上（Query, Key, Value）理解该self-attention网络呢？

$\boldsymbol{W}_r, \boldsymbol{w}_r$是r-view specific权重参数，可以认为是Query，$\boldsymbol{U}_i$是all-view下节点$i$的edge embeddings，可以认为是Key，即：探讨r-view和$i$的all-view的关联关系（Query和Key的关联关系），得到的就是$i$的r-view和all-view的关联关系。

再依据关联关系对Value ($\boldsymbol{M}_r^T \boldsymbol{U}_i$) 做聚合得到最终的节点$i$在edge type $r$下的overall embedding。
$$
\boldsymbol{v_{i,r}}=\boldsymbol{b_i} + \alpha_r (\boldsymbol{M_r}^T \boldsymbol{U}_i) \boldsymbol{a}_{i,r}
$$
$b_i$是节点的base embedding(node-specific，所有view共享)；$\boldsymbol{M}_r^T \boldsymbol{U}_i$其实就是对Key $\boldsymbol{U}_i$做了个r-view specific transformation，最简单的情况下，$\boldsymbol{U}_i$既是Key，又是Value，此处额外做了个线性变换。然后基于self-attention向量$\boldsymbol{a}_{i,r}$做加权。$\alpha_r$是个可学习的常量系数，衡量了相比于base embedding，edge embeddings对overall embedding的重要性。

上述是transductive learning，为了实现inductive learning，只需要把$\boldsymbol{b}_i=h_z(\boldsymbol{x}_i)$ , 且$\boldsymbol{u}_{i,r}^0=g_{z,r}(\boldsymbol{x}_i)$, $\boldsymbol{x_i}$是节点的attribute向量，$z$是节点的类型，$h_z$，$g_{z,r}$是映射函数，如线性变换。除此之外，作者还加了一项关于节点本身attribute关于节点类型的线性变换项，最终形成如下的embedding：
$$
\boldsymbol{v_{i,r}}=h_z(\boldsymbol{x}_i) + \alpha_r (\boldsymbol{M_r}^T \boldsymbol{U}_i) \boldsymbol{a}_{i,r} + \beta_r \boldsymbol{D}_z^T \boldsymbol{x}_i
$$
作者为每个节点学习了$m$种embedding，$\boldsymbol{v}_{i, 1},…,\boldsymbol{v}_{i, m}$，并没有把$m$种aggregate到一起。说明在Similarity Function或者Loss Function上有一定的设计。

Similarity Function

作者使用的和metapath2vec方法差不多的similarity function，由于是异构网络，作者引入了meta-based random walk来得到similarity function，$p(v_j |v_i , \mathcal{T})$。对于某个r-view sub-Graph $\mathcal{G}_r = (\mathcal{V}, \mathcal{E}_r , \mathcal{A})$, meta-path scheme $\mathcal{T}: \mathcal{V}_1 \rightarrow \mathcal{V}_2 \rightarrow … \rightarrow \mathcal{V}_t \rightarrow … \rightarrow \mathcal{V}_l$，其中$l$是meta-path scheme的长度。每个sub-graph分别按照这种方式采样训练样本。作者采用的meta-path其实就是U-I-U, I-U-I。

Loss Function

作者采取的损失为Skip Gram with negative sampling。对于某个node pair $(v_i,v_j)$，损失为：
$$
E = − \log \sigma(\boldsymbol{c}_j^T \cdot \boldsymbol{v}_{i,r}) − \sum_{l=1}^L \mathbb{E}_{v_k \sim P_t(v)}[\log \sigma(-\boldsymbol{c}_k^T \boldsymbol{v}_{i,r})]
$$
会根据该node pair的连边类型$r$，选择对应的$\boldsymbol{v}_{i,r}$。这样相当于每个节点可以学到$m$种embedding。

遗憾的是，作者没有对$m$种embedding做一个aggregator。看了下实验，可能对于node-node之间多种的interaction关系进行链接预测时，使用对应的$\boldsymbol{v}_{i,r}$。但是实际进行推荐的时候，是不是聚合一下得到唯一的embedding更好呢？

Summary

本文介绍了一种Encoder-Decoder框架，用于抽象和组织关于Representation Learning on Graph的方法。对于发现方法中的核心思想和核心组成部分有非常好的辅助作用。同时，该框架可以用于指导关于图表示学习的编程实践。据我所知，Alibaba开源的图表示学习框架 Euler 中，核心模型层的代码就是使用该Enocder-Decoder结构来组织的。这是一个非常好的实践，对于定义Encoder和Decoder的定制非常方便，笔者一直在用。后续有机会会分享一下关于Euler的实践经验。