本文主要介绍主成分分析算法(Principal Components Analysis,PCA)。该算法尝试搜寻数据所处的子空间,只需计算特征向量就可以进行降维。本文将尝试解释为什么通过特征向量计算能够实现降维。同时将介绍使用奇异值分解(SVD)方法来实现PCA求解。
基于股评的情感分析和股市投资策略研究
本次双学位论文的题目是基于股评的情感分析和投资策略研究。阐述围绕四个方面展开,研究背景和内容、构建情感分析模型、构建时间序列预测模型以及总结展望。
Advice for applying Machine Learning(2)
本文对Advice for applying Machine Learning一文中提到的算法诊断等理论方法进行实践,使用Python工具,具体包括数据的可视化(data visualizing)、模型选择(choosing a machine learning method suitable for the problem at hand)、过拟合和欠拟合识别和处理(identifying and dealing with over and underfitting)、大数据集处理(dealing with large datasets)以及不同代价函数(pros and cons of different loss functions)优缺点等。
Advice for applying Machine Learning
本文对Ng提到的关于机器学习应用实践上的建议进行整理总结。主要内容包括:诊断(Diagnostics for debugging learning algorithms)、误差分析(error enalysis)、销蚀分析(ablative analysis)、过早优化(premature optimization)。并结合“自动驾驶直升机”应用探讨如何对存在问题进行诊断。
Learning Theory
本文与前面不同,主要内容不是算法,而是机器学习的另一部分内容——学习理论。主要包括偏差/方差(Bias/Variance)、经验风险最小化(Empirical Risk Minimization,ERM)、联合界(Union bound)、一致收敛(Uniform Convergence)。
偏差/方差权衡
回顾一下,当我们讨论线性回归时,我们尝试过使用简单的线性方法,如\(y=\theta_0 + \theta_1 x\),也尝试使用更复杂的模型,如多项式\(y=\theta_0+\theta_1 x+…+\theta_5 x^5\)。观察下图: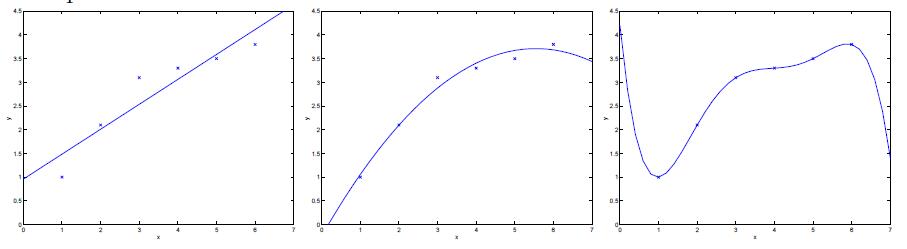
以上述回归问题为例,机器学习的目标是从训练集中得到一个模型,使之能对测试集进行分类。这里训练集和测试集都是分布\(\mathcal{D}\)的样本。机器学习的关注点在于模型在测试集上的分类效果,这也称作泛化能力(generalization ability)。如上图,最左边的图用一个线性模型进行拟合,显然即使拥有很多的训练集,该模型在测试集上进行预测的话,仍然存在着很大的误差,这种情况称为欠拟合,对应着高偏差。对于最右边的图,用一个高阶(五阶)去拟合,从数据中得到的模型结构很可能碰巧是该训练集特有的,即尽管五次多项式模型对训练集的拟合不错,但并非是一个好的模型,因为对于训练集以外的数据,该模型不一定能很好得进行预测,即泛化能力不够好,因此仍然存在着很大的泛化误差,这种情况称作过拟合,对应高方差。
在机器学习中,对偏差和方差的权衡是学习理论重点解决的问题。如果我们的模型太过于简单,只有少量的参数要学习,那么就可能存在高偏差(large bias but small variance)。如果我们的模型太过于复杂,拥有大量的参数,那么就可能存在高方差(large variance but small bias)。在上面的例子中,训练一个二次型的模型(对应中间那幅图),比训练一个过于简单的一次型模型或过于复杂的五次型模型都好。
SVM支持向量机
本文将介绍SVM(Support Vector Machine)学习算法。SVM是现有的最强大的监督学习算法。我们首先讨论什么是间隔以及使用最大间隔来分类数据的思想。接着讨论最优间隔分类器,这里面会涉及拉格朗日对偶问题。我们也会讨论关于核方法以及如何有效地应用核方法到高维特征空间。最后我们会讨论SMO算法,它是SVM的一种实现方法。
间隔的直观理解
要理解支持向量机,首先必须先了解间隔以及关于预测置信度的概念。考虑一下逻辑回归,模型是\(h_\theta(x)=g(\theta^Tx)\),当且仅当\(h_\theta(x) \geq 0.5\),也即\(\theta^Tx \geq 0\)时,我们预测结果为1。考虑一个正例样本,显然\(\theta^Tx\)的值越大,\(h_\theta(x)=p(y=1|x;w;b)\)的值也越大,则预测样本label为1的置信程度也越高。更正式的,当\(\theta^Tx \gg 0\)时,可以认为我们的预测样本label为1的置信程度很高,同样,当\(\theta^Tx \ll 0\)时,可以认为我们的预测样本label为0的置信程度很高。给定一个训练集,如果我们能够在标签为1的样本中,找到合适的\(\theta\),使得\(\theta^Tx^{(i)} \gg 0\),那么这样拟合的效果就很好。同样,在标签为0的样本中,找到合适的\(\theta\),使得\(\theta^Tx^{(i)} \ll 0\)。这样的拟合效果能够体现出分类器对于样本分类的置信程度很高。后面我们会使用函数间隔来形式化该思想。
生成算法
这篇笔记主要针对斯坦福ML公开课的第五个视频,主要内容包括生成学习算法(generate learning algorithm)、高斯判别分析(Gaussian Discriminant Analysis)、朴素贝叶斯(Navie Bayes)、拉普拉斯平滑(Laplace Smoothing)。
生成学习算法概述
到目前为止,我们学习的方法主要是直接对问题进行求解,比如二分类问题中的感知机算法和逻辑回归算法,都是在解空间中寻找一条直线从而把两种类别的样例分开,对于新的样例只要判断在直线的哪一侧即可,这种截至对问题求解的方法可以称作判别学习方法(discriminative learning algorithm)。判别学习方法的任务是训练如下模型:
$$p(y|x;\theta)$$
Python实现时间序列分析
前面花了两章篇幅介绍了时间序列模型的数学基础。 ARIMA时间序列模型(一)和ARIMA时间序列模型(二) 。本文重点介绍使用python开源库进行时间序列模型实践。
基本概念
回顾一下自回归移动平均模型ARMA,它主要由两部分组成:AR代表p阶自回归过程,MA代表q阶移动平均过程,形式如下:
$$Z_t=\theta_0+\phi_1 Z_{t-1}+\phi_2 Z_{t-2}+…+\phi_p Z_{t-p} \\\\
+a_t-\theta_1a_{t-1}-\theta_2a_{t-2}-…-\theta_qa_{t-q}$$
为了方便,我们重写以上等式为:
$$\phi(B)Z_t=\theta_0+\theta(B)a_t \\\\
其中,\phi(x)和\theta(x)分别是AR模型和MA模型的的特征多项式$$
$$\phi(x)=1-\phi_1x-\phi_2x^2-…-\phi_px^p$$
$$\theta(x)=1-\theta_1x-\theta_2x^2-…-\theta_px^q$$
根据前两篇的分析,我们总结ARMA模型的性质如下: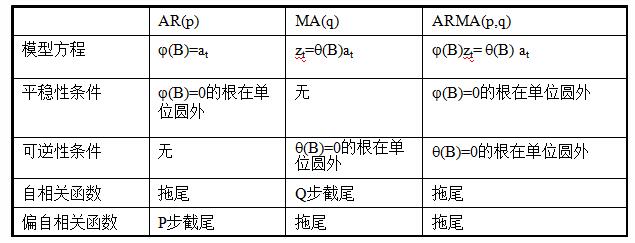
ARIMA时间序列模型(二)
前面我们介绍了时间序列模型的概念、数学基础等。本文将接着介绍时间序列模型的更多理论性质,包括一般线性过程(general linear process),自回归模型AR(the autoregressive model),移动平均模型MA(the moving average)以及ARMA模型。
一般线性过程
定义:
- 时间序列\({Z_t}\)是线性(linear)的,当且仅当\(Z_t\)的值是白噪声系列的线性函数。
- 时间序列\({Z_t}\)是有因果的(causal),当且仅当\(Z_t\)的值只受到目前为止的信息影响,换句话说\(Z_t\)是独立于未来信息\(a_s\)的,s>t
- 时间序列模型通常是由白噪声驱动的,即\({a_t}\), 时间序列是\({a_t}\)的函数。随机变量\(a_t\)可以被时刻t的信息所解释。白噪声通常叫做新息序列(innovation sequence)或信息序列(information sequence).
因此,一个线性的、有因果的、平稳的时间序列也被称作一般线性过程(a general linear process)。
一般线性过程具有如下形式:
$$Z_t=\mu+\sum_{j=0}^{\infty}\psi_j a_{t-j}=\mu+\psi_0a_t+\psi_1a_{t-1}+\psi_2a_{t-2} \\\\
其中,{a_t} \sim WN(0,\sigma_a^2) \ and \ \sigma_a^2\sum_{j=0}^{\infty}\psi_j^2<\infty$$
不失一般性,我们可以设\(\psi_0=1\)
ARIMA时间序列模型(一)
基本概念
时间序列是什么?
定义:时间序列数据是按时间排序的观察序列,是目标在不同时间点下的一系列观察值。
所有的时间观察序列数据可以被标记为:\(z_1,z_2,…,z_T\) , 可以当作T个随机变量的一个实例:$$(Z_1,Z_2,..,Z_T)$$
进一步定义:时间序列是一系列按照时间排序的随机变量。通常定义为双无穷随机变量序列。标记为:\({Z_t,t \in \mathbb{Z}}\), 或者简记为:\({Z_t}\) 。时间序列是离散时间下的随机过程。
回顾线性模型,响应变量Y和多个因变量X,线性模型表示为:$$Y_i=\beta_0+\beta_1X_i+\varepsilon_i$$
因变量X的信息是已知的,我们希望对响应变量Y做出推断。
在时间序列分析中,我们提出如下模型:$$Y_t=\beta_o+\beta_1Y_{t-1}+\varepsilon_t$$
在时间序列中,已知的信息包括:
- 时间下标t
- 过去的信息
两个典型的时间序列模型如下:
$$Z_t=a+bt+\varepsilon_t$$
and
$$Z_t=\theta_0+\phi Z_{t-1}+\varepsilon_t$$
它们分别对应于确定性模型和随机模型,本文将讨论后者。